Cykeldiagram (algebra)

I gruppteorin , ett underfält av abstrakt algebra , illustrerar en gruppcykelgraf de olika cyklerna i en grupp och är särskilt användbar för att visualisera strukturen hos små ändliga grupper .

En cykel är mängden potenser av ett givet gruppelement a , där a ⁿ , den n -te potensen av ett element a definieras som produkten av a multiplicerat med sig själv n gånger. Elementet a sägs generera cykeln. I en finit grupp måste någon potens av a som inte är noll vara gruppidentiteten , e ; den lägsta sådan makten är ordning , antalet distinkta element i den. I en cykelgraf representeras cykeln som en polygon, där hörnen representerar gruppelementen och de anslutande linjerna indikerar att alla element i den polygonen är medlemmar av samma cykel.

Cyklar

Cykler kan överlappa varandra, eller så kan de inte ha något gemensamt element förutom identiteten. Cykeldiagrammet visar varje intressant cykel som en polygon.

Om a genererar en cykel av ordning 6 (eller kortare sagt, har ordning 6), då är a ⁶ = e . Då är uppsättningen potenser av a ² , { a ² , a ⁴ , e } en cykel, men detta är egentligen ingen ny information. På samma sätt en ⁵ :a samma cykel som en själv.

Så det är bara de primitiva cyklerna som behöver beaktas, nämligen de som inte är delmängder av en annan cykel. Var och en av dessa genereras av något primitivt element , en . Ta en poäng för varje element i den ursprungliga gruppen. För varje primitivt element, koppla e till a , a till a ² , ..., a ^{n −1} till a ⁿ , etc., tills e nås. Resultatet är cykeldiagrammet.

När a ² = e har a ordning 2 (är en involution ), och är kopplad till e med två kanter. Förutom när avsikten är att betona cykelns två kanter, ritas den vanligtvis som en enda linje mellan de två elementen.

Egenskaper

Dih ₄ kalejdoskop med röd spegel och 4-faldiga rotationsgeneratorer	Cykeldiagram för dihedrisk grupp Dih ₄ .

Som ett exempel på en gruppcykelgraf, betrakta den dihedriska gruppen Dih ₄ . Multiplikationstabellen för denna grupp visas till vänster, och cykeldiagrammet visas till höger med e som anger identitetselementet.

^o	e	b	a	en ²	en ³	ab	a ² b	a ³ b
e	e	b	a	en ²	en ³	ab	a ² b	a ³ b
b	b	e	a ³ b	a ² b	ab	en ³	en ²	a
a	a	ab	en ²	en ³	e	a ² b	a ³ b	b
en ²	en ²	a ² b	en ³	e	a	a ³ b	b	ab
en ³	en ³	a ³ b	e	a	en ²	b	ab	a ² b
ab	ab	a	b	a ³ b	a ² b	e	en ³	en ²
a ² b	a ² b	en ²	ab	b	a ³ b	a	e	en ³
a ³ b	a ³ b	en ³	a ² b	ab	b	en ²	a	e

Lägg märke till cykeln { e , a , a ² , a ³ } i multiplikationstabellen, med a ⁴ = e . Inversen a ⁻¹ = a ³ är också en generator av denna cykel: ( a ³ ) ² = a ² , ( a ³ ) ³ = a , och ( a ³ ) ⁴ = e . På liknande sätt har vilken cykel som helst i vilken grupp som helst minst två generatorer och kan passeras i båda riktningarna. ges antalet generatorer av en cykel med n element av Euler φ-funktionen för n , och vilken som helst av dessa generatorer kan skrivas som den första noden i cykeln (bredvid identiteten e ); eller mer vanligt att noderna lämnas omarkerade. Två distinkta cykler kan inte skära varandra i en generator.

Cykeldiagram för quaterniongruppen Q ₈ .

Cykler som innehåller ett icke-primtal av element har cykliska undergrupper som inte visas i grafen. För gruppen Dih ₄ ovan skulle vi kunna dra en linje mellan a ² och e eftersom ( a ² ) ² = e , men eftersom en ² är en del av en större cykel är detta inte en kant på cykelgrafen.

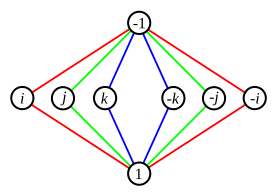
Det kan finnas tvetydigheter när två cykler delar ett icke-identitetselement. Till exempel har 8-elements quaternion-gruppen en cykelgraf som visas till höger. Vart och ett av elementen i mittenraden, multiplicerat med sig självt, ger −1 (där 1 är identitetselementet). I det här fallet kan vi använda olika färger för att hålla reda på cyklerna, även om symmetriöverväganden kommer att fungera också.

Som noterats tidigare representeras de två kanterna av en 2-elementscykel typiskt som en enda linje.

Inversen av ett element är noden symmetrisk till det i dess cykel, med avseende på reflektionen som fixerar identiteten.

Historia

Cykelgrafer undersöktes av talteoretikern Daniel Shanks i början av 1950-talet som ett verktyg för att studera multiplikativa grupper av restklasser . Shanks publicerade idén först i 1962 års första upplaga av sin bok Solved and Unsolved Problems in Number Theory . I boken undersöker Shanks vilka grupper som har isomorfa cykelgrafer och när en cykelgraf är plan . I 1978 års andra upplaga reflekterar Shanks över sin forskning om klassgrupper och utvecklingen av baby-step giant-step- metoden:

Cykeldiagrammen har visat sig vara användbara när man arbetar med ändliga Abelska grupper; och jag har använt dem ofta för att hitta runt en invecklad struktur [77, sid. 852], för att erhålla en önskad multiplikativ relation [78, sid. 426], eller för att isolera någon eftersökt undergrupp [79].

Cykeldiagram används som ett pedagogiskt verktyg i Nathan Carters 2009 inledande lärobok Visual Group Theory .

Grafkarakteristika för särskilda gruppfamiljer

Vissa grupptyper ger typiska grafer:

Cykliska grupper Z _n , ordning n , är en enskild cykel som helt enkelt är grafisk som en n -sidig polygon med elementen vid hörnen:

Z ₁	Z ₂ = Dih ₁	Z ₃	Z ₄	Z ₅	Z6 = _Z3 × _Z2_{_}	Z ₇	Z ₈


Z ₉	Z ₁₀ = Z ₅ × Z ₂	Z ₁₁	Z ₁₂ = Z ₄ × Z ₃	Z ₁₃	Z ₁₄ = Z ₇ × Z ₂	Z ₁₅ = Z ₅ × Z ₃	Z ₁₆

Z ₁₇	Z ₁₈ = Z ₉ × Z ₂	Z ₁₉	Z ₂₀ = Z ₅ × Z ₄	Z ₂₁ = Z ₇ × Z ₃	Z ₂₂ = Z ₁₁ × Z ₂	Z ₂₃	Z ₂₄ = Z ₈ × Z ₃

Z ₂	Z ₂² = Dih ₂	Z ₂³ = Dih ₂ × Dih ₁	Z ₂⁴ = Dih ₂²

När n är ett primtal kommer grupper av formen (Z _n ) ^m att ha ( n ^m − 1)/( n − 1) n -elementcykler som delar identitetselementet:

Z ₂² = Dih ₂	Z ₂³ = Dih ₂ × Dih ₁	Z ₂⁴ = Dih ₂²	Z ₃²

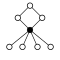
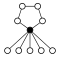
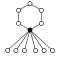
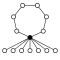
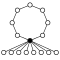
Dihedriska grupper Dih _n , ordning 2 n består av en n -elementcykel och n 2-elementcykler:

Dih ₁ = Z ₂	Dih ₂ = Z ₂²	Dih ₃ = S ₃	Dih ₄	Dih ₅	Dih ₆ = Dih ₃ × Z ₂	Dih ₇	Dih ₈	Dih ₉	Dih ₁₀ = Dih ₅ × Z ₂

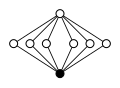
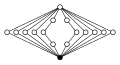
Dicykliska grupper , Dic _n = Q _{4 n} , ordning 4 n :

Dic ₂ = Q ₈	Dic ₃ = Q ₁₂	Dic ₄ = Q ₁₆	Dic ₅ = Q ₂₀	Dic ₆ = Q ₂₄

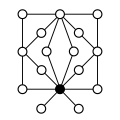
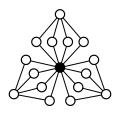
Andra direkta produkter :

Z ₄ × Z ₂	Z ₄ × Z ₂²	Z ₆ × Z ₂	Z ₈ × Z ₂	Z ₄²

Symmetriska grupper – Den symmetriska gruppen S _n innehåller, för vilken grupp som helst av ordningen n , en undergrupp som är isomorf till den gruppen. Således kommer cykelgrafen för varje grupp av ordning n att hittas i cykelgrafen för _Sn . Se exempel: Undergrupper av S ₄

Exempel: Undergrupper av hela oktaedriska gruppen

S ₄ × Z ₂

A ₄ × Z ₂

Dih ₄ × Z ₂

S ₃ × Z ₂

Hela oktaedriska gruppen är den direkta produkten $S_{4}\ gånger Z_{2}$ av den symmetriska gruppen S ₄ och den cykliska gruppen Z ₂ . Dess ordning är 48, och den har undergrupper av varje ordning som delar 48.

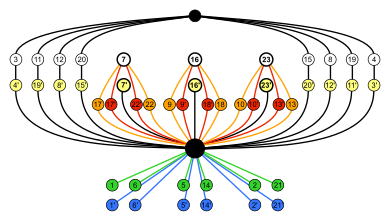
I exemplen nedan är noder som är relaterade till varandra placerade bredvid varandra, så dessa är inte de enklaste möjliga cykelgraferna för dessa grupper (som de till höger).

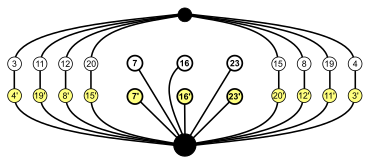
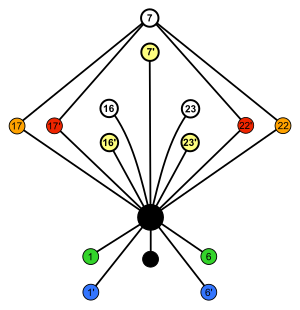
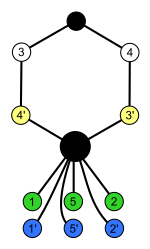
S ₄ × Z ₂ (order 48)	A ₄ × Z ₂ (ordning 24)	Dih ₄ × Z ₂ (beställning 16)	S ₃ × Z ₂ = Dih ₆ (ordning 12)


S ₄ (ordning 24)	A ₄ (ordning 12)	Dih ₄ (ordning 8)	S ₃ = Dih ₃ (ordning 6)

Liksom alla grafer kan en cykelgraf representeras på olika sätt för att framhäva olika egenskaper. De två representationerna av cykeldiagrammet för S ₄ är ett exempel på det.

Cykeldiagrammet för S ₄ som visas ovan framhäver de tre Dih ₄ -undergrupperna.

Denna annorlunda representation understryker symmetrin som ses i inversionsuppsättningarna till höger.

Se även

externa länkar

Weisstein, Eric W. "Cykeldiagram" . MathWorld .

Skiena, S. (1990). Cyklar, stjärnor och hjul. Implementering av diskret matematik: kombinatorik och grafteori med Mathematica (s. 144-147).
Shanks, Daniel (1978) [1962], Solved and Unsolved Problems in Number Theory (2nd ed.), New York: Chelsea Publishing Company, ISBN 0-8284-0297-3
Pemmaraju, S., & Skiena, S. (2003). Cyklar, stjärnor och hjul. Beräkningsdiskret matematik: kombinatorik och grafteori med Mathematica (s. 248-249). Cambridge University Press.