Binär GCD-algoritm

Visualisering av att använda den binära GCD-algoritmen för att hitta den största gemensamma divisorn (GCD) av 36 och 24. Således är GCD 2 2 × 3 = 12.

Den binära GCD-algoritmen , även känd som Steins algoritm eller den binära euklidiska algoritmen , är en algoritm som beräknar den största gemensamma delaren av två icke-negativa heltal. Steins algoritm använder enklare aritmetiska operationer än den konventionella euklidiska algoritmen ; den ersätter division med aritmetiska skift , jämförelser och subtraktion.

Även om algoritmen i sin samtida form först publicerades av den israeliska fysikern och programmeraren Josef Stein 1967, kan den ha varit känd på 200-talet f.Kr., i det antika Kina.

Algoritm

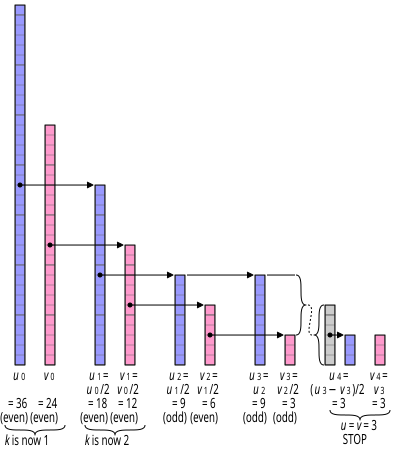
Algoritmen minskar problemet med att hitta GCD för två icke-negativa tal v och u genom att upprepade gånger tillämpa dessa identiteter:

  1. gcd(0, v ) = v , eftersom allt delar noll, och v är det största talet som delar v . På liknande sätt, gcd( u , 0) = u .
  2. gcd( 2u , 2v ) = 2·gcd( u , v )
  3. gcd( 2u , v ) = gcd( u , v ), om v är udda (2 är inte en gemensam divisor). På liknande sätt, gcd( u , 2v ) = gcd( u , v ) om u är udda.
  4. gcd( u , v ) = gcd(| u − v |, min( u , v )), om u och v båda är udda.

Genomförande

Även om ovanstående beskrivning av algoritmen är matematiskt korrekt, skiljer sig prestandaprogramvaruimplementationer vanligtvis från den på några anmärkningsvärda sätt:

  • undvika provdelning med 2 till förmån för en enda bitförskjutning och räkningen efter nollor primitiv; detta är funktionellt likvärdigt med att upprepade gånger tillämpa identitet 3, men mycket snabbare;
  • uttrycka algoritmen iterativt snarare än rekursivt : den resulterande implementeringen kan läggas ut för att undvika upprepat arbete, anropa identitet 2 i början och bibehålla som invariant att båda talen är udda när de går in i slingan, som bara behöver implementera identiteterna 3 och 4;
  • gör slingans kropp grenfri förutom dess utgångsvillkor ( v == 0 ): i exemplet nedan kompileras utbytet av u och v (som säkerställer u ≤ v ) till villkorliga rörelser ; svårförutsägbara grenar kan ha en stor negativ inverkan på prestandan.

Följande är en implementering av algoritmen i Rust som exemplifierar dessa skillnader, anpassad från uutils : 

       
     
     

    
       0 
         
         0 
         
    

    
    
    
           
           
        

     
        
              
              

        
            
               
        
        

        
          
        

        
        
           0 
               
        

        
          
        
    
 pub  fn  gcd  (  mut  u  :  u64  ,  mut  v  :  u64  )  ->  u64  {  använd  std  ::  cmp  ::  min  ;  använd  std  ::  mem  ::  swap  ;  // Basfall: gcd(n, 0) = gcd(0, n) = n  om  u  ==  {  return  v  ;  }  annat  om  v  ==  {  returnera  u  ;  }  // Använda identiteter 2 och 3:  // gcd(2ⁱ u, 2ʲ v) = 2ᵏ gcd(u, v) med u, v udda och k = min(i, j) // 2ᵏ  är den största potensen av två som delar både u och v  låt  i  =  u  .  efterföljande_nollor  ();  u  >>=  i  ;  låt  j  =  v  .  efterföljande_nollor  ();  v  >>=  j  ;  låt  k  =  min  (  i  ,  j  );  loop  {  /// u och v är udda i början av loopen  debug_assert!  (  u  %  2  ==  1  ,  "u = {} är jämnt" ,  u  )  ;  debug_assert!  (  v  %  2  ==  1  ,  "v = {} är jämnt" ,  v  )  ;  // Byt om det behövs så u <= v  if  u  >  v  {  swap  (  &  mut  u  ,  &  mut  v  );  }  /// u och v är fortfarande båda udda efter (potentiellt) byte  // Använda identitet 4 (gcd(u, v) = gcd(|vu|, min(u, v))  v  -=  u  ;  /// v är nu jämnt, men u är oförändrat (och udda)  // Identitet 1: gcd(u, 0) = u  // Skiftet med k är nödvändigt för att addera tillbaka 2ᵏ-faktorn som togs bort före loopen  om  v  ==  {  return  u  <<  k  ;  }  // Identitet 3: gcd(u, 2ʲ v) = gcd(u, v) (u är känt för att vara udda)  v  >>=  v  .  trailing_zeros  ();  /// v är nu udda igen  }  }

Komplexitet

Algoritmen kräver O ( n ) steg, där n är antalet bitar i det största av de två talen, eftersom vartannat steg reducerar minst en av operanderna med minst en faktor 2. Varje steg involverar bara några få aritmetik operationer (O(1) med en liten konstant); när man arbetar med tal i ordstorlek översätts varje aritmetisk operation till en enda maskinoperation, så antalet maskinoperationer är i storleksordningen n , dvs log₂(max( u , v )).

För godtyckliga tal är den asymptotiska komplexiteten för denna algoritm O(n 2 ), eftersom varje aritmetisk operation (subtrahera och skifta) på heltal av godtycklig storlek involverar ett linjärt antal maskinoperationer (en per ord i talens binära representation). Denna gräns reduceras till O(n² / log₂ n) när man antar att (inmatade) talen kan representeras i den (abstrakta) maskinens minne, dvs maskinens ord kan representera varje nummers storlek .

Detta är samma som för den euklidiska algoritmen, även om en mer exakt analys av Akhavi och Vallée visade att binär GCD använder cirka 60 % färre bitoperationer.

Tillägg

Den binära GCD-algoritmen kan utökas på flera sätt, antingen för att mata ut ytterligare information, hantera godtyckligt stora heltal mer effektivt eller för att beräkna GCD i andra domäner än heltal.

Den utökade binära GCD- algoritmen, analog med den utökade euklidiska algoritmen , passar i den första typen av förlängning, eftersom den tillhandahåller Bézout-koefficienterna förutom GCD, dvs heltal a och b så att a·u + b·v = gcd( u , v ).

I fallet med stora heltal är den bästa asymptotiska komplexiteten O (log n M( n )), med M( n ) kostnaden för n -bitars multiplikation; detta är nästan linjärt och mycket mindre än O(n 2 ) för den binära GCD-algoritmen, även om konkreta implementeringar endast överträffar äldre algoritmer för tal större än cirka 64 kilobit ( dvs. större än 8×10 19265 ). Detta uppnås genom att utöka den binära GCD-algoritmen med hjälp av idéer från Schönhage–Strassen-algoritmen för snabb heltalsmultiplikation.

Den binära GCD-algoritmen har också utökats till andra domäner än naturliga tal, såsom Gaussiska heltal , Eisenstein-heltal , kvadratiska ringar och heltalsringar i talfält .

Historisk beskrivning

En algoritm för att beräkna GCD för två tal var känd i det antika Kina, under Han-dynastin , som en metod för att reducera bråk:

Om möjligt halvera den; annars, ta nämnaren och täljaren, subtrahera det mindre från det större och gör det växelvis för att göra dem lika. Minska med samma antal.

— Fangtian – Lantmäteri, De nio kapitlen om den matematiska konsten

Frasen "om möjligt halvera den" är tvetydig,

  • om detta gäller när något av talen blir jämna, är algoritmen den binära GCD-algoritmen;
  • om detta bara gäller när båda talen är jämna, liknar algoritmen den euklidiska algoritmen .

Se även

  1. ^ Brent, Richard P. (13–15 september 1999). Tjugo års analys av den binära euklidiska algoritmen . 1999 Oxford-Microsoft Symposium för att hedra professor Sir Antony Hoare. Oxford.
  2. ^ Brent, Richard P. (november 1999). Ytterligare analys av den binära euklidiska algoritmen (Teknisk rapport). Oxford University Computing Laboratory. arXiv : 1303.2772 . PRG TR-7-99.
  3. ^   Stein, J. (februari 1967), "Beräkningsproblem associerade med Racah algebra", Journal of Computational Physics , 1 (3): 397–405, Bibcode : 1967JCoPh...1..397S , doi : 10.1016/0021- 9991(67)90047-2 , ISSN 0021-9991
  4. ^ a b   Knuth, Donald (1998), Seminumeriska algoritmer , konsten att programmera , vol. 2 (3:e upplagan), Addison-Wesley, ISBN 978-0-201-89684-8
  5. ^ a b Zhang, Shaohua (5 oktober 2009). "Begreppet primtal och algoritmen för att räkna den största gemensamma divisorn i det antika Kina". arXiv : 0910.0095 [ math.HO ].
  6. ^ Godbolt, Matt. "Compiler Explorer" . Hämtad 15 februari 2023 .
  7. ^ Kapoor, Rajiv (21 februari 2009). "Undvika kostnaden för felbedömning av grenen" . Intel Developer Zone .
  8. ^ Lemire, Daniel (15 oktober 2019). "Felförutsagda grenar kan multiplicera dina löptider" .
  9. ^ "GNU MP 6.1.2: Binär GCD" .
  10. ^   Akhavi, Ali; Vallée, Brigitte (2000), "Average Bit-Complexity of Euclidean Algorithms" , Proceedings ICALP'00, Lecture Notes Computer Science 1853 : 373–387, CiteSeerX 10.1.1.42.7616
  11. ^ Knuth 1998 , sid. 646, svar på övning 39 i avsnitt 4.5.2
  12. ^   Menezes, Alfred J.; van Oorschot, Paul C.; Vanstone, Scott A. (oktober 1996). "§14.4 Största gemensamma delarealgoritmer" (PDF) . Handbok för tillämpad kryptografi . CRC Tryck. s. 606–610. ISBN 0-8493-8523-7 . Hämtad 9 september 2017 .
  13. ^   Cohen, Henri (1993). "Kapitel 1: Grundläggande talteoretiska algoritmer". En kurs i beräkningsalgebraisk talteori . Graduate Texts in Mathematics . Vol. 138. Springer-Verlag . s. 17–18. ISBN 0-387-55640-0 .
  14. ^     Stehlé, Damien; Zimmermann, Paul (2004), "En binär rekursiv gcd-algoritm" (PDF) , Algoritmisk talteori , Lecture Notes in Comput. Sci., vol. 3076, Springer, Berlin, s. 411–425, CiteSeerX 10.1.1.107.8612 , doi : 10.1007/978-3-540-24847-7_31 , ISBN 978-3-540-212 , INMR 560-212 , INMR 560-212 , 10. RR-5050 .
  15. ^ Weilert, André (juli 2000). "(1+i)-är GCD-beräkning i Z[i] som en analog till den binära GCD-algoritmen" . Journal of Symbolic Computation . 30 (5): 605–617. doi : 10.1006/jsco.2000.0422 .
  16. ^ Damgård, Ivan Bjerre; Frandsen, Gudmund Skovbjerg (12–15 augusti 2003). Effektiva algoritmer för GCD och Cubic Residuosity i Ring of Eisenstein Heltal . 14:e internationella symposiet om beräkningsteoris grunder. Malmö , Sverige. s. 109–117. doi : 10.1007/978-3-540-45077-1_11 .
  17. ^ Agarwal, Saurabh; Frandsen, Gudmund Skovbjerg (13–18 juni 2004). Binära GCD-liknande algoritmer för vissa komplexa kvadratiska ringar . Symposium för algoritmisk talteori. Burlington, VT , USA. s. 57–71. doi : 10.1007/978-3-540-24847-7_4 .
  18. ^ Agarwal, Saurabh; Frandsen, Gudmund Skovbjerg (20–24 mars 2006). En ny GCD-algoritm för kvadratiska nummerringar med unik faktorisering . 7:e latinamerikanska symposiet om teoretisk informatik. Valdivia, Chile. s. 30–42. doi : 10.1007/11682462_8 .
  19. ^ Wikström, Douglas (11–15 juli 2005). På l-Ary GCD-algoritmen i Rings of Integers . Automater, språk och programmering, 32:a internationella kollokviet. Lissabon, Portugal. s. 1189–1201. doi : 10.1007/11523468_96 .

Vidare läsning

Täcker den utökade binära GCD och en probabilistisk analys av algoritmen.

Täcker en mängd olika ämnen, inklusive den utökade binära GCD-algoritmen som matar ut Bézout-koefficienter , effektiv hantering av flerprecisionsheltal med en variant av Lehmers GCD-algoritm och förhållandet mellan GCD och fortsatta bråkexpansion av reella tal.

En analys av algoritmen i det genomsnittliga fallet, genom linsen av funktionell analys : algoritmernas huvudparametrar gjuts som ett dynamiskt system , och deras medelvärde är relaterat till det invarianta måttet på systemets överföringsoperator .

externa länkar


Hämtad från " https://en.wikipedia.org/w/index.php?title=Binary_GCD_algorithm&oldid=1139483358 "