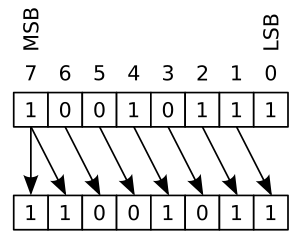
Aritmetiskt skifte

En höger aritmetisk förskjutning av ett binärt tal med 1. Den tomma positionen i den mest signifikanta biten är fylld med en kopia av den ursprungliga MSB.
En aritmetisk vänsterförskjutning av ett binärt tal med 1. Den tomma positionen i den minst signifikanta biten fylls med en nolla.
Aritmetiska skiftoperatörer i olika programmeringsspråk och processorer
Språk eller processor Vänster Höger



ActionScript 3, Java , JavaScript , Python , PHP , Ruby , C , C++ , D , C# , Go , Julia , Rust (endast signerade typer), Swift (endast signerade typer) 		< >>
Ada Skift_Vänster Shift_Right_Aritmetic
Kotlin shl shr
Standard ML < ~>>
Verilog << >>>
OpenVMS makrospråk @
Schema aritmetisk-skifte
Vanlig Lisp aska
Ocaml lsl asr
Haskell Data.Bits.shift
Montering, 68k ASL ASR
Montering, x86 SAL SAR
VHDL sla sra
RISC-V sll , slli sra , srai
Z80 SLA SRA

I datorprogrammering är ett aritmetiskt skift en skiftoperatör , ibland kallad ett undertecknat skift (även om det inte är begränsat till undertecknade operander). De två grundläggande typerna är det aritmetiska vänsterskiftet och det aritmetiska högerskiftet . För binära tal är det en bitvis operation som skiftar alla bitar i sin operand; varje bit i operanden flyttas helt enkelt ett givet antal bitpositioner, och de lediga bitpositionerna fylls i. Istället för att fyllas med alla nollor, som i logisk skiftning , när man skiftar till höger, blir biten längst till vänster ( vanligtvis teckenbit i heltalsrepresentationer med tecken) replikeras för att fylla i alla lediga positioner (detta är ett slags teckenförlängning ) .

Vissa författare föredrar termerna klibbigt högerskift och nollfyll högerskift för aritmetiska respektive logiska skift.

Aritmetiska skift kan vara användbara som effektiva sätt att utföra multiplikation eller division av tecken med heltal med två potenser. Att skifta vänster med n bitar på ett binärt tal med eller utan tecken har effekten att det multipliceras med 2 n . Att skifta åt höger med n bitar på ett binärt tal med två komplementförtecknade har effekten att det divideras med 2 n , men det avrundas alltid nedåt (mot negativ oändlighet). Detta skiljer sig från hur avrundning vanligtvis görs i heltalsdivision med tecken (som avrundar mot 0). Denna diskrepans har lett till buggar i ett antal kompilatorer.

Till exempel, i x86-instruktionsuppsättningen , dividerar SAR-instruktionen (arithmetic right shift) ett tecken med en potens av två, och avrundar mot negativ oändlighet. Däremot delar IDIV-instruktionen (signed divide) ett signerat tal och avrundar mot noll. Så en SAR-instruktion kan inte ersätta en IDIV med kraft av två-instruktioner eller vice versa.

Formell definition

Den formella definitionen av ett aritmetiskt skifte, från Federal Standard 1037C är att det är:

En förskjutning, som tillämpas på representationen av ett tal i ett numereringssystem med fixerad radix och i ett system med fixpunktsrepresentation, och där endast tecknen som representerar fixpunktsdelen av talet flyttas. En aritmetisk förskjutning är vanligtvis ekvivalent med att multiplicera talet med en positiv eller en negativ integralpotens av radixen, förutom effekten av eventuell avrundning; jämför det logiska skiftet med det aritmetiska skiftet, speciellt i fallet med flyttalsrepresentation .

Ett viktigt ord i FS 1073C-definitionen är "vanligtvis".

Ekvivalens av aritmetiska och logiska vänsterförskjutningar och multiplikation

Aritmetiska vänsterförskjutningar är ekvivalenta med multiplikation med en (positiv, integral) potens av radixen (t.ex. en multiplikation med en potens av 2 för binära tal). Logiska vänsterskift är också ekvivalenta, förutom multiplikation och aritmetiska skift kan utlösa aritmetiskt spill medan logiska skift inte gör det.

Icke-ekvivalens av aritmetisk högerförskjutning och division

Men aritmetiska högerförskjutningar är stora fällor för de oförsiktiga, speciellt vid behandling av avrundning av negativa heltal. Till exempel, i den vanliga tvåkomplementrepresentationen av negativa heltal, representeras −1 som alla 1:or. För ett 8-bitars heltal med tecken är detta 1111 1111. En aritmetisk högerförskjutning med 1 (eller 2, 3, ..., 7) ger 1111 1111 igen, vilket fortfarande är −1. Detta motsvarar avrundning nedåt (mot negativ oändlighet), men är inte den vanliga konventionen för division.

Det sägs ofta att aritmetiska högerskift är ekvivalenta med division med en (positiv, integral) potens av radixen (t.ex. en division med en potens av 2 för binära tal), och därför kan division med en potens av radixen vara optimeras genom att implementera det som ett aritmetiskt högerskifte. (En växlingsreglage är mycket enklare än en avdelare. På de flesta processorer kommer växlingsinstruktioner att utföras snabbare än delningsinstruktioner.) Stort antal 1960- och 1970-tals programmeringshandböcker, manualer och andra specifikationer från företag och institutioner som DEC , IBM , Data General och ANSI gör sådana felaktiga påståenden [ sida behövs ] .

Logiska högerförskjutningar motsvarar division med en potens av radixen (vanligtvis 2) endast för positiva eller otecknade tal. Aritmetiska högerförskjutningar är ekvivalenta med logiska högerförskjutningar för tal med positivt tecken. Aritmetiska högerförskjutningar för negativa tal i N−1:s komplement (vanligtvis tvås komplement ) motsvarar ungefär division med en potens av radixen (vanligtvis 2), där för udda tal avrundning nedåt tillämpas (inte mot 0 som man brukar förvänta sig).

Aritmetiska högerförskjutningar för negativa tal är likvärdiga med division med avrundning mot 0 i ens komplementrepresentation av tecken som användes av vissa historiska datorer, men detta är inte längre i allmänt bruk.

Hantera problemet i programmeringsspråk

ISO-standarden (1999) för programmeringsspråket C definierar den högra skiftoperatorn i termer av divisioner med potenser 2. På grund av den ovan angivna icke-ekvivalensen, utesluter standarden uttryckligen från den definitionen de högra skiftningarna av teckental som har negativa värden. Den specificerar inte beteendet hos rätt skiftoperatör under sådana omständigheter, utan kräver istället att varje enskild C-kompilator definierar beteendet för att skifta negativa värden åt höger.

Ansökningar

I applikationer där konsekvent avrundning nedåt önskas är aritmetiska högerförskjutningar för teckenvärden användbara. Ett exempel är att nedskala rasterkoordinater med en potens av två, vilket bibehåller jämnt avstånd. Till exempel, högerförskjutning med 1 skickar 0, 1, 2, 3, 4, 5, ... till 0, 0, 1, 1, 2, 2, ... och −1, −2, −3, −4, ... till −1, −1, −2, −2, ..., med jämnt avstånd som −2, −2, −1, −1, 0, 0, 1, 1, 2, 2 , ... Däremot skickar heltalsdivision med avrundning mot noll −1, 0 och 1 alla till 0 (3 poäng istället för 2), vilket ger −2, −1, −1, 0, 0, 0, 1, 1, 2, 2, ... istället, vilket är oregelbundet vid 0.

Anteckningar

  1. ^ Operatorn >> i C och C++ är inte nödvändigtvis ett aritmetiskt skift. Vanligtvis är det bara ett aritmetiskt skift om det används med en heltalstyp med tecken på vänster sida. Om det istället används på en heltalstyp utan tecken, blir det ett logiskt skifte.
  2. ^ Verilogs aritmetiska högerskiftsoperator utför faktiskt bara ett aritmetiskt skift om den första operanden är signerad. Om den första operanden är osignerad, utför operatören faktiskt ett logiskt högerskifte.
  3. ^ I makrospråket OpenVMS bestäms om ett aritmetiskt skift är vänster eller höger av om den andra operanden är positiv eller negativ. Detta är ovanligt. I de flesta programmeringsspråk har de två riktningarna distinkta operatorer, där operatorn anger riktningen och den andra operanden är implicit positiv. (Vissa språk, som Verilog, kräver att negativa värden konverteras till osignerade positiva värden. Vissa språk, som C och C++, har inget definierat beteende om negativa värden används.) [ sida behövs ]
  4. ^ I Scheme kan aritmetisk skift vara både vänster och höger skift, beroende på den andra operanden, mycket likt OpenVMS makrospråk, även om R6RS Scheme lägger till både -höger och -vänster varianter.
  5. ^ Bits - klassen från Haskells Data.Bits -modul definierar både shift som tar ett signerat argument och shiftL / shiftR tar osignerade argument. Dessa är isomorfa ; för nya definitioner behöver programmeraren endast tillhandahålla en av de två formerna och den andra formen kommer automatiskt att definieras i termer av den tillhandahållna.
  6. ^ VHDL aritmetiska vänsterskiftsoperatören är ovanlig. Istället för att fylla i LSB för resultatet med noll, kopierar den den ursprungliga LSB till den nya LSB. Även om detta är en exakt spegelbild av den aritmetiska högerförskjutningen, är det inte den konventionella definitionen av operatorn och är inte ekvivalent med multiplikation med en potens av 2. I VHDL 2008-standarden lämnades detta konstiga beteende oförändrat (för bakåtkompatibilitet) ) för argumenttyper som inte har påtvingad numerisk tolkning (t.ex. BIT_VECTOR) men 'SLA' för osignerade och signerade argumenttyper beter sig på det förväntade sättet (dvs. positionerna längst till höger fylls med nollor). VHDL:s logiska skift åt vänster (SLL)-funktion implementerar det ovan nämnda "standard" aritmetiska skiftet.
  7. ^ C-standarden var avsedd att inte begränsa C-språket till antingen ens komplement eller tvås komplementarkitektur. I de fall där beteendet hos ens komplement och tvås komplementrepresentationer skiljer sig, som detta, kräver standarden att enskilda C-kompilatorer dokumenterar beteendet hos sina målarkitekturer. Dokumentationen för GNU Compiler Collection (GCC), till exempel, dokumenterar dess beteende som att använda teckenförlängning.

Korsreferens

Använda källor

Public Domain Den här artikeln innehåller material från allmän egendom från Federal Standard 1037C . General Services Administration . Arkiverad från originalet 2022-01-22.

Hämtad från " https://en.wikipedia.org/w/index.php?title=Arithmetic_shift&oldid=1121633413 "