Räknesticka

En typisk 25 cm skjutregel för elever (Pickett N902-T simplex trig), även känd i vardagsspråket i USA som en slipstick

Glidregeln är en mekanisk analog dator som används främst för multiplikation och division och för funktioner som exponenter , rötter , logaritmer och trigonometri . Det är vanligtvis inte utformat för addition eller subtraktion, vilket vanligtvis utförs med andra metoder, som att använda en abacus . Maximal noggrannhet för vanliga linjära diaregler är cirka tre decimaler signifikanta siffror, medan vetenskaplig notation används för att hålla reda på resultatens storleksordning .

Reglar finns i en mängd olika stilar och förekommer vanligtvis i linjär, cirkulär eller cylindrisk form, med linjalskalor inskrivna med standardiserade graderade markeringar. Slidregler tillverkade för specialiserade områden som flyg eller finans har vanligtvis ytterligare skalor som hjälper till med specialiserade beräkningar som är specifika för dessa områden. Slidregeln är nära relaterad till nomogram som används för applikationsspecifika beräkningar. Även om den liknar en vanlig linjal till namn och utseende, är den inte avsedd att användas för att mäta längd eller rita raka linjer.

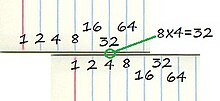
Som enklast representeras varje tal som ska multipliceras av en längd på ett par parallella linjaler som kan glida förbi varandra. Eftersom linjalerna var och en har en logaritmisk skala, är det möjligt att rikta in dem för att läsa summan av talens logaritmer och därmed beräkna produkten av de två talen.

Den engelske matematikern och prästen pastor William Oughtred och andra utvecklade glidregeln på 1600-talet baserat på John Napiers framväxande arbete om logaritmer . Före tillkomsten av den vetenskapliga fickkalkylatorn var det det mest använda beräkningsverktyget inom vetenskap och teknik . Glidregelns enkla användning, lättillgängliga och låga kostnad gjorde att användningen fortsatte att växa under 1950- och 1960-talen, även när elektroniska datorer gradvis introducerades. Introduktionen av den handhållna elektroniska vetenskapliga kalkylatorn cirka 1974 gjorde att skjutreglerna i stort sett föråldrades, och de flesta leverantörer lämnade verksamheten.

Grundläggande koncept

Markör på en skjutregel

I sin mest grundläggande form använder glidregeln två logaritmiska skalor för att utföra snabb multiplikation och division av tal. Dessa vanliga operationer kan vara tidskrävande och felbenägna när de görs på papper. Mer utarbetade diaregler kan utföra andra beräkningar, som kvadratrötter , exponentialer , logaritmer och trigonometriska funktioner .

Skalor kan grupperas i decennier, som är tal som sträcker sig från 1 till 10 (dvs. 10 ⁿ till 10 ^{n +1} ). Således sträcker sig endekadsskalorna C och D från 1 till 10 över hela linjalens längd, medan skalorna A och B med två decennier sträcker sig från 1 till 100 över linjalens längd.

I allmänhet utförs matematiska beräkningar genom att rikta in ett märke på den glidande mittremsan med ett märke på en av de fasta remsorna, och sedan observera de relativa positionerna för andra märken på remsorna. Siffror i linje med markeringarna anger det ungefärliga värdet av produkten , kvoten eller annat beräknat resultat.

Användaren bestämmer platsen för decimalkomma i resultatet, baserat på mental uppskattning. Vetenskaplig notation används för att spåra decimalkomma i mer formella beräkningar. Additions- och subtraktionssteg i en beräkning görs vanligtvis mentalt eller på papper, inte på skjutregeln.

Markera ett par registerkort och introducera bas 2 med den här hemmagjorda linjalen.

De flesta diaregler består av tre delar:

Ram eller bas – två linjära remsor av samma längd hålls parallella med ett mellanrum.
Slide – en mittremsa som är sammankopplad med ramen som kan röra sig på längden i förhållande till ramen.
Löpare eller glas – ett yttre glidstycke med hårfäste, även känd som "markören".

Vissa glidregler ("duplex"-modeller) har skalor på båda sidor av linjalen och glidremsan, andra på ena sidan av de yttre remsorna och båda sidorna av glidlisten (som vanligtvis kan dras ut, vändas och sättas in igen för bekvämlighets skull. ), ytterligare andra bara på ena sidan ("enkla" regler). En glidande markör med en vertikal inriktningslinje används för att hitta motsvarande punkter på skalor som inte ligger intill varandra eller, i duplexmodeller, är på andra sidan regeln. Markören kan också spela in ett mellanresultat på någon av skalorna.

Drift

Den här skjutregeln är placerad för att ge flera värden: Från C-skala till D-skala (multiplicera med 2), från D-skala till C-skala (dividera med 2), A- och B-skalor (multiplicera och dividera med 4), A- och D-skalor (kvadrat och kvadratrötter).

En logaritm omvandlar operationerna multiplikation och division till addition och subtraktion enligt reglerna $\log(xy)=\log(x)+ \log(y)$ och $\log(x/y)=\log(x)-\log(y)$ . Om du flyttar den översta skalan åt höger med ett avstånd på ${\displaystyle \log(x)} ,$ genom att matcha början av den översta skalan med etiketten $x$ längst ned, justeras varje nummer $y$ , vid positionslogg $\displaystyle \log(y)}$ på den översta skalan, med siffran vid positionslogg $\displaystyle \log( x)+\log(y)}$ på den nedre skalan. Eftersom $\log(x)+\log(y)=\log(xy)$ ger denna position på den nedre skalan $xy$ , produkten av $x$ och $y$ .

Multiplikation

För att multiplicera 3×2 flyttas 1:an på den översta skalan till 2:an på den nedre skalan. Svaret, 6, läses av den nedre skalan där 3 är på den översta skalan.

För att multiplicera 7×2 flyttas 1:an på den översta skalan till 2:an på den nedre skalan. Svaret, 14, läses av den nedre skalan där 7 är på den översta skalan. Eftersom 7:an är ovanför den andra uppsättningen siffror måste resultatet multipliceras med 10. Så även om svaret direkt är 1,4 är det korrekta svaret 1,4 x 10 = 14.

För att multiplicera 88x20 flyttas 1:an på den översta skalan till 2:an på den nedre skalan. Eftersom 2 representerar 20 multipliceras alla tal i den skalan med 10, så alla svar i den andra uppsättningen siffror multipliceras med 100. Eftersom 8,8 i den översta skalan representerar 88, måste svaret dessutom multipliceras med 10. Svaret svarar direkt står på 1,76. Multiplicera med 100 och sedan med 10 för att få det faktiska svaret: 1 760.

I allmänhet flyttas 1:an överst till en faktor på botten, och svaret läses av längst ner där den andra faktorn är överst. Detta fungerar eftersom avstånden från "1" är proportionella mot logaritmerna för de markerade värdena.

Division

Illustrationen nedan visar beräkningen av 5,5/2. 2:an på den översta skalan placeras över 5,5:an på den nedre skalan. 1:an på den översta skalan ligger ovanför kvoten, 2,75. Det finns mer än en metod för att göra division, och metoden som presenteras här har fördelen att slutresultatet inte kan vara off-scale, eftersom man kan välja att använda 1:an i vardera änden.

Med mer komplexa beräkningar som involverar flera faktorer i täljaren och nämnaren för ett uttryck, kan rörelser av skalorna minimeras genom alternerande divisioner och multiplikationer. Således skulle (5,5×3)/2 beräknas som (5,5/2)×3 och resultatet, 8,25, kan avläsas under 3:an i den översta skalan i figuren ovan, utan att behöva registrera mellanresultatet för 5,5 /2.

Övriga operationer

Förutom de logaritmiska skalorna har vissa skjutregler andra matematiska funktioner kodade på andra hjälpskalor. De mest populära är trigonometrisk , vanligtvis sinus och tangens , vanlig logaritm (log 10 ) (för att ta logaritmen av ett värde på en multiplikatorskala), naturlig logaritm (ln) och exponentiell ( e ^x ) skalor. Vissa regler inkluderar en pytagoreisk ("P") skala för att lösa trianglar. Andra har skalor för att beräkna hyperboliska funktioner . På linjära regler är skalorna och deras märkning högst standardiserade, med variationer som vanligtvis bara förekommer när det gäller vilka skalor som ingår och i vilken ordning:

A, B	två decenniers logaritmiska skalor, två sektioner som var och en är halva längden av C- och D-skalorna, används för att hitta kvadratrötter och kvadrater av tal
CD	logaritmiska skalor med ett decennium, enstaka sektioner av samma längd, som används tillsammans för multiplikation och division, och vanligtvis kombineras en av dem med en annan skala för andra beräkningar
K	tre decenniers logaritmisk skala, tre sektioner som var och en är en tredjedel av längden på C- och D-skalorna, används för att hitta kubrötter och kuber av tal
CF, DF	"vikta" versioner av C- och D-skalorna som börjar från π snarare än från enhet; dessa är praktiska i två fall. Först när användaren gissar att en produkt kommer att vara nära 10 och inte är säker på om den kommer att vara något mindre eller något mer än 10, undviker de vikta vågen möjligheten att gå av vågen. För det andra, genom att göra starten π snarare än kvadratroten ur 10, förenklas multiplicering eller division med π (som är vanligt i formler för vetenskap och teknik).
CI, DI, CIF, DIF	"inverterade" skalor, som går från höger till vänster, används för att förenkla 1/ x steg
S	används för att hitta sinus och cosinus på C (eller D) skalan
T, T1, T2	används för att hitta tangenter och cotangenter på C- och CI-skalorna (eller D och DI).
R1, R2	kvadratrotsskalor – ställ in markören till valfritt värde $r$ på R1 eller R2, hitta ${\pi }r^{2}$ (area av en cirkel med radie $r$ ) under markören på DF-skalan
ST, SRT	används för sinus och tangenter för små vinklar och grad-radianomvandling
Sh, Shl, Sh2	används för att hitta hyperboliska sinus på C (eller D) skalan
Ch	används för att hitta hyperboliska cosinus på C (eller D) skalan
Th	används för att hitta hyperboliska tangenter på C (eller D) skalan
L	en linjär skala, som används tillsammans med C- och D-skalorna för att hitta bas-10 logaritmer och potenser av 10
LL0N (eller LL/N) och LLN	log-loggen vikta $e^{-x}$ och $e^{x}$ skalorna, för att arbeta med logaritmer av valfri bas och godtyckliga exponenter. 4, 6 eller 8 skalor av denna typ ses ofta.
Ln	en linjär skala, som används tillsammans med C- och D-skalorna för att hitta naturliga (bas $e$ ) logaritmer och $e^{x}$

Vågen på fram- och baksidan av en Keuffel and Esser (K&E) 4181-3 linjal

Binary Slide Rule tillverkad av Gilson 1931 utförde en additions- och subtraktionsfunktion begränsad till bråk.

Rötter och krafter

Det finns skalor för enstaka årtionden (C och D), dubbeldekadsskalor (A och B) och tredekadsskalor (K). För att beräkna $x^{2}$ till exempel, lokalisera x på D-skalan och läs dess kvadrat på A-skalan. Genom att invertera denna process kan kvadratrötter hittas, och på samma sätt för potenserna 3, 1/3, 2/3 och 3/2. Försiktighet måste iakttas när basen, x, finns på mer än ett ställe på skalan. Till exempel finns det två nior på A-skalan; för att hitta kvadratroten ur nio, använd den första; den andra ger kvadratroten av 90.

För $x^{y}$ problem, använd LL-skalorna. När flera LL-skalor finns, använd den med x på. Rikta först in den 1:an längst till vänster på C-skalan med x på LL-skalan. Hitta sedan y på C-skalan och gå ner till LL-skalan med x på. Den skalan kommer att indikera svaret. Om y är "utanför skalan", leta reda på $x^{y/2}$ och kvadrat med A- och B-skalorna enligt beskrivningen ovan. Alternativt, använd 1:an längst till höger på C-skalan och läs svaret från nästa högre LL-skala. Om du till exempel justerar 1:an längst till höger på C-skalan med 2 på LL2-skalan, 3 på C-skalan i linje med 8 på LL3-skalan.

För att extrahera en kubrot med hjälp av en linjal med endast C/D- och A/B-skalor, rikta in 1 på B-markören med basnumret på A-skalan (var noga med att som alltid skilja mellan den nedre och övre halvan av A skala). Skjut bilden tills siffran på D-skalan som är mot 1 på C-markören är densamma som siffran på B-markören som är mot bastalet på A-skalan. (Exempel: A 8, B 2, C 1, D 2; A 27, B 3, C 1, D 3.)

Rötter till andragradsekvationer

Andragradsekvationer av formen $ax^{2}+bx+c=0$ kan lösas genom att först reducera ekvationen till formen ${\ displaystyle x^{2}-px+q=0}$ (där $p=-b/a$ och $q=c/a$ ), och sedan justera index ("1") för C-skalan till värdet $q$ på D-skalan. Markören flyttas sedan längs regeln tills en position hittas där siffrorna på CI- och D-skalorna summerar till $p$ . Dessa två värden är rötterna till ekvationen.

Trigonometri

S-, T- och ST-skalorna används för trigfunktioner och multiplar av trigfunktioner, för vinklar i grader.

För vinklar från cirka 5,7 upp till 90 grader hittas sinus genom att jämföra S-skalan med C (eller D)-skalan. (I många regler för sluten kropp relaterar S-skalan istället till A- och B-skalorna och täcker vinklar från cirka 0,57 upp till 90 grader; det som följer måste justeras på lämpligt sätt.) S-skalan har en andra uppsättning vinklar (ibland i en annan färg), som löper i motsatt riktning och används för cosinus. Tangenter hittas genom att jämföra T-skalan med C (eller D)-skalan för vinklar mindre än 45 grader. För vinklar större än 45 grader används CI-skalan. Vanliga former som $k\sin x$ kan läsas direkt från x på S-skalan till resultatet på D-skalan, när C-skalans index är satt till k . För vinklar under 5,7 grader är sinus, tangenter och radianer ungefär lika stora och återfinns på ST- eller SRT-skalan (sinus, radianer och tangenter), eller helt enkelt dividerat med 57,3 grader/ radian . Omvända trigonometriska funktioner hittas genom att vända processen.

Många skjutregler har S-, T- och ST-skalor markerade med grader och minuter (t.ex. vissa Keuffel- och Esser-modeller (t.ex. Doric duplex 5"-modeller), regler av senmodell Teledyne-Post Mannheim-typ). Så kallad decitrig modeller använder decimalfraktioner av grader istället.

Logaritmer och exponentialer

Bas-10 logaritmer och exponentialer hittas med hjälp av L-skalan, som är linjär. Vissa glidregler har en Ln-skala, som är för basen e. Logaritmer till vilken annan bas som helst kan beräknas genom att omvända proceduren för att beräkna potenser av ett tal. Till exempel kan log2-värden bestämmas genom att rada upp 1 längst till vänster eller längst till höger på C-skalan med 2 på LL2-skalan, hitta talet vars logaritm ska beräknas på motsvarande LL-skala och läsa av log2-värdet på C skala.

Addition och subtraktion

Bildregler används vanligtvis inte för addition och subtraktion. Det är möjligt att göra det med två olika tekniker.

Den första metoden för att utföra addition och subtraktion på C och D (eller någon jämförbar skala) kräver att problemet konverteras till ett med division. För addition är kvoten av de två variablerna plus en gånger divisorn lika med deras summa:

x+y=\left({\frac {x}{y}}+1\right)y.

För subtraktion är kvoten för de två variablerna minus en gånger divisorn lika med deras skillnad:

xy=\left({\frac {x}{y}}-1\right)y.

Denna metod liknar additions-/subtraktionstekniken som används för elektroniska höghastighetskretsar med logaritmiskt talsystem i specialiserade datortillämpningar som superdatorn Gravity Pipe (GRAPE) och dolda Markov-modeller .

Den andra metoden använder en glidande linjär L-skala som finns tillgänglig på vissa modeller. Addition och subtraktion utförs genom att skjuta markören åt vänster (för subtraktion) eller höger (för addition) och sedan återställa bilden till 0 för att läsa resultatet.

Generaliseringar

Kvadratiska och reciproka skalor

Med hjälp av (nästan) alla strikt monotona skalor kan andra beräkningar också göras med en rörelse. Till exempel kan ömsesidiga skalor användas för likheten ${\frac {1}{x}}+{\frac {1}{y}}={\frac {1} {z}}$ (beräknar parallella resistanser , harmoniskt medelvärde , etc.), och kvadratiska skalor kan användas för att lösa $x^{2}+y^{2}=z^ {2}$ .

Fysisk design

Standard linjära regler

En 7 fot (2,1 m) inlärningsrutschbana jämfört med en normalstor modell

Bredden på linjalen anges i termer av skalornas nominella bredd. Vågar på de vanligaste "10-tums"-modellerna är faktiskt 25 cm, eftersom de gjordes enligt metriska standarder, även om vissa regler erbjuder något utökade skalor för att förenkla manipulation när ett resultat svämmar över. Fickreglerna är vanligtvis 5 tum (12 cm). Modeller på ett par meter (yards) breda gjordes för att hängas upp i klassrum i undervisningssyfte.

Vanligtvis markerar divisionerna en skala med en precision av två signifikanta siffror , och användaren uppskattar den tredje siffran. Vissa avancerade diaregler har förstoringsmarkörer som gör markeringarna lättare att se. Sådana markörer kan effektivt fördubbla avläsningarnas noggrannhet, vilket tillåter en 10-tums linjal att fungera såväl som en 20-tums modell.

Olika andra bekvämligheter har utvecklats. Trigonometriska skalor är ibland dubbelmärkta, i svart och rött, med kompletterande vinklar, den så kallade "Darmstadt"-stilen. Duplex reglage duplicerar ofta några av skalorna på baksidan. Vågar är ofta "delade" för att få högre noggrannhet. ^{[ ytterligare förklaring behövs ]}

Cirkulära glidregler

Cirkulära diaregler finns i två grundläggande typer, en med två markörer och en annan med en gratis maträtt och en markör. De dubbla markörversionerna utför multiplikation och division genom att hålla en konstant vinkel mellan markörerna när de roteras runt ratten. Den enfaldiga markörversionen fungerar mer som standardregeln genom lämplig justering av skalorna.

Den grundläggande fördelen med en cirkulär linjal är att verktygets bredaste dimension reducerades med en faktor på cirka 3 (dvs. med π ). Till exempel skulle en 10 cm cirkulär ha en maximal precision som är ungefär lika med en 31,4 cm vanlig linjal. Cirkulära diaregler eliminerar också "off-scale" beräkningar, eftersom vågen var designad för att "linda runt"; de behöver aldrig omorienteras när resultaten är nära 1,0 – regeln är alltid på skalan. Men för icke-cykliska icke-spiralskalor som S, T och LL:s, är skalbredden smalare för att ge plats åt ändmarginaler.

Cirkulära linjaler är mekaniskt mer robusta och smidigare, men deras precision i skalinriktningen är känslig för centreringen av en central pivot; en minut 0,1 mm (0,0039 tum) utanför mitten av pivoten kan resultera i ett 0,2 mm (0,0079 tum) värsta fallet inriktningsfel. Pivoten förhindrar repor i ansiktet och markörerna. Skalorna med högsta noggrannhet är placerade på de yttre ringarna. I stället för "delade" skalor använder avancerade cirkulära regler spiralskalor för mer komplexa operationer som log-of-log-skalor. En åtta-tums premium cirkulär regel hade en 50-tums spiral log-log skala. Runt 1970 innehöll en billig modell från BC Boykin (Model 510) 20 vågar, inklusive 50-tums CD (multiplikation) och logvågar. RotaRule hade en friktionsbroms för markören.

De största nackdelarna med cirkulära rutschbanor är svårigheten att lokalisera figurer längs ett fat och ett begränsat antal skalor. En annan nackdel med cirkulära glidregler är att mindre viktiga skalor är närmare mitten och har lägre precision. De flesta elever lärde sig användning av skjutregel på de linjära skjutreglerna och fann ingen anledning att byta.

En skjutregel som finns kvar i dagligt bruk runt om i världen är E6B . Detta är en cirkulär skjutregel som skapades först på 1930-talet för flygplanspiloter för att hjälpa till med döda räkningar . Med hjälp av skalor tryckta på ramen hjälper den också till med olika uppgifter som att konvertera tid, avstånd, hastighet och temperaturvärden, kompassfel och beräkning av bränsleförbrukning. Det så kallade "bönehjulet" finns fortfarande tillgängligt i flygaffärer och används fortfarande i stor utsträckning. Medan GPS har minskat användningen av döda räkningar för flygnavigering och handhållna miniräknare har tagit över många av dess funktioner, är E6B fortfarande allmänt använd som en primär eller reservenhet och majoriteten av flygskolor kräver att deras elever har en viss grad av skicklighet i dess användning.

Proportionhjul är enkla cirkulära skjutregler som används i grafisk design för att beräkna bildförhållanden . Om de ursprungliga och önskade storleksvärdena ställs in på de inre och yttre hjulen visas deras förhållande i procent i ett litet fönster. Även om de inte är lika vanliga sedan tillkomsten av datoriserad layout, tillverkas och används de fortfarande. ^{[ citat behövs ]}

1952 introducerade det schweiziska klockföretaget Breitling ett pilotarmbandsur med en integrerad cirkulär skjutregel specialiserad för flygberäkningar: Breitling Navitimer. Navitimers cirkulära regel, som Breitling hänvisar till som en "navigationsdator", innehöll funktioner för flyghastighet , hastighet /tid för stigning/nedstigning, flygtid, distans och bränsleförbrukning, såväl som kilometer - sjömil och gallon - liter bränslemängd konverteringsfunktioner.

En enkel cirkulär linjal, tillverkad av Concise Co., Ltd., Tokyo, Japan, med endast omvända, kvadratiska och kubiska skalor. På baksidan finns en praktisk lista med 38 metriska / imperialistiska omvandlingsfaktorer.
En rysk cirkulär skjutregel byggd som ett fickur som fungerar som en skjutlina eftersom de två nålarna är sammanfogade
En tvåskalig linjal inbyggd i en ring
Pickett cirkulär linjal med två markörer. (4,25 tum/10,9 cm bredd) Omvänd har ytterligare skala och en markör.
Breitling Navitimer armbandsur med cirkulär linjal
Framsidan av en Boykin RotaRule Model 510
Baksidan av en Boykin RotaRule Model 510

Cylindriska glidregler

Det finns två huvudtyper av cylindriska glidregler: de med spiralformade skalor som Fuller-kalkylatorn , Otis King och Bygrave-linjalen , och de med stänger, som Thacher- och vissa Loga-modeller. I båda fallen är fördelen en mycket längre skala, och därmed potentiellt större precision, än vad en rak eller cirkulär regel ger.

Fuller miniräknare, 1928
Otis King Model K
Bygrave skjutregel
Thacher skjutregel, cirka 1890

Material

Traditionellt var skjutregler gjorda av hårt trä som mahogny eller buxbom med markörer av glas och metall. Åtminstone ett högprecisionsinstrument var tillverkat av stål.

År 1895 började ett japanskt företag, Hemmi, tillverka skjutregler av celluloidklädd bambu, som hade fördelarna av att vara formstabila, starka och naturligt självsmörjande. Dessa rutschbanor i bambu introducerades i Sverige i september 1933, och förmodligen bara lite tidigare i Tyskland.

Vågar tillverkades också av celluloid eller andra polymerer, eller trycktes på aluminium. Senare markörer gjuts av akryl eller polykarbonat , ibland med teflonbärande ytor.

Alla premium glidregler hade siffror och skalor djupt ingraverade och sedan fyllda med färg eller annat harts . Målade eller präglade glidregler ansågs vara sämre eftersom markeringarna kunde slitas av eller skadas kemiskt. Ändå tillverkade Pickett, ett amerikanskt skjutreglerföretag, endast tryckta skalaregler. Premium glidregler innehöll smarta spärrar så att regeln inte skulle falla isär av misstag, och stötfångare för att skydda vågen och markören från att skava på bordsskivor.

Historia

William Oughtred (1575–1660), uppfinnare av skjutregeln

1763 illustration av en linjal

Glidregeln uppfanns omkring 1620–1630, kort efter John Napiers publicering av begreppet logaritmen . År 1620 Edmund Gunter från Oxford en beräkningsenhet med en enda logaritmisk skala; med ytterligare mätverktyg kan den användas för att multiplicera och dividera. I c. 1622 William Oughtred från Cambridge två handhållna Gunter-regler för att göra en enhet som är igenkännbar den moderna skjutregeln. Oughtred blev inblandad i en hätsk kontrovers om prioritet , med sin engångsstudent Richard Delamain och Wingates tidigare anspråk. Oughtreds idéer offentliggjordes endast i publikationer av hans elev William Forster 1632 och 1653.

År 1677 skapade Henry Coggeshall en tvåfots viklina för timmermått, kallad Coggeshall glidregel , vilket utökade användningen av rutschbanan bortom matematisk undersökning.

År 1722 introducerade Warner två- och tredecenniumsskalorna, och 1755 inkluderade Everard en omvänd skala; en linjal som innehåller alla dessa skalor är vanligtvis känd som en "polyfas"-regel.

År 1815 uppfann Peter Mark Roget regeln för logglogg, som inkluderade en skala som visar logaritmen för logaritmen. Detta gjorde det möjligt för användaren att direkt utföra beräkningar som involverade rötter och exponenter. Detta var särskilt användbart för bråkpotenser.

År 1821 beskrev Nathaniel Bowditch i American Practical Navigator en "sliding rule" som innehöll skalade trigonometriska funktioner på den fasta delen och en rad log-sines och log-tans på reglaget som användes för att lösa navigeringsproblem.

1845 introducerade Paul Cameron från Glasgow en nautisk rutschbana som kan svara på navigeringsfrågor, inklusive höger uppstigning och deklination av solen och huvudstjärnorna.

Modern form

Ingenjör som använder en linjal, med mekanisk kalkylator i bakgrunden, mitten av 1900-talet

En mer modern form av rutschbana skapades 1859 av den franske artillerielöjtnanten Amédée Mannheim , som hade turen att få sitt styre gjort av ett företag med nationellt rykte och att det antogs av det franska artilleriet. Mannheims regel hade två stora modifieringar som gjorde den lättare att använda än tidigare allmänna diaregler. Sådana regler hade fyra grundläggande skalor, A, B, C och D, och D var den enda logaritmiska skalan med ett decennium; C hade två decennier, som A och B. De flesta operationer gjordes på A- och B-skalorna; D användes endast för att hitta kvadrater och kvadratrötter. Mannheim ändrade C-skalan till en endecenniumsskala och utförde de flesta operationer med C och D istället för A och B. Eftersom C- och D-skalan var endecenniumsskala kunde de avläsas mer exakt, så regelns resultat kunde bli mer exakt. Ändringen gjorde det också lättare att ta med kvadrater och kvadratrötter som en del av en större beräkning. Mannheims regel hade också en markör, till skillnad från nästan alla föregående regler, så vilken som helst av skalorna kunde enkelt jämföras över regelytan. "Mannheim-regeln" blev standardarrangemanget för rutschhållare för det senare 1800-talet och förblev en vanlig standard under hela rutschhållarens era.

Tillväxten av ingenjörsyrket under det senare 1800-talet drev en utbredd användning av skjutreglage, som började i Europa och så småningom även i USA. Duplexregeln uppfanns av William Cox 1891 och producerades av Keuffel och Esser Co. i New York.

1881 introducerade den amerikanske uppfinnaren Edwin Thacher sin cylindriska regel, som hade en mycket längre skala än vanliga linjära regler och därmed kunde beräkna med högre precision, cirka fyra till fem signifikanta siffror. Thacher-regeln var dock ganska dyr, förutom att den inte var bärbar, så den användes i mycket mer begränsat antal än konventionella glidregler.

Astronomiskt arbete krävde också exakta beräkningar, och i Tyskland på 1800-talet användes en cirka två meter lång rutschbana i stål vid ett observatorium. Den hade ett mikroskop anslutet, vilket gav den noggrannhet till sex decimaler. ^{[ citat behövs ]}

var romanförfattaren och ingenjören Nevil Shute Norway (han kallade sin självbiografi Slide Rule ) Chief Calculator på designen av det brittiska R100 - luftskeppet för Vickers Ltd. från 1924. Spänningsberäkningarna för varje tvärgående ram krävde beräkningar av ett par miniräknare (människor) som använder Fullers cylindriska glidregler i två eller tre månader. Den samtidiga ekvationen innehöll upp till sju okända kvantiteter, tog ungefär en vecka att lösa och måste upprepas med ett annat urval av slaka trådar om gissningen på vilken av de åtta radiella ledningarna som var slaka var fel och en av ledningarna gissade till vara slapp var inte slapp. Efter månader av arbete med att fylla kanske femtio foolscap-ark med beräkningar "sanningen avslöjades" (och) gav en tillfredsställelse som nästan uppgick till en religiös upplevelse".

Under hela 1950- och 1960-talen var skjutregeln symbolen för ingenjörsyrket på samma sätt som stetoskopet är det för läkarkåren.

Den tyske raketforskaren Wernher von Braun köpte två Nestler- rutschregler på 1930-talet. Tio år senare tog han dem med sig när han flyttade till USA efter andra världskriget för att arbeta med den amerikanska rymdsatsningen . Under hela sitt liv använde han aldrig någon annan skjutregel. Han använde sina två Nestlers när han ledde NASA- programmet som landade en man på månen i juli 1969.

Aluminium Pickett-märke rutschbanor bars på Project Apollo rymduppdrag. Modellen N600-ES som ägs av Buzz Aldrin och som flög med honom till månen på Apollo 11 såldes på auktion 2007. Modellen N600-ES som togs med på Apollo 13 1970 ägs av National Air and Space Museum .

Några ingenjörsstudenter och ingenjörer bar tiotums skjutregler i bälteshölster, en vanlig syn på campus till och med i mitten av 1970-talet. Fram till tillkomsten av den digitala fickkalkylatorn kan eleverna också ha en tio- eller tjugotumsregel för precisionsarbete hemma eller på kontoret medan de bär en femtumslinjal med sig.

År 2004 skapade utbildningsforskarna David B. Sher och Dean C. Nataro en ny typ av glidregel baserad på prosthaphaeresis , en algoritm för att snabbt beräkna produkter som går före logaritmer. Det har dock funnits lite praktiskt intresse för att konstruera en utöver den ursprungliga prototypen.

Specialiserade miniräknare

Glidregler har ofta specialiserats i varierande grad för sitt användningsområde, såsom punktskatter, bevisberäkning, ingenjörskonst, navigering etc., och vissa rutschbanor är extremt specialiserade för mycket snäva tillämpningar. Till exempel listar John Rabone & Sons 1892-katalogen ett "måttband och boskapsmätare", en anordning för att uppskatta vikten av en ko utifrån dess mått.

Det fanns många specialiserade diaregler för fotografiska applikationer. Till exempel aktinografen av Hurter och Driffield en enhet i buxbom, mässing och kartong med två diabilder för att uppskatta exponering från tid på dygnet, tid på året och breddgrad.

Specialiserade glidregler uppfanns för olika former av ingenjörskonst, affärer och bankverksamhet. Dessa hade ofta gemensamma beräkningar direkt uttryckta som specialskalor, till exempel lånekalkyler, optimala inköpskvantiteter eller speciella tekniska ekvationer. Till exempel Fisher Controls en anpassad skjutregel anpassad för att lösa ekvationerna som används för att välja rätt storlek på industriella flödeskontrollventiler.

Pilotballongglidregler användes av meteorologer inom vädertjänster för att bestämma de övre vindhastigheterna från en stigande väte- eller heliumfylld pilotballong.

E6 -B är en cirkulär linjal som används av piloter och navigatörer.

Cirkulära diaregler för att uppskatta ägglossningsdatum och fertilitet är kända som hjulräknare .

En publikation från försvarsdepartementet från 1962 inkluderade ökänt en cirkulär skjutregel för speciella ändamål för att beräkna sprängeffekter, övertryck och strålningsexponering från ett givet utbyte av en atombomb.

En E6-B flygdator
John Rabone & Sons 1892 boskapsmätare
Hurter och Driffields aktinograf
Kryptografisk skjutregel som användes av den schweiziska armén mellan 1914 och 1940

Nedgång

Den vetenskapliga kalkylatorn TI-30 , introducerades för under 25 USD 1976

Vikten av skjutregeln började minska när elektroniska datorer, en ny men sällsynt resurs på 1950-talet, blev mer allmänt tillgänglig för tekniska arbetare under 1960-talet.

Ett annat steg bort från bildreglerna var introduktionen av relativt billiga elektroniska vetenskapliga miniräknare. Den första inkluderade Wang Laboratories LOCI-2, som introducerades 1965, som använde logaritmer för multiplikation och division; och Hewlett-Packard HP 9100A , som introducerades 1968. Båda dessa var programmerbara och gav exponentiella och logaritmiska funktioner; HP hade trigonometriska funktioner (sinus, cosinus och tangent) och hyperboliska trigonometriska funktioner också. HP använde CORDIC- algoritmen (coordinate rotation digital computer), som möjliggör beräkning av trigonometriska funktioner med endast skift- och adderingsoperationer. Denna metod underlättade utvecklingen av allt mindre vetenskapliga miniräknare.

Precis som med stordatordatorer, påverkade inte tillgängligheten av dessa maskiner nämnvärt den allestädes närvarande användningen av skjutregeln förrän billiga handhållna vetenskapliga elektroniska miniräknare blev tillgängliga i mitten av 1970-talet, vid vilken tidpunkt den snabbt sjönk. Den vetenskapliga miniräknaren Hewlett-Packard HP-35 i fickstorlek var den första handhållna enheten av sitt slag, men den kostade 395 USD 1972. Detta var försvarligt för vissa ingenjörer, men för dyrt för de flesta studenter.

Runt 1974 gjorde den handhållna elektroniska vetenskapliga miniräknaren skjutreglerna i stort sett föråldrade. År 1975 kunde grundläggande elektroniska miniräknare med fyra funktioner köpas för mindre än $50, och 1976 såldes den vetenskapliga miniräknaren TI-30 för mindre än $25 ($119 justerat för inflation).

1980 var det sista året i Texas School UIL-tävling för att använda rutschbana. University Interscholastic League organiserades 1910. Ursprungligen bildades UIL för att administrera litterära evenemang, men blev också det styrande organet för skolidrottsevenemang.

Jämförelse med elektroniska digitala miniräknare

December 1951 reklam för IBM 604 Electronic Calculating Punch som uttryckligen jämför elektroniska datorer med ingenjörer som räknar med skjutregler

Inte ens under deras storhetstid slog rutschbanorna aldrig upp hos allmänheten. Addition och subtraktion är inte väl underbyggda operationer på diaregler och att göra en beräkning på en diaregel tenderar att vara långsammare än på en miniräknare. Detta ledde till att ingenjörer använde matematiska ekvationer som gynnade operationer som var lätta på en linjal framför mer exakta men komplexa funktioner; dessa approximationer kan leda till felaktigheter och misstag. Å andra sidan odlar den rumsliga, manuella manövreringen av skjutregler hos användaren en intuition för numeriska samband och skala som personer som enbart använt digitala miniräknare ofta saknar. En skjutregel kommer också att visa alla termer för en beräkning tillsammans med resultatet, vilket eliminerar osäkerheten om vilken beräkning som faktiskt utfördes.

En bildregel kräver att användaren separat beräknar storleksordningen på svaret för att placera decimalkomma i resultaten. Till exempel kommer 1,5 × 30 (vilket motsvarar 45) att visa samma resultat som 1 500 000 × 0,03 (vilket motsvarar 45 000). Denna separata beräkning tvingar användaren att hålla reda på storleken i korttidsminnet (vilket är felbenäget), föra anteckningar (vilket är krångligt) eller resonera om det i varje steg (vilket distraherar från de andra beräkningskraven).

Den typiska aritmetiska precisionen för en linjal är ungefär tre signifikanta siffror jämfört med många siffror på digitala miniräknare. Eftersom storleksordningen får störst framträdande plats när en bildregel används, är det mindre benägna att göra fel med falsk precision för användare .

När du utför en sekvens av multiplikationer eller divisioner med samma tal, kan svaret ofta bestämmas genom att bara titta på skjutregeln utan någon manipulation. Detta kan vara särskilt användbart när du beräknar procentsatser (t.ex. för testresultat) eller när du jämför priser (t.ex. i dollar per kilo). Flera hastighet-tid-avståndsberäkningar kan utföras handsfree med en blick med en linjal. Andra användbara linjära omvandlingar som pund till kilogram kan enkelt markeras på regeln och användas direkt i beräkningar.

Eftersom en linjal är helt mekanisk är den inte beroende av elnät eller batterier. Mekanisk oprecision i rutschbanor som var dåligt konstruerade eller skeva av värme eller användning kommer att leda till fel.

Många seglare har rutschbanor som backup för navigering i händelse av elfel eller batteritömning på långa sträckor. Slidregler används fortfarande ofta inom flyget, särskilt för mindre plan. De ersätts endast av integrerade, speciella och dyra flygdatorer, och inte miniräknare för allmänna ändamål. Den runda skjutregeln E6B som används av piloter har varit i kontinuerlig produktion och finns kvar i en mängd olika modeller. Vissa armbandsur som är designade för flyganvändning har fortfarande en linjalskala för att möjliggöra snabba beräkningar. Citizen Skyhawk AT och Seiko Flightmaster SNA411 är två anmärkningsvärda exempel.

Samtida användning

Faber-Castell linjal med påse

Även på 2000-talet föredrar vissa människor en skjutregel framför en elektronisk kalkylator som en praktisk datorenhet. Andra håller sina gamla rutschbanor borta från en känsla av nostalgi, eller samlar på dem som en hobby.

En populär samlarmodell är Keuffel & Esser Deci-Lon , en förstklassig vetenskaplig och teknisk skjutregel som finns både i en tio-tums (25 cm) "vanlig" ( Deci-Lon 10 ) och en fem-tums "ficka" ( Deci -Lon 5 ) variant. En annan uppskattad amerikansk modell är den åtta-tums (20 cm) Scientific Instruments cirkulära regeln. Av europeiska regler Faber-Castells exklusiva modeller de mest populära bland samlare.

Även om det cirkulerar väldigt många diaregler på marknaden, tenderar exemplar i gott skick att vara dyra. Många regler som hittats till försäljning på auktionssajter på nätet är skadade eller saknar delar, och säljaren kanske inte vet tillräckligt för att tillhandahålla relevant information. Reservdelar är få, dyra och i allmänhet tillgängliga endast för separat köp på enskilda samlares webbplatser. Keuffel- och Esser-reglerna från perioden fram till omkring 1950 är särskilt problematiska, eftersom ändstyckena på markörerna, gjorda av celluloid, tenderar att kemiskt brytas ner med tiden.

Det finns fortfarande en handfull källor för helt nya bildregler. The Concise Company of Tokyo, som började som tillverkare av cirkulära glidregler i juli 1954, fortsätter att tillverka och sälja dem idag. I september 2009 introducerade online-återförsäljaren ThinkGeek sitt eget märke av raka skjutregler, som beskrivs som "trogna replika[er]" som är "individuellt handverktyg". Dessa fanns inte längre tillgängliga under 2012. Dessutom hade Faber-Castell ett antal glidregler i lager, tillgängliga för internationellt köp via deras webbbutik, fram till mitten av 2018. Proportionhjul används fortfarande i grafisk design.

Olika appar för glidregelsimulator finns tillgängliga för Android- och iOS-baserade smarta telefoner och surfplattor.

Specialiserade rutschbanor som E6B som används inom flyget och skjutregler som används för att lägga artilleri används fortfarande men inte längre rutinmässigt. Dessa regler används som en del av undervisnings- och instruktionsprocessen då eleven i att lära sig använda dem också lär sig om principerna bakom beräkningarna, det gör det också möjligt för eleven att kunna använda dessa instrument som backup i händelse av att den moderna elektronik i allmänt bruk misslyckas.

Samlingar

En stor linjal som visas på MIT Museum

MIT Museum i Cambridge, Massachusetts , har en samling av hundratals skjutregler, nomogram och mekaniska miniräknare . Keuffel and Esser Company-samlingen, från tillverkaren av skjutregeln som tidigare låg i Brooklyn, New York , donerades till MIT omkring 2005. Utvalda föremål från samlingen visas vanligtvis på museet.

International Slide Rule Museum sägs vara "[världens] mest omfattande resurs för allt som rör glidregler och logaritmiska miniräknare". Museets webbsida innehåller litteratur om bildregler i avsnittet "Slide Rule Library".

Se även

Kulram
Flygdator
Flytpunkt
Hans Peter Luhn , uppfinnare av Lunometern, en trådräknare
Nomogram
Sektor (instrument)
Bilddiagram
Tidslinje för datoranvändning
Vernier skala
Volelle

Anteckningar

externa länkar

Allmän information, historia

International Slide Rule Museum
Historien, teorin och användningen av den tekniska glidregeln - Av Dr James B. Calvert, University of Denver
Storbritannien Slide Rule Circle Hemsida
Oughtred Society Slide Rule Hemsida — Dedikerad till bevarandet och historien om slide-regler
Rod Lovett's Slide Rules – Omfattande Aristo-sajt med många sökmöjligheter
Dereks virtuella bildregelgalleri — Javascript-simuleringar av historiska bildregler
"Glidregel" . New International Encyclopedia . 1905.
"Slide-regel" . Encyclopedia Americana . 1920.
Reglas de Cálculo — En mycket stor Faber Castell-kollektion
Samling av rutschbanor - franska rutschbanor (Graphoplex, Tavernier-Gravet och andra)
Eric's Slide Rule Site — Historik och användning
Bildregler — Information från Museum of HP Calculators
Beskrivningar, alfabetiskt efter varumärke, med bilder (Vintage Tech. Assoc.)