Asymptotisk förstärkningsmodell

Den asymptotiska förstärkningsmodellen (även känd som Rosenstark-metoden ) är en representation av förstärkningen av negativ återkopplingsförstärkare som ges av den asymptotiska förstärkningsrelationen:

$G=G_{\infty }\left({\frac {T}{T+1}}\right)+G_{ 0}\left({\frac {1}{T+1}}\right)\ ,$

där $T$ är returförhållandet med ingångskällan inaktiverad (lika med det negativa av loopförstärkningen i fallet med ett enkelloopsystem som består av unilaterala block), G _∞ är den asymptotiska förstärkningen och G ₀ är direkt sändningstid. Denna form för förstärkningen kan ge intuitiv insikt i kretsen och är ofta lättare att härleda än en direkt attack på förstärkningen.

Figur 1: Blockdiagram för asymptotisk förstärkningsmodell

Figur 1 visar ett blockschema som leder till det asymptotiska förstärkningsuttrycket. Den asymptotiska förstärkningsrelationen kan också uttryckas som en signalflödesgraf . Se figur 2. Den asymptotiska förstärkningsmodellen är ett specialfall av extraelementsatsen .

Figur 2: Möjligt ekvivalent signalflödesdiagram för den asymptotiska förstärkningsmodellen

Som direkt följer av begränsande fall av förstärkningsuttrycket är den asymptotiska förstärkningen G _∞ helt enkelt systemets förstärkning när returförhållandet närmar sig oändligheten:

$G_{\infty }=G\ {\Big |}_{T\rightarrow \infty }\ ,$

medan den direkta överföringstermen G ₀ är förstärkningen av systemet när returförhållandet är noll:

$G_{0}=G\ {\Big |}_{T\rightarrow 0}\ .$

Fördelar

• Denna modell är användbar eftersom den helt karakteriserar återkopplingsförstärkare, inklusive laddningseffekter och de bilaterala egenskaperna hos förstärkare och återkopplingsnätverk.
• Ofta är återkopplingsförstärkare utformade så att returförhållandet T är mycket större än ett. I detta fall, och om man antar att den direkta överföringstermen G är liten (som den ofta är) ₀ , är systemets förstärkning G ungefär lika med den asymptotiska förstärkningen G _∞ .
• Den asymptotiska förstärkningen är (vanligtvis) endast en funktion av passiva element i en krets, och kan ofta hittas genom inspektion.
• Återkopplingstopologin (serie-serie, serie-shunt, etc.) behöver inte identifieras i förväg eftersom analysen är densamma i alla fall.

Genomförande

Direkt tillämpning av modellen innebär följande steg:

1. Välj en beroende källa i kretsen.
2. Hitta returförhållandet för den källan.
3. Hitta förstärkningen G _∞ direkt från kretsen genom att ersätta kretsen med en motsvarande T = ∞.
4. Hitta förstärkningen G ₀ direkt från kretsen genom att ersätta kretsen med en motsvarande T = 0.
5. Ersätt värdena för T, G _∞ och G ₀ med formeln för asymptotisk förstärkning.

Dessa steg kan implementeras direkt i SPICE med hjälp av småsignalkretsen för handanalys. I detta tillvägagångssätt är de beroende källorna för anordningarna lätt åtkomliga. Däremot, för experimentella mätningar med verkliga enheter eller SPICE-simuleringar med numeriskt genererade enhetsmodeller med otillgängliga beroende källor, kräver utvärdering av returförhållandet speciella metoder .

Samband med klassisk feedbackteori

₀ Klassisk feedbackteori försummar feedforward ( G ). Om feedforward tappas blir förstärkningen från den asymptotiska förstärkningsmodellen

$G=G_{\infty }{\frac {T}{1+T}}={\frac {G_{ \infty }T}{1+{\frac {1}{G_{\infty }}}G_{\infty }T}}\ ,$

medan i klassisk återkopplingsteori, i termer av öppen loop-förstärkning A , är förstärkningen med återkoppling (förstärkning med sluten loop):

$A_{\mathrm {FB} }={\frac {A}{1+{\beta }_{\mathrm {FB} }A}}\ .$

Jämförelse av de två uttrycken indikerar att återkopplingsfaktorn β _FB är:

$\beta _{\mathrm {FB} }={\frac {1}{G_{\infty }}}\ ,$

medan förstärkningen med öppen slinga är:

$A=G_{\infty }\ T\ .$

Om noggrannheten är tillräcklig (vanligtvis är det det), föreslår dessa formler en alternativ utvärdering av T : utvärdera den öppna slingaförstärkningen och G _∞ och använd dessa uttryck för att hitta T . Ofta är dessa två utvärderingar lättare än utvärdering av T direkt.

Exempel

Stegen för att härleda förstärkningen med den asymptotiska förstärkningsformeln beskrivs nedan för två negativ återkopplingsförstärkare. Exemplet med en transistor visar hur metoden fungerar i princip för en transkonduktansförstärkare, medan det andra exemplet med två transistorer visar tillvägagångssättet för mer komplexa fall med en strömförstärkare.

Enstegs transistorförstärkare

Figur 3: FET-återkopplingsförstärkare

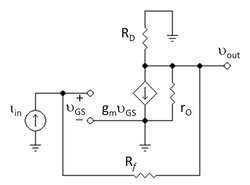
Betrakta den enkla FET- återkopplingsförstärkaren i figur 3. Syftet är att hitta den lågfrekventa, öppen krets, transresistansförstärkningen för denna krets G = v _ut / i _med användning av den asymptotiska förstärkningsmodellen.

Figur 4: Småsignalkrets för transresistansförstärkare; återkopplingsmotståndet Rf placeras under förstärkaren för _att likna standardtopologin

Figur 5: Småsignalkrets med bruten returbana och testspänningsdrivande förstärkare vid avbrottet

Den ekvivalenta kretsen med liten signal visas i figur 4, där transistorn ersätts av sin hybrid-pi-modell .

Returförhållande

Det är enklast att börja med att hitta returförhållandet T , eftersom G ₀ och G _∞ definieras som begränsande former av förstärkningen eftersom T tenderar mot antingen noll eller oändligt. För att ta dessa gränser är det nödvändigt att veta vilka parametrar T beror på. Det finns bara en beroende källa i denna krets, så som utgångspunkt bestäms avkastningsförhållandet som är relaterat till denna källa enligt artikeln om avkastningsförhållande .

Returförhållandet hittas med hjälp av figur 5. I figur 5 är ingångsströmkällan inställd på noll. Genom att skära ut den beroende källan från kretsens utgångssida och kortsluta dess terminaler, är kretsens utgångssida isolerad från ingången och återkopplingsslingan bryts. En testström i _t ersätter den beroende källan. Därefter hittas returströmmen som genereras i den beroende källan av testströmmen. Returförhållandet är då T = − i _r / i _t . Genom att använda denna metod och notera att R D _är parallell med r _O bestäms T som:

$T=g_{\mathrm {m} }\left(R_{\mathrm {D} }\ ||r_{\mathrm { O} }\right)\approx g_{\mathrm {m} }R_{\mathrm {D} }\ ,$

där approximationen är korrekt i det vanliga fallet där r _O >> R _D . Med detta samband är det tydligt att gränserna T → 0, eller ∞ realiseras om vi låter transkonduktansen g _m → 0, eller ∞.

Asymptotisk vinst

Att hitta den asymptotiska förstärkningen G _∞ ger insikt och kan vanligtvis göras genom inspektion. För att hitta G _∞ låter vi g _m → ∞ och hitta den resulterande förstärkningen. Drainströmmen, i _D = g _m v _GS , måste vara ändlig. Därför, när g _m närmar sig oändligheten, måste v _GS också närma sig noll. Eftersom källan är jordad, innebär v _{GS = 0} v _G = 0 också. Med v _G = 0 och det faktum att all ingångsström flyter genom Rf (eftersom FET har _en oändlig ingångsimpedans), är utspänningen helt enkelt ₋ i _i Rf . Därav

$G_{\infty }={\frac {v_{\mathrm {out} }}{i_{\mathrm {in} }}}=-R_{\mathrm {f} }\ .$

Alternativt är G∞ _en den förstärkning som hittas genom att ersätta transistorn med en ideal förstärkare med oändlig förstärkning - noll .

Direkt genommatning

För att hitta den direkta genomströmningen $G_{0}$ låter vi helt enkelt g _m → 0 och beräknar den resulterande förstärkningen. Strömmarna genom Rf och den parallella kombinationen _av R _D || r _O måste därför vara samma och lika med i _i . Utspänningen är därför i _in (RD _|| r _O ) .

Därav

$G_{0}={\frac {v_{out}}{i_{in}}}=R_{D}\| r_{O}\approx R_{D}\ ,$

där approximationen är korrekt i det vanliga fallet där r _O >> R _D .

Total vinst

Den totala transresistansförstärkningen för denna förstärkare är därför:

$G={\frac {v_{out}}{i_{in}}}=-R_{f}{\frac {g_{m}R_{D}}{1+g_{m}R_{D }}}+R_{D}{\frac {1}{1+g_{m}R_{D}}}={\frac {R_{D}\left(1-g_{m}R_{f}\ höger)}{1+g_{m}R_{D}}}\ .$

Genom att undersöka denna ekvation verkar det vara fördelaktigt att göra R _D stor för att få den totala förstärkningen att närma sig den asymptotiska förstärkningen, vilket gör förstärkningen okänslig för förstärkarparametrar RD ₍ gm _. och ) Dessutom minskar en stor första term vikten av den direkta genomströmningsfaktorn, vilket försämrar förstärkaren. Ett sätt att öka R _D är att ersätta detta motstånd med en aktiv belastning , till exempel en strömspegel .

Figur 6: Återkopplingsförstärkare med två transistorer; valfri källimpedans R _S klumpas ihop med basmotståndet RB _.

Tvåstegs transistorförstärkare

Figur 7: Schema för användning av en asymptotisk förstärkningsmodell; parameter α = β/(β+1); motstånd _RC = _RC1 .

visar en tvåtransistorförstärkare med ett återkopplingsmotstånd Rf _. Denna förstärkare hänvisas ofta till som en Rf är i shunt (parallell _{återkopplingsförstärkare} i shuntserie och analyseras utifrån att motståndet R2 ₎ är i serie med utgången och samplar utströmmen, medan med ingången och subtraherar från ingångsström. Se artikeln om negativ återkopplingsförstärkare och referenser av Meyer eller Sedra. Det vill säga att förstärkaren använder strömåterkoppling. Det är ofta tvetydigt vilken typ av återkoppling som är involverad i en förstärkare, och den asymptotiska förstärkningsmetoden har fördelen/nackdelen att den fungerar oavsett om du förstår kretsen eller inte.

Figur 6 anger utgångsnoden, men anger inte valet av utgångsvariabel. I det följande väljs utgångsvariabeln som kortslutningsström för förstärkaren, det vill säga kollektorströmmen för utgångstransistorn. Andra val för utdata diskuteras senare.

För att implementera den asymptotiska förstärkningsmodellen kan den beroende källan associerad med endera transistorn användas. Här väljs den första transistorn.

Returförhållande

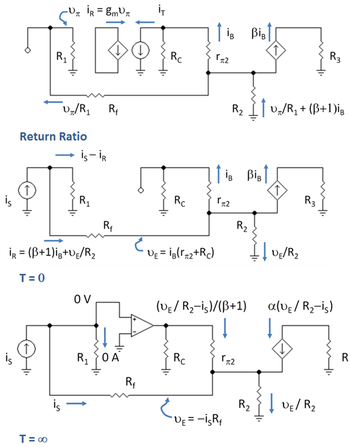
Kretsen för att bestämma returförhållandet visas i den övre panelen i figur 7. Etiketter visar strömmarna i de olika grenarna som hittats med en kombination av Ohms lag och Kirchhoffs lagar . Motstånd R1 = R _B //r π1 _och R3 = R _{C2 //} R _{L .} KVL från grunden för R ₁ till grunden för R ₂ ger:

$i_{\mathrm {B} }=-v_{\pi }{\frac {1+R_{2}/R_{1}+R_{\mathrm {f} }/R_{1}}{( \beta +1)R_{2}}}\ .$

tillhandahåller kollektorspänningen överst på RC _as

$v_{\mathrm {C} }=v_{\pi }\left(1+{\frac {R_{\mathrm {f} }}{R_{1}}}\right)-i_{\mathrm {B} }r_{\pi 2}\ .$

Slutligen ger KCL på denna samlare

$i_{\mathrm {T} }=i_{\mathrm {B} }-{\frac {v_{\mathrm {C} }}{R_{\mathrm {C} }}}\ .$

Genom att ersätta den första ekvationen med den andra och den andra med den tredje, återfinns avkastningsförhållandet som

$}}$$T=-{\frac {i_{\mathrm {R} }}{i_{\mathrm {T} }}}=-g_{\ mathrm {m} }{\frac {v_{\pi }$

$={\frac {g_{\mathrm {m} }R_{\mathrm {C} }}{\left(1+{\frac {R_{\mathrm {f} }}{R_{1}} }\right)\left(1+{\frac {R_{\mathrm {C} }+r_{\pi 2}}{(\beta +1)R_{2}}}\right)+{\frac { R_{\mathrm {C} }+r_{\pi 2}}{(\beta +1)R_{1}}}}}\ .$

Få G ₀ med T = 0

Kretsen för att bestämma G ₀ visas i mittpanelen i figur 7. I figur 7 är utgångsvariabeln utströmmen β i _B (kortslutningsbelastningsströmmen), vilket leder till kortslutningsströmförstärkningen för förstärkaren , nämligen β i _B / i _S :

$G_{0}={\frac {\beta i_{B}}{i_{S}}}\ .$

Med hjälp av Ohms lag hittas spänningen överst på R _{1 som}

$(i_{S}-i_{R})R_{1}=i_{R}R_{f}+v_{E} \ \ ,$

eller, ordna om termer,

$i_{S}=i_{R}\left(1+{\frac {R_{f}}{R_{1}}}\right)+{\frac {v_{E}}{R_{1 }}}\ .$

Använder KCL överst i R ₂ :

$i_{R}={\frac {v_{E}}{R_{2}}}+(\beta +1)i_{B}\ .$

Emitterspänningen v _E iS _är redan känd i termer av iB _, och _från diagrammet i figur 7. Genom att ersätta den andra ekvationen i den första, bestäms iB endast i termer av G blir ₀ :

$G_{0$

Vinst G ₀ representerar feedforward genom återkopplingsnätverket och är vanligtvis försumbar.

Få G _∞ med T → ∞

Kretsen för att bestämma G _∞ visas i den nedre panelen i figur 7. Introduktionen av den ideala op-förstärkaren (en nullor ) i denna krets förklaras enligt följande. När T → ∞ går förstärkarens förstärkning till oändlighet också, och i ett sådant fall drivs differentialspänningen som driver förstärkaren (spänningen över ingångstransistorn r π1 ) till _{noll och (enligt Ohms lag när det finns} ingen spänning) drar den ingen inström. Å andra sidan är utströmmen och utspänningen vad kretsen kräver. Detta beteende är som en nollor, så en nollor kan införas för att representera transistorn med oändlig förstärkning.

Strömförstärkningen läses direkt från schemat:

$G_{\infty }={\frac {\beta i_{B}}{i_{S}}}=\left({\frac {\beta }{\beta +1}}\right)\left (1+{\frac {R_{f}}{R_{2}}}\höger)\ .$

Jämförelse med klassisk feedbackteori

Med den klassiska modellen försummas framkopplingen och återkopplingsfaktorn β _FB är (förutsatt att transistorn β >> 1):

$\beta _{FB}={\frac {1}{G_{\infty } }}\approx {\frac {1}{(1+{\frac {R_{f}}{R_{2}}})}}={\frac {R_{2}}{(R_{f}+ R_{2})}}\ ,$

och förstärkningen A med öppen slinga är:

$A=G_{\infty }T\approx {\frac {\left(1+{\frac {R_{f}}{R_{2}}}\right)g_{m}R_{C}} {\left(1+{\frac {R_{f}}{R_{1}}}\right)\left(1+{\frac {R_{C}+r_{\pi 2}}{(\beta +1)R_{2}}}\right)+{\frac {R_{C}+r_{\pi 2}}{(\beta +1)R_{1}}}}}\ .$

Total vinst

Ovanstående uttryck kan ersättas med den asymptotiska förstärkningsmodellekvationen för att hitta den totala förstärkningen G. Den resulterande förstärkningen är strömförstärkningen för förstärkaren med en kortslutningsbelastning.

Vinst med alternativa utdatavariabler

I förstärkaren i figur 6 är RL och RC2 _{parallella .} För att erhålla transresistansförstärkningen, säg A _{ρ , det vill säga förstärkningen med spänning som utgångsvariabel,} multipliceras kortslutningsströmförstärkningen G med R _C2 // R _L i enlighet med Ohms lag :

$A_{\rho }=G\left(R_{\mathrm {C2} }//R_{\mathrm {L} }\right)\ .$

Spänningsförstärkningen för öppen krets hittas från A _ρ genom att ställa in RL → ∞ _.

För att erhålla strömförstärkningen när belastningsström i _L i belastningsmotstånd R _L är utgångsvariabeln, säg A _{i ,} används formeln för strömdelning : i _L = i _ut × R _C2 / ( R _C2 + R _L ) och kortslutningsströmförstärkningen G multipliceras med denna belastningsfaktor :

$A_{i}=G\left({\frac {R_{C2}}{R_{C2}+R_{L}}}\right)\ .$

Naturligtvis återvinns kortslutningsströmförstärkningen genom att sätta R _L = 0 Ω.

Se även

• Blackmans teorem
• Extra elementsats
• Mason's gain formel
• Återkopplingsförstärkare
• Returförhållande
• Signalflödesgraf

externa länkar

• Föreläsningsanteckningar om den asymptotiska förstärkningsmodellen