Mason's gain formel

Masons förstärkningsformel (MGF) är en metod för att hitta överföringsfunktionen för en linjär signalflödesgraf ( SFG). Formeln härleddes av Samuel Jefferson Mason , som den också är uppkallad efter. MGF är en alternativ metod för att hitta överföringsfunktionen algebraiskt genom att märka varje signal, skriva ner ekvationen för hur den signalen beror på andra signaler och sedan lösa de multipla ekvationerna för utsignalen i termer av insignalen. MGF tillhandahåller en steg-för-steg-metod för att erhålla överföringsfunktionen från en SFG. Ofta kan MGF bestämmas genom inspektion av SFG. Metoden kan enkelt hantera SFG med många variabler och loopar inklusive loopar med inre loopar. MGF kommer ofta upp i samband med styrsystem , mikrovågskretsar och digitala filter eftersom dessa ofta representeras av SFG.

Formel

Förstärkningsformeln är följande:

G={\frac {y_{\text{out}}}{y_{\text{in}}}}={\frac {\summa _{k=1}^{N}{G_{k}\Delta _{k}}}{\Delta \ }}

\Delta =1-\summa L_{i}+\summa L_{i}L_{j}-\summa L_{i}L_{ j}L_{k}+\cdots +(-1)^{m}\sum \cdots +\cdots

var:

Δ = determinanten för grafen.
y _in = input-nod variabel
y _ut = output-nod variabel
G = fullständig förstärkning mellan y _in och y _out
N = totalt antal framåtvägar mellan y _in och y _ut
G _k = banförstärkning för den k: te framåtriktade banan mellan y _in och y _ut
Li ₌ slingförstärkning för varje sluten slinga i systemet
L _i L _j = produkten av slingförstärkningarna för två valfria slingor (inga gemensamma noder)
L _i L _j L _k = produkten av slingförstärkningarna för tre parvisa icke-berörande slingor
Δk = kofaktorvärdet för Δ för den k: ^te framåtriktade banan, med slingorna som rör vid den k: _te^{framåtriktade} banan borttagna. *

Definitioner

Bana: en kontinuerlig uppsättning grenar som korsas i den riktning som de anger.
Framåtväg: En väg från en ingångsnod till en utgångsnod där ingen nod berörs mer än en gång.
Loop: En bana som börjar och slutar på samma nod där ingen nod berörs mer än en gång.
Banvinst: produkten av vinsterna för alla grenar i banan.
Loop gain: produkten av förstärkningarna av alla grenar i loopen.

Procedur för att hitta lösningen

Gör en lista över alla framåtriktade banor och deras vinster, och märk dessa G _k .
Gör en lista över alla slingor och deras förstärkningar och märk dessa L _i (för i- slingor). Gör en lista över alla par av icke-berörande slingor och produkterna av deras vinster ( L _i L _j ). Gör en lista över alla parvisa icke-berörande slingor tagna tre åt gången ( L _i L _j L _k ), sedan fyra åt gången, och så vidare, tills det inte finns fler.
Beräkna determinanten Δ och kofaktorerna Δ _k .
Använd formeln.

Exempel

Krets som innehåller två-portar

Signalflödesdiagram för en krets som innehåller två portar. Vägen framåt från ingång till utgång visas i en annan färg.

Överföringsfunktionen från V _in till V ₂ önskas.

Det finns bara en väg framåt:

V _in till V ₁ till I ₂ till V ₂ med förstärkning $G_{1}=-y_{21}R_{L}\,$

Det finns tre slingor:

V ₁ till I ₁ till V ₁ med förstärkning $L_{1}=-R_{\text{in}}y_{11}\,$
V ₂ till I ₂ till V ₂ med förstärkning $L_{2}=-R_{L}y_{22}\,$
V ₁ till I ₂ till V ₂ till I ₁ till V ₁ med förstärkning $L_{3}=y_{21}R_{L}y_{12}R_{\ text{i}}\,$

\Delta =1-(L_{1}+L_{2}+L_{3})+(L_{1 }L_{2})\,

notera: L ₁ och L ₂ berör inte varandra medan L ₃ berör båda de andra slingorna.

\Delta _{1}=1\,

notera: den framåtriktade banan berör alla slingor så allt som är kvar är 1 .

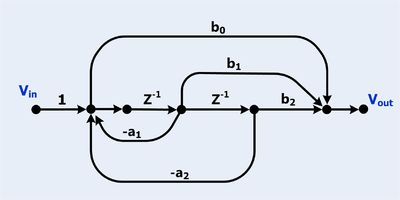
G={\frac {G_{1}\Delta _{1}}{\Delta }}={\frac {-y_{21}R_{L}}{1+R_{\text{in}}y_{11}+R_{ L}y_{22}-y_{21}R_{L}y_{12}R_{\text{in}}+R_{\text{in}}y_{11}R_{L}y_{22}}} \,

Digitalt IIR biquad-filter

Signalflödesdiagrammet (SFG) för ett digitalt bi-quad-filter med oändlig impulssvar. Denna SFG har tre framåtriktade banor och två slingor.

Digitala filter är ofta ritade som signalflödesdiagram.

Det finns två slingor

$L_{1}=-a_{1}Z^{-1}\,$
$L_{2}=-a_{2}Z^{-2}\,$

\Delta =1-(L_{1}+L_{2})\,

Observera att de två slingorna berör varandra så det finns ingen term för deras produkt.

Det finns tre vägar framåt

$G_{0}=b_{0}\,$
$G_{1}=b_{1}Z^{-1}\,$
$G_{2}=b_{2}Z^{-2}\,$

Alla framåtriktade banor berör alla slingor så

\Delta _{0}=\Delta _{1}=\Delta _{2}=1\,

G={\frac {G_{0}\Delta _{0}+G_{1}\Delta _{1}+G_{2}\Delta _{ 2}}{\Delta }}\,

G={\frac {b_{ 0}+b_{1}Z^{-1}+b_{2}Z^{-2}}{1+a_{1}Z^{-1}+a_{2}Z^{-2}} }\,

Servo

Vinkelpositionsservo och signalflödesgraf. θ _C = önskad vinkelkommando, θ _L = faktisk belastningsvinkel, K _P = positionsslingans förstärkning, V _{ω C} = hastighetskommando, V _ωM = motorhastighetsavkänningsspänning, K _V = hastighetsslingans förstärkning, V _IC = strömkommando, V _IM = strömavkänningsspänning, K _C = strömslingförstärkning, VA = effektförstärkarens utspänning, _V M ₌ effektiv spänning över induktansen, L _M = motorinduktans, _IM = motorström, R _M = motorresistans, R _S = strömavkänningsresistans, K _M = motormomentkonstant ( Nm /amp), T = vridmoment, M = tröghetsmoment för alla roterande komponenter α = vinkelacceleration, ω = vinkelhastighet, β = mekanisk dämpning, GM = _motorns baksida EMF-konstant, G _T = varvräknarens omvandlingsförstärkningskonstant. Det finns en framåtriktad väg (visas i en annan färg) och sex återkopplingsslingor. Drivaxeln antogs vara tillräckligt styv för att inte behandlas som en fjäder. Konstanter visas i svart och variabler i lila.

Signalflödesdiagrammet har sex slingor. Dom är:

$L_{0}=-{\frac {\beta }{sM}}\,$

$L_{1} ={\frac {-(R_{M}+R_{S})}{sL_{M}}}\,$

${\displaystyle L_{2}=\ ,{\frac {-G_{M}K_{M}}{s^{2}L_{M}M}}} L$

$\displaystyle L_{3}={\ frac {-K_{C}R_{S}}{sL_{M}}}\,}$

$L_{4}={\frac {-K_{V}K_{C}K_{M}G_{T}}{s^{2}L_{M}M}}\,$

$L_{5}={\frac {-K_{P}K_{V}K_{C}K_{M}}{s^{3}L_{M}}\,$

\Delta =1-(L_{0}+L_{1}+L_ {2}+L_{3}+L_{4}+L_{5})+(L_{0}L_{1}+L_{0}L_{3})\,

Det finns en väg framåt:

$g_{0}={\frac {K_{P}K_{V}K_{C}K_{M}}{s^{3} L_{M}M}}\,$

Den framåtriktade banan berör alla slingor och därför är kofaktorn $\Delta _{0}=1$

Och förstärkningen från ingång till utgång är ${\frac {\theta _{L}}{\theta _{C}}}={\frac {g_{0}\Delta _{0}}{\Delta }}\,$

Motsvarande matrisform

Mason's regel kan anges i en enkel matrisform. Antag att $\mathbf {T}$ är den transienta matrisen för grafen där $t_{nm}=\left[\mathbf {T} \right]_{nm }$ är summatransmittansen av grenar från nod m mot nod n . Sedan är förstärkningen från nod m till nod n i grafen lika med $u_{nm}=\left[\mathbf {U} \right]_{nm}$ , var

\mathbf {U} =\left(\mathbf {I} -\mathbf {T} \right)^{-1}

,

och $\mathbf {I}$ är identitetsmatrisen.

Mason's Rule är också särskilt användbar för att härleda z-domänöverföringsfunktionen för diskreta nätverk som har inre återkopplingsslingor inbäddade i yttre återkopplingsslingor (kapslade loopar). Om det diskreta nätverket kan ritas som en signalflödesgraf, kommer tillämpningen av Masons regel att ge det nätverkets z-domän H(z) överföringsfunktion.

Komplexitet och beräkningstillämpningar

Mason's Rule kan växa faktoriellt, eftersom uppräkningen av banor i en riktad graf växer dramatiskt. För att se detta överväga den fullständiga riktade grafen på $n$ hörn, med en kant mellan varje par av hörn. Det finns en sökväg från $y_{\text{in}}$ till $y_{\text{out}}$ för var och en av $(n-2)!$ permutationer av de mellanliggande hörnen. Således Gaussisk eliminering mer effektiv i det allmänna fallet.

Ändå karakteriserar Masons regel överföringsfunktionerna för sammankopplade system på ett sätt som samtidigt är algebraiskt och kombinatoriskt, vilket möjliggör allmänna påståenden och andra beräkningar i algebraisk systemteori. Medan många inverser inträffar under Gaussisk eliminering, samlar Masons regel naturligtvis dessa till en enda kvasi-invers . Allmän form är

{\frac {p}{1-q}},

Där som beskrivits ovan är $q$ en summa av cykelprodukter, som var och en typiskt faller in i ett ideal (till exempel de strikt kausala operatorerna). Bråk av denna form gör en subring $R(1+\langle L_{i}\rangle )^{-1}$ av det rationella funktionsfältet . Denna observation överförs till det icke-kommutativa fallet, även om själva Masons regel då måste ersättas av Riegles regel .

Se även

Anteckningar

Bolton, W. Newnes (1998). Control Engineering Pocketbook . Oxford: Newnes.
Van Valkenburg, ME (1974). Nätverksanalys (3:e upplagan). Englewood Cliffs, NJ: Prentice-Hall.