Vitali som täcker lemma

Inom matematik är Vitalis täckande lemma ett kombinatoriskt och geometriskt resultat som vanligtvis används i måttteorin för euklidiska rum . Detta lemma är ett mellanliggande steg, av oberoende intresse, i beviset för Vitali-täckningssatsen . Den täckande satsen krediteras den italienske matematikern Giuseppe Vitali . Satsen anger att det är möjligt att täcka, upp till en Lebesgue-försumbar mängd , en given delmängd E av R ^d av en osammanhängande familj extraherad från en Vitali-täckning av E .

Vitali som täcker lemma

Visualisering av lemma i $\mathbb {R} ^{1}$ .

På toppen: en samling bollar; de gröna bollarna är den osammanhängande undersamlingen. På botten: undersamlingen med tre gånger radien täcker alla bollar.

Det finns två grundläggande versioner av lemma, en finit version och en oändlig version. Båda lemman kan bevisas i den allmänna inställningen av ett metriskt utrymme , vanligtvis tillämpas dessa resultat på specialfallet med det euklidiska rummet $\mathbb {R} ^{d}$ . I båda satserna kommer vi att använda följande notation: om ${\textstyle B=B(x,r)}$ är en boll och $c\in \mathbb {R}$ , kommer vi att skriva $cB$ för bollen ${\textstyle B(x,cr)}$ .

Finit version

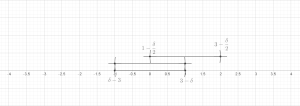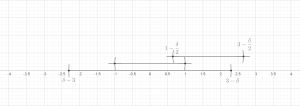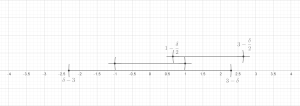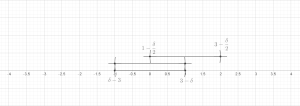
Sats (Finite Covering Lemma). Låt $B_{1},\dots ,B_{n}$ vara vilken ändlig samling bollar som helst i ett godtyckligt metriskt utrymme. Sedan finns det en undersamling $B_{j_{1}},B_{j_{2}},\dots ,B_{j_{m}}$ av dessa bollar som är osammanhängande och tillfredsställer

$$B_{1}\cup B_{2}\cup \dots \cup B_{n}\subseteq 3B_{j_{1}}\cup 3B_{j_{2}}\cup \dots \cup 3B_{j_ {m}}.$$

Bevis: Utan förlust av allmänhet antar vi att samlingen av bollar inte är tom; det vill säga n > 0. Låt $B_{j_{1}}$ vara kulan med största radie. Antag induktivt att $B_{j_{1}},\dots ,B_{j_{k}}$ har valts. Om det finns någon boll i $B_{1},\dots ,B_{n}$ som är disjunkt från ${\displaystyle B_ {j_{1}}\cup B_{j_{2}}\cup \dots \cup B_{j_{k}}} ,$ låt $B_{j_{k+1}}$ vara sådan boll med maximal radie (bryter band godtyckligt), annars sätter vi m := k och avslutar den induktiva definitionen.

Ställ nu in ${\textstyle X:=\bigcup _{k=1}^{m}3\,B_{j_{k}}}$ . Det återstår att visa att $B_{i}\subset X$ för varje $i=1,2,\dots ,n$ . Detta är tydligt om $i\in \{j_{1},\dots ,j_{m}\}$ . Annars finns det nödvändigtvis några $k\in \{1,\dots ,m\}$ så att $B_{i}$ skär ${\ displaystyle B_{j_{k}}}$ och radien för $B_{j_{k}}$ är minst lika stor som den för $B_{i}$ . Triangelolikheten innebär då lätt att ${\displaystyle B_{i}\delmängd 3\,B_{j_{k}}\delmängd X} ,$ efter behov. Detta avslutar beviset för den finita versionen.

Oändlig version

Teorem (oändligt täckande lemma). Låt $\mathbf {F}$ vara en godtycklig samling bollar i ett separerbart metriskt utrymme så att

$$R:=\sup \,\{\mathrm {rad} (B):B\in \mathbf {F} \}< \infty$$

där $\mathrm {rad} (B)$ anger kulans B . Sedan finns det en räknebar undersamling $\mathbf {G} \subset \mathbf {F}$ så att kulorna i $\mathbf {G}$ är parvis disjunkta och uppfyller

$$\bigcup _{B\in \mathbf {F} }B\subseteq \bigcup _{C\in \mathbf {G} }5\,C.$$

Och dessutom skär varje $B\in \mathbf {F}$ några $C\in \mathbf {G}$ med $B\subset 5C$ .

Bevis: Betrakta uppdelningen av F i undersamlingar F _n , n ≥ 0, definierad av

$\mathbf {F} _{n}=\{B\in \mathbf {F} :2^{-n-1}R<{\text{rad}}(B)\leq 2^{- n}R\}.$

₀₀₀₀₀ Det vill säga ${\textstyle \mathbf {F} _{n}}$ består av kulorna B vars radie är i (2 ^{− n −1} R , 2 ^{− n} R ]. En sekvens G _n , med G _n ⊂ F _n , definieras induktivt enligt följande: Sätt först H = F och låt G vara en maximal disjunkt delsamling av H (en sådan delsamling existerar enligt Zorns lemma ) Om vi ​​antar att G ,..., G _n har valts, låt

$\mathbf {H} _{n+1}=\{ B\in \mathbf {F} _{n+1}:\ B\cap C=\emptyset ,\ \ \forall C\in \mathbf {G} _{0}\cup \mathbf {G} _{1 }\cup \dots \cup \mathbf {G} _{n}\},$

och låt Gn _{. +1 vara en maximal} disjunkt subsamling av Hn _{+ 1} Underkollektionen

$\mathbf {G} :=\bigcup _{n=0}^{\infty }\mathbf {G} _{n}$

₀₀ av F uppfyller kraven för satsen: G är en disjunkt samling, och är således räknebar eftersom det givna metriska utrymmet är separerbart. Dessutom skär varje kula B ∈ F en boll C ∈ G så att B ⊂ 5 C . Faktum är att om vi får några ${\displaystyle B\in \mathbf {F} } ,$ måste det finnas några n vara sådana att B tillhör F _n . Antingen tillhör B inte H _n , vilket innebär n > 0 och betyder att B skär en boll från föreningen av G , …, G _{n −1} , eller B ∈ H _n och genom maximalitet av G _n skär B en boll i Gn . _{_} I alla fall skär B en kula C som tillhör föreningen av G , …, G _n . En sådan kula C måste ha en radie som är större än 2 ^{− n −1} R . Eftersom radien för B är mindre än eller lika med 2 ^{− n} R, kan vi dra slutsatsen med triangelolikheten att B ⊂ 5 C, som påståtts. Från detta $\bigcup _{B\in \mathbf {F} }B\subseteq \bigcup _{C\in \mathbf {G} }5\,C$ följer omedelbart och avslutar beviset.

Anmärkningar

• I den oändliga versionen kan den första samlingen av bollar vara räknebara eller oräkneliga . I ett separerbart metriskt utrymme måste varje parvis osammanhängande samling av bollar kunna räknas. I ett icke-separerbart utrymme visar samma argument att det finns en parvis osammanhängande underfamilj, men den familjen behöver inte kunna räknas.
• Resultatet kan misslyckas om radierna inte är begränsade: betrakta familjen av alla kulor centrerade vid 0 i R ^d ; någon osammanhängande underfamilj består av endast en boll B och 5 B innehåller inte alla bollar i denna familj.
• Konstanten 5 är inte optimal. Om skalan c ^{− n} , c > 1, används istället för 2 ^{− n} för att definiera F _n , är slutvärdet 1 + 2 c istället för 5. Varje konstant större än 3 ger en korrekt påstående av lemma, men inte 3.
• Med hjälp av en finare analys, när den ursprungliga samlingen F är en Vitali-täckning av en delmängd E av Rd , visar man att delsamlingen G , definierad i ovanstående bevis, täcker E upp till en Lebesgue-försumbar mängd ^.

Tillämpningar och användningssätt

En tillämpning av Vitali-lemmat är att bevisa Hardy–Littlewoods maximala ojämlikhet . Liksom i detta bevis används Vitali-lemmat ofta när vi till exempel betraktar det d -dimensionella Lebesgue-måttet , $\lambda _{d}$ , för en mängd E ⊂ R ^d , som vi känner till ingår i föreningen av en viss samling bollar $\{B_{j}:j\in J\}$ , som var och en har ett mått som vi lättare kan beräkna, eller har en speciell egendom man skulle vilja exploatera. Därför, om vi beräknar måttet för denna förening, kommer vi att ha en övre gräns på måttet E . Det är dock svårt att beräkna måttet på föreningen av alla dessa bollar om de överlappar varandra. Med Vitali-lemmat kan vi välja en undersamling $\left\{B_{j}:j\in J'\right\}$ som är disjunkt och sådan att ${\textstyle \bigcup _{j\in J'}5B_{j}\supset \bigcup _{j\in J}B_{j}\supset E}$ . Därför,

$\lambda _{d}(E)\leq \lambda _{d}{\biggl (}\bigcup _{j\in J}B_{j}{\biggr )}\leq \lambda _{d }{\biggl (}\bigcup _{j\in J'}5B_{j}{\biggr )}\leq \sum _{j\in J'}\lambda _{d}(5B_{j}).$

d -dimensionell bolls radie med en faktor fem ökar dess volym med en faktor 5 ^d , vet vi att

$\sum _{j\in J'}\lambda _{d}(5B_{j} )=5^{d}\summa _{j\in J'}\lambda _{d}(B_{j})$

och sålunda

$\lambda _{d}(E)\leq 5^{d}\sum _{j\in J'}\lambda _{d}(B_{j}).$

Vitali täckande teorem

I täckningssatsen är syftet att täcka, upp till en "försumbar mängd", en given mängd E ⊆ R ^d av en disjunkt delsamling extraherad från en Vitali-beläggning för E : en Vitali-klass eller Vitali-beläggning ${\ mathcal {V}}$ för E är en samling mängder så att det för varje x ∈ E och δ > 0 finns en mängd U i samlingen ${\mathcal {V}}$ så att x ∈ U och diametern på U är icke-noll och mindre än δ .

I den klassiska miljön av Vitali är den försumbara mängden en Lebesgue försumbar mängd ^, men andra mått än Lebesgue-måttet och andra utrymmen än Rd har också beaktats, vilket visas i det relevanta avsnittet nedan.

Följande observation är användbar: om ${\mathcal {V}}$ är en Vitali-täckning för E och om E ingår i en öppen mängd Ω ⊆ R ^d , då undersamlingen av mängder U i ${\mathcal {V}}$ som ingår i Ω är också en Vitali-beläggning för E .

Vitalis täckande teorem för Lebesgue-måttet

Nästa täckande teorem för Lebesguemåttet λ _d beror på Lebesgue (1910) . En samling ${\mathcal {V}}$ av mätbara delmängder av R ^d är en vanlig familj (i betydelsen Lebesgue ) om det finns en konstant C så att

$\operatorname {diam} (V)^{d}\leq C\,\lambda _{d}(V)$

för varje uppsättning V i samlingen ${\mathcal {V}}$ . Kuberfamiljen är ett exempel på vanlig familj ${\mathcal {V}}$ , liksom familjen ${\mathcal {V}}(m)$ av rektanglar i R ² så att förhållandet mellan sidorna förblir mellan m ⁻¹ och m , för vissa fasta m ≥ 1. Om en godtycklig norm ges på R ^d , är familjen av kulor för metriken som är associerad med normen ett annat exempel. Tvärtom är familjen av alla rektanglar i R ² inte regelbunden.

Sats — Låt E ⊆ R ^d vara en mätbar mängd med ändligt Lebesgue-mått, och låt ${\mathcal {V}}$ vara en vanlig familj av slutna delmängder av R ^d som är en Vitali-täckning för E . Då finns det en ändlig eller räkningsbart oändlig disjunkt undersamling $\{U_{j}\}\subseteq {\mathcal {V}}$ så att

$$\lambda _{d}{\biggl (}E\setminus \bigcup _{j}U_{j}{\biggr )}=0.$$

Det ursprungliga resultatet av Vitali (1908) är ett specialfall av denna sats, där d = 1 och ${\mathcal {V}}$ är en samling intervall som är en Vitali som täcker en mätbar delmängd E av den verkliga linjen har ändligt mått. Satsen ovan förblir sann utan att anta att E har ändligt mått. Detta erhålls genom att applicera täckningsresultatet i det finita måttet fall, för varje heltal n ≥ 0, på den del av E som finns i den öppna ringen Ω _n av punkterna x så att n < | x | < n +1.

En något besläktad täckningssats är Besicovitchs täckande teorem . Till varje punkt a i en delmängd A ⊆ R ^{d ,} tilldelas en euklidisk boll B ( a , r _a ) med centrum a och positiv radie r _{a .} Sedan, som i Vitali-satsen, väljs en undersamling av dessa bollar för att täcka A på ett specifikt sätt. Huvudskillnaderna med Vitali-täckningssatsen är att å ena sidan är osamningskravet för Vitali lättat till det faktum att antalet N _x av de valda kulorna som innehåller en godtycklig punkt x ∈ R ^d begränsas av en konstant B _d som endast beror på på dimensionen d ; å andra sidan täcker de valda bollarna uppsättningen A för alla givna centra.

Vitalis täckande teorem för Hausdorff-måttet

Man kan ha ett liknande mål när man överväger Hausdorff-mått istället för Lebesgue-mått. Följande sats gäller i så fall.

Teorem — Låt H ^s beteckna s -dimensionellt Hausdorff-mått, låt E ⊆ R ^d vara en H ^s - mätbar mängd och ${\mathcal {V}}$ en Vitali-klass av slutna mängder för E . Då finns det en (ändlig eller räkningsbart oändlig) disjunkt undersamling $\{U_{j}\}\subseteq {\mathcal {V}}$ så att antingen

$$H^{s}\left(E\setminus \bigcup _{j}U_{j}\right)=0$$

eller

$$\sum _{j}\operatörsnamn {diam} (U_{j})^{s}=\infty .$$

Dessutom, om E har ändligt s -dimensionellt Hausdorff-mått, kan vi för valfri ε > 0 välja denna undersamling { U _j } så att

$H^{s}(E)\leq \sum _{j}\mathrm {diam} (U_{j})^{s}+\varepsilon .$

Detta teorem antyder resultatet av Lebesgue som ges ovan. I själva verket, när s = d ^{, sammanfaller} Hausdorff-måttet Hs på Rd med en multipel av det d -dimensionella Lebesgue-måttet ^. Om en disjunkt samling $\{U_{j}\}$ är regelbunden och ingår i ett mätbart område B med ändligt Lebesgue-mått, då

$\sum _{j}\operatörsnamn {diam} (U_{j})^ {d}\leq C\sum _{j}\lambda _{d}(U_{j})\leq C\,\lambda _{d}(B)<+\infty$

vilket utesluter den andra möjligheten i det första påståendet i föregående sats. Det följer att E omfattas, upp till en Lebesgue-försumbar uppsättning, av den valda disjunkta undersamlingen.

Från täcklemmat till täckande sats

Det täckande lemmat kan användas som ett mellansteg i bevisningen av följande grundläggande form av Vitali-täckningssatsen.

Teorem — För varje delmängd E av R ^d och varje Vitali-täcke av E av en samling F av slutna bollar, finns det en disjunkt delsamling G som täcker E upp till en Lebesgue-försumbar mängd.

Bevis: Utan förlust av generalitet kan man anta att alla kulor i F är icke degenererade och har en radie mindre än eller lika med 1. Genom den oändliga formen av det täckande lemma finns det en räknebar disjunkt undersamling $\mathbf {G }$ av F så att varje boll B ∈ F skär en boll C ∈ G för vilken B ⊂ 5 C . Låt r > 0 ges, och låt Z beteckna uppsättningen av punkter z ∈ E som inte finns i någon boll från G och som tillhör den öppna bollen B ( r ) med radien r , centrerad på 0. Det räcker med att visa att Z är Lebesgue-försumbar, för varje given r .

Låt $\mathbf {G} _{r}=\{C_{n}\}_{n}$ beteckna undersamlingen av de kulor i G som möter B ( r ). Observera att $\mathbf {G} _{r}$ kan vara ändlig eller oändlig. Låt z ∈ Z vara fixerad. För varje N tillhör z inte den slutna mängden $K=\bigcup _{n\leq N}C_{n}$ enligt definitionen av Z . Men genom Vitali-täckningsegenskapen kan man hitta en boll B ∈ F som innehåller z , som finns i B ( r ), och disjunkt från K . Genom egenskapen G skär bollen B någon boll $C_{i}\in \mathbf {G}$ och ingår i $5C_{i}$ . Men eftersom K och B är disjunkta måste vi ha i > N. Så $z\in 5C_{i}$ för vissa i > N, och därför

$Z\subset \bigcup _{n>N}5C_{n}.$

Detta ger för varje N ojämlikheten

$\lambda _{d}(Z)\leq \sum _{n>N}\lambda _{d}(5C_{n})=5^{d}\summa _{n>N}\lambda _{d}(C_{n}).$

Men eftersom bollarna i $\mathbf {G} _{r}$ finns i B(r+2) , och dessa bollar är osammanhängande ser vi

$\sum _{n}\lambda _{d}(C_{n})<\infty .$

Därför konvergerar termen på höger sida av ovanstående olikhet till 0 när N går till oändligheten, vilket visar att Z är försumbar vid behov.

Oändliga dimensionella utrymmen

Vitali-täckningssatsen är inte giltig i oändliga dimensioner. Det första resultatet i denna riktning gavs av David Preiss 1979: det finns ett Gaussiskt mått γ på ett (oändligt dimensionellt) separerbart Hilbert-rum H så att Vitali-täckningssatsen misslyckas för ( H , Borel( H ), γ ). Detta resultat stärktes 2003 av Jaroslav Tišer: Vitali-täckningssatsen misslyckas faktiskt för varje oändligt dimensionellt Gaussiskt mått på något (oändligt dimensionellt) separerbart Hilbert-rum.

Se även

• Besicovitch täckande teorem

Anteckningar

•     Evans, Lawrence C.; Gariepy, Ronald F. (1992), Measure Theory and Fine Properties of Functions , Studies in Advanced Mathematics, Boca Raton, FL : CRC Press , s. viii+268, ISBN 0-8493-7157-0 , MR 1158660 , Zbl 8081 .4bl 8081
•     Falconer, Kenneth J. (1986), Fraktaluppsättningarnas geometri , Cambridge Tracts in Mathematics, vol. 85, Cambridge: Cambridge University Press , s. xiv+162, ISBN 0-521-25694-1 , MR 0867284 , Zbl 0587.28004
• "Vitali theorem" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
•   Lebesgue, Henri (1910), "Sur l'intégration des fonctions discontinues" , Annales Scientifiques de l'École Normale Supérieure , 27 : 361–450, doi : 10.24033/asens.624 , JFM 7.01045 41 .
•    Natanson, I. P (1955), Theory of functions of a real variabel , New York: Frederick Ungar Publishing Co., sid. 277, MR 0067952 , Zbl 0064.29102
•     Preiss, David (1979), "Gaussiska mått och täckteorem", Commentatione Mathematicae Universitatis Carolinae , 20 (1): 95–99, ISSN 0010-2628 , MR 0526149 , Zbl 0386.28015
•     Stein, Elias M. ; Shakarchi, Rami (2005), Verklig analys. Measure theory, integration, and Hilbert spaces , Princeton Lectures in Analysis, III, Princeton, NJ : Princeton University Press, s. xx+402, ISBN 0-691-11386-6 , MR 2129625 , Zbl 1081.28001
•    Tišer, Jaroslav (2003), "Vitali covering theorem in Hilbert space", Transactions of the American Mathematical Society , 355 (8): 3277–3289 (elektronisk), doi : 10.1090 /S0002-9947-03-03296-3 , 1974687 , Zbl 1042.28014
•   Vitali, Giuseppe (1908) [17 december 1907], "Sui gruppi di punti e sulle funzioni di variabili reali" , Atti dell'Accademia delle Scienze di Torino (på italienska), 43 : 75–92, JFM 39.0101.05 (Titel translation) " Om grupper av punkter och funktioner av reella variabler " är uppsatsen som innehåller det första beviset för Vitalis täckande sats .