Vektor sfäriska övertoner

Inom matematiken är vektorsfäriska övertoner ( VSH ) en förlängning av de skalära sfäriska övertonerna för användning med vektorfält . Komponenterna i VSH är komplext värderade funktioner uttryckta i de sfäriska koordinatbasvektorerna .

Definition

Flera konventioner har använts för att definiera VSH. Vi följer det av Barrera et al. . Givet en skalär sfärisk överton Y _ℓm ( θ , φ ) , definierar vi tre VSH:

• $\mathbf {Y} _{\ell m}=Y_{\ell m}{\hat {\mathbf {r} }},$
• $\mathbf {\Psi } _{\ell m}=r\nabla Y_{\ell m},$
• $\mathbf {\Phi } _{\ell m}=\mathbf {r} \times \nabla Y_{\ell m},$

där ${\hat {\mathbf {r} }}$ är enhetsvektorn längs den radiella riktningen i sfäriska koordinater och $\mathbf {r}$ vektorn längs den radiella riktningen med samma norm som radien, dvs $\mathbf {r} =r{\hat {\mathbf {r} }}$ . De radiella faktorerna är inkluderade för att garantera att dimensionerna för VSH är desamma som de för de vanliga sfäriska övertonerna och att VSH inte beror på den radiella sfäriska koordinaten.

Intresset med dessa nya vektorfält är att separera det radiella beroendet från det vinkelmässiga när man använder sfäriska koordinater, så att ett vektorfält tillåter en multipolexpansion

$$\mathbf {E} =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell}\left(E_{\ell m}^{r }(r)\mathbf {Y} _{\ell m}+E_{\ell m}^{(1)}(r)\mathbf {\Psi } _{\ell m}+E_{\ell m} ^{(2)}(r)\mathbf {\Phi } _{\ell m}\right).$$

Etiketterna på komponenterna reflekterar att $E_{\ell m}^{r}$ är den radiella komponenten i vektorfältet, medan $E_{\ell m} ^{(1)}$ och $E_{\ell m}^{(2)}$ är tvärgående komponenter (med avseende på radievektorn $\mathbf {r}$ ).

Huvudegenskaper

Symmetri

Liksom de skalära sfäriska övertonerna uppfyller VSH

$$_ displaystyle {\begin{aligned}\mathbf {Y} _{\ell ,-m}&=(-1)^{m}\mathbf {Y} _{\ell m}^{*},\\\mathbf {\Psi } _{\ell ,-m}&=(-1)^{m}\mathbf {\Psi } _{\ell m}^{*},\\\mathbf {\Phi} _{\ ell ,-m}&=(-1)^{m}\mathbf {\Phi } _{\ell m}^{*},\end{aligned}}}$$

vilket halverar antalet oberoende funktioner ungefär. Stjärnan indikerar komplex konjugation .

Ortogonalitet

VSH är ortogonala på det vanliga tredimensionella sättet vid varje punkt $\mathbf {r}$ :

$${\begin{aligned}\mathbf {Y} _{\ell m}(\mathbf {r} )\cdot \mathbf {\Psi } _{\ell m}(\mathbf {r} )&=0,\\\mathbf {Y} _{\ell m}(\mathbf {r} )\cdot \mathbf {\Phi } _{\ell m}(\mathbf {r} )&=0,\\\mathbf {\Psi } _{\ell m}(\mathbf {r} )\cdot \mathbf {\Phi } _{\ell m}(\mathbf {r} )&=0.\end{aligned}}$$

De är också ortogonala i Hilbert-rymden:

$${\begin{aligned}\int \mathbfell\Y} cdot \mathbf {Y} _{\ell 'm'}^{*}\,d\Omega &=\delta _{\ell \ell '}\delta _{mm'},\\\int \mathbf { \Psi } _{\ell m}\cdot \mathbf {\Psi } _{\ell 'm'}^{*}\,d\Omega &=\ell (\ell +1)\delta _{\ell \ell '}\delta _{mm'},\\\int \mathbf {\Phi} _{\ell m}\cdot \mathbf {\Phi} _{\ell 'm'}^{*}\, d\Omega &=\ell (\ell +1)\delta _{\ell \ell '}\delta _{mm'},\\\int \mathbf {Y} _{\ell m}\cdot \mathbf {\Psi } _{\ell 'm'}^{*}\,d\Omega &=0,\\\int \mathbf {Y} _{\ell m}\cdot \mathbf {\Phi} _{ \ell 'm'}^{*}\,d\Omega &=0,\\\int \mathbf {\Psi } _{\ell m}\cdot \mathbf {\Phi } _{\ell 'm' }^{*}\,d\Omega &=0.\end{aligned}}$$

Ett ytterligare resultat vid en enda punkt $\mathbf {r}$ (inte rapporterat i Barrera et al, 1985) är för alla $\ell ,m,\ell ',m'$ ,

$${\begin{aligned}\} _mathbf {\displaystyle {\begin{aligned}\} {\ell m}(\mathbf {r} )\cdot \mathbf {\Psi } _{\ell 'm'}(\mathbf {r} )&=0,\\\mathbf {Y} _{\ell m}(\mathbf {r} )\cdot \mathbf {\Phi } _{\ell 'm'}(\mathbf {r} )&=0.\end{aligned}}$$

Vector flerpoliga ögonblick

Ortogonalitetsrelationerna tillåter en att beräkna de sfäriska multipolmomenten för ett vektorfält som

$${\begin{aligned}E_{\ell m}^{r}&=\int \mathbf {E} \cdot \mathbf {Y} _{\ell m}^{*}\,d\Omega ,\\E_{\ell m}^{(1)}&={\frac {1}{\ell (\ell +1)}}\int \mathbf {E} \cdot \mathbf {\Psi } _ {\ell m}^{*}\,d\Omega ,\\E_{\ell m}^{(2)}&={\frac {1}{\ell (\ell +1)}}\int \mathbf {E} \cdot \mathbf {\Phi } _{\ell m}^{*}\,d\Omega .\end{aligned}}$$

Gradienten för ett skalärt fält

Med tanke på multipolexpansionen av ett skalärt fält

$$\phi =\sum _{\ell =0}^{\infty }\summa _ {m=-\ell }^{\ell }\phi _{\ell m}(r)Y_{\ell m}(\theta ,\phi ),$$

vi kan uttrycka dess gradient i termer av VSH som

$$\nabla \phi =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left({\frac {d\phi _{\ ell m}}{dr}}\mathbf {Y} _{\ell m}+{\frac {\phi _{\ell m}}{r}}\mathbf {\Psi } _{\ell m}\ höger).$$

Divergens

För alla multipolfält vi har

$${\begin{aligned}\nabla \cdot \left(f(r)\mathbf {Y} _{\ell m}\right)& =\left({\frac {df}{dr}}+{\frac {2}{r}}f\right)Y_{\ell m},\\\nabla \cdot \left(f(r)\ mathbf {\Psi } _{\ell m}\right)&=-{\frac {\ell (\ell +1)}{r}}fY_{\ell m},\\\nabla \cdot \left( f(r)\mathbf {\Phi } _{\ell m}\right)&=0.\end{aligned}}$$

Genom superposition får vi divergensen för vilket vektorfält som helst:

$$\nabla \cdot \mathbf {E} =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left({\frac {dE_ {\ell m}^{r}}{dr}}+{\frac {2}{r}}E_{\ell m}^{r}-{\frac {\ell (\ell +1)}{ r}}E_{\ell m}^{(1)}\right)Y_{\ell m}.$$

Vi ser att komponenten på Φℓm alltid _. är solenoid

Ringla

För alla multipolfält vi har

$${\begin{aligned}\nabla \times \left(f(r)\mathbf {Y} _{\ell m}\right)&=-{\frac {1}{r}}f\mathbf {\Phi } _{\ell m},\\\nabla \times \left(f(r)\mathbf {\Psi } _{\ell m}\right)&=\left({\frac {df} {dr}}+{\frac {1}{r}}f\right)\mathbf {\Phi} _{\ell m},\\\nabla \times \left(f(r)\mathbf {\Phi } _{\ell m}\right)&=-{\frac {\ell (\ell +1)}{r}}f\mathbf {Y} _{\ell m}-\left({\frac { df}{dr}}+{\frac {1}{r}}f\right)\mathbf {\Psi } _{\ell m}.\end{aligned}}$$

Genom superposition får vi krullen för vilket vektorfält som helst:

$$\nabla \times \mathbf {E} =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell}\left(-{\frac { \ell (\ell +1)}{r}}E_{\ell m}^{(2)}\mathbf {Y} _{\ell m}-\left({\frac {dE_{\ell m} ^{(2)}}{dr}}+{\frac {1}{r}}E_{\ell m}^{(2)}\right)\mathbf {\Psi } _{\ell m}+ \left(-{\frac {1}{r}}E_{\ell m}^{r}+{\frac {dE_{\ell m}^{(1)}}{dr}}+{\frac {1}{r}}E_{\ell m}^{(1)}\right)\mathbf {\Phi } _{\ell m}\right).$$

Laplacian

Laplace-operatorns åtgärd $\Delta =\nabla \cdot \nabla$ separeras enligt följande:

$$\Delta \left(f(r) \mathbf {Z} _{\ell m}\right)=\left({\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}r^{2} {\frac {\partial f}{\partial r}}\right)\mathbf {Z} _{\ell m}+f(r)\Delta \mathbf {Z} _{\ell m},$$

där $\mathbf {Z} _{\ell m}=\mathbf {Y} _{\ell m},\mathbf {\Psi } _ {\ell m},\mathbf {\Phi } _{\ell m}$ och

$${\begin{aligned}\Delta \mathbf {Y} _{\ell m}&=-{\frac {1}{r^{2}}}(2+\ell (\ell +1) )\mathbf {Y} _{\ell m}+{\frac {2}{r^{2}}}\mathbf {\Psi } _{\ell m},\\\Delta \mathbf {\Psi } _{\ell m}&={\frac {2}{r^{2}}}\ell (\ell +1)\mathbf {Y} _{\ell m}-{\frac {1}{r ^{2}}}\ell (\ell +1)\mathbf {\Psi } _{\ell m},\\\Delta \mathbf {\Phi } _{\ell m}&=-{\frac { 1}{r^{2}}}\ell (\ell +1)\mathbf {\Phi } _{\ell m}.\end{aligned}}$$

Observera också att denna åtgärd blir symmetrisk , dvs. de off-diagonala koefficienterna är lika med ${\textstyle {\frac {2}{r^{2}}}{\sqrt {\ell ( \ell +1)}}}$ , för korrekt normaliserad VSH.

Exempel

$\mathbf {\Psi } _{1m}$

$\mathbf {\Psi } _{2m}$

$\mathbf {\Psi } _{3m}$

$\mathbf {\Phi } _{1m}$

$\mathbf {\Phi } _{2m}$

$\mathbf {\Phi } _{3m}$

Visualiseringar av de verkliga delarna av $\ell =1,2,3$ VSH. Klicka för att expandera.

Första vektorsfäriska övertoner

• $\ell =0$ .
  $${\begin{aligned}\mathbf {Y} _{00}&={\sqrt {\frac {1}{4\pi }}}{\hat {\mathbf {r} }},\\ \mathbf {\Psi } _{00}&=\mathbf {0} ,\\\mathbf {\Phi } _{00}&=\mathbf {0} .\end{aligned}}$$
• $\ell =1$ .
  $${\begin{aligned}\mathbf {Y} _{10}&={\ sqrt {\frac {3}{4\pi }}}\cos \theta \,{\hat {\mathbf {r} }},\\\mathbf {Y} _{11}&=-{\sqrt { \frac {3}{8\pi }}}e^{i\varphi }\sin \theta \,{\hat {\mathbf {r} }},\end{aligned}}$$
  $${\begin{aligned}\mathbf {\Psi }} _{10}&=-{\sqrt {\frac {3}{4\pi }}}\sin \theta \,{\hat {\mathbf {\theta} }},\\\mathbf {\Psi } _{11}&=-{\sqrt {\frac {3}{8\pi }}}e^{i\varphi }\left(\cos \theta \,{\hat {\mathbf {\theta} } }+i\,{\hat {\mathbf {\varphi } }}\right),\end{aligned}}$$
  $${\begin{aligned}\mathbf {\Phi } _{10}&=-{\sqrt {\frac {3}{4\pi }}}\sin \theta \,{\hat {\mathbf {\varphi } }},\\\mathbf {\Phi} _{11}&={\sqrt {\frac {3}{8\pi }}}e^{i\varphi }\left(i\, {\hat {\mathbf {\theta } }}-\cos \theta \,{\hat {\mathbf {\varphi } }}\right).\end{aligned}}$$
• $\ell =2$ .
  $${\begin{aligned}\mathbf {Y} _{20}&={\frac {1}{4}}{\sqrt {\frac {5}{\pi }}}\,(3\ cos ^{2}\theta -1)\,{\hat {\mathbf {r}}},\\\mathbf {Y} _{21}&=-{\sqrt {\frac {15}{8\ pi }}}\,\sin \theta \,\cos \theta \,e^{i\varphi }\,{\hat {\mathbf {r} }},\\\mathbf {Y} _{22} &={\frac {1}{4}}{\sqrt {\frac {15}{2\pi }}}\,\sin ^{2}\theta \,e^{2i\varphi }\,{ \hat {\mathbf {r} }}.\end{aligned}}$$
  $${\begin{aligned}\mathbf {\Psi } _{20}&=-{\frac {3}{2}}{\sqrt {\frac {5}{\pi }}}\,\ sin \theta \,\cos \theta \,{\hat {\mathbf {\theta} }},\\\mathbf {\Psi } _{21}&=-{\sqrt {\frac {15}{8 \pi }}}\,e^{i\varphi }\,\left(\cos 2\theta \,{\hat {\mathbf {\theta} }}+i\cos \theta \,{\hat { \mathbf {\varphi } }}\right),\\\mathbf {\Psi } _{22}&={\sqrt {\frac {15}{8\pi }}}\,\sin \theta \, e^{2i\varphi }\,\left(\cos \theta \,{\hat {\mathbf {\theta} }}+i\,{\hat {\mathbf {\varphi} }}\right). \end{aligned}}$$
  $${\begin{aligned}\mathbf {\Phi } _{20}&=-{\frac {3}{2}}{\sqrt {\frac {5}{\pi }}}\sin \ theta \,\cos \theta \,{\hat {\mathbf {\varphi} }},\\\mathbf {\Phi} _{21}&={\sqrt {\frac {15}{8\pi } }}\,e^{i\varphi }\,\left(i\cos \theta \,{\hat {\mathbf {\theta} }}-\cos 2\theta \,{\hat {\mathbf { \varphi } }}\right),\\\mathbf {\Phi} _{22}&={\sqrt {\frac {15}{8\pi }}}\,\sin \theta \,e^{ 2i\varphi }\,\left(-i\,{\hat {\mathbf {\theta} }}+\cos \theta \,{\hat {\mathbf {\varphi} }}\right).\end {Justerat}}$$

Uttryck för negativa värden på m erhålls genom att tillämpa symmetrirelationerna.

Ansökningar

Elektrodynamik

VSH är särskilt användbar vid studiet av flerpoliga strålningsfält . Till exempel beror en magnetisk multipol på en oscillerande ström med vinkelfrekvens $\omega$ och komplex amplitud

$${\hat {\mathbf {J} }}=J(r)\mathbf {\Phi } _{\ell m},$$

och motsvarande elektriska och magnetiska fält, kan skrivas som

$${\begin{aligned}{\hat {\mathbf {E} }}&=E(r)\mathbf {\Phi} _{\ell m},\\{\hat {\mathbf {B} }}&=B^{r}(r)\mathbf {Y} _{\ell m}+B^{(1)}(r)\mathbf {\Psi } _{\ell m}.\end{ Justerat}}$$

Genom att ersätta Maxwells ekvationer, är Gauss lag automatiskt uppfylld

$$\nabla \cdot {\hat {\mathbf {E} }}=0,$$

medan Faradays lag frikopplar som

$$\nabla \times {\hat {\mathbf {E} }}=-i\omega {\hat {\mathbf {B} }}\quad \Rightarrow \quad {\begin{cases}{\dfrac { \ell (\ell +1)}{r}}E=i\omega B^{r},\\{\dfrac {dE}{dr}}+{\dfrac {E}{r}}=i\ omega B^{(1)}.\end{cases}}$$

Gauss lag för magnetfältet innebär

$$\nabla \cdot {\hat {\mathbf {B} }}=0 \quad \Rightarrow \quad {\frac {dB^{r}}{dr}}+{\frac {2}{r}}B^{r}-{\frac {\ell (\ell +1)} {r}}B^{(1)}=0,$$

och Ampère–Maxwells ekvation ger

$$\nabla \times {\hat {\mathbf {B} }}=\mu _{0}{\hat {\mathbf {J} }}+i\mu _{0}\varepsilon _{0} \omega {\hat {\mathbf {E} }}\quad \Rightarrow \quad -{\frac {B^{r}}{r}}+{\frac {dB^{(1)}}{dr} }+{\frac {B^{(1)}}{r}}=\mu _{0}J+i\omega \mu _{0}\varepsilon _{0}E.$$

På detta sätt har de partiella differentialekvationerna omvandlats till en uppsättning vanliga differentialekvationer.

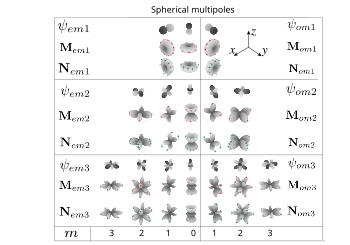
Alternativ definition

Vinkel del av magnetiska och elektriska vektorsfäriska övertoner. Röda och gröna pilar visar fältets riktning. Genererande skalära funktioner presenteras också, endast de tre första ordningarna visas (dipoler, kvadrupoler, oktupoler).

I många tillämpningar definieras vektorsfäriska övertoner som grundläggande uppsättning av lösningarna för vektor Helmholtz-ekvationen i sfäriska koordinater.

I det här fallet genereras vektorsfäriska övertoner av skalära funktioner, som är lösningar av skalär Helmholtz-ekvation med vågvektorn $\mathbf {k}$ .

$${ \begin{array}{l}{\psi _{emn}=\cos m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r)}\\{\ psi _{omn}=\sin m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r)}\end{array}}$$

här är $P_{n}^{m}(\cos \theta )$ de associerade Legendre-polynomen och $z_{n}({k }r)$ är någon av de sfäriska Bessel-funktionerna .

Vektorsfäriska övertoner definieras som:

longitudinella övertoner

$\mathbf {L} _{^{e}_{o}mn}=\mathbf {\nabla } \psi _{^{e}_ {o}mn}$

magnetiska övertoner

$\mathbf {M} _{^{e}_{o}mn}=\nabla \times \ vänster(\mathbf {r} \psi _{^{e}_{o}mn}\right)$

elektriska övertoner

$\mathbf {N} _ {^{e}_{o}mn}={\frac {\nabla \times \mathbf {M} _{^{e}_{o}mn}}{k}}$

Här använder vi övertoner med verkligt värde vinkeldel, där ${\displaystyle m\geq 0} ,$ men komplexa funktioner kan introduceras på samma sätt.

Låt oss introducera notationen $\rho =kr$ . I komponentformen skrivs vektorsfäriska övertoner som:

$${\begin{aligned}{\mathbf {M} _{emn}(k,\mathbf {r} )=\qquad {{ \frac {-m}{\sin(\theta )}}\sin(m\varphi )P_{n}^{m}(\cos(\theta ))}z_{n}(\rho )\mathbf { e} _{\theta }}\\{{}-\cos(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}}z_ {n}(\rho )\mathbf {e} _{\varphi }\end{aligned}}$$

$${\begin{aligned}{\mathbf {M} _{omn}(k,\mathbf {r} )=\qquad {{\ frac {m}{\sin(\theta )}}\cos(m\varphi )P_{n}^{m}(\cos(\theta ))}}z_{n}(\rho )\mathbf {e } _{\theta }\\{{}-\sin(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}z_{n} (\rho )\mathbf {e} _{\varphi }}\end{aligned}}$$

$${\begin{aligned}{\mathbf {N} _{emn}(k,\mathbf {r} )=\qquad {\frac {z_{ n}(\rho )}{\rho }}\cos(m\varphi )n(n+1)P_{n}^{m}(\cos(\theta ))\mathbf {e} _{\mathbf {r} }}\\{{}+\cos(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}}{\frac { 1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\theta }\\{{} -m\sin(m\varphi ){\frac {P_{n}^{m}(\cos(\theta ))}{\sin(\theta )}}}{\frac {1}{\rho } }{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\varphi }\end{aligned}}$$

$${\begin{aligned}\mathbf {N} _{omn}(k,\mathbf {r} )=\qquad {\frac {z_{n }(\rho )}{\rho }}\sin(m\varphi )n(n+1)P_{n}^{m}(\cos(\theta ))\mathbf {e} _{\mathbf { r} }\\{}+\sin(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}{\frac {1}{\ rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\theta }\\{}+{m\cos (m\varphi ){\frac {P_{n}^{m}(\cos(\theta ))}{\sin(\theta )}}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\varphi }\end{aligned}}$$

Det finns ingen radiell del för magnetiska övertoner. För elektriska övertoner minskar den radiella delen snabbare än vinkeln, och för stora $\rho$ försummas. Vi kan också se att för elektriska och magnetiska övertoner är vinkeldelar desamma fram till permutation av de polära och azimutala enhetsvektorerna, så för stora $\rho$ är elektriska och magnetiska övertonsvektorer lika i värde och vinkelräta mot varandra .

Längsgående övertoner:

$${\begin{aligned}\mathbf {L} _{^{e}_{o}{mn}}(k,\mathbf {r}){}=\qquad &{\frac {\partial }{\partial r}}z_{n}(kr)P_ {n}^{m}(\cos \theta ){^{\cos }_{\sin }}{m\varphi }\mathbf {e} _{r}\\{}+{}&{\frac {1}{r}}z_{n}(kr){\frac {\partial }{\partial \theta }}P_{n}^{m}(\cos \theta ){^{\cos }_{ \sin }}m\varphi \mathbf {e} _{\theta }\\{}\mp {}&{\frac {m}{r\sin \theta }}z_{n}(kr)P_{n }^{m}(\cos \theta ){^{\sin }_{\cos }}m\varphi \mathbf {e} _{\varphi }\end{aligned}}$$

Ortogonalitet

Lösningarna av Helmholtz vektorekvation följer följande ortogonalitetsrelationer:

$${\begin{aligned}\int _{0}^{2 \pi }\int _{0}^{\pi }\mathbf {L} _{^{e}_{o}mn}\cdot \mathbf {L} _{^{e}_{o}mn} \sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{(2n+1)^{2}}}{\frac {(n +m)!}{(nm)!}}k^{2}\left\{n\left[z_{n-1}(kr)\höger]^{2}+(n+1)\left[ z_{n+1}(kr)\right]^{2}\right\}\\[3pt]\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {M} _{^{e}_{o}mn}\cdot \mathbf {M} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\ delta _{m,0}){\frac {2\pi }{2n+1}}{\frac {(n+m)!}{(nm)!}}n(n+1)\left[z_ {n}(kr)\right]^{2}\\[3pt]\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {N} _{^{ e}_{o}mn}\cdot \mathbf {N} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0} ){\frac {2\pi }{(2n+1)^{2}}}{\frac {(n+m)!}{(nm)!}}n(n+1)\left\{( n+1)\vänster[z_{n-1}(kr)\höger]^{2}+n\vänster[z_{n+1}(kr)\höger]^{2}\höger\}\\ [3pt]\int _{0}^{\pi }\int _{0}^{2\pi }\mathbf {L} _{^{e}_{o}mn}\cdot \mathbf {N} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{(2n+1) ^{2}}}{\frac {(n+m)!}{(nm)!}}n(n+1)k\left\{\left[z_{n-1}(kr)\right] ^{2}-\left[z_{n+1}(kr)\right]^{2}\right\}\end{aligned}}$$

Alla andra integraler över vinklarna mellan olika funktioner eller funktioner med olika index är lika med noll.

Rotation och inversion

Illustration av transformationen av vektorsfäriska övertoner under rotationer. Man kan se att de transformeras på samma sätt som motsvarande skalära funktioner.

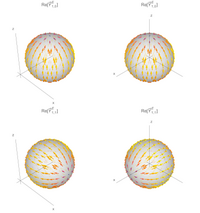
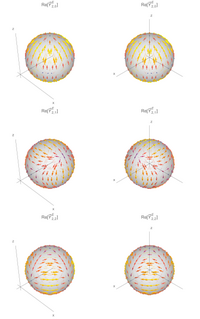
Under rotation transformeras vektorsfäriska övertoner genom varandra på samma sätt som motsvarande skalära sfäriska funktioner , som genererar för en specifik typ av vektorövertoner. Till exempel, om genereringsfunktionerna är de vanliga sfäriska övertonerna , kommer vektorövertonerna också att transformeras genom Wigner D-matriserna

$${\hat {D}}(\alpha ,\beta ,\gamma )\mathbf {Y} _{JM}^{(s)}(\theta ,\varphi ) =\sum _{m'=-\ell }^{\ell [D_{MM'}^{(\ell )}(\alpha ,\beta ,\gamma )]^{*}\mathbf {Y} _{JM'}^{(s)}(\theta ,\varphi ),$$

Beteendet under rotationer är detsamma för elektriska, magnetiska och longitudinella övertoner.

Under inversion uppträder elektriska och longitudinella sfäriska övertoner på samma sätt som skalära sfäriska funktioner, dvs.

$${\hat {I}}\mathbf {N} _{JM}(\theta ,\varphi )=(-1)^{J}\mathbf {N} _{JM}(\theta ,\varphi ),$$

och magnetiska har motsatt paritet:

$${\hat {I}}\mathbf {M} _{JM}(\theta , \varphi )=(-1)^{J+1}\mathbf {M} _{JM}(\theta ,\varphi ),$$

Vätskedynamik

Vid beräkningen av Stokes lag för det motstånd som en trögflytande vätska utövar på en liten sfärisk partikel, följer hastighetsfördelningen Navier–Stokes ekvationer och försummar tröghet, dvs.

$${\begin{aligned}0&=\nabla \cdot \mathbf {v} ,\\\mathbf {0} &=-\nabla p+\ eta \nabla ^{2}\mathbf {v} ,\end{aligned}}$$

med randvillkoren

$$\mathbf {v} ={\begin{cases}\mathbf {0} &r=a,\\-\mathbf {U} _{0}&r\to \infty .\end{cases}}$$

där U är partikelns relativa hastighet till vätskan långt från partikeln. I sfäriska koordinater kan denna hastighet i oändligheten skrivas som

$$\mathbf {U} _{0}=U_{0}\left(\cos \theta \,{\hat {\mathbf {r}}}-\sin \theta \,{\hat {\mathbf {\theta } }}\right)=U_{0}\left(\mathbf {Y} _{10}+\mathbf {\Psi } _{10}\right).$$

Det sista uttrycket antyder en expansion i sfäriska övertoner för vätskehastigheten och trycket

$${\begin{aligned}p&=p(r)Y_{10},\\\mathbf {v} &=v^{r}(r)\mathbf {Y} _{10}+v^{ (1)}(r)\mathbf {\Psi } _{10}.\end{aligned}}$$

Substitution i Navier–Stokes-ekvationerna ger en uppsättning vanliga differentialekvationer för koefficienterna.

Integrerade relationer

Här används följande definitioner:

$${\begin{aligned}Y_{emn}&=\ cos m\varphi P_{n}^{m}(\cos \theta )\\Y_{omn}&=\sin m\varphi P_{n}^{m}(\cos \theta )\end{aligned} }$$

$$\mathbf {X} _{^{e}_{o}mn}\left({\frac {\mathbf {k} }{k}}\right)=\nabla \times \left(\mathbf {k} Y_{^{o}_{e}mn}\left({\frac {\mathbf {k } }{k}}\right)\right)$$

$$\mathbf {Z} _{^{o}_{e}mn}\left({\frac { \mathbf {k} }{k}}\right)=i{\frac {\mathbf {k} }{k}}\times \mathbf {X} _{^{e}_{o}mn}\left ({\frac {\mathbf {k} }{k}}\right)$$

I fallet, när istället för $z_{n}$ är sfäriska Bessel-funktioner , kan man med hjälp av planvågsexpansion få följande integralförhållanden:

$$\mathbf {N} _{pmn}(k,\mathbf {r } )={\frac {i^{-n}}{4\pi }}\int \mathbf {Z} _{pmn}\left({\frac {\mathbf {k} }{k}}\right )e^{i\mathbf {k} \mathbf {r} }d\Omega _{k}$$

$$\mathbf {M} _{pmn}(k,\mathbf {r } )={\frac {i^{-n}}{4\pi }}\int \mathbf {X} _{pmn}\left({\frac {\mathbf {k} }{k}}\right )e^{i\mathbf {k} \mathbf {r} }d\Omega _{k}$$

Om $z_{n}$ är sfäriska Hankel-funktioner bör man använda de olika formlerna. För vektorsfäriska övertoner erhålls följande relationer:

$$\mathbf {M} _{pmn}^{(3)}(k,\mathbf {r} )={\frac {i^{-n}}{2\pi k}}\iint _ {-\infty }^{\infty }dk_{\|}{\frac {e^{i\left(k_{x}x+k_{y}y\pm k_{z}z\right)}}{ k_{z}}}\mathbf {X} _{pmn}\left({\frac {\mathbf {k} }{k}}\right)$$

$$\mathbf {N} _{pmn}^{(3)}(k,\mathbf {r} )={\frac {i^{-n}}{2\pi k}}\iint _ {-\infty }^{\infty }dk_{\|}{\frac {e^{i\left(k_{x}x+k_{y}y\pm k_{z}z\right)}}{ k_{z}}}\mathbf {Z} _{pmn}\left({\frac {\mathbf {k} }{k}}\right)$$

där ${\textstyle k_{z}={\sqrt {k^{2}-k_{x}^{2}-k_{y}^{2}} }}$ , index $(3)$ betyder att sfäriska Hankel-funktioner används.

Se även

• Sfäriska övertoner
• Spinor sfäriska övertoner
• Spinviktade sfäriska övertoner
• Elektromagnetisk strålning
• Sfärisk grund

externa länkar

• Vector sfäriska övertoner på Eric Weissteins Mathworld