Tvåstrålande jordreflektionsmodell

Tvåstrålningsmodellen för markreflektion är en flervägsradioutbredningsmodell som förutsäger vägförlusterna mellan en sändande antenn och en mottagande antenn när de är i siktlinje (LOS ) . I allmänhet har de två antennerna olika höjd. Den mottagna signalen har två komponenter, LOS-komponenten och reflektionskomponenten, som huvudsakligen bildas av en enda jordreflekterad våg.

2-Ray Ground Reflection diagram inklusive variabler för 2-ray jordreflektionsutbredningsalgoritmen.

Matematisk härledning

Från figuren kan den mottagna siktlinjekomponenten skrivas som

$r_{los}(t)=Re\left\{{ \frac {\lambda {\sqrt {G_{los}}}}{4\pi }}\ gånger {\frac {s(t)e^{-j2\pi l/\lambda }}{l}}\ höger\}$

och den jordreflekterade komponenten kan skrivas som

$r_{ gr}(t)=Åter\vänster\{{\frac {\lambda \Gamma (\theta ){\sqrt {G_{gr}}}}{4\pi }}\ gånger {\frac {s(t- \tau )e^{-j2\pi (x+x')/\lambda }}{x+x'}}\right\}$

där $s(t)$ är den sända signalen, $l$ är längden på den direkta siktlinjen (LOS), $x+x '$ är längden på den markreflekterade strålen, $G_{los}$ är den kombinerade antennförstärkningen längs LOS-vägen, $G_{gr}$ är den kombinerade antennförstärkningen längs den markreflekterade banan är $\lambda$ våglängden för transmissionen ( ${\displaystyle \lambda ={\frac {c}{f}}} ,$ där $c$ är ljusets hastighet och $f$ är sändningsfrekvensen), $\Gamma (\theta )$ är markreflektionskoefficienten och $\tau$ är fördröjningsspridningen av modell som är lika med $(x+x'-l)/c$ . Markreflektionskoefficienten är

$\Gamma (\theta )={\frac {\sin \theta -X}{\sin \theta +X}}$

där $X=X_{h}$ eller $X=X_{v}$ beroende på om signalen är horisontell respektive vertikal polariserad. $X$ beräknas enligt följande.

$X_{h}={\sqrt {\varepsilon _{g}-{\cos }^ {2}\theta }},\ X_{v}={\frac {\sqrt {\varepsilon _{g}-{\cos }^{2}\theta }}{\varepsilon _{g}}}= {\frac {X_{h}}{\varepsilon _{g}}}$

Konstanten $\varepsilon _{g}$ är den relativa permittiviteten för marken (eller generellt sett materialet där signalen reflekteras), $\theta$ är vinkeln mellan marken och den reflekterade strålen som visas i figuren ovan.

Från figurens geometri ger:

$x+x'={\sqrt {(h_{t}+h_{r})^{2}+d^{2}} }$

och

$l={\sqrt {(h_{t}-h_{r})^{2}+d^{2}}}$ ,

Därför är väglängdsskillnaden mellan dem

$\Delta d=x+x'-l={\sqrt {(h_{t}+h_{r})^{2}+d^{2}}}-{\sqrt {(h_{t}-h_{r})^{2}+d^{2} }}$

och fasskillnaden mellan vågorna är

$\Delta \phi ={\frac {2\pi \Delta d}{\lambda }}$

Effekten av den mottagna signalen är

$P_{r}=E\{|r_{los}(t)+r_{gr}(t)|^{2}\}$

där $E\{\cdot \}$ anger medelvärde (över tid).

Approximation

Om signalen är smalbandig i förhållande till den omvända fördröjningen sprids $1/\tau$ , så att $s(t)\approx s(t- \tau )$ , kan potensekvationen förenklas till

${\begin{aligned}P_{r}=E\{|s(t)|^{2}\}\left({\frac {\lambda }{4\pi }}\right)^ {2}\times \left|{\frac {{\sqrt {G_{los}}}\times e^{-j2\pi l/\lambda }}{l}}+\Gamma (\theta ){\ sqrt {G_{gr}}}{\frac {e^{-j2\pi (x+x')/\lambda }}{x+x'}}\right|^{2}&=P_{t} \left({\frac {\lambda }{4\pi }}\right)^{2}\times \left|{\frac {\sqrt {G_{los}}}{l}}+\Gamma (\ theta ){\sqrt {G_{gr}}}{\frac {e^{-j\Delta \phi }}{x+x'}}\right|^{2}\end{aligned}}$

där $P_{t}=E\{|s(t)|^{2}\}$ är den överförda effekten.

När avståndet mellan antennerna $d$ är mycket stort i förhållande till antennens höjd kan vi expandera $\Delta d=x+x'-l$ ,

${\begin{aligned}\Delta d =x+x'-l=d{\Bigg (}{\sqrt {{\frac {(h_{t}+h_{r})^{2}}{d^{2}}}+1}} -{\sqrt {{\frac {(h_{t}-h_{r})^{2}}{d^{2}}}+1}}{\Bigg )}\end{aligned}}$

använder Taylor-serien med ${\sqrt {1+x}}$ :

${\sqrt {1+x}}=1+\textstyle {\frac {1}{2}}x-{\frac { 1}{8}}x^{2}+\dots ,$

och tar bara de två första termerna,

$x+x'-l\ ungefär {\frac {d}{2}}\times \left({\frac {(h_{t}+h_{r})^{2}}{d^{2}}}-{\frac {( h_{t}-h_{r})^{2}}{d^{2}}}\right)={\frac {2h_{t}h_{r}}{d}}$

Fasskillnaden kan då approximeras som

$\Delta \phi \approx {\frac {4\pi h_{t}h_{r}}{\lambda d}}$

När $d$ är stor, $d\gg (h_{t}+h_{r})$ ,

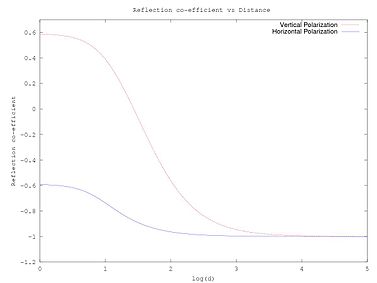
Reflektionskoefficienten tenderar till -1 för stora d.

${\begin{aligned}d&\approx l\approx x+x',\ \Gamma (\theta )\approx -1,\ G_{los}\approx G_{gr}=G\end{aligned}}$

och följaktligen

$P_{r}\approx P_{t}\left({\frac {\lambda {\sqrt {G}}}{4\pi d}}\right)^{2}\times |1- e^{-j\Delta \phi }|^{2}$

Expandera $e^{-j\Delta \phi }$ med Taylor-serien

$e^{x}=\summa _{n=0}^{\infty }{\frac {x^{n}}{n!} }=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+\cdots$

och behåller endast de två första termerna

$e^{-j\Delta \phi }\approx 1+({-j\Delta \phi })+ \cdots =1-j\Delta \phi$

det följer att

${\begin{aligned}P_{r}&\approx P_{t}\left({\frac {\lambda {\sqrt {G}}}{4\pi d}}\right)^{ 2}\times |1-(1-j\Delta \phi )|^{2}\\&=P_{t}\left({\frac {\lambda {\sqrt {G}}}{4\pi d}}\right)^{2}\times \Delta \phi ^{2}\\&=P_{t}\left({\frac {\lambda {\sqrt {G}}}{4\pi d }}\right)^{2}\times \left({\frac {4\pi h_{t}h_{r}}{\lambda d}}\right)^{2}\\&=P_{t }{\frac {Gh_{t}^{2}h_{r}^{2}}{d^{4}}}\end{aligned}}$

så att

$P_{r}\approx P_{t}{\frac {Gh_{t}^{2}h_{r}^{2}}{d ^{4}}}$

vilket är exakt i fjärrfältsområdet, dvs när $\Delta \phi \ll 1$ (vinklar mäts här i radianer, inte grader) eller, ekvivalent,

$d\gg {\frac {4\pi h_{t}h_{r}}{\lambda }}$

och där den kombinerade antennförstärkningen är produkten av sändnings- och mottagningsantennförstärkningarna, $G=G_{t}G_{r}$ . Denna formel erhölls först av BA Vvedenskij.

Observera att effekten minskar med som den omvända fjärde potensen av avståndet i fjärrfältet, vilket förklaras av den destruktiva kombinationen av de direkta och reflekterade banorna, som är ungefär av samma storlek och är 180 grader olika i fas. $G_{t}P_{t}$ kallas "effective isotropic radiated power" (EIRP), vilket är den sändningseffekt som krävs för att producera samma mottagna effekt om sändningsantennen var isotrop.

I logaritmiska enheter

I logaritmiska enheter: $P_{r_{\text{dBm}}}=P_{ t_{\text{dBm}}}+10\log _{10}(Gh_{t}^{2}h_{r}^{2})-40\log _{10}(d)$

Banförlust : $PL\;=P_{t_{\text{dBm }}}-P_{r_{\text{dBm}}}\;=40\log _{10}(d)-10\log _{10}(Gh_{t}^{2}h_{r}^ {2})$

Kraft vs. avståndsegenskaper

När avståndet $d$ mellan antenner är mindre än sändningsantennhöjden läggs två vågor till konstruktivt för att ge större effekt. När avståndet ökar, adderas dessa vågor konstruktivt och destruktivt, vilket ger områden med upp-fade och ned-fade. När avståndet ökar bortom det kritiska avståndet $dc$ eller den första Fresnel-zonen, sjunker effekten proportionellt mot en invers av fjärde potensen av $d$ . En approximation av kritiskt avstånd kan erhållas genom att sätta Δφ till π som det kritiska avståndet till ett lokalt maximum.

En förlängning till stora antennhöjder

Ovanstående uppskattningar är giltiga förutsatt att ${\displaystyle d\gg (h_{t}+h_{r})} ,$ vilket kanske inte är fallet i många scenarier, t.ex. när antennhöjderna är inte mycket mindre jämfört med avståndet, eller när marken inte kan modelleras som ett idealiskt plan. I detta fall kan man inte använda $\Gamma \approx -1$ och mer förfinad analys krävs, se t.ex.

Utbredningsmodellering för höghöjdsplattformar , UAV , drönare , etc.

Ovanstående stora antennhöjdsförlängning kan användas för att modellera en mark-till-luft-utbredningskanal som i fallet med en luftburen kommunikationsnod, t.ex. en UAV, drönare, höghöjdsplattform. När den luftburna nodens höjd är medelhög till hög, gäller inte förhållandet $d\gg (h_{t}+h_{r})$ längre, frigångsvinkeln är inte liten och följaktligen håller inte ${\displaystyle \Gamma \approx -1} heller.$ Detta har en djupgående inverkan på utbredningsvägsförlusten och typiskt fädningsdjup och den fädningsmarginal som krävs för tillförlitlig kommunikation (låg sannolikhet för avbrott).

Som ett fall av loggavståndsvägförlustmodell

Standarduttrycket för loggavståndsvägförlustmodell i [dB] är

$P_{T_{dBm}}-P_{R_{dBm} }\;=\;PL_{0}\;+\;10\nu \;\log _{10}{\frac {d}{d_{0}}}\;+\;X_{g},}$

där $X_{g}$ är storskalig (log-normal) fädning, $d_{0}$ är ett referensavstånd där vägförlusten är $PL_{0 }$ , $\nu$ är sökvägsförlustexponenten; typiskt $\nu =2...4$ . Denna modell är särskilt väl lämpad för mätningar, där $PL_{0}$ och $\nu$ bestäms experimentellt; $d_{0}$ väljs för att underlätta mätningen och för att ha en tydlig siktlinje. Denna modell är också en ledande kandidat för 5G- och 6G-system och används även för inomhuskommunikation, se t.ex. och referenser däri.

Vägförlusten [dB] för 2-strålmodellen är formellt ett specialfall med $\nu =4$ :

$;=P_{t_{dBm}} -P_{r_{dBm}}\;=40\log _{10}(d)-10\log _{10}(Gh_{t}^{2}h_{r}^{2})}$

där $d_{0}=1$ , $X_{g}=0$ , och

${\displaystyle PL_{0}=-10\log _{10}(Gh_{t}^{2}h_{r}^$ ,

vilket är giltigt det bortre fältet, $d>d_{c}=4\pi h_{r}h_{t}/\lambda$ = det kritiska avståndet.

Som ett fall av multi-slope modell

Den 2-strålade jordreflekterade modellen kan tänkas som ett fall av multi-slope-modell med brytpunkt på kritiskt avstånd med lutning 20 dB/dekad före kritiskt avstånd och lutning på 40 dB/dekad efter det kritiska avståndet. Med användning av fritt utrymme och tvåstrålningsmodellen ovan kan utbredningsvägsförlusten uttryckas som

$L=\max\{G,L_{min},L_{FS},L_{2-ray}\ }$

där $L_{FS}=(4\pi d/\lambda )^{2}$ och $L_{2-ray}=d^{4}/(h_{t}h_{r})^{2}$ är förlusterna av ledigt utrymme och 2-strålar; $L_{min}$ är en minimal vägförlust (på minsta avstånd), vanligtvis i praktiken; $L_{min}\approx 20$ dB eller så. Observera att $L\geq G$ och även $L\geq 1$ följer av lagen om energihushållning (eftersom Rx-effekten inte kan överstiga Tx-effekten) så att både $L_{FS}=(4\pi d/\lambda )^{2}$ och ${ \displaystyle L_{2-ray}=d^{4}/(h_{t}h_{r})^{2}}$ bryts ner när $d$ är tillräckligt liten. Detta bör man tänka på när man använder dessa approximationer på små avstånd (om man ignorerar denna begränsning ger ibland absurda resultat).

Se även

• Radioutbredningsmodell
• Förlust av fritt utrymme
• Friis transmissionsekvation
• ITU-R P.525
• Länkbudget
• Strålspårning (fysik)
• Reflektion (fysik)
• Speglande reflektion
• Sexstrålar modell
• Tio-strålar modell

Vidare läsning

• S. Salous, Radio Propagation Measurement and Channel Modelling, Wiley, 2013.
• JS Seybold, Introduktion till RF-utbredning, Wiley, 2005.
• K. Siwiak, Radiowave Propagation and Antennas for Personal Communications, Artech House, 1998.
• MP Doluhanov, Radiowave Propagation, Moskva: Sviaz, 1972.
• VV Nikolskij, TI Nikolskaja, Electrodynamics and Radiowave Propagation, Moskva: Nauka, 1989.
• 3GPP TR 38.901, Studie om kanalmodell för frekvenser från 0,5 till 100 GHz (Release 16), Sophia Antipolis, Frankrike, 2019 [ 2]
• Rekommendation ITU-R P.1238-8: Utbredningsdata och prediktionsmetoder för planering av inomhusradiokommunikationssystem och lokala radionät i frekvensområdet 300 MHz till 100 GHz [3 ]
• S. Loyka, ELG4179: Wireless Communication Fundamentals, Lecture Notes (Lec. 2-4), University of Ottawa, Kanada, 2021 [ 4]