True-range multilateration

True-range multilateration (även kallad avståndsintervall multilateration och sfärisk multilateration ) är en metod för att bestämma platsen för ett rörligt fordon eller stationär punkt i rymden med hjälp av flera avstånd ( avstånd ) mellan fordonet/punkten och flera rumsligt åtskilda kända platser ( ofta kallade "stationer"). Energivågor kan vara inblandade i att bestämma räckvidd, men är inte nödvändiga.

True-range multilateration är både ett matematiskt ämne och en tillämpad teknik som används inom flera områden. En praktisk tillämpning med en fast plats förekommer vid mätning . Tillämpningar som involverar fordonslokalisering kallas för navigering när personer/utrustning ombord informeras om dess plats, och benämns övervakning när enheter utanför fordonet informeras om fordonets plats.

Två lutningsområden från två kända platser kan användas för att lokalisera en tredje punkt i ett tvådimensionellt kartesiskt utrymme (plan), vilket är en ofta tillämpad teknik (t.ex. vid mätning). På liknande sätt kan två sfäriska intervall användas för att lokalisera en punkt på en sfär, vilket är ett grundläggande koncept för den antika disciplinen av himmelsnavigering - kallad höjdskärningsproblemet . Dessutom, om fler än det minsta antalet intervall är tillgängliga, är det bra att använda dem också. Den här artikeln tar upp den allmänna frågan om positionsbestämning med hjälp av flera intervall.

Inom tvådimensionell geometri är det känt att om en punkt ligger på två cirklar, så ger cirkelcentrum och de två radierna tillräcklig information för att begränsa de möjliga platserna till två - varav den ena är den önskade lösningen och den andra är en tvetydig lösning. Ytterligare information begränsar ofta möjligheterna till en unik plats. I tredimensionell geometri, när det är känt att en punkt ligger på ytorna av tre sfärer, ger de tre sfärernas mittpunkter tillsammans med deras radier också tillräcklig information för att begränsa de möjliga platserna till högst två (om inte centrum ligger på en rak linje).

True-range multilateration kan jämföras med den mer frekventa påträffade pseudo-range multilateration , som använder avståndsskillnader för att lokalisera en (typiskt rörlig) punkt. Pseudoområdesmultilatering implementeras nästan alltid genom att mäta ankomsttider (TOA) för energivågor. True-range multilateration kan också jämföras med triangulering , vilket innebär mätning av vinklar .

Terminologi

Det finns ingen accepterad eller allmänt använd allmän term för vad som kallas multilateration med sanna intervall här . Det namnet är valt för att det: (a) är en korrekt beskrivning och delvis bekant terminologi ( multilatering används ofta i detta sammanhang); (b) undviker att specificera antalet inblandade intervall (som t.ex. räckviddsintervall gör ; (c) undviker att antyda en applikation (liksom t.ex. DME/DME-navigering eller trilaterering ) och (d) och undviker förväxling med de fler vanlig pseudo-range multilateration .

Erhålla intervall

För liknande räckvidder och mätfel ger ett navigations- och övervakningssystem baserat på multilateration med sann räckvidd service till ett betydligt större 2D-område eller 3D-volym än system baserade på pseudo- räckviddsmultilateration . Det är dock ofta svårare eller dyrare att mäta sant=intervall än det är att mäta pseudointervall. För avstånd upp till några mil och fasta platser kan sann räckvidd mätas manuellt. Detta har gjorts inom lantmäteri i flera tusen år – till exempel med hjälp av rep och kedjor.

För längre avstånd och/eller rörliga fordon behövs i allmänhet ett radio/radarsystem. Denna teknik utvecklades först cirka 1940 i samband med radar. Sedan dess har tre metoder använts:

Tvåvägs avståndsmätning, en part aktiv – Detta är metoden som används av traditionella radar (ibland kallad primärradar ) för att bestämma räckvidden för ett icke-samarbetande mål, och som nu används av laseravståndsmätare . Dess huvudsakliga begränsningar är att: (a) målet inte identifierar sig självt, och i en situation med flera mål kan feltilldelning av en retur inträffa; (b) retursignalen dämpas (i förhållande till den sända signalen) med fjärde potensen av fordonsstationsräckvidden (sålunda, för avstånd på tiotals mil eller mer kräver stationer i allmänhet högeffektsändare och/eller stora/känsliga antenner); och (c) många system använder siktlinjeutbredning, vilket begränsar deras räckvidd till mindre än 20 miles när båda parter är på liknande höjder över havet.
Tvåvägs räckviddsmätning, båda parter aktiva – Denna metod användes enligt uppgift först för navigering av flygledningssystemet Y -Gerät som sattes in 1941 av Luftwaffe. Den används nu globalt inom flygtrafikledning – t.ex. sekundär radarövervakning och DME/DME-navigering. Det kräver att båda parter har både sändare och mottagare, och kan kräva att störningsproblem åtgärdas.
Envägsavståndsmätning – Flygtiden ( TOF) för elektromagnetisk energi mellan flera stationer och fordonet mäts baserat på sändning av en part och mottagning av den andra. Detta är den senast utvecklade metoden och möjliggjordes av utvecklingen av atomur ; det kräver att fordonet (användaren) och stationerna har synkroniserade klockor. Det har framgångsrikt demonstrerats (experimentellt) med Loran-C och GPS.

Lösningsmetoder

True-range multilaterationsalgoritmer kan partitioneras baserat på

problemutrymmesdimension (vanligtvis två eller tre),
problemrumsgeometri (i allmänhet kartesisk eller sfärisk) och
förekomst av redundanta mätningar (mer än problemutrymmesdimensionen).

Alla pseudo-range multilateration algoritmer kan specialiseras för användning med true-range multilateration.

Två kartesiska dimensioner, två uppmätta lutningsområden (trilateration)

Fig. 1 2-D Cartesian true-range multilateration (trilateration) scenario. C1 och C2 är mittpunkter för cirklar med känd separation

U

. P är punkt vars

(x,y)

koordinater önskas baserat på

U

och uppmätta intervall

r_{1}

och

r_{ 2}

.

En analytisk lösning har sannolikt varit känd i över 1 000 år och ges i flera texter. Dessutom kan man enkelt anpassa algoritmer för ett tredimensionellt kartesiskt utrymme.

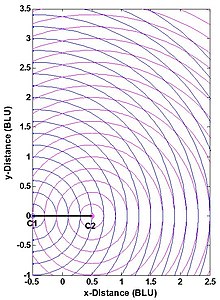
Den enklaste algoritmen använder analytisk geometri och en stationsbaserad koordinatram. Betrakta således cirkelcentrumen (eller stationerna) Cl och C2 i fig. 1 som har kända koordinater (t.ex. redan har undersökts) och vars separation $U$ är känd. Figuren 'sida' innehåller C1 och C2 . Om en tredje 'intressepunkt' P (t.ex. ett fordon eller en annan punkt som ska undersökas) är vid okänd punkt $(x,y)$ så ger Pythagoras sats

{\begin{aligned}r_{1}^{2}&=x^{2}+y^{ 2}\\[4pt]r_{2}^{2}&=(Ux)^{2}+y^{2}\end{aligned}}

Således,

${\begin{aligned}x&={\frac {r_{1}^{2}-r_{2 }^{2}+U^{2}}{2U}}\\[4pt]y&=\pm {\sqrt {r_{1}^{2}-x^{2}}}\end{aligned} }$

()

Observera att $y$ har två värden (dvs lösningen är tvetydig); detta brukar inte vara ett problem.

Även om det finns många förbättringar, är ekvation 1 det mest grundläggande multilaterationsförhållandet med sanna intervall. Flygplans DME/DME-navigering och trilaterationsmetoden för mätning är exempel på dess tillämpning. Under andra världskriget Oboe och under Koreakriget använde SHORAN samma princip för att styra flygplan baserat på uppmätta avstånd till två markstationer. SHORAN användes senare för oljeprospektering till havs och för flygmätning. Det australiensiska Aerodist flygundersökningssystemet använde 2D Cartesian true-range multilateration. Detta 2D-scenario är tillräckligt viktigt för att termen trilateration ofta används för alla tillämpningar som involverar en känd baslinje och två mätningar av avstånd.

Baslinjen som innehåller cirklarnas mittpunkter är en symmetrilinje. De korrekta och tvetydiga lösningarna är vinkelräta mot och lika långt från (på motsatta sidor av) baslinjen. Vanligtvis är den tvetydiga lösningen lätt att identifiera. Till exempel, om P är ett fordon, kommer varje rörelse mot eller bort från baslinjen att vara motsatt den för den tvetydiga lösningen; sålunda räcker det med ett grovt mått på fordonets kurs. Ett andra exempel: lantmätare är väl medvetna om vilken sida av baslinjen som P ligger. Ett tredje exempel: i applikationer där P är ett flygplan och C1 och C2 är på marken, är den tvetydiga lösningen vanligtvis under jord.

Om det behövs kan de inre vinklarna för triangeln C1-C2-P hittas med hjälp av den trigonometriska lagen för cosinus . Vid behov kan koordinaterna för P också uttryckas i ett andra, mer känt koordinatsystem – t.ex. Universal Transverse Mercator (UTM)-systemet – förutsatt att koordinaterna för C1 och C2 är kända i det andra systemet. Båda görs ofta i lantmäteri när trilatereringsmetoden används. När koordinaterna för P är etablerade kan linjerna C1-P och C2-P användas som nya baslinjer och ytterligare punkter undersökas. Sålunda kan stora områden eller avstånd övervakas baserat på flera, mindre trianglar – kallad travers .

Ett underförstått antagande för att ovanstående ekvation ska vara sann är att $r_{1}$ och $r_{2}$ relaterar till samma position av P . När P är ett fordon måste vanligtvis $r_{1}$ och $r_{2}$ mätas inom en synkroniseringstolerans som beror på fordonets hastighet och det tillåtna fordonets positionsfel. Alternativt kan fordonsrörelser mellan avståndsmätningar redovisas, ofta genom dödräkning.

En trigonometrisk lösning är också möjlig (side-side-side case). En lösning som använder grafik är också möjlig. En grafisk lösning används ibland under realtidsnavigering, som en överlagring på en karta.

Tre kartesiska dimensioner, tre uppmätta lutningsområden

Fig. 2 3-D True-Range Multilaterationsscenario. C1, C2 och C3 är kända centra för sfärer i x,y-planet. P är punkt vars (x,y,z) koordinater önskas baserat på dess intervall till C1, C2 och C3.

3-D Tri- lateration begränsar de potentiella positionerna till två (här A eller B)

Det finns flera algoritmer som löser det 3-D kartesiska multilaterationsproblemet med sanna intervall direkt (dvs i sluten form) – t.ex. Fang. Dessutom kan man använda slutna algoritmer utvecklade för multilateration av pseudointervall . Bancrofts algoritm (anpassad) använder vektorer, vilket är en fördel i vissa situationer.

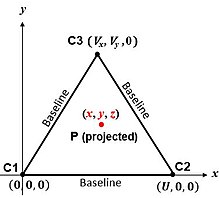
Den enklaste algoritmen motsvarar sfärcentrumen i Fig. 2. Figuren 'sida' är planet som innehåller C1 , C2 och C3 . Om P är en 'intressant plats' (t.ex. fordon) vid $(x,y,z)$ , så ger Pythagoras sats lutningsintervallen mellan P och sfärens mittpunkter:

{\begin{aligned}r_{1}^{2}&=x^{2}+y^{2}+z^{2}\\[4pt]r_{2}^{2}& =(xU)^{2}+y^{2}+z^{2}\\[4pt]r_{3}^{2}&=(x-V_{x})^{2}+(y -V_{y})^{2}+z^{2}\end{aligned}}

är koordinaterna för P :

${\begin{aligned}x&={\frac {r_{1}^{2}-r_{2}^{2}+U^{2}}{2U}}\\[4pt]y& ={\frac {r_{1}^{2}-r_{3}^{2}+V_{x}^{2}+V_{y}^{2}-2V_{x}x}{2V_{ y}}}\\[4pt]z&=\pm {\sqrt {r_{1}^{2}-x^{2}-y^{2}}}\end{aligned}}$

()

Planet som innehåller sfärens centra är ett symmetriplan. De korrekta och tvetydiga lösningarna är vinkelräta mot den och lika långt från den, på motsatta sidor.

Många tillämpningar av 3D-multilatering med sanna intervall involverar korta avstånd – t.ex. precisionstillverkning. Integrering av avståndsmätning från tre eller fler radarer (t.ex. FAA:s ERAM ) är en 3-D flygplansövervakningsapplikation. 3-D true-range multilateration har använts på experimentbasis med GPS-satelliter för flygplansnavigering. Kravet på att ett flygplan ska vara utrustat med ett atomur utesluter dess allmänna användning. GPS-mottagarens klockhjälp är dock ett område för aktiv forskning, inklusive hjälp över ett nätverk. Därmed kan slutsatserna ändras. 3-D true-range multilateration utvärderades av International Civil Aviation Organization som ett flygplanslandningssystem, men en annan teknik visade sig vara mer effektiv. Att noggrant mäta flygplanets höjd under inflygning och landning kräver många markstationer längs flygbanan.

Två sfäriska dimensioner, två eller flera uppmätta sfäriska intervall

Fig. 3 Exempel på höjdskärningsproblem för himmelsnavigering (positionslinjer förvrängs av kartprojektionen)

Detta är ett klassiskt himmelskt (eller astronomiskt) navigeringsproblem, kallat höjdskärningsproblemet ( Fig . 3). Det är den sfäriska geometrin som motsvarar trilaterationsmetoden för mätning (även om avstånden i allmänhet är mycket större). En lösning till havs (som inte nödvändigtvis involverar solen och månen) möjliggjordes av den marina kronometern (introducerades 1761) och upptäckten av 'positionslinjen' (LOP) 1837. Lösningsmetoden som nu lärs ut mest vid universitet ( t.ex. US Naval Academy) använder sfärisk trigonometri för att lösa en sned sfärisk triangel baserad på sextantmätningar av "höjden" för två himmelska kroppar. Detta problem kan också lösas med hjälp av vektoranalys. Historiskt har grafiska tekniker – t.ex. interceptmetoden – använts. Dessa kan ta emot mer än två uppmätta "höjder". På grund av svårigheten att göra mätningar till sjöss rekommenderas ofta 3 till 5 'höjder'.

Eftersom jorden är bättre modellerad som en rotationsellipsoid än en sfär, kan iterativa tekniker användas i moderna implementeringar. I flygplan och missiler på hög höjd är ett himmelsnavigeringsundersystem ofta integrerat med ett tröghetsnavigeringsundersystem för att utföra automatiserad navigering - t.ex. US Air Force SR-71 Blackbird och B-2 Spirit .

Även om Loran-C är avsett som ett "sfäriskt" multilaterationssystem för pseudointervall, har Loran-C också använts som ett "sfäriskt" multilaterationssystem med sant omfång av välutrustade användare (t.ex. Canadian Hydrographic Service). Detta gjorde det möjligt att utöka täckningsområdet för en Loran-C stationstriad avsevärt (t.ex. fördubblas eller tredubblas) och det minsta antalet tillgängliga sändare att reduceras från tre till två. I modern luftfart mäts lutande intervall snarare än sfäriska intervaller oftare; men när flygplanets höjd är känd, omvandlas lutande avstånd lätt till sfäriska avstånd.

Redundanta räckviddsmätningar

När det finns fler räckviddsmätningar tillgängliga än det finns problemdimensioner, antingen från samma C1 och C2 (eller C1 , C2 och C3 ) stationer, eller från ytterligare stationer, uppnås åtminstone dessa fördelar:

"Dåliga" mätningar kan identifieras och förkastas
Tvetydiga lösningar kan identifieras automatiskt (dvs utan mänsklig inblandning) -- kräver en extra station
Fel i "bra" mätningar kan beräknas i medeltal, vilket minskar deras effekt.

Den iterativa Gauss-Newton-algoritmen för att lösa problem med icke-linjära minsta kvadrater (NLLS) är i allmänhet att föredra när det finns fler "bra" mätningar än vad som krävs. En viktig fördel med Gauss-Newton-metoden jämfört med många slutna algoritmer är att den behandlar räckviddsfel linjärt, vilket ofta är deras natur, och minskar därmed effekten av räckviddsfel genom medelvärdesbildning. Gauss-Newton-metoden kan också användas med det minsta antalet uppmätta intervall. Eftersom den är iterativ kräver Gauss-Newton-metoden en initial lösningsuppskattning.

I 3-D kartesiska rymden eliminerar en fjärde sfär den tvetydiga lösningen som uppstår med tre intervall, förutsatt att dess centrum inte är i samma plan som de första tre. I 2D kartesiskt eller sfäriskt rymd eliminerar en tredje cirkel den tvetydiga lösningen som uppstår med två intervall, förutsatt att dess centrum inte är kolinjärt med de två första.

Engångsapplikation kontra repetitiv applikation

Den här artikeln beskriver till stor del "engångs"-tillämpning av multilaterationstekniken med sanna intervall, vilket är den mest grundläggande användningen av tekniken. Med hänvisning till fig. 1 är kännetecknet för "engångs"-situationer att punkten P och åtminstone en av Cl och C2 ändras från en tillämpning av multilaterationstekniken med sanna intervall till nästa. Detta är lämpligt för kartläggning, himmelsnavigering med manuella iakttagelser och vissa flygplans DME/DME-navigering.

I andra situationer tillämpas emellertid multilaterationstekniken med sanna intervall repetitivt (i huvudsak kontinuerligt). I dessa situationer C1 och C2 (och kanske Cn, n = 3,4,... ) konstanta och P är samma vehikel. Exempel på tillämpningar (och utvalda intervall mellan mätningar) är: övervakning av flera radarflygplan (5 och 12 sekunder, beroende på radartäckningsräckvidd), flygmätning, Loran-C-navigering med en användarklocka med hög noggrannhet (ungefär 0,1 sekunder) och några flygplans DME/DME-navigering (ungefär 0,1 sekunder). Generellt gäller implementeringar för upprepad användning: (a) använder en "spårningsalgoritm" (utöver multilaterationslösningsalgoritmen), som gör det möjligt att jämföra mätningar som samlats in vid olika tidpunkter och beräknas medelvärde på något sätt; och (b) använder en iterativ lösningsalgoritm, eftersom de (bl) tillåter varierande antal mätningar (inklusive redundanta mätningar) och (b2) i sig har en initial gissning varje gång lösningsalgoritmen anropas.

Hybrid multilaterationssystem

Hybrid multilaterationssystem – de som varken är system för äkta intervall eller pseudo intervall – är också möjliga. Till exempel, i fig. 1, om cirkelns mittpunkter förskjuts åt vänster så att C1 är vid $x_{1}^{\prime }=-{ \tfrac {1}{2}}U,y_{1}^{\prime }=0$ och C2 är vid $x_{2}^{\prime }={\tfrac {1}{2}}U,y_{2}^{\prime }=0$ då är intressepunkten P vid

{\begin{aligned}x^{\prime }&={\frac {(r_{1}^{\prime }+r_{2}^{\prime })(r_{ 1}^{\prime }-r_{2}^{\prime })}{2U}}\\[4pt]y^{\prime }&=\pm {\frac {{\sqrt {(r_{1 }^{\prime }+r_{2}^{\prime })^{2}-U^{2}}}{\sqrt {U^{2}-(r_{1}^{\prime }- r_{2}^{\prime })^{2}}}}{2U}}\end{aligned}}

Denna form av lösningen beror uttryckligen på summan och skillnaden av $r_{1}^{\prime }$ och $r_{2}^{\prime }$ och kräver inte 'kedja' från $x^{\prime }$ -lösningen till $y^{\prime }$ -lösningen. Det skulle kunna implementeras som ett multilaterationssystem med sanna intervall genom att mäta $r_{1}^{\prime }$ och $r_{2}^{\prime }$ .

Det skulle dock också kunna implementeras som ett hybrid multilaterationssystem genom att mäta $r_{1}^{\prime }+r_{2}^{\prime }$ och $r_{1}^{\prime }-r_{2}^{\prime }$ med annan utrustning – t.ex. för övervakning av en multistatisk radar med en sändare och två mottagare (snarare än två monostatiska radarer ) . Även om det är en fördel att eliminera en sändare, finns det en motverkande "kostnad": synkroniseringstoleransen för de två stationerna blir beroende av utbredningshastigheten (vanligtvis ljusets hastighet) snarare än hastigheten för punkten P , för att exakt mäta både $r_{1}^{\prime }\pm r_{2}^{\prime }$ .

Även om de inte har implementerats operativt har hybrid multilaterationssystem undersökts för flygplansövervakning nära flygplatser och som backupsystem för GPS-navigering för flyg.

Preliminära och slutliga beräkningar

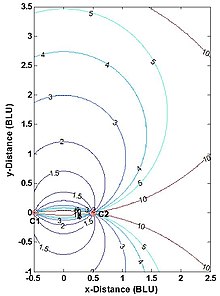
Fig. 4 2D-system för avståndsmätningar för multilateration (trilateration) med sanna intervall

Positionsnoggrannheten för ett multilaterationssystem med sanna intervall – t.ex. noggrannheten för ${\displaystyle (x,y)}-$ koordinaterna för punkt P i fig. 1 – beror på två faktorer: (1) intervallet mätnoggrannhet, och (2) det geometriska förhållandet mellan P och systemets stationer C1 och C2 . Detta kan förstås från fig. 4. De två stationerna visas som punkter, och BLU betecknar baslinjeenheter. (Mätmönstret är symmetriskt om både baslinjen och den vinkelräta bisektrisen av baslinjen, och är trunkerad i figuren.) Som vanligt görs antas individuella avståndsmätfel vara oberoende av avstånd, statistiskt oberoende och identiskt fördelade. Detta rimliga antagande separerar effekterna av användarstationsgeometri och avståndsmätningsfel på felet i de beräknade ( $\displaystyle (x,y)}-$ koordinaterna för P . Här är mätgeometrin helt enkelt den vinkel vid vilken två cirklar korsar - eller motsvarande vinkeln mellan linjerna P-C1 och P-C2 . När punkt P- inte är på en cirkel är felet i dess position ungefär proportionellt mot området som begränsas av de två närmaste blåa och de närmaste två magenta cirklarna.

Utan redundanta mätningar kan ett multilaterationssystem med sanna intervall inte vara mer exakt än räckviddsmätningarna, men kan vara betydligt mindre exakt om mätgeometrin inte väljs korrekt. Följaktligen sätter vissa tillämpningar restriktioner på platsen för punkt P. För en 2D kartesisk situation (trilateration) tar dessa begränsningar en av två likvärdiga former:

Den tillåtna inre vinkeln vid P mellan linjerna P-C1 och P-C2 : Idealet är en rät vinkel, som uppstår på avstånd från baslinjen på en halv eller mindre av baslinjens längd; maximalt tillåtna avvikelser från de ideala 90 graderna kan anges.
Den horisontella utspädningen av precision (HDOP), som multiplicerar avståndsfelet vid bestämning av positionsfelet: För två dimensioner är den ideala (minsta) HDOP kvadratroten av 2 ( 2 ≈ 1,414 {\ $sqrt {2}} \approx 1,414}$ ), vilket uppstår när vinkeln mellan P-C1 och P-C2 är 90 grader; ett maximalt tillåtet HDOP-värde kan anges. (Här är lika HDOPs helt enkelt platsen för punkter i fig. 4 som har samma korsningsvinkel.)

Fig. 5 HDOP-konturer för ett 2D-system för multilateration (trilateration) med sanna intervall

Att planera ett system för navigering eller övervakning med flera sidor med sanna avstånd innebär ofta en utspädning av precisionsanalys (DOP) för att informera beslut om antalet och placeringen av stationerna och systemets serviceområde (två dimensioner) eller servicevolym (tre dimensioner). Fig. 5 visar horisontella DOP:er (HDOPs) för ett 2-D, tvåstations multilaterationssystem med sanna intervall. HDOP är oändlig längs baslinjen och dess förlängningar, eftersom endast en av de två dimensionerna faktiskt mäts. En användare av ett sådant system bör vara ungefär bredsidan av baslinjen och inom ett applikationsberoende intervallband. Till exempel, för DME/DME-navigeringsfixar med flygplan, är den maximala HDOP som tillåts av US FAA två gånger det lägsta möjliga värdet, eller 2,828, vilket begränsar det maximala användningsintervallet (som inträffar längs baslinjehalveringslinjen) till 1,866 gånger baslinjelängden . (Planet som innehåller två DME-markstationer och ett flygplan är inte strikt horisontellt, men är vanligtvis nästan så.) På liknande sätt väljer lantmätare punkt P i Fig. 1 så att C1-C2-P ungefär bildar en liksidig triangel (där HDOP = 1,633) ).

Fel i trilaterationsundersökningar diskuteras i flera dokument. I allmänhet läggs tonvikten på effekterna av räckviddsmätningsfel snarare än på effekterna av numeriska algoritmfel.

Ansökningar

Lantmäteri med hjälp av trilaterationsmetoden
Flygmätning
Sjöarkeologisk lantmäteri
DME/DME RNAV flygplansnavigering
Multipel radarintegration (t.ex. FAA ERAM )
Himmelsnavigering med höjdskärningsmetoden
Intercept-metod — Grafisk lösning på problemet med höjdavlyssning
Kalibrering av laserinterferometrar
SHORAN , Oboe , Gee-H — Flygplansledningssystem utvecklade för "blinda" bombningar
JTIDS ( Joint Tactical Information Distribution System ) -- USA/NATO-system som (bland andra möjligheter) lokaliserar deltagare i ett nätverk med hjälp av inter-deltagarintervall
USAF SR-71 Blackbird flygplan—Använder astro-tröghetsnavigering
USAF B-2 Spirit- flygplan—Använder astro-tröghetsnavigering
Experimentell Loran-C-teknik

För- och nackdelar för fordonsnavigering och övervakning

Navigation och övervakningssystem involverar vanligtvis fordon och kräver att en statlig enhet eller annan organisation distribuerar flera stationer som använder en form av radioteknik (dvs. använder elektromagnetiska vågor). Fördelarna och nackdelarna med att använda äkta multilateration för ett sådant system visas i följande tabell.

Fördelar	Nackdelar
Stationsplatser är flexibla; de kan placeras centralt eller perifert Noggrannheten försämras långsamt med avståndet från stationen (i allmänhet bättre än multilateration med pseudoområde) Kräver en station färre än ett multilaterationssystem för pseudointervall Stationssynkronisering är inte krävande (baserat på hastighet av intressepunkt, och kan åtgärdas genom död räkning )	Ofta krävs att en användare har både en sändare och en mottagare Noggrannheten i det kooperativa systemet är känslig för vändningsfel i utrustningen Kan inte användas för smygövervakning Icke-samarbetsvillig övervakning innebär vägförluster till fjärde potensen av avstånd

True-range multilateration kontrasteras ofta med (pseudo range) multilateration, eftersom båda kräver en form av användarintervall till flera stationer. Komplexiteten och kostnaden för användarutrustning är sannolikt den viktigaste faktorn för att begränsa användningen av multilateration med äkta räckvidd för fordonsnavigering och övervakning. Vissa användningar är inte det ursprungliga syftet med systeminstallation – t.ex. DME/DME-flygplansnavigering.

Se även

Avståndsgeometriproblem , liknande teknik tillämpad på molekyler
Himmelsnavigering — uråldrig navigeringsteknik baserad på himmelska kroppar
Avståndsmätningsutrustning (DME) -- System som används för att mäta avståndet mellan ett flygplan och en markstation
Euklidiskt avstånd
Intercept-metod — Grafisk teknik som används vid himmelsnavigering
Laseravståndsmätare
Multilateration – Adresserar multilateration av pseudointervall
Avståndsmätare — System som används för att mäta avståndet mellan två punkter på marken
Resektion (orientering)
SHORAN —Utvecklat som ett militärt flygnavigeringssystem, senare använt för civila ändamål
Undersökande
Tellurometer — Första elektroniska mikrovågsavståndsmätare
Triangulering – Mätmetod baserad på mätning av vinklar

externa länkar

stackexchange.com , PHP / Python-implementering