Trilinjär interpolation

Trilinjär interpolation är en metod för multivariat interpolation på ett 3-dimensionellt regelbundet rutnät . Den approximerar värdet av en funktion vid en mellanliggande punkt $(x,y,z)$ inom det lokala axiella rektangulära prismat linjärt, med hjälp av funktionsdata på gitterpunkterna. För ett godtyckligt, ostrukturerat nät (som används i finita elementanalys) måste andra interpolationsmetoder användas; om alla nätelement är tetraedrar (3D- simpliceringar ) ger barycentriska koordinater en enkel procedur.

Trilinjär interpolation används ofta i numerisk analys , dataanalys och datorgrafik .

Jämfört med linjär och bilinjär interpolation

Trilinjär interpolation är förlängningen av linjär interpolation , som fungerar i utrymmen med dimension $D=1$ , och bilinjär interpolation , som fungerar med dimension $D=2$ , till dimension $D=3$ . Dessa interpolationsscheman använder alla polynom av ordning 1, vilket ger en noggrannhet av ordning 2, och det kräver $2^{D}=8$ intilliggande fördefinierade värden som omger interpolationspunkten. Det finns flera sätt att komma fram till trilinjär interpolation, vilket är ekvivalent med 3-dimensionell tensor B-spline interpolation av ordning 1, och den trilinjära interpolationsoperatorn är också en tensorprodukt av 3 linjära interpolationsoperatorer.

Metod

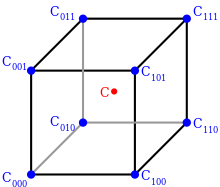
Åtta hörnpunkter på en kub som omger interpolationspunkten C

Skildring av 3D-interpolation

En geometrisk visualisering av trilinjär interpolation. Produkten av värdet vid den önskade punkten och hela volymen är lika med summan av produkterna av värdet vid varje hörn och delvolymen diagonalt mitt emot hörnet.

På ett periodiskt och kubiskt gitter, låt $x_{\text{d}}$ , $y_{\text{d}}$ och $z_{\text{d }}$ vara skillnaderna mellan var och en av $x$ , $y$ , $z$ och den mindre koordinatrelaterade, det vill säga:

${\begin{aligned}x_{\text{d}}={\ frac {x-x_{0}}{x_{1}-x_{0}}}\\y_{\text{d}}={\frac {y-y_{0}}{y_{1}-y_ {0}}}\\z_{\text{d}}={\frac {z-z_{0}}{z_{1}-z_{0}}}\end{aligned}}$

där $x_{0}$ indikerar gitterpunkten under $x$ , och $x_{1}$ indikerar gitterpunkten ovanför $x$ och på liknande sätt för $y_{0},y_{1},z_{0}$ och $z_{1}$ .

Först interpolerar vi längs $x$ (föreställ dig att vi "skjuter" ytan på kuben definierad av $C_{0jk}$ till den motsatta ytan, definierad av $C_ {1jk}$ ), vilket ger:

${\begin{aligned}c_{00}&=c_{000}(1-x_{\text{d}})+c_{100} x_{\text{d}}\\c_{01}&=c_{001}(1-x_{\text{d}})+c_{101}x_{\text{d}}\\c_{10 }&=c_{010}(1-x_{\text{d}})+c_{110}x_{\text{d}}\\c_{11}&=c_{011}(1-x_{\ text{d}})+c_{111}x_{\text{d}}\end{aligned}}$

Där $c_{000}}$$(x_{0},y_{0},z_{0}).$ betyder funktionsvärdet för Sedan interpolerar vi dessa värden (längs $y$ , "pushing" från $C_{i0k}$ till $C_{i1k}$ ), vilket ger:

${\begin{aligned}c_{0}&=c_{00} (1-y_{\text{d}})+c_{10}y_{\text{d}}\\c_{1}&=c_{01}(1-y_{\text{d}})+ c_{11}y_{\text{d}}\end{aligned}}$

Slutligen interpolerar vi dessa värden längs $z$ (genom en linje):

$c=c_{0}(1-z_{\text{d}})+c_{1}z_{\text{d}}.$

Detta ger oss ett förutsagt värde för punkten.

Resultatet av trilinjär interpolation är oberoende av ordningen för interpolationsstegen längs de tre axlarna: vilken annan ordning som helst, till exempel längs $x$ , sedan längs $y$ , och slutligen längs $z$ , ger samma värde.

Ovanstående operationer kan visualiseras enligt följande: Först hittar vi de åtta hörnen av en kub som omger vår intressanta plats. Dessa hörn har värdena $c_{000}$ , $c_{100}$ , $c_{010}$ , $c_{110}$ , $c_{001}$ , $c_{101}$ , $c_{011}$ , $c_{111}$ .

Därefter utför vi linjär interpolation mellan $c_{000}$ och $c_{100}$ för att hitta ${\displaystyle c_{00}} ,$ c $\displaystyle c_{001} }$ och $c_{101}$ för att hitta $c_{01}$ , $c_{011}$ och $c_{111}$ för att hitta $c_{11}$ , $c_{010}$ och $c_{110}$ för att hitta $c_{10}$ .

Nu gör vi interpolation mellan $c_{00}$ och $c_{10}$ för att hitta ${\displaystyle c_{0}} ,$ c $\displaystyle c_{01}}$ och $c_{11}$ för att hitta $c_{1}$ . Slutligen beräknar vi värdet $c$ via linjär interpolation av $c_{0}$ och $c_{1}$

I praktiken är en trilinjär interpolation identisk med två bilinjär interpolation kombinerad med en linjär interpolation:

$c\approx l\left(b(c_{000} ,c_{010},c_{100},c_{110}),\,b(c_{001},c_{011},c_{101},c_{111})\right)$

Alternativ algoritm

Ett alternativt sätt att skriva lösningen på interpolationsproblemet är

$f(x, y,z)\approx a_{0}+a_{1}x+a_{2}y+a_{3}z+a_{4}xy+a_{5}xz+a_{6}yz+a_{7 }xyz$

där koefficienterna hittas genom att lösa det linjära systemet

${\begin{aligned} {\begin{bmatrix}1&x_{0}&y_{0}&z_{0}&x_{0}y_{0}&x_{0}z_{0}&y_{0}z_{0}&x_{0}y_{0} z_{0}\\1&x_{1}&y_{0}&z_{0}&x_{1}y_{0}&x_{1}z_{0}&y_{0}z_{0}&x_{1}y_{0} z_{0}\\1&x_{0}&y_{1}&z_{0}&x_{0}y_{1}&x_{0}z_{0}&y_{1}z_{0}&x_{0}y_{1} z_{0}\\1&x_{1}&y_{1}&z_{0}&x_{1}y_{1}&x_{1}z_{0}&y_{1}z_{0}&x_{1}y_{1} z_{0}\\1&x_{0}&y_{0}&z_{1}&x_{0}y_{0}&x_{0}z_{1}&y_{0}z_{1}&x_{0}y_{0} z_{1}\\1&x_{1}&y_{0}&z_{1}&x_{1}y_{0}&x_{1}z_{1}&y_{0}z_{1}&x_{1}y_{0} z_{1}\\1&x_{0}&y_{1}&z_{1}&x_{0}y_{1}&x_{0}z_{1}&y_{1}z_{1}&x_{0}y_{1} z_{1}\\1&x_{1}&y_{1}&z_{1}&x_{1}y_{1}&x_{1}z_{1}&y_{1}z_{1}&x_{1}y_{1} z_{1}\end{bmatrix}}{\begin{bmatrix}a_{0}\\a_{1}\\a_{2}\\a_{3}\\a_{4}\\a_{5} \\a_{6}\\a_{7}\end{bmatrix}}={\begin{bmatrix}c_{000}\\c_{100}\\c_{010}\\c_{110}\\c_ {001}\\c_{101}\\c_{011}\\c_{111}\end{bmatrix}},\end{aligned}}$

ger resultatet

${\begin{aligned}a_{0}={}&{\frac {-c_{000}x_{1}y_{1}z_{1}+c_{001}x_{1}y_{1 }z_{0}+c_{010}x_{1}y_{0}z_{1}-c_{011}x_{1}y_{0}z_{0}}{(x_{0}-x_{1 })(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\\&{\frac {c_{100}x_{0}y_{1}z_{ 1}-c_{101}x_{0}y_{1}z_{0}-c_{110}x_{0}y_{0}z_{1}+c_{111}x_{0}y_{0}z_ {0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{1} ={}&{\frac {c_{000}y_{1}z_{1}-c_{001}y_{1}z_{0}-c_{010}y_{0}z_{1}+c_{011 }y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\ \&{\frac {-c_{100}y_{1}z_{1}+c_{101}y_{1}z_{0}+c_{110}y_{0}z_{1}-c_{111} y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt ]a_{2}={}&{\frac {c_{000}x_{1}z_{1}-c_{001}x_{1}z_{0}-c_{010}x_{1}z_{1 }+c_{011}x_{1}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})} }+{}\\&{\frac {-c_{100}x_{0}z_{1}+c_{101}x_{0}z_{0}+c_{110}x_{0}z_{1} -c_{111}x_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}} ,\\[4pt]a_{3}={}&{\frac {c_{000}x_{1}y_{1}-c_{001}x_{1}y_{1}-c_{010}x_{ 1}y_{0}+c_{011}x_{1}y_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_ {1})}}+{}\\&{\frac {-c_{100}x_{0}y_{1}+c_{101}x_{0}y_{1}+c_{110}x_{0 }y_{0}-c_{111}x_{0}y_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{ 1})}},\\[4pt]a_{4}={}&{\frac {-c_{000}z_{1}+c_{001}z_{0}+c_{010}z_{1} -c_{011}z_{0}+c_{100}z_{1}-c_{101}z_{0}-c_{110}z_{1}+c_{111}z_{0}}{(x_{ 0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{5}=&{\frac {-c_ {000}y_{1}+c_{001}y_{1}+c_{010}y_{0}-c_{011}y_{0}+c_{100}y_{1}-c_{101}y_{ 1}-c_{110}y_{0}+c_{111}y_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}- z_{1})}},\\[4pt]a_{6}={}&{\frac {-c_{000}x_{1}+c_{001}x_{1}+c_{010}x_{ 1}-c_{011}x_{1}+c_{100}x_{0}-c_{101}x_{0}-c_{110}x_{0}+c_{111}x_{0}}{( x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{7}={}&{\ frac {c_{000}-c_{001}-c_{010}+c_{011}-c_{100}+c_{101}+c_{110}-c_{111}}{(x_{0}-x_ {1})(y_{0}-y_{1})(z_{0}-z_{1})}}.\end{aligned}}$

Se även

• Linjär interpolation
• Bilinjär interpolation
• Trikubisk interpolation
• Radiell interpolation
• Tetraedrisk interpolation
• Sfärisk linjär interpolation

externa länkar

• pseudo-kod från NASA , beskriver en iterativ invers trilinjär interpolation (med tanke på hörnen och värdet på C hittar Xd, Yd och Zd).
• Paul Bourke, Interpolation methods , 1999. Innehåller en mycket smart och enkel metod för att hitta trilinjär interpolation som är baserad på binär logik och som kan utökas till vilken dimension som helst (Tetralinjär, Pentalinjär, ...).
• Kenwright, Free-Form Tetrahedron Deformation. Internationellt symposium om visuell datoranvändning. Springer International Publishing, 2015 [1] .