B-spline

Splinekurva ritad som en viktad summa av B-splines med kontrollpunkter/kontrollpolygon och markerade komponentkurvor

I det matematiska underområdet för numerisk analys är en B-spline eller basisspline en splinefunktion som har minimalt stöd med avseende på en given grad , jämnhet och domänpartition . Varje splinefunktion av given grad kan uttryckas som en linjär kombination av B-splines av den graden. Cardinal B-splines har knutar som är lika långt från varandra. B-splines kan användas för kurvanpassning och numerisk differentiering av experimentella data.

I datorstödd design och datorgrafik är splinefunktioner konstruerade som linjära kombinationer av B-splines med en uppsättning kontrollpunkter.

Introduktion

Termen "B-spline" myntades av Isaac Jacob Schoenberg och är en förkortning för basisspline . En splinefunktion av ordningen $n$ är en bitvis polynomfunktion av grad $n-1$ i en variabel $x$ . Platserna där bitarna möts kallas för knutar. Nyckelegenskapen för splinefunktioner är att de och deras derivator kan vara kontinuerliga, beroende på mångfalden av knutarna.

B-splines av ordningen $n$ är basfunktioner för splinefunktioner av samma ordning definierade över samma knutar, vilket innebär att alla möjliga splinefunktioner kan byggas från en linjär kombination av B-splines, och det finns bara en unik kombination för varje splinefunktion.

Definition

Kardinal kvadratisk B-spline med knutvektor (0, 0, 0, 1, 2, 3, 3, 3) och kontrollpunkter (0, 0, 1, 0, 0), och dess första derivata

Kardinal kubisk B-spline med knutvektor (−2, −2, −2, −2, −1, 0, 1, 2, 2, 2, 2) och kontrollpunkter (0, 0, 0, 6, 0, 0, 0), och dess första derivata

Kardinal kvarts B-spline med knutvektor (0, 0, 0, 0, 0, 1, 2, 3, 4, 5, 5, 5, 5, 5) och kontrollpunkter (0, 0, 0, 0, 1 , 0, 0, 0, 0), och dess första och andra derivator

En spline av ordningen $n$ är en styckvis polynomfunktion av grad $n-1$ i en variabel $x$ . Värdena på $x$ där delarna av polynomet möts är kända som knutar, betecknade $t_{0},t_{1},t_{2} ,\ldots ,t_{n}$ och sorterade i icke-minskande ordning. När knutarna är distinkta är de första $n-2$ derivatorna av polynombitarna kontinuerliga över varje knut. När $r$ -knutarna är sammanfallande, är endast de första $nr-1$ -derivatorna av spline kontinuerliga över den knuten.

För en given sekvens av knop finns det, upp till en skalningsfaktor, en unik spline $B_{i,n}(x)$ som uppfyller

$B_{i,n}(x)={\begin{cases}0&{\text{if }}x<t_{i}{\text{ eller }}x\geq t_{i+n}, \\{\text{icke-noll}}&{\text{annars}}.\end{case}}$

Om vi ​​lägger till den ytterligare begränsningen som $\sum _{i}B_{i,n}(x)=1$ för alla $x$ mellan den första och sista knuten, då blir skalfaktorn för ${\displaystyle B_{i,n}(x)} fast.$ De resulterande $B_{i,n}(x)$ splinefunktionerna kallas B-splines.

Alternativt kan B-splines definieras genom konstruktion med hjälp av Cox–de Boors rekursionsformel. Givet en knutsekvens $\ldots ,t_{0},t_{1},t_{2},\ldots$ , definieras B-splines av ordning 1 av

$B_{i,1}(x):={\begin{cases}1&{\text{if }}t_{i}\leq x<t_{i+1},\\0&{\text{ annars}}.\end{cases}}$

Dessa uppfyller $\sum _{i}B_{i,1}(x)=1$ för alla $x$ eftersom för alla $x$ exakt en av ${\displaystyle B_{i,1}(x)=1} ,$ och alla andra är noll.

De högre ordningens B-splines definieras av rekursion

$_ \displaystyle B_{i,k+1}(x):=\omega _{i,k}(x)B_{i,k}(x)+[1-\omega _{i+1,k}( x)]B_{i+1,k}(x),}$

var

$\omega _{i,k}(x):={\begin{cases}{\dfrac {x-t_{i}}{t_{i+k}-t_{i}}},&t_{ i+k}\neq t_{i},\\0&{\text{annars}}.\end{cases}}$

Egenskaper

En B-spline-funktion är en kombination av flexibla band som styrs av ett antal punkter som kallas kontrollpunkter, vilket skapar jämna kurvor. Dessa funktioner används för att skapa och hantera komplexa former och ytor med hjälp av ett antal punkter. B-spline-funktion och Bézier-funktioner används i stor utsträckning i formoptimeringsmetoder.

En B-spline av ordningen $n$ är en styckvis polynomfunktion av grad $n-1$ i en variabel $x$ . Den definieras över $1+n$ platser $t_{j}$ , kallade knutar eller brytpunkter, som måste vara i icke-fallande ordning $t_ {j}\leq t_{j+1}$ . B-spline bidrar endast i intervallet mellan den första och sista av dessa knutar och är noll på andra ställen. Om varje knut är separerad med samma avstånd $h$ (där $h=t_{j+1}-t_{j}$ ) från sin föregångare, kommer knuten vektor och motsvarande B-splines kallas "uniform" (se kardinal B-spline nedan).

För varje ändligt knutintervall där det inte är noll är en B-spline ett polynom med graden $n-1$ . En B-spline är en kontinuerlig funktion vid knutarna. När alla knutar som hör till B-spline är distinkta, är dess derivator också kontinuerliga upp till derivatan av graden $n-2$ . Om knutarna är sammanfallande vid ett givet värde på $x$ reduceras kontinuiteten i derivatordern med 1 för varje ytterligare sammanfallande knut. B-splines kan dela en delmängd av sina knutar, men två B-splines definierade över exakt samma knutar är identiska. Med andra ord, en B-spline definieras unikt av sina knutar.

Man skiljer på inre knutar och ändpunkter. Interna knutar täcker $x$ -domänen man är intresserad av. Eftersom en enda B-spline redan sträcker sig över $1+n$ knop, följer det att de interna knutarna behöver förlängas med $n-1$ ändpunkter på varje sida, för att ge fullt stöd åt den första och sista B-spline, vilket påverkar de interna knutintervallen. Värdena på ändpunkterna spelar ingen roll, vanligtvis upprepas den första eller sista inre knuten bara.

Användbarheten med B-splines ligger i det faktum att vilken splinefunktion som helst av ordningen $n$ på en given uppsättning knutar kan uttryckas som en linjär kombination av B-splines:

$S_{n,\mathbf {t} }(x)=\summa _{i}\alpha _{i}B_{i,n}(x).$

B-splines spelar rollen som basfunktioner för splinefunktionsutrymmet, därav namnet. Denna egenskap följer av att alla delar har samma kontinuitetsegenskaper, inom sitt individuella stödområde, vid knutarna.

Uttryck för polynombitarna kan härledas med hjälp av Cox–de Boors rekursionsformel

$B_{i,0}(x):={\begin{cases}1&{\text{if }}t_{i}\leq x<t_{i+1},\\0&{\text{ annars}}.\end{fall}}$

$B_{i,k}(x):={\frac {x-t_{i}}{t_{i+k}-t_{i}}}B_{i,k-1}(x) +{\frac {t_{i+k+1}-x}{t_{i+k+1}-t_{i+1}}}B_{i+1,k-1}(x).$

Det vill säga, $B_{j,0}(x)$ är styckvis konstant ett eller noll, vilket indikerar vilket knopspann x är i (noll om knopspan j upprepas). Rekursionsekvationen är i två delar:

${\frac {x-t_{i}}{t_{i+k}-t_{i}}}$

rampar från noll till ett när x går från $t_{i}$ till ${\displaystyle t_{i+k}} ,$ och

${\frac {t_{i+k+1}-x}{t_{i+k+1}-t_{i +1}}}$

ramper från ett till noll när x går från $t_{i+1}$ till $t_{i+k+1}$ . Motsvarande B är noll utanför dessa respektive intervall. Till exempel $B_{i,1}(x)$ en triangulär funktion som är noll under $x=t_{i}$ , rampar till ett vid $x=t_{i+1}$ och tillbaka till noll vid och bortom $x=t_{i+2}$ . Men eftersom B-spline-basfunktioner har lokalt stöd , beräknas B-splines vanligtvis av algoritmer som inte behöver utvärdera basfunktioner där de är noll, såsom de Boors algoritm .

Denna relation leder direkt till den FORTRAN -kodade algoritmen BSPLV, som genererar värden för B-splines av ordningen n vid x . Följande schema illustrerar hur varje del av ordningen n är en linjär kombination av delarna av B-splines av ordningen n − 1 till vänster.

${\begin{matrix}&&0\\&0&\\0&B_{i-2, 2}\\&B_{i-1,1}&\\B_{i,0}&&B_{i-1,2}\\&B_{i,1}&\\0&&B_{i,2}\\&0&\ \&&0\end{matris}}$

Tillämpning av rekursionsformeln med knutarna vid $\displaystyle (0,1,2,3)}$ ger delarna av den enhetliga B-spline av ordning 3

${\begin{aligned}B_{1}&=x^{2}/2,&0&\leq x<1,\\B_{2}&=(-2x^{2}+ 6x-3)/2,&1&\leq x<2,\\B_{3}&=(3-x)^{2}/2,&2&\leq x<3.\end{aligned}}$

Dessa bitar visas i diagrammet. Kontinuitetsegenskapen för en kvadratisk splinefunktion och dess första derivata vid de inre knutarna illustreras enligt följande

${\begin{aligned}&{\text{At }}x=1\colon \ B_{1}=B_{2}=0.5,\ {\frac {dB_{1}} {dx}}={\frac {dB_{2}}{dx}}=1.\\[6pt]&{\text{At }}x=2\colon \ B_{2}=B_{3}= 0.5,\ {\frac {dB_{2}}{dx}}={\frac {dB_{3}}{dx}}=-1.\end{aligned}}$

Den andra derivatan av en B-spline av grad 2 är diskontinuerlig vid knutarna:

${\frac {d^{2}B_{1}}{ dx^{2}}}=1,\ {\frac {d^{2}B_{2}}{dx^{2}}}=-2,\ {\frac {d^{2}B_{3 }}{dx^{2}}}=-1.$

Snabbare varianter av de Boor-algoritmen har föreslagits, men de lider av jämförelsevis lägre stabilitet.

Kardinal B-spline

En kardinal B-spline har ett konstant avstånd h mellan knutarna. Kardinal B-splines för en given ordning n är bara förskjutna kopior av varandra. De kan erhållas från den enklare definitionen.

$B_{i,n,t}(x)={\frac {x-t_{i}}{h}}n[0,\dots ,n](\cdot -t_{i})_{ +}^{n-1}.$

"Placeholder"-notationen används för att indikera att den n -: e delade skillnaden för funktionen $(tx)_{+}^{n-1}$ av de två variablerna t och x ska tas genom att fixera x och betrakta $(tx)_{+}^{n-1}$ som en funktion av enbart t .

En kardinal B-spline har jämnt fördelade knutar, därför är interpolering mellan knutarna lika med faltning med en utjämnande kärna.

Exempel, om vi vill interpolera tre värden mellan B-spline noder ( ${\textbf {b}}$ ), kan vi skriva signalen som

$\mathbf {x} =[\mathbf {b} _{1},0,0,\mathbf {b} _{2},0,0,\mathbf {b} _{3},0, 0,\dots ,\mathbf {b} _{n},0,0].$

Konvolution av signalen $\mathbf {x}$ med en rektangelfunktion $\mathbf {h} =[1/3,1/3 ,1/3]$ ger första ordningens interpolerade B-spline-värden. Andra ordningens B-spline-interpolation är faltning med en rektangelfunktion två gånger $\mathbf {y} =\mathbf {x} *\mathbf {h} *\mathbf {h}$ ; genom iterativ filtrering med en rektangelfunktion erhålls interpolation av högre ordning.

Snabb B-spline-interpolering på en enhetlig provdomän kan göras genom iterativ medelfiltrering. Alternativt är en rektangelfunktion lika med sinc i Fourier-domänen . Därför är kubisk spline-interpolation lika med multiplicering av signalen i Fourier-domänen med sinc ⁴ .

Se Irwin–Hall distribution#Specialfall för algebraiska uttryck för kardinal B-splines av grad 1–4.

P-spline

Termen P-spline står för "straffad B-spline". Det hänvisar till att använda B-spline-representationen där koefficienterna bestäms dels av de data som ska monteras , och dels av en extra strafffunktion som syftar till att införa jämnhet för att undvika överanpassning .

Två- och flerdimensionella P-spline-approximationer av data kan använda den ansiktsdelande produkten av matriser för att minimera beräkningsoperationer.

Härledda uttryck

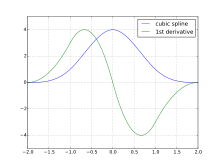
Derivatan av en B-spline av grad k är helt enkelt en funktion av B-splines av grad k − 1:

${\frac {dB_{i,k}(x)}{dx}}=k\left({\frac {B_{i,k-1}(x)}{t_{i+k}- t_{i}}}-{\frac {B_{i+1,k-1}(x)}{t_{i+k+1}-t_{i+1}}}\right).$

Detta betyder att

${\frac {d}{dx}}\sum _{i}\alpha _{i}B_{i,k}=\summa _{i=r-k+2}^{s -1}k{\frac {\alpha _{i}-\alpha _{i-1}}{t_{i+k}-t_{i}}}B_{i,k-1}\quad {\ text{on}}\quad [t_{r},t_{s}],$

vilket visar att det finns ett enkelt samband mellan derivatan av en splinefunktion och B-splines av grad en mindre.

Moment av univariata B-splines

$p(x)$ för att representera 1-d sannolikhetstäthetsfunktioner . Ett exempel är en viktad summa av $i$ B-spline basfunktioner av ordningen ${\displaystyle n} ,$ som var och en är areanormaliserade till enhet (dvs. inte direkt utvärderade med standard de-Boor-algoritmen)

$p(x)=\summa _{i}c_{i}\cdot B_{i,n,{\textbf {norm }}}(x)$

och med normaliseringskonstant begränsning $\sum _{i}c_{i}=1$ . Det k -:te råmomentet $\mu _{k}$ för en normaliserad B-spline $B_{i,n,{\textbf {norm}}}$ kan vara skrivet som Carlsons Dirichlet-medelvärde $R_{k}$ , vilket i sin tur kan lösas exakt via en konturintegral och en iterativ summa som

$\mu _{k}=R_{k}(\mathbf {m} ;\mathbf {t} )=\int _{-\infty }^{\infty }x^{k}\cdot B_{i,n,{\textbf {norm}}}(x\mid t_{1}\dots t_{j})\,dx={\frac {\Gamma (k+ 1)\Gamma (m)}{\Gamma (m+k)}}\cdot D_{k}(\mathbf {m} ,\mathbf {t} )$

med

$D_{k}={\frac {1}{k}}\summa \ limits _{u=1}^{k}\left[\left(\sum \limits _{i=1}^{j}m_{i}\cdot {t_{i}}^{u}\right) D_{ku}\right]$

och $D_{0}=1$ . Här $\mathbf {t}$ en vektor med $j$ -knutpositionerna och $\mathbf {m}$ en vektor med respektive knutmultiplikheter. Man kan därför beräkna vilket moment som helst av en sannolikhetstäthetsfunktion $p(x)$ representerad av summan av B-spline basfunktioner exakt, utan att tillgripa numeriska tekniker.

Förhållande till styckvis/sammansatt Bézier

En Bézier-kurva är också en polynomkurva som kan definieras med en rekursion från kurvor av lägre grader av samma klass och kodad i termer av kontrollpunkter, men en viktig skillnad är att alla termer i rekursionen för ett Bézier-kurvsegment har samma domän av definition (vanligtvis $[0,1]$ ), medan stöden för de två termerna i B-splinerekursionen är olika (de yttersta delintervallen är inte vanliga). Detta betyder att en Bézier-kurva av grad $n$ given av $m\gg n$ kontrollpunkter består av ungefär $m/n$ mestadels oberoende segment, medan B- spline med samma parametrar övergår smidigt från delintervall till delintervall. För att få något jämförbart från en Bézier-kurva skulle man behöva införa ett jämnhetsvillkor på övergångar mellan segment, vilket resulterar i något sätt av Bézier-spline (för vilken många kontrollpunkter skulle bestämmas av jämnhetskravet).

En bitvis/sammansatt Bézier-kurva är en serie Bézier-kurvor sammanfogade med åtminstone C0-kontinuitet (den sista punkten i en kurva sammanfaller med startpunkten för nästa kurva). Beroende på applikation kan ytterligare krav på jämnhet (som C1- eller C2-kontinuitet) läggas till. C1 kontinuerliga kurvor har identiska tangenter vid brytpunkten (där de två kurvorna möts). C2 kontinuerliga kurvor har identisk krökning vid brytpunkten.

Kurvanpassning

Vanligtvis vid kurvanpassning är en uppsättning datapunkter utrustade med en kurva som definieras av någon matematisk funktion. Till exempel använder vanliga typer av kurvanpassning ett polynom eller en uppsättning exponentialfunktioner . När det inte finns någon teoretisk grund för att välja en passningsfunktion kan kurvan förses med en splinefunktion som består av summan av B-splines, med metoden minsta kvadrater . Sålunda objektivfunktionen för minsta kvadraters minimering, för en splinefunktion av grad k ,

$U=\summa _{{\text{all}}~ x}\left\{W(x)\left[y(x)-\summa _{i}\alpha _{i}B_{i,k,t}(x)\höger]\höger\}^{ 2},$

där W ( x ) är en vikt och y ( x ) är referensvärdet vid x . Koefficienterna $\alpha _{i}$ är de parametrar som ska bestämmas. Knutvärdena kan vara fasta eller behandlas som parametrar.

Den största svårigheten med att tillämpa denna process är att bestämma antalet knop som ska användas och var de ska placeras. de Boor föreslår olika strategier för att lösa detta problem. Till exempel minskas avståndet mellan knoparna i proportion till krökningen (2:a derivatan) av datan. Ett fåtal ansökningar har publicerats. Till exempel har användningen av B-splines för att passa enkla Lorentziska och Gaussiska kurvor undersökts. Optimala splinefunktioner av graderna 3–7 inklusive, baserade på symmetriska arrangemang av 5, 6 och 7 knop, har beräknats och metoden användes för utjämning och differentiering av spektroskopiska kurvor. I en jämförbar studie gav den tvådimensionella versionen av Savitzky-Golay-filtreringen och splinemetoden bättre resultat än glidande medelvärde eller Chebyshev-filtrering .

Datorstödd design och datorgrafik

I datorstödd design och datorgrafikapplikationer representeras en splinekurva ibland som ${\displaystyle C(t)} ,$ en parametrisk kurva för någon verklig parameter $t$ . I detta fall kan kurvan $C(t)$ behandlas som två eller tre separata koordinatfunktioner $(x(t),y(t) ))$ , eller $(x(t),y(t),z(t))$ . Koordinatfunktionerna $x(t)$ , $y(t)$ och $z(t)$ är var och en splinefunktion, med en gemensam uppsättning av knutvärden $t_{1},t_{2},\ldots ,t_{n}$ .

Eftersom en B-splines bildar basfunktioner kan var och en av koordinatfunktionerna uttryckas som en linjär summa av B-splines, så vi har

${\begin{aligned}X(t)&=\summa _{i}x_{i}B_{i,n}(t),\\Y(t)&=\summa _{i}y_ {i}B_{i,n}(t),\\Z(t)&=\sum _{i}z_{i}B_{i,n}(t).\end{aligned}}$

Vikterna $x_{i}$ , $displaystyle y_{i}}$${\displaystyle P_{i}=(x_{i},y_{i},z_{i})} i$ och $z_{i}$ kan kombineras för att bilda punkter 3-d rymd. Dessa punkter $P_{i}$ är allmänt kända som kontrollpunkter.

Om du arbetar i omvänd riktning, definierar en sekvens av kontrollpunkter, knutvärden och ordningen för B-spline en parametrisk kurva. Denna representation av en kurva med kontrollpunkter har flera användbara egenskaper:

1. Kontrollpunkterna $P_{i}$ definierar en kurva. Om kontrollpunkterna alla transformeras tillsammans på något sätt, som att translateras, roteras, skalas eller flyttas av någon affin transformation, så transformeras motsvarande kurva på samma sätt.
2. Eftersom B-splines är icke-noll för bara ett ändligt antal knopintervall, om en enda kontrollpunkt flyttas, är motsvarande ändring av den parametriska kurvan strax över parameterområdet för ett litet antal knopintervall.
3. Eftersom ${\displaystyle \sum _{i}B_{i,n}(x)=1} ,$ och hela tiden varje $B_{i,n}(x)\geq 0$ , då förblir kurvan innanför kontrollpunkternas begränsningsram. Även i någon mening följer kurvan i stort sett kontrollpunkterna.

En mindre önskvärd egenskap är att den parametriska kurvan inte interpolerar kontrollpunkterna. Vanligtvis går kurvan inte genom kontrollpunkterna.

NURBS

Huvudartikel: Olikformig rationell B-spline

NURBS-kurva – polynomkurva definierad i homogena koordinater (blå) och dess projektion på plan – rationell kurva (röd)

Inom datorstödd design , datorstödd tillverkning och datorgrafik är en kraftfull förlängning av B-splines olikformiga rationella B-splines (NURBS). NURBS är i huvudsak B-splines i homogena koordinater . Liksom B-splines, definieras de av sin ordning, och en knutvektor och en uppsättning kontrollpunkter, men till skillnad från enkla B-splines har kontrollpunkterna var och en en vikt. När vikten är lika med 1 är en NURBS helt enkelt en B-spline och som sådan generaliserar NURBS både B-splines och Bézier-kurvor och -ytor, den primära skillnaden är viktningen av kontrollpunkterna som gör NURBS-kurvorna "rationella".

Genom att utvärdera en NURBS vid olika värden av parametrarna kan kurvan spåras genom rymden; på samma sätt, genom att utvärdera en NURBS-yta vid olika värden av de två parametrarna, kan ytan representeras i kartesisk rymd.

Precis som B-splines bestämmer NURBS-kontrollpunkter kurvans form. Varje punkt i kurvan beräknas genom att ta en viktad summa av ett antal kontrollpunkter. Vikten av varje punkt varierar beroende på den styrande parametern. För en kurva av grad d , är påverkan av en kontrollpunkt endast från noll i d +1 intervall (knutspann) av parameterutrymmet. Inom dessa intervall ändras vikten enligt en polynomfunktion (basfunktioner) av grad d . Vid gränserna för intervallen går basfunktionerna jämnt till noll, jämnheten bestäms av graden av polynomet.

Knutvektorn är en sekvens av parametervärden som bestämmer var och hur kontrollpunkterna påverkar NURBS-kurvan. Antalet knop är alltid lika med antalet kontrollpunkter plus kurvgrad plus en. Varje gång parametervärdet går in i ett nytt knopspann, blir en ny kontrollpunkt aktiv, medan en gammal kontrollpunkt kasseras.

En NURBS-kurva har följande form:

$C(u)={\frac {\sum _ {i=1}^{k}N_{i,n}(u)w_{i}P_{i}}{\sum _{i=1}^{k}N_{i,n}(u)w_ {i}}}$

Här är notationen som följer. u är den oberoende variabeln (istället för x ), k är antalet kontrollpunkter, N är en B-spline (används istället för B ), n är polynomgraden, P är en kontrollpunkt och w är en vikt. Nämnaren är en normaliserande faktor som utvärderas till en om alla vikter är en.

Det är vanligt att skriva detta som

$C(u)=\sum _{i=1}^{k}R_{i,n}(u)P_{ i}$

där funktionerna

${\displaystyle R_{i,n}(u)={\frac {N_$

är kända som de rationella basfunktionerna.

En NURBS-yta erhålls som tensorprodukten av två NURBS-kurvor, och använder således två oberoende parametrar u och v (med index i respektive j ):

$^{ k}\sum _{j=1}^{\ell }R_{i,j}(u,v)P_{i,j}}$

med

$R_{i,j}(u,v)={\frac {N_{i,n}(u)N_{j,m}(v)w_{i,j}} {\sum _{p=1}^{k}\sum _{q=1}^{\ell }N_{p,n}(u)N_{q,m}(v)w_{p,q} }}$

som rationella grundfunktioner.

Se även

• Bézier-kurva
• Box spline
• De Boor algoritm
• I-spline
• M-spline
• Spline wavelet
• T-spline

Anteckningar

Anförda verk

•   Carl de Boor (1978). En praktisk guide till splines . Springer-Verlag. ISBN 978-3-540-90356-7 .
•   Piegl, Les; Tiller, Wayne (1997). The NURBS Book (2:a upplagan). Springer. ISBN 978-3-540-61545-3 .

Vidare läsning

•   Richard H. Bartels; John C. Beatty; Brian A. Barsky (1987). En introduktion till splines för användning i datorgrafik och geometrisk modellering . Morgan Kaufmann. ISBN 978-1-55860-400-1 .
• Jean Gallier (1999). Kurvor och ytor i geometrisk modellering: teori och algoritmer . Morgan Kaufmann. Kapitel 6. B-Spline-kurvor. Denna bok är slutsåld och fritt tillgänglig från författaren.
•   Hartmut Prautzsch; Wolfgang Boehm; Marco Paluszny (2002). Bézier och B-Spline-tekniker . Springer Science & Business Media. ISBN 978-3-540-43761-1 .
•   David Salomon (2006). Kurvor och ytor för datorgrafik . Springer. Kapitel 7. B-Spline Approximation. ISBN 978-0-387-28452-1 .
• Hovey, Tchad (2022). Formulering och Python-implementering av Bézier och B-Spline Geometry. SAND2022-7702C . (153 sidor)

externa länkar

• Weisstein, Eric W. "B-Spline" . MathWorld .
• Ruf, Johannes. "B-splines av tredje ordningen på ett olikformigt rutnät" ( PDF) . Arkiverad från originalet (PDF) 2013-11-06 . Hämtad 2012-05-02 .
• bivariat B-spline från numpy
• Interaktiva B-splines med JSXGraph
• TinySpline: Opensource C-bibliotek med bindningar för olika språk
• Enhetliga icke-rationella B-Splines, modellering av kurvor i 2D-rymden. Författare:Stefan G. Beck
• B-Spline Editor av Shukant Pal