Styv ekvation

I matematik är en styv ekvation en differentialekvation för vilken vissa numeriska metoder för att lösa ekvationen är numeriskt instabila , om inte stegstorleken tas för att vara extremt liten. Det har visat sig svårt att formulera en exakt definition av styvhet, men huvudtanken är att ekvationen innehåller några termer som kan leda till snabb variation i lösningen.

När man integrerar en differentialekvation numeriskt skulle man förvänta sig att den erforderliga stegstorleken är relativt liten i ett område där lösningskurvan uppvisar mycket variation och vara relativt stor där lösningskurvan rätar ut för att närma sig en linje med lutning nästan noll. För vissa problem är detta inte fallet. För att en numerisk metod ska ge en tillförlitlig lösning på differentialsystemet krävs ibland att stegstorleken är på en oacceptabelt liten nivå i ett område där lösningskurvan är mycket jämn. Fenomenet är känt som stelhet . I vissa fall kan det finnas två olika problem med samma lösning, men det ena är inte stelt och det andra är det. Fenomenet kan därför inte vara en egenskap hos den exakta lösningen, eftersom denna är densamma för båda problemen, och måste vara en egenskap hos själva differentialsystemet. Sådana system kallas därför stela system .

Motiverande exempel

Explicita numeriska metoder som uppvisar instabilitet när en styv vanlig differentialekvation integreras

Tänk på problemet med initialvärde

$\,y'(t)=-15y(t),\quad t\geq 0,\quad y( 0)=1.$

 

 

 

 

()

Den exakta lösningen (visas i cyan) är

$y(t)=e^{-15t},\quad y(t)\to 0{\text{ as }}t\to \infty .$

 

 

 

 

()

Vi söker en numerisk lösning som uppvisar samma beteende.

Figuren (höger) illustrerar de numeriska frågorna för olika numeriska integratörer som tillämpas på ekvationen.

1. Eulers metod med stegstorleken $h={\tfrac {1}{4}}$ oscillerar vilt och lämnar snabbt grafens intervall (visas i rött).
2. Eulers metod med halva stegstorleken, ${\displaystyle h={\tfrac {1}{8}}} ,$ ger en lösning inom grafens gränser, men svänger omkring noll (visas i grönt).
3. Den trapetsformade metoden (det vill säga tvåstegs Adams–Moulton-metoden) ges av

   $y_{n+1}=y_{n}+ {\tfrac {1}{2}}h{\bigl (}f(t_{n},y_{n})+f(t_{n+1},y_{n+1}){\bigr )} ,$

    

    

    

    

   ()

   där $y'=f(t,y)$ . Att tillämpa denna metod istället för Eulers metod ger ett mycket bättre resultat (blått). De numeriska resultaten minskar monotont till noll, precis som den exakta lösningen gör.

Ett av de mest framträdande exemplen på de styva vanliga differentialekvationerna (ODEs) är ett system som beskriver Robertsons kemiska reaktion :

${\alignedstyle {\begin punkt {x}}&=-0.04x+10^{4}y\cdot z\\{\dot {y}}&=0.04x-10^{4}y\cdot z-3\cdot 10^{ 7}y^{2}\\{\dot {z}}&=3\cdot 10^{7}y^{2}\end{aligned}}}$

 

 

 

 

()

Om man behandlar detta system med ett kort intervall, till exempel, $t\in [0,40]$ är det inga problem med numerisk integration. Men om intervallet är mycket stort (säg 10 ¹¹ ), så kan många standardkoder inte integrera det korrekt.

Ytterligare exempel är uppsättningarna av ODE som är ett resultat av den tidsmässiga integrationen av stora kemiska reaktionsmekanismer. Här uppstår stelheten från samexistensen av mycket långsamma och mycket snabba reaktioner. För att lösa dem kan mjukvarupaketen KPP och Autochem användas.

Styvhetsförhållande

Betrakta den linjära konstantkoefficienten inhomogena systemet

$\mathbf {y} '=\mathbf {A} \mathbf {y} +\mathbf {f} (x),$

 

 

 

 

()

där $\mathbf {y} ,\mathbf {f} \in \mathbb {R} ^{n}$ och $\mathbf {A}$ är en konstant, diagonaliserbar, $n\ gånger n$ matris med egenvärden $\lambda _{t}\in \mathbb {C} ,t=1,2 ,\ldots ,n$ (antagna distinkta) och motsvarande egenvektorer $\mathbf {c} _{t}\in \mathbb {C} ^{n },t=1,2,\ldots ,n$ . Den allmänna lösningen av ( 5 ) har formen

$\mathbf {y} (x)=\sum _{t=1}^{n}\kappa _{t}e^{\lambda _{t}x}\mathbf {c} _{t}+\mathbf {g} (x),$

 

 

 

 

()

där $\kappa _{t}$ är godtyckliga konstanter och $\mathbf {g} (x)$ är en speciell integral. Låt oss nu anta det

$\operatorname {Re} (\lambda _{t})<0,\qquad t=1,2,\ldots ,n,$

 

 

 

 

()

vilket innebär att var och en av termerna $e^{\lambda _{t}x}\mathbf {c} _{t}\to 0$ som $x\ till \infty$ , så att lösningen $\mathbf {y} (x)$ närmar sig $\mathbf {g} (x)$ asymptotiskt som $x\till \infty$ ; termen $e^{\lambda _{t}x}\mathbf {c} _{t}$ kommer att förfalla monotont om $\lambda _{t}$ är verklig och sinusformigt om $\lambda _{t}$ är komplex.

Att tolka $x$ som tid (som det ofta är vid fysiska problem), ${\textstyle \sum _{t=1}^{n}\kappa _{t}e^{\lambda _{t}x}\mathbf {c} _{t}}$ kallas den transienta lösningen och $\mathbf {g} (x)$ den stabila- statlig lösning . Om $\left|\operatörsnamn {Re} (\lambda _{t})\right|$ är stor, då motsvarande term $\kappa _{t}e^{ \lambda _{t}x}\mathbf {c} _{t}$ kommer att avta snabbt när $x$ ökar och kallas därför en snabb transient ; om $\left|\operatörsnamn {Re} (\lambda _{t})\right|$ är liten, motsvarande term $\kappa _{t}e^{\ lambda _{t}x}\mathbf {c} _{t}$ sönderfaller långsamt och kallas en långsam transient . Låt ${\overline {\lambda }},{\underline {\lambda }}\in \{\lambda _{t },t=1,2,\ldots ,n\}$ definieras av

${\bigl |}\operatörsnamn {Re} ({\överlinje {\lambda }}){\bigr |}\geq {\bigl |}\operatörsnamn {Re} (\lambda _{t}){\bigr |}\geq {\bigl |}\operatörsnamn {Re} ({\underline {\lambda }}){\bigr |},\qquad t=1,2,\ ldots ,n$

 

 

 

 

()

så att $\kappa _{t}e^{{\overline {\lambda }}x}\mathbf {c} _{t}$ är den snabbaste transienten och ${\displaystyle \kappa _{t}e^{{\underline {\lambda }}x}\mathbf {c} _{t}} den långsammaste$ . Vi definierar nu styvhetsförhållandet som

${\frac {{\bigl |}\operatörsnamn {Re} ({\overline {\lambda }}){\bigr |}}{{\bigl |}\operatörsnamn {Re} ({\underline {\ lambda }}){\bigr |}}}.$

 

 

 

 

()

Karakterisering av stelhet

I det här avsnittet behandlar vi olika aspekter av fenomenet stelhet. "Fenomen" är förmodligen ett mer passande ord än "egenskap", eftersom det senare snarare antyder att styvhet kan definieras i exakta matematiska termer; det visar sig inte vara möjligt att göra detta på ett tillfredsställande sätt, även för den begränsade klassen av linjära konstantkoefficientsystem. Vi ska också se flera kvalitativa påståenden som kan göras (och mestadels har gjorts) i ett försök att kapsla in begreppet stelhet, och ange vad som förmodligen är det mest tillfredsställande av dessa som en "definition" av stelhet.

JD Lambert definierar styvhet enligt följande:

Om en numerisk metod med en ändlig region av absolut stabilitet , applicerad på ett system med några initiala villkor , tvingas använda i ett visst integrationsintervall en steglängd som är överdrivet liten i förhållande till jämnheten hos den exakta lösningen i det intervallet , då sägs systemet vara stelt i det intervallet.

Det finns andra egenskaper som uppvisas av många exempel på stelproblem, men för varje finns det motexempel, så dessa egenskaper gör inte bra definitioner av stelhet. Icke desto mindre är definitioner baserade på dessa egenskaper i vanligt bruk av vissa författare och är goda ledtrådar om förekomsten av stelhet. Lambert hänvisar till dessa som "uttalanden" snarare än definitioner, av ovannämnda skäl. Några av dessa är:

1. Ett linjärt konstant koefficientsystem är styvt om alla dess egenvärden har negativ reell del och styvhetsförhållandet är stort.
2. Styvhet uppstår när stabilitetskraven, snarare än de för noggrannhet, begränsar steglängden.
3. Stelhet uppstår när vissa komponenter i lösningen sönderfaller mycket snabbare än andra.

Etymologi

Ursprunget till termen "styvhet" har inte klarlagts. Enligt Joseph Oakland Hirschfelder används termen "styv" eftersom sådana system motsvarar tät koppling mellan föraren och driven i servomekanismer . Enligt Richard. L. Burden och J. Douglas Faires,

Betydande svårigheter kan uppstå när vanliga numeriska tekniker tillämpas för att approximera lösningen av en differentialekvation när den exakta lösningen innehåller termer av formen ${\displaystyle e^{\lambda t}} ,$ där $\lambda$ är ett komplext tal med negativ reell del.

. . .

Problem som involverar snabbt sönderfallande transienta lösningar förekommer naturligt i en mängd olika tillämpningar, inklusive studiet av fjäder- och dämpningssystem, analys av styrsystem och problem inom kemisk kinetik . Dessa är alla exempel på en klass av problem som kallas styva (matematisk styvhet) system av differentialekvationer, på grund av deras tillämpning vid analys av rörelsen hos fjäder- och masssystem som har stora fjäderkonstanter ( fysisk styvhet ) .

Till exempel initialvärdesproblemet

$m{\ddot {x}}+c{\dot {x}}+kx=0,\ qquad x(0)=x_{0},\qquad {\dot {x}}(0)=0,$

 

 

 

 

()

med $m=1$ , $c=1001$ , $k=1000$ , kan skrivas i formen ( 5 ) med $n=2$ och

$\mathbf {A} ={\begin{pmatrix}0&1\\-1000&-1001\end {pmatrix}},\qquad \mathbf {f} (t)={\begin{pmatrix}0\\0\end{pmatrix}},\qquad \mathbf {x} (0)={\begin{pmatrix} x_{0}\\0\end{pmatrix}},$

 

 

 

 

()

och har egenvärden ${\overline {\lambda }}=-1000,{\underline {\lambda }}=-1$ . Båda egenvärdena har negativ reell del och styvhetsförhållandet är

${\frac {|-1000|}{|-1|}}=1000,$

 

 

 

 

()

som är ganska stor. System ( 10 ) uppfyller då säkert påståendena 1 och 3. Här är fjäderkonstanten $k$ stor och dämpningskonstanten $c$ är ännu större. (medan "stor" inte är en tydligt definierad term, men ju större kvantiteterna ovan är, desto mer uttalad blir effekten av stelhet.) Den exakta lösningen på ( 10 ) är

$x(t)=x_{0}\left(-{\frac {1}{999}}e^{-1000t}+{\frac {1000}{999}}e^{-t}\ höger)\approx x_{0}e^{-t}.$

 

 

 

 

()

Ekvation 13 beter sig ganska likt en enkel exponentiell $x_{0}e^{-t}$ , men närvaron av termen ${\displaystyle e^{-1000t}} , t.o.m.$ med en liten koefficient, är tillräckligt för att göra den numeriska beräkningen mycket känslig för stegstorlek. Stabil integration av ( 10 ) kräver en mycket liten stegstorlek tills långt in i den jämna delen av lösningskurvan, vilket resulterar i ett fel som är mycket mindre än vad som krävs för noggrannhet. Systemet uppfyller således även påstående 2 och Lamberts definition.

A-stabilitet

$y(0)= 1$ stela problem kan analyseras genom att tillämpa dessa metoder på testekvationen $y'=ky$ under förutsättning att initialvillkoret med $k\in \mathbb {C}$ . Lösningen av denna ekvation är $y(t)=e^{kt}$ . Denna lösning närmar sig noll som $t\to \infty$ när $\operatorname {Re} (k)<0.$ Om den numeriska metoden också uppvisar detta beteende ( för en fast stegstorlek), sägs metoden vara A-stabil. En numerisk metod som är L-stabil (se nedan) har den starkare egenskapen att lösningen närmar sig noll i ett enda steg när stegstorleken går till oändlighet. A-stabila metoder uppvisar inte de instabilitetsproblem som beskrivs i det motiverande exemplet.

Runge–Kutta metoder

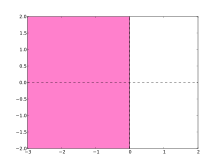
Runge–Kutta-metoder som tillämpas på testekvationen $y'=k\cdot y$ har formen $y_{n+1 }=\phi (hk)\cdot y_{n}$ , och, genom induktion, $y_{n}={\bigl (}\phi (hk) ){\bigr )}^{n}\cdot y_{0}$ . Funktionen $\phi$ kallas stabilitetsfunktionen . Således är villkoret att $y_{n}\to 0$ som $n\to \infty$ ekvivalent med $|\phi (hk)|<1$ . Detta motiverar definitionen av regionen med absolut stabilitet (ibland hänvisad till helt enkelt som stabilitetsregion ), som är mängden ${\bigl \{}z\in \mathbb {C} \,{\big |}\,|\phi (z)|<1{\bigr \}}$ . Metoden är A-stabil om regionen med absolut stabilitet innehåller mängden ${\bigl \{}z\in \mathbb {C} \,{\big |}\,\operatörsnamn {Re} (z)<0{\bigr \}}$ , det vill säga det vänstra halvplanet.

Exempel: Eulermetoderna

Den rosa skivan visar stabilitetsområdet för Eulermetoden.

Tänk på Euler-metoderna ovan. Den explicita Euler-metoden som tillämpas på testekvationen $y'=k\cdot y$ är

$y_{n+1}=y_{n}+h\cdot f(t_{n},y_{n})=y_{n}+h\cdot (ky_{n})=y_{n} +h\cdot k\cdot y_{n}=(1+h\cdot k)y_{n}.$

Därför är $y_{n}=(1+hk)^{n}\cdot y_{0}$$\phi (z)=1+z$ ϕ . Området för absolut stabilitet för denna metod är således ${\displaystyle {\bigl \{}z\in \mathbb {C} \,{\big |}\,|1+z|<1{\bigr \}}} som är disken som visas$ på höger. Eulermetoden är inte A-stabil.

Det motiverande exemplet hade $k=-15$ . Värdet på z när man tar stegstorlek $h={\tfrac {1}{4}}$ är ${\displaystyle z=-15\ gånger {\ tfrac {1}{4}}=-3.75} ,$ som är utanför stabilitetsområdet. Faktum är att de numeriska resultaten inte konvergerar till noll. Men med stegstorlek ${\displaystyle h={\tfrac {1}{8}}} ,$ har vi $z=-1,875$ som är precis innanför stabilitetsområdet och det numeriska resultaten konvergerar till noll, om än ganska långsamt.

Exempel: trapetsformad metod

Det rosa området är stabilitetsområdet för den trapetsformade metoden.

Tänk på den trapetsformade metoden

$y_{n+1}=y_{n} +{\tfrac {1}{2}}h\cdot {\bigl (}f(t_{n},y_{n})+f(t_{n+1},y_{n+1}){\ större )},$

när den tillämpas på testekvationen $y'=k\cdot y$ , är

$y_{n+1}=y_{n}+{\tfrac {1}{2}}h\cdot \left(ky_{n}+ky_{n+1}\right).$

Lösning för $y_{n+1}$ ger

$y_{n+1}={\frac {1+{\frac {1}{2}}hk}{1-{\frac {1}{2}}hk}}\cdot y_{n} .$

Således är stabilitetsfunktionen

$\phi (z)={\frac {1+{\frac {1}{2}}z}{1-{\frac {1 }{2}}z}}$

och regionen med absolut stabilitet är

$\left\{z\in \mathbb {C} \ \left|\ \left|{\frac {1+{\frac {1}{2}}z}{1-{\frac {1} {2}}z}}\right|<1\right.\right\}.$

Denna region innehåller det vänstra halvplanet, så den trapetsformade metoden är A-stabil. Faktum är att stabilitetsområdet är identiskt med det vänstra halvplanet, och därför konvergerar den numeriska lösningen av ${\displaystyle y'=k\cdot y} till noll om$ och bara om den exakta lösningen gör det. Ändå har den trapetsformade metoden inte perfekt beteende: den dämpar alla sönderfallande komponenter, men snabbt sönderfallande komponenter dämpas endast mycket milt, eftersom $\phi (z)\to 1$ som $z\to -\infty$ . Detta ledde till konceptet L-stabilitet : en metod är L-stabil om den är A-stabil och $|\phi (z)|\to 0$ som $z\to \infty$ . Den trapetsformade metoden är A-stabil men inte L-stabil. Den implicita Euler-metoden är ett exempel på en L-stabil metod.

Allmän teori

Stabilitetsfunktionen för en Runge–Kutta-metod med koefficienterna $\mathbf {A}$ och $\mathbf {b}$ ges av

$\phi (z)={\frac {\det \left(\mathbf {I} -z \mathbf {A} +z\mathbf {e} \mathbf {b} ^{\mathsf {T}}\right)}{\det(\mathbf {I} -z\mathbf {A} )}},$

där $\mathbf {e}$ anger vektorn med alla ettor. Detta är en rationell funktion (ett polynom dividerat med ett annat).

Explicita Runge–Kutta-metoder har en strikt lägre triangulär koefficientmatris $\mathbf {A}$ och därför är deras stabilitetsfunktion ett polynom. Det följer att explicita Runge–Kutta-metoder inte kan vara A-stabila.

Stabilitetsfunktionen hos implicita Runge–Kutta-metoder analyseras ofta med hjälp av ordningsstjärnor. Ordningsstjärnan för en metod med stabilitetsfunktion $\phi$ definieras som mängden ${\bigl \{}z\in \mathbb {C} \,{\big |}\,|\phi (z)|>|e^{z}|{\bigr \}}$ . En metod är A-stabil om och endast om dess stabilitetsfunktion inte har några poler i det vänstra planet och dess ordningsstjärna inte innehåller några rent imaginära tal.

Flerstegsmetoder

Linjära flerstegsmetoder har formen

$y_{n+1}=\sum _{i=0}^{s}a_{i}y_{ni}+h\summa _{j=-1}^{s}b_{j}f \left(t_{nj},y_{nj}\right).$

Tillämpade på testekvationen blir de

$y_{n+1}=\summa _{i=0}^ {s}a_{i}y_{ni}+hk\sum _{j=-1}^{s}b_{j}y_{nj},$

vilket kan förenklas till

$\left(1-b_{-1}z\right)y_{n +1}-\summa _{j=0}^{s}\left(a_{j}+b_{j}z\right)y_{nj}=0$

där $z=hk$ . Detta är ett linjärt återkommande förhållande . Metoden är A-stabil om alla lösningar $\{y_{n}\}$ av återfallsrelationen konvergerar till noll när $\operatorname {Re} (z) <0$ . Det karakteristiska polynomet är

$\Phi (z,w)=w^{s+1}-\sum _{i=0}^{s}a_{i}w^{si}-z\sum _{j=-1 }^{s}b_{j}w^{sj}.$

Alla lösningar konvergerar till noll för ett givet värde på $z$ om alla lösningar $w$ av $\Phi (z,w)=0$ ligger i enheten cirkel.

Området för absolut stabilitet för en flerstegsmetod av ovanstående form är då mängden av alla $z\in \mathbb {C}$ för vilka alla $w$ så att $\Phi (z,w)=0$ uppfyller $|w|<1$ . Återigen, om denna uppsättning innehåller det vänstra halvplanet, sägs flerstegsmetoden vara A-stabil.

Exempel: Andra ordningens Adams–Bashforth-metoden

Den rosa regionen är stabilitetsregionen för andra ordningens Adams–Bashforth-metoden.

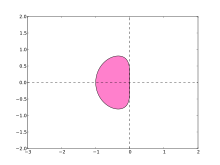
Låt oss bestämma området för absolut stabilitet för tvåstegs Adams–Bashforth-metoden

$y_{n+1}=y_{n}+h\left({\tfrac {3}{2}}f(t_{n},y_{n})-{\tfrac {1}{2 }}f(t_{n-1},y_{n-1})\höger).$

Det karakteristiska polynomet är

$\Phi (w,z)=w^{2}-\left(1+{\tfrac {3 }{2}}z\right)w+{\tfrac {1}{2}}z=0$

som har rötter

$w={\tfrac {1}{2}}\left(1+{\tfrac {3}{2} }z\pm {\sqrt {1+z+{\tfrac {9}{4}}z^{2}}}\right),$

sålunda är regionen med absolut stabilitet

$\left\{z\in \mathbb {C} \ \left|\ \left|{\tfrac {1}{2}}\left(1+{\tfrac {3}{2}}z\ pm {\sqrt {1+z+{\tfrac {9}{4}}z^{2}}}\right)\right|<1\right.\right\}.$

Denna region visas till höger. Den inkluderar inte hela det vänstra halvplanet (i själva verket inkluderar det bara den reella axeln mellan ${\displaystyle -1\leq z\leq 0} )$ så Adams–Bashforth-metoden är inte A-stabil.

Allmän teori

Explicita flerstegsmetoder kan aldrig vara A-stabila, precis som explicita Runge–Kutta-metoder. Implicita flerstegsmetoder kan bara vara A-stabila om deras ordning är högst 2. Det senare resultatet är känt som den andra Dahlquist -barriären; det begränsar användbarheten av linjära flerstegsmetoder för stela ekvationer. Ett exempel på en andra ordningens A-stabil metod är trapetsregeln som nämns ovan, som också kan betraktas som en linjär flerstegsmetod.

Se även

• Bakåtdifferentieringsformel , en familj av implicita metoder som speciellt används för att lösa stela differentialekvationer
• Villkorsnummer
• Differentialinkludering , en förlängning av begreppet differentialekvation som tillåter diskontinuiteter, delvis som ett sätt att kringgå vissa stelhetsproblem
• Explicita och implicita metoder

Anteckningar

•   Burden, Richard L.; Faires, J. Douglas (1993), Numerical Analysis (5:e upplagan), Boston: Prindle, Weber och Schmidt, ISBN 0-534-93219-3 .
• Dahlquist, Germund (1963 ) , "A special stabilitetsproblem for linear multistep methods", BIT , 3 (1): 27–43, doi : 10.1007/BF01963532 , hdl : 10338.dmlcz/103497 , S2C41 7 , S2CID   .
• Eberly, David (2008), Stabilitetsanalys för system av differentialekvationer (PDF) .
• Ehle, BL (1969), Om Padé-approximationer till exponentialfunktionen och A-stabila metoder för numerisk lösning av initialvärdeproblem ( PDF) , University of Waterloo .
• Gear, CW (1971), Numerical Initial-Value Problems in Ordinary Differential Equations , Englewood Cliffs: Prentice Hall , Bibcode : 1971nivp.book.....G .
• Gear, CW (1981), "Numerisk lösning av vanliga differentialekvationer: Finns det något kvar att göra?", SIAM Review , 23 (1): 10–24, doi : 10.1137/1023002 .
•   Hårare, Ernst; Wanner, Gerhard (1996), Solving ordinary differentialequations II: Stiff and differential-algebraic problems (andra upplagan), Berlin: Springer-Verlag , ISBN 978-3-540-60452-5 .
• Hirshfelder, JO (1963), "Applied Mathematics as used in Theoretical Chemistry", American Mathematical Society Symposium : 367–376 .
•   Iserles, Arieh; Nørsett, Syvert (1991), Order Stars , Chapman & Hall , ISBN 978-0-412-35260-7 .
•   Kreyszig, Erwin (1972), Advanced Engineering Mathematics (3:e upplagan), New York: Wiley , ISBN 0-471-50728-8 .
• Lambert, JD (1977), D. Jacobs (red.), "The initial value problem for ordinary differential equations", The State of the Art in Numerical Analysis , New York: Academic Press : 451–501 .
•   Lambert, JD (1992), Numerical Methods for Ordinary Differential Systems , New York: Wiley , ISBN 978-0-471-92990-1 .
• Mathews, John; Fink, Kurtis (1992), Numeriska metoder med MATLAB .
•   Tryck, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Avsnitt 17.5. Styva uppsättningar av ekvationer" . Numeriska recept: The Art of Scientific Computing (3:e upplagan). New York: Cambridge University Press. ISBN 978-0-521-88068-8 .
• Shampine, LF; Gear, CW (1979), "A user's view of solving stiff ordinary differential equations" , SIAM Review , 21 (1): 1–17, doi : 10.1137/1021001 .
•   Wanner, Gerhard; Hårare, Ernst; Nørsett, Syvert (1978), "Orderstjärnor och stabilitetsteori", BIT , 18 (4): 475–489, doi : 10.1007/BF01932026 , S2CID 8824105 .
• Stabilitet för Runge-Kutta-metoder [ 1]

externa länkar

• En introduktion till fysiskt baserad modellering: energifunktioner och styvhet
• Stela system Lawrence F. Shampine och Skip Thompson Scholarpedia , 2(3):2855. doi:10.4249/scholarpedia.2855