Stabilitetsradie

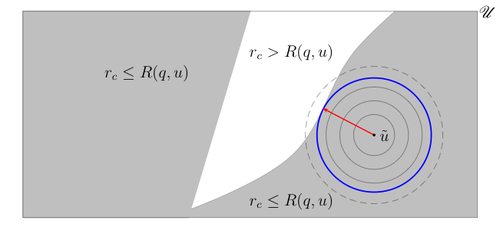
I matematik är stabilitetsradien för ett objekt (system, funktion , matris , parameter ) vid en given nominell punkt radien för den största kulan , centrerad vid den nominella punkten, vars alla element uppfyller förutbestämda stabilitetsvillkor. Bilden av denna intuitiva föreställning är denna:

där ${\hat {p}}$ anger den nominella punkten, $P$ anger utrymmet för alla möjliga värden för objektet $p$ , och det skuggade området, $P(s)$ , ​​representerar den uppsättning punkter som uppfyller stabilitetsvillkoren. Radien för den blå cirkeln, visad i rött, är stabilitetsradien.

Abstrakt definition

Den formella definitionen av detta begrepp varierar beroende på användningsområde. Följande abstrakta definition är ganska användbar

${\hat {\rho }}({\hat {p}} ):=\max \ \{\rho \geq 0:p\in P(s),\forall p\in B(\rho ,{\hat {p}})\}$

där $B(\rho ,{\hat {p}})$ anger en sluten boll med radien $\rho$ i $P$ centrerad på ${ \displaystyle {\hat {p}}}$ .

Historia

Det ser ut som att konceptet uppfanns i början av 1960-talet. På 1980-talet blev det populärt inom kontrollteori och optimering. Den används i stor utsträckning som en modell för lokal robusthet mot små störningar i ett givet nominellt värde för föremålet av intresse.

Relation till Walds maximin-modell

Det visades att stabilitetsradiemodellen är en instans av Walds maximin-modell . Det är,

$\max \ \ {\rho \geq 0:p\in P(s),\forall p\in B(\rho ,{\hat {p}})\}\equiv \max _{\rho \geq 0}\min _ {p\in B(\rho ,{\hat {p}})}f(\rho ,p)$

var

$f(\rho ,p)=\left\{{\begin{array}{cc}\ rho &,\ p\in P(s)\\-\infty &,\ p\notin P(s)\end{array}}\right.$

Det stora straffvärdet ( $-\infty$ ) är en anordning för att tvinga $\max$ -spelaren att inte störa det nominella värdet utanför systemets stabilitetsradie. Det är en indikation på att stabilitetsmodellen är en modell för lokal stabilitet/robusthet, snarare än en global.

Info-gap beslutsteori

Info-gap-beslutsteori är en nyligen icke-probabilistisk beslutsteori. Det påstås vara radikalt annorlunda än alla nuvarande teorier om beslut under osäkerhet. Men det har visat sig att dess robusthetsmodell, nämligen

${\hat {\alpha }}(q, {\tilde {u}}):=\max \ \{\alpha \geq 0:r_{c}\leq R(q,u),\forall u\in U(\alpha ,{\tilde {u} })\}$

är egentligen en stabilitetsradiemodell som kännetecknas av ett enkelt stabilitetskrav av formen $r_{c}\leq R(q,u)$ där $q$ anger beslutet under övervägande, $u$ anger parametern av intresse, ${\tilde {u}}$ anger uppskattningen av det sanna värdet av $u$ och $U(\alpha ,{\tilde {u}})$ betecknar en boll med radien $\alpha$ centrerad på ${\tilde {u}}$ .

Eftersom stabilitetsradiemodeller är designade för att hantera små störningar i det nominella värdet av en parameter, mäter info-gaps robusthetsmodell den lokala robustheten för beslut i närheten av uppskattningen ${\tilde {u}}$ .

Sniedovich hävdar att teorin av denna anledning är olämplig för behandling av allvarlig osäkerhet som kännetecknas av en dålig uppskattning och ett stort osäkerhetsutrymme.

Alternativ definition

Det finns fall där det är bekvämare att definiera stabilitetsradien något annorlunda. Till exempel, i många tillämpningar inom kontrollteori definieras stabilitetsradien som storleken på den minsta destabiliserande störningen i det nominella värdet av parametern av intresse. Bilden är denna:

Mer formellt,

${\hat {\rho }}(q):=\min _{p\notin P(s) )}avstånd(p,{\hat {p}})$

där $dist(p,{\hat {p}})$ anger avståndet mellan $p\in P$ från ${\ hatt {p}}$ .

Stabilitetsradie för funktioner

Stabilitetsradien för en kontinuerlig funktion f (i ett funktionellt utrymme F ) med avseende på en öppen stabilitetsdomän D är avståndet mellan f och mängden instabila funktioner (med avseende på D ) . Vi säger att en funktion är stabil med avseende på D om dess spektrum är i D . Här definieras begreppet spektrum från fall till fall, som förklaras nedan.

Definition

Formellt, om vi betecknar mängden stabila funktioner med S(D) och stabilitetsradien med r(f,D) , då:

$r(f,D)=\inf _{g\in C}\{\|g \|:f+g\notin S(D)\},$

där C är en delmängd av F .

Observera att om f redan är instabil (med avseende på D ), så är r(f,D)=0 (så länge som C innehåller noll).

Ansökningar

Begreppet stabilitetsradie tillämpas generellt på speciella funktioner som polynom (spektrumet är då rötterna) och matriser (spektrumet är egenvärdena ) . Fallet där C är en riktig delmängd av F tillåter oss att överväga strukturerade störningar (t.ex. för en matris kan vi bara behöva störningar på den sista raden). Det är ett intressant mått på robusthet, till exempel inom kontrollteori .

Egenskaper

Låt f vara ett ( komplext ) polynom av grad n , C=F är mängden polynom med grad mindre än (eller lika med) n (som vi identifierar här med mängden $\mathbb {C} ^{n+1}$ av koefficienter). Vi tar för D den öppna enhetsskivan , vilket betyder att vi letar efter avståndet mellan ett polynom och mängden Schur- stabila polynom . Sedan:

$r(f,D)=\inf _{z\in \partial D}{\frac {|f(z)|}{\|q(z)\|}} ,$

där q innehåller varje basvektor (t.ex. $q(z)=(1,z,\ldots ,z^{n})$ när q är vanlig kraftbas). Detta resultat innebär att stabilitetsradien är bunden till det minimala värdet som f når på enhetscirkeln.

Exempel

• Polynomet $f(z)=z^{8}-9/10$ (vars nollor är 8:e rötterna av 0,9 ) har en stabilitetsradie på 1/80 om q är maktbasen och normen är oändlighetsnormen. Så det måste finnas ett polynom g med (oändlighets)norm 1/90 så att f+g har (minst) en rot på enhetscirkeln. Ett sådant g är till exempel $g(z)=-1/90\sum _{i=0}^{8}z^{i}$ . Faktum är att (f+g)(1)=0 och 1 är på enhetscirkeln, vilket betyder att f+g är instabilt.

Se även

• stabilt polynom
• Walds maximin-modell