Slagdjup
Islagsdjupet för en projektil är det avstånd den tränger in i ett mål innan den stannar. Fysikern Sir Isaac Newton utvecklade först denna idé för att få grova uppskattningar av islagsdjupet för projektiler som färdas med höga hastigheter.
Newtons approximation för islagsdjupet
Newtons approximation för islagsdjupet för projektiler vid höga hastigheter baseras endast på momentumöverväganden . Det sägs inget om vart stötkroppens rörelseenergi tar vägen, inte heller vad som händer med momentumet efter att projektilen stoppats.
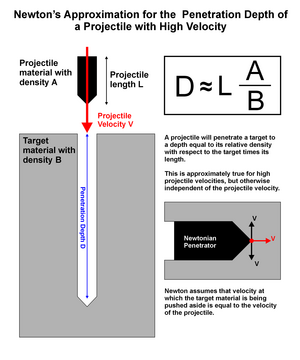
Grundidén är enkel: Impaktorn bär ett givet momentum. För att stoppa provkroppen måste detta momentum överföras till en annan massa. Eftersom stötkroppens hastighet är så hög att kohesionen inom målmaterialet kan försummas, kan rörelsemängden endast överföras till materialet (massan) direkt framför stötkroppen, som kommer att skjutas med stötkroppens hastighet. Om provkroppen har tryckt en massa som är lika med dess egen massa med denna hastighet, har hela dess rörelsemängd överförts till massan framför den och provkroppen kommer att stoppas. För en cylindrisk stötkropp, när den stannar, kommer den att ha penetrerat till ett djup som är lika med dess egen längd gånger dess relativa densitet med avseende på målmaterialet.
Detta tillvägagångssätt är endast giltigt för ett snävt område av hastigheter som är mindre än ljudets hastighet inom målet eller stötkroppsmaterialet.
Om anslagshastigheten är högre än ljudets hastighet inuti målet eller stötkroppsmaterialet, gör stötstöten att materialet spricker och vid högre hastigheter bete sig som en gas, vilket orsakar snabb utstötning av mål- och slagkroppsmaterial och bildandet av en krater . Djupet av kratern beror på materialegenskaperna hos stötkroppen och målet, såväl som islagshastigheten. Vanligtvis betyder högre anslagshastighet större kraterdjup.
Ansökningar
- Projektil : Helmetallprojektiler bör vara gjorda av ett material med mycket hög densitet, som uran (19,1 g/cm 3 ) eller bly (11,3 g/cm 3 ). Enligt Newtons uppskattning kommer en helmetallprojektil gjord av uran att tränga igenom ungefär 2,5 gånger sin egen längd av stålpansar.
- Formad laddning , bazooka : För att en formad laddning (antitank) ska tränga igenom stålplåtar är det viktigt att explosionen genererar en lång tungmetallstråle (i en formad laddning för pansarvärnsbruk genererar explosionen en höghastighetsmetall stråle från det konformade metallfodret). Denna jetstråle kan sedan ses som stötelementet för Newtons approximation.
- Meteorit : Som man kan dra slutsatsen av lufttrycket motsvarar atmosfärens material cirka 10 m vatten. Eftersom is har ungefär samma densitet som vatten måste en isbit från rymden som färdas med 15 km/s eller så ha en längd på 10 m för att nå jordens yta med hög hastighet. En mindre isbit kommer att bromsas till sluthastighet . En större isbit kan också bromsas, men så länge den kommer in i en mycket låg vinkel och därmed måste tränga igenom mycket atmosfär. En järnmeteorit med en längd av 1,3 m skulle slå genom atmosfären; en mindre skulle bromsas av luften och falla med sluthastighet till marken.
- Impactor, bunker buster : Solida stötdon kan användas istället för kärnstridsspetsar för att penetrera bunkrar djupt under jorden. Enligt Newtons uppskattning skulle en uranprojektil (densitet 19 g/cm 3 ) med hög hastighet och 1 m längd slå sig igenom 6 m sten (densitet 3 g/cm 3 ) innan den stannade.
Se även
Vidare läsning
- Young, CW (1967). Utvecklingen av empiriska ekvationer för att förutsäga djupet av en jordpenetrerande projektil ( Rapport). Vol. SC-DR-67-60. Albuquerque NM: Sandia National Laboratories.
-
Young, CW (1997). Penetration Equations (PDF) (Rapport). Vol. SAND94-2726. Albuquerque NM: Sandia National Laboratories.
Detta är en fristående rapport som dokumenterar den senaste uppdaterade versionen av Young/Sandias penetrationsekvationer och relaterade analytiska tekniker för att förutsäga penetration i naturliga jordmaterial och betong. Se Appendix A & B för introduktion till penetrationsekvationer.
- Alekseevskii, VP (1966). "Penetrering av en stav i ett mål med hög hastighet". Förbrännings-, explosions- och chockvågor (Fizika Goreniya i Vzryva) . 2 (2): 99–106. doi : 10.1007/BF00749237 . ISSN 0010-5082 . S2CID 97258659 .
- Tate, A. (1 november 1967). "En teori för inbromsningen av långa stavar efter stöten" ( PDF) . Journal of the Mechanics and Physics of Solids . 15 (6): 387–399. Bibcode : 1967JMPSo..15..387T . doi : 10.1016/0022-5096(67)90010-5 . Arkiverad från originalet (PDF) den 26 mars 2012 . Hämtad 23 juni 2011 .
- Bernard, Robert S. (1978). Förutsägelse av djup och rörelse för jordpenetratorer (Rapport). Vol. ADA056701. Vicksburg, MS: Army Engineer Waterways Experiment Station Vicksburg. Arkiverad från originalet (PDF) den 8 oktober 2012.
- Walters, William P.; Segletes, Steven B. (1991). "En exakt lösning av penetrationsekvationerna för långa stavar" . International Journal of Impact Engineering . 11 (2): 225–231. doi : 10.1016/0734-743X(91)90008-4 .
- Segletes, Steven B.; Walters, William P. (2002). Effektiv lösning av Long-Rod Penetration Equations of Alekseevskii-Tate ( PDF) (Rapport). Vol. ARL-TR-2855. Aberdeen, MD: Army Research Lab Aberdeen Proving Ground MD.
- Segletes, Steven B.; Walters, William P. (2003). "Utökningar till den exakta lösningen av ekvationerna för penetration/erosion med långa stavar" ( PDF) . International Journal of Impact Engineering . 28 (4): 363–376. doi : 10.1016/S0734-743X(02)00071-4 . Hämtad 23 juni 2011 .