Samlokalisering (fjärranalys)

Samlokalisering är en procedur som används vid fjärranalys för att matcha mätningar från två eller flera olika instrument. Detta görs av två huvudskäl: i valideringssyfte när man jämför mätningar av samma variabel, och för att relatera mätningar av två olika variabler antingen för att utföra hämtningar eller för att förutsäga. I det andra fallet matas data senare in i någon typ av statistisk invers metod , såsom ett artificiellt neuralt nätverk , statistisk klassificeringsalgoritm , kärnestimator eller en linjär minsta kvadrat . I princip kan de flesta samlokaliseringsproblem lösas genom att söka efter närmaste granne , men i praktiken finns det många andra överväganden inblandade och den bästa metoden är mycket specifik för den speciella matchningen av instrument. Här behandlar vi några av de viktigaste övervägandena tillsammans med specifika exempel.

Det finns åtminstone två huvudöverväganden när man utför samlokaliseringar. Det första är instrumentets samplingsmönster. Mätningar kan vara täta och regelbundna, såsom de från ett satellitinstrument som avsöker tvärspår. kan någon form av interpolation vara lämplig. Å andra sidan kan mätningarna vara sparsamma, till exempel en engångskampanj på fältet utformad för någon speciell valideringsövning. Det andra övervägandet är instrumentets fotavtryck, som kan sträcka sig från något som närmar sig en punktmätning som den för en radiosonde , eller den kan vara flera kilometer i diameter som den för en satellitmonterad mikrovågsradiometer. I det senare fallet är det lämpligt att ta hänsyn till instrumentantennmönstret när man gör jämförelser med ett annat instrument som har både ett mindre fotavtryck och en tätare sampling, det vill säga flera mätningar från det ena instrumentet kommer att passa in i det andras fotavtryck.

Precis som instrumentet har ett rumsligt fotavtryck kommer det också att ha ett tidsmässigt fotavtryck, ofta kallat integrationstiden. Även om integreringstiden vanligtvis är mindre än en sekund, vilket för meteorologiska tillämpningar i huvudsak är omedelbar, finns det många fall där någon form av tidsgenomsnitt avsevärt kan underlätta samlokaliseringsprocessen.

Samlokaliseringarna kommer att behöva screenas utifrån både tids- och längdskalorna för fenomenet av intresse. Detta kommer att underlätta samlokaliseringsprocessen ytterligare eftersom fjärranalys och andra mätdata nästan alltid lagras på något sätt. Vissa atmosfäriska fenomen som moln eller konvektion är ganska övergående så att vi inte behöver överväga kollokationer med ett tidsfel på mer än en timme eller så. Havsis, å andra sidan, rör sig och utvecklas ganska långsamt, så att mätningar åtskilda med så mycket som en dag eller mer fortfarande kan vara användbara.

Satelliter

Polar-stereografisk projektion som visar 12 timmars mätningar från tre AMSU-B-instrument

De satelliter som bekymrar oss mest är de med en låg polär omloppsbana eftersom geostationära satelliter ser samma punkt under hela sin livstid . Diagrammet visar mätningar från AMSU-B -instrument monterade på tre satelliter under en period av 12 timmar. Detta illustrerar både omloppsbanan och avsökningsmönstret som löper korsvis. Eftersom en satellits omloppsbana är deterministisk , utan omloppsmanövrar , kan vi förutsäga platsen för satelliten vid en given tidpunkt och, i förlängningen, platsen för mätpixlarna. I teorin kan samlokaliseringar utföras genom att invertera de bestämmande ekvationerna med början från den önskade tidsperioden. I praktiken innehåller partiellt bearbetade data (vanligtvis hänvisade till som nivå 1b, 1c eller nivå 2) koordinaterna för var och en av mätpixlarna och det är vanligt att helt enkelt mata dessa koordinater till en närmaste grannesökning. lagras satellitdata alltid på något sätt. Data kommer åtminstone att ordnas i strängar som sträcker sig från stolpe till stolpe. Spåren kommer att märkas efter tidsperiod och den ungefärliga platsen som är känd.

Radiosonder

Uppstigning av en väderballong som sjösatts från forskningsfartyget Polarstern

Radiosonder är särskilt viktiga för samlokaliseringsstudier eftersom de mäter atmosfäriska variabler mer exakt och mer direkt än satelliter eller andra fjärranalysinstrument. Dessutom är radiosondeprover i praktiken momentana punktmätningar. Ett problem med radiosonder som bärs upp av väderballonger är ballongdrift. I, detta hanteras genom att genomsnittet beräknas av alla satellitpixlar inom en radie på 50 km från ballonguppskjutningen.

Histogram över uppstigningshastigheter för väderballonger som lanseras från forskningsfartyget Polarstern

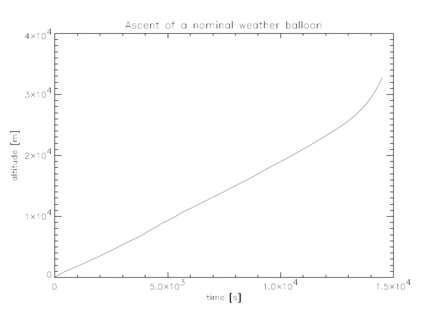
Om högupplösta sonddata, som normalt har en konstant samplingshastighet eller inkluderar mättiden, används, kan sidorörelsen spåras från vinddata. Även med lågupplösta data kan rörelsen fortfarande approximeras genom att anta en konstant uppstigningshastighet. Förutom en kort bit mot slutet kan den linjära stigningen tydligt ses i figuren ovan. Vi kan visa att uppstigningshastigheten för en ballong ges av följande ekvation

$v={\sqrt {\frac {gkh(1-R_{a}/R_{s})}{c_{D}}} }$

där g är gravitationsacceleration, k relaterar ballongens höjd, h och ytarea, A , till dess volym: V = khA ; R _s är ballongens ekvivalenta "gaskonstant", _Ra är luftens gaskonstant och c _D är luftmotståndskoefficienten för ballongen. Genom att ersätta några förnuftiga värden för var och en av konstanterna, k =1. (ballongen är en perfekt cylinder), h =2. m, c _D = 1. och Ra är gaskonstanten för helium, ger en uppstigningshastighet på 4,1 m/s _. Jämför detta med värdena som visas i histogrammet som sammanställer alla radiosondeuppskjutningar från forskningsfartyget Polarstern under en period av elva år mellan 1992 och 2003.

Interpolation

För rutnätsdata som assimilerings- eller omanalysdata är interpolering troligen den lämpligaste metoden för att utföra någon typ av jämförelse . En specifik punkt i både fysisk position och tid är lätt att lokalisera inom nätet och interpolation utförs mellan de närmaste grannarna. Linjär interpolation ( bilinjär , trilinjär etc.) är den vanligaste, även om kubisk används också men är förmodligen inte värt den extra beräkningskostnaden. Om variabeln av intresse har en relativt jämn förändringshastighet (temperatur är ett bra exempel på detta eftersom den har en diffusionsmekanism, strålningsöverföring , som inte är tillgänglig för andra atmosfäriska variabler), då kan interpolation eliminera mycket av felet i samband med samlokalisering.

Interpolation kan också vara lämpligt för många typer av satellitinstrument, till exempel ett cross-track scanning instrument som Landsat . I data som härrör från Advanced Microwave Sounding Unit ( AMSU) interpoleras (även om det inte är för samlokaliseringsändamål) med en liten variation av trilinjär interpolation. Eftersom mätningar inom ett enda avsökningsspår läggs ut i ett ungefärligen rektangulärt rutnät, kan bilinjär interpolation utföras. Genom att söka efter det närmaste överlappande avsökningsspåret både framåt och bakåt i tiden, kan de rumsliga interpoleringarna sedan interpoleras i tiden. Denna teknik fungerar bättre med härledda kvantiteter snarare än obearbetade ljusstyrketemperaturer eftersom skanningsvinkeln redan har tagits med i beräkningen.

För instrument med ett mer oregelbundet samplingsmönster, såsom Advanced Microwave Scanning Radiometer-EOS (AMSR-E) instrumentet som har ett cirkulärt avsökningsmönster, behöver vi en mer generell form av interpolation, såsom kärnuppskattning . En metod som vanligtvis används för just detta instrument, såväl som SSM/I , är ett enkelt dagligt medelvärde inom regelbundet rutnät, rumsliga fack.

Banor

För att samlokalisera mätningar av ett medel- till långlivat atmosfäriskt spårämne med ett andra instrument, kan löpande banor förbättra noggrannheten avsevärt. Det förenklar också analysen något: en bana körs både framåt och bakåt från mätplatsen och mellan önskat tidsfönster. Observera att det acceptabla tidsfönstret nu har blivit längre eftersom felet från transportinducerade förändringar i spårämnet har tagits bort: spårämnets livslängd skulle vara ett bra fönster att använda. Eftersom banorna tillhandahåller en plats för varje tidpunkt inom tidsfönstret, finns det inget behov av att kontrollera flera mätningar från det andra instrumentet. Varje gång inom banan kontrolleras för avståndskriteriet men inom ett mycket smalt fönster. Alternativt interpoleras de exakta tiderna för mätningarna för det andra instrumentet inom banan. Endast det minsta avståndsfelet under tröskeln används och avståndskriteriet kan göras mindre som en konsekvens.

Exempel: Pol-Is-kampanj

Karta över EM Bird-flyg från Pol-Ice-kampanjen tillsammans med sammanfallande EMIRAD-flyg

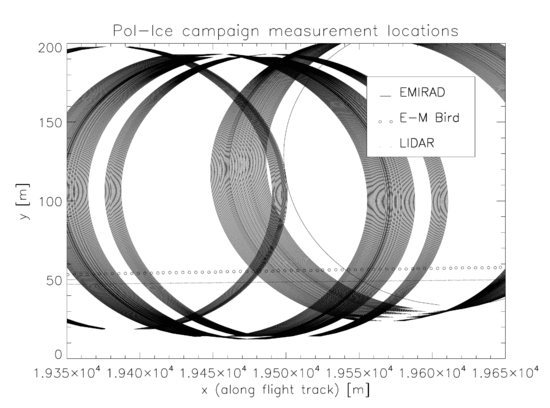
Samlokaliseringar av havsisens tjocklek och ljushetstemperaturer tagna under Pol-Is-kampanjen är ett utmärkt exempel eftersom de illustrerar många av de viktigaste principerna samt visar på nödvändigheten av att ta hänsyn till det enskilda fallet. Pol-Ice-kampanjen genomfördes i N. Baltikum i mars 2007 som en del av SMOS-Ice-projektet som förberedelse för uppskjutningen av satelliten Soil Moisture and Ocean Salinity . På grund av den låga frekvensen av SMOS-instrumentet hoppas man att det ska ge information om havsisens tjocklek, därför omfattade kampanjen mätningar av både havsisens tjocklek och den utsända ljusstyrkan. Ljusstyrka temperaturer mättes med EMIRAD L-band mikrovågsradiometer som bars ombord på ett flygplan. Istjockleken mättes med istjockleksmätaren EM Bird som bars av en helikopter. EM Bird mäter istjockleken med en kombination av induktansmätningar för att bestämma platsen för is-vattengränssnittet och en laserhöjdmätare för att mäta höjden på isytan. Kartan ovan visar flygspåren för båda instrumenten som var ungefär sammanfallande men uppenbarligen föremål för pilotfel.

EMIRAD antennsvarsmönster

Eftersom flygvägarna för båda flygplanen var ungefär linjära, var det första steget i samlokaliseringsprocessen att konvertera alla sammanfallande flygningar till kartesiska koordinater med x-axeln som sidoavstånd och y - axelns tväravstånd. På detta sätt kan samlokaliseringar utföras på två sätt: grovt, genom att endast matcha x- avstånden, och mer exakt genom att matcha båda koordinaterna.

Ännu viktigare är att radiometerns fotavtrycksstorlek är många gånger större än EM Bird-mätarens. Bilden till vänster visar antennsvarsfunktionen för radiometern. Hela bredden vid halva max är 31 grader. Eftersom flygplanet flög på cirka 500 m, översätts detta till en fotavtrycksstorlek på 200 m eller mer. Samtidigt var EM-fågelns fotavtryck ungefär 40 m med ett provavstånd på endast 2 till 4 m. Istället för att titta till närmaste grannar, vilket skulle ha gett dåliga resultat, utfördes ett viktat medelvärde av tjockleksmätningarna för varje radiometermätning. Vikter beräknades utifrån radiometerns svarsfunktion som är nästan en perfekt Gauss upp till cirka 45 grader. Poäng kan uteslutas baserat på avstånd längs flygvägen. För validering av beräkningar av havsis-emissivitet framåt modell, förfinades detta ytterligare genom att utföra en emissivitetsberäkning för varje tjockleksmätning och ett medelvärde över radiometerns fotavtryck.

Figuren nedan illustrerar relativa mätplatser från vart och ett av instrumenten som används i Pol-Is-kampanjen. Två överfarter visas: en från flygplanet som bär EMIRAD-radiometern och en från helikoptern som bär EM Bird-instrumentet. X-axeln är längs linjen för flygbanan. EMIRADs fotspår ritas med linjer, EM Bird-induktansmätningar representeras av cirklar och LIDAR-mått med prickar.

Relativa mätplatser från P4X till P2A flygspår: se ovan karta. EMIRADs fotspår representerar den Gaussiska standardavvikelsen, inte FWHM.