Kärna (statistik)

För annan användning, se Kernel (disambiguation) .

Termen kärna används i statistisk analys för att referera till en fönsterfunktion . Termen "kärna" har flera distinkta betydelser i olika grenar av statistik.

Bayesiansk statistik

I statistik, särskilt i Bayesiansk statistik , är kärnan i en sannolikhetstäthetsfunktion (pdf) eller sannolikhetsmassfunktion (pmf) formen av pdf eller pmf där alla faktorer som inte är funktioner för någon av variablerna i domänen är utelämnad. Observera att sådana faktorer mycket väl kan vara funktioner av parametrarna för pdf eller pmf. Dessa faktorer utgör en del av normaliseringsfaktorn för sannolikhetsfördelningen och är onödiga i många situationer. Till exempel, vid pseudo-slumptalssampling ignorerar de flesta samplingsalgoritmer normaliseringsfaktorn. Dessutom, i Bayesiansk analys av konjugerade tidigare fördelningar, ignoreras normaliseringsfaktorerna i allmänhet under beräkningarna, och endast kärnan beaktas. I slutet undersöks kärnans form, och om den matchar en känd fördelning kan normaliseringsfaktorn återställas. Annars kan det vara onödigt (till exempel om distributionen bara behöver tas ur).

För många distributioner kan kärnan skrivas i sluten form, men inte normaliseringskonstanten.

Ett exempel är normalfördelningen . Dess sannolikhetstäthetsfunktion är

$p(x|\mu ,\sigma ^{2})={\frac {1} {\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}$

och den associerade kärnan är

$p(x|\mu ,\sigma ^{2})\propto e^{-{\frac {(x -\mu )^{2}}{2\sigma ^{2}}}}$

Observera att faktorn framför exponentialen har utelämnats, även om den innehåller parametern ${\displaystyle \sigma ^{2}} ,$ eftersom den inte är en funktion av domänvariabeln $x$ .

Mönsteranalys

Kärnan i en reproducerande kärna Hilbert-utrymme används i den svit av tekniker som kallas kärnmetoder för att utföra uppgifter som statistisk klassificering , regressionsanalys och klusteranalys av data i ett implicit utrymme. Denna användning är särskilt vanlig inom maskininlärning .

Icke-parametrisk statistik

Ytterligare information: Kärnutjämning

I icke-parametrisk statistik är en kärna en viktningsfunktion som används i icke-parametriska uppskattningstekniker. Kärnor används vid uppskattning av kärndensitet för att uppskatta slumpvariablernas densitetsfunktioner , eller i kärnregression för att uppskatta den villkorade förväntan av en slumpvariabel . Kärnor används också i tidsserier , i användningen av periodogrammet för att uppskatta den spektrala tätheten där de är kända som fönsterfunktioner . En ytterligare användning är uppskattningen av en tidsvarierande intensitet för en punktprocess där fönsterfunktioner (kärnor) konvolveras med tidsseriedata.

Vanligtvis måste kärnbredder också anges när en icke-parametrisk uppskattning körs.

Definition

Ytterligare information: Integral kärna

En kärna är en icke-negativ realvärd integrerbar funktion K. För de flesta applikationer är det önskvärt att definiera funktionen för att uppfylla två ytterligare krav:

• Normalisering :

$\int _{-\infty }^{+\infty }K(u)\,du=1\,;$

• Symmetri:

$K(-u)=K(u){\mbox{ för alla värden på }}u\,.$

Det första kravet säkerställer att metoden för kärndensitetsuppskattning resulterar i en sannolikhetstäthetsfunktion . Det andra kravet säkerställer att medelvärdet av motsvarande fördelning är lika med det för det använda urvalet.

Om K är en kärna, så är funktionen K * definierad av K *( u ) = λ K (λ u ), där λ > 0. Detta kan användas för att välja en skala som är lämplig för data.

Kärnfunktioner i vanligt bruk

Alla kärnor nedan i ett gemensamt koordinatsystem.

Flera typer av kärnfunktioner används vanligtvis: enhetlig, triangel, Epanechnikov, quartic (biweight), tricube, triweight, Gaussian, kvadratisk och cosinus.

I tabellen nedan, om $K$ ges med ett begränsat stöd , då $K(u)=0$ för värden på u som ligger utanför stödet.

Kärnfunktioner, K ( u )			$\textstyle \int u^{2}K(u)du$	$\textstyle \int K(u)^{2}du$	Effektivitet i förhållande till Epanechnikov-kärnan
Uniform ("rektangulärt fönster")	$K(u)={\frac {1}{2}}$ Support: $|u|\leq 1$	" Lådbilsfunktion "	${\frac {1}{3}}$	${\frac {1}{2}}$	92,9 %
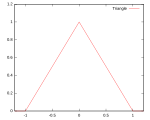
Triangulär	$K(u)=(1-|u|)$ Support: $|u|\leq 1$		${\frac {1}{6}}$	${\frac {2}{3}}$	98,6 %
Epanechnikov (parabolisk)	$K(u)={\frac {3}{4}}(1-u^{2})$ Support: $|u|\leq 1$		${\frac {1}{5}}$	${\frac {3}{5}}$	100 %
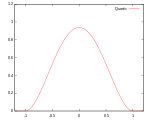
Quartic (bivikt)	$K(u)={\frac {15}{16}}(1-u^{2})^{2}$ Support: $|u|\leq 1$		${\frac {1}{7}}$	${\frac {5}{7}}$	99,4 %
Trevikt	$K(u)={\frac {35}{32}}(1-u^{2})^{3}$ Support: $|u|\leq 1$		${\frac {1}{9}}$	${\frac {350}{429}}$	98,7 %
Tricube	$K(u)={\frac {70}{81}}(1-{\left|u\right|}^{3} )^{3}$ Support: $|u|\leq 1$		${\frac {35}{243}}$	${\frac {175}{247}}$	99,8 %
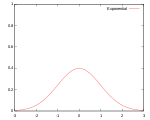
Gaussisk	$K(u)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2 }}u^{2}}$		$1\,$	${\frac {1}{2{\sqrt {\pi }}}}$	95,1 %
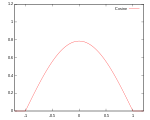
Cosinus	$K(u)={\frac {\pi }{4}}\cos \left({\frac {\pi }{2}}u \höger)$ Support: $|u|\leq 1$		$1-{\frac {8}{\pi ^{2}}}$	${\frac {\pi ^{2}}{16}}$	99,9 %
Logistisk	$K(u)={\frac {1}{e^{u}+2+e^{-u}}}$		${\frac {\pi ^{2}}{3}}$	${\frac {1}{6}}$	88,7 %
Sigmoid funktion	$K(u)={\frac {2}{\pi }}{\frac {1}{e^{u}+e^{- u}}}$		${\frac {\pi ^{2}}{4}}$	${\frac {2}{\pi ^{2}}}$	84,3 %
Silverman kärna	$K(u)={\frac {1}{2}}e^{-{\frac {|u|}{\sqrt {2}} }}\cdot \sin \left({\frac {|u|}{\sqrt {2}}}+{\frac {\pi }{4}}\right)$		$0$	${\frac {3{\sqrt {2}}}{16}}$	inte tillämpbar

Se även

• Uppskattning av kärndensitet
• Kärnan mjukare
• Stokastisk kärna
• Positivt-definierad kärna
• Densitetsuppskattning
• Multivariat kärndensitetsuppskattning

•   Li, Qi; Racine, Jeffrey S. (2007). Ickeparametrisk ekonometri: teori och praktik . Princeton University Press. ISBN 978-0-691-12161-1 .

• Zucchini, Walter. "TILLÄMPAD UTLÄTTNINGSTEKNIK Del 1: Uppskattning av kärndensitet" (PDF) . Hämtad 6 september 2018 .

•   Comaniciu, D; Meer, P (2002). "Mean shift: A robust approach to feature space analysis". IEEE-transaktioner på mönsteranalys och maskinintelligens . 24 (5): 603–619. CiteSeerX 10.1.1.76.8968 . doi : 10.1109/34.1000236 .