Pyknon

Pyknon (från grekiska : πυκνόν ), ibland också translittererad som pycnon (från grekiska : πυκνός tätt, tätt packat, trångt, förtätat; latin : spissus ) i antikens musikteori är en strukturell egenskap hos vilken som helst tetrachord två mindre intervall är mindre än det återstående ( inkomposita ) intervallet. Pyknonens sammansättning tjänar till att identifiera det melodiska släktet (även kallat "släktet av en tetrachord") och oktavarten som skapas genom att sammansätta två sådana tetrachords, och reglerna som styr sätten på vilka sådana föreningar kan göras fokuserar på relationerna mellan de två inblandade pykna .

Definition

Pyknonen var ett viktigt kriterium vid klassificeringen av melodiska släkten ( grekiska : γένη τῶν μελῳδουμένων ) . Det grekiska ordet πυκνόν är ett adjektiv som betyder "nära", "kompakt", "trängt" eller "trångt". I forntida grekisk musikteori används denna term för att beskriva ett par intervall inom ett tetrachord , vars summa är mindre än resten av tetrachordet. Även om ett tetrachord i modernt bruk kan vara vilket fyratoners segment av en skala som helst , eller faktiskt vilken (oordnad) samling av fyra tonhöjdsklasser som helst, i antik grekisk musikteori består ett tetrachord av ett fyratonssegment av det större och mindre perfekta System som begränsas av intervallet för en perfekt fjärdedel, vars yttre toner förblir fixerade i alla släkten och därför kallas "stående toner" ( grekiska : ἑστῶτες φθόγγοι ). Placeringen av de inre noterna varierar från ett släkte till ett annat, varför de kallas "rörliga noter". I sin grundläggande teoretiska form är det största intervallet för ett tetrachord överst och det minsta längst ner. Förekomsten av en pyknon beror därför på att det översta intervallet är större än hälften av en perfekt fjärdedel, vilket bara förekommer i de kromatiska och enharmoniska släktena . Eftersom det diatoniska släktet består av två heltoner och en halvton, är inget enskilt intervall större än de andra två kombinerat, och det finns alltså ingen pyknon . Av denna anledning kallas de enharmoniska och kromatiska släktena ibland för "pykniska släkten", för att skilja dem från de diatoniska.

Teoretiska tillämpningar

Anteckningarna av den centrala tetrachorden av systemet i stigande ordning är hypate , parhypate , lichanos (eller hypermese ) och mese . Ett andra tetrachord läggs till ovan, efter en disjunktiv ton, och motsvarande namn (tillsammans med intervallförhållandena för de stående tonerna) är:

• mese (4:3) – nete (2:1) (stående)
• lichanos – paranete (rörlig)
• parhypate – banalt (rörlig)
• hypate (1:1) – paramese (3:2) (stående)

Även om den är rörlig, måste lichanos förbli ovanför parhypaten och paraneten ovanför triteen .

Ett "sammansatt intervall" är ett som består av två eller flera mindre intervall; ett "inkompositintervall" har inga mindre komponenter. I dessa termer, om det sammansatta intervallet mellan hypaten och lichanos (eller paramese och paranete ) är mindre än det inkomposita intervallet från lichanos till mese (eller paranete till nete ), de tre toner i det sammansatta intervallet kallas tillsammans en pyknon . I det diatoniska släktet, eftersom det sammansatta intervallet från hypat till lichanos (en mindre tredjedel) är större än det återstående inkomposita intervallet från lichanos till mese (en hel ton), betecknas de tre lägsta tonerna i det diatoniska tetrachordet apyknon : "inte nära -packade".

Enharmonisk

Två pykniska enharmoniska tetrachord som tillsammans utgör den grekiska doriska oktavarten i det enharmoniska släktet

I det enharmoniska släktet var det stora inkomposita intervallet ursprungligen en ditone (den stora tredjedelen av Pythagoras stämning ), vilket lämnade en pyknon med en total bredd på bara en halvton . Den pythagoreiska ditonen motsvarar två 9:8 epogdoa , eller större sekunder ), tillsammans ett intervall på 81:64, vilket lämnar en pyknon på 256:243 – en limma (mindre pythagoreisk halvton), men exakt hur pyknon var (det är genom exakt matematisk beräkning) uppdelad i dess två komponentintervall är inte känt. Stämningen av Eratosthenes , som rapporterats av Aristoxenus , använder en stor tredjedel av 19:15 med de två ojämna intervallen för pyknonen i förhållandena 40:39 och 39:38. Även om Aristoxenus också antyder att de två intervallen för pyknonen i det enharmoniska släktet kan vara lika, är den anonyma författaren till Euclidian Sectio Canonis (P18) otvetydig: " Parhypatai och tritai delar inte upp pyknon i lika intervall".

Ptolemaios rapporterar i sin Harmonics (2.14) att två andra teoretiker, Archytas och Didymus , ersatte ditonen med den mindre, bara stora tredjedelen med talförhållandet 5:4, vilket gjorde pyknonen i motsvarande grad större. Denna pyknon delades olika upp av dessa två teoretiker, men i båda fallen var de två intervallen inte lika med varandra. Archytas, som var den första teoretikern som gav förhållanden för alla släktena, valde 28:27 och 36:35, och Didymus, cirka fyra århundraden senare, gav 32:31 och 31:30.

Kromatisk

Två pykniska kromatiska tetrachords, tillsammans bestående av den grekiska doriska oktavarten i det kromatiska släktet

I det kromatiska släktet kallades det största intervallet för en grekisk : τριημιτόνιόν ἀσύνθετον , latin : triemitonium incompositum —översatt som "inkomposit" (eller "icke-sammansatt" (eller "icke-sammansatt" (eller "icke-sammansatt") (föredrar en översättning, bar, bar och skrift) " ett individuellt intervall på tre halvtoner"; Strunk använder "trisemitoner"), den moderna termen är " minor terts " - vilket lämnar en pyknon av någon typ av helton som ska delas upp i två halvtoner. Det finns ett större antal variationer i stämningen av den kromatiska än i den enharmoniska. Fram till början av 300-talet f.Kr. spänner den kromatiska pyknonen över en stor helton med förhållandet 9:8, och denna delades upp av Gaudentius i stigande halvtonsintervall på 256:243 och 2187:2048. Ptolemaios definierade två olika stämningar av det kromatiska släktet: den "mjuka" kromatiska med en mindre pyknon och den "intensiva" kromatiska med en större. De ojämna halvtonerna som delar pykna var i förhållandet 28:27 och 15:14 för den mjuka kromatiska och 22:21 och 12:11 för den intensiva. Det större återstående intervallet var 6:5 i den mjuka kromatiska och 7:6 i den intensiva.

Skalstruktur

Grekiska mixolydiska oktavarter på E i det kromatiska släktet: konjunkta tetrachords a och b , med ton av konjunktion c , och intervall för disjunktion d ; de två pykna är åtskilda av det större intervallet mellan steg 3 och 4   Spela

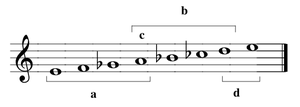
En ytterligare förfining av tetrachordal konstruktion, enligt Aristoxenus , är att det nedre intervallet av pyknon måste vara mindre än eller lika med det övre. Didymus i det kromatiska släktet och Archytas i det enharmoniska bröt dock denna regel, och i Harmonics (2. 13) kritiserade Ptolemaios detta drag hos Didymus och menade att det är omelodiskt och inte överensstämmer med våra örons bevis.

Enligt Aristoxenus Elementa harmonica ( Elements of Harmony , bok 2), närhelst tetrachord kombineras för att bilda en skala som fyller en oktav, "två på varandra följande pycna kanske inte förekommer i uppstigning eller nedstigning. En diton kan föregå eller följa [en pycnon] i stigning eller nedstigning. En ton kan följa [en pycnon] endast i nedstigning".

•   Barbera, André (1977). "Aritmetiska och geometriska divisioner av Tetracordet". Tidskrift för musikteori . 21 (2 - Höst): 294–323. doi : 10.2307/843492 . JSTOR 843492 .
•   Barbera, André (1984). "Oktav arter". Tidskriften för musikvetenskap . 3 (3 - Sommar): 229–241. doi : 10.2307/763813 . JSTOR 763813 .
•    Barker, Andrew (1981). "Metoder och mål i den euklidiska Sectio Canonis". Journal of Hellenic Studies . 101 : 1–16. doi : 10.2307/629840 . JSTOR 629840 . S2CID 162356270 .
•   Chalmers, John (1990). Larry Polansky; Carter Scholz (red.). Divisioner av Tetracordet . Libanon NH: Frog Peak Music. ISBN 0-945996-04-7 .
•   Levin, Flora R. (2007). "Ἀπειρία i Aristoxenian Theory". Hermes . 135 (4): 406–428. doi : 10.25162/hermes-2007-0038 . S2CID 151484983 .
•   Mathiesen, Thomas J. (1999). Apollos Lyra: Grekisk musik och musikteori i antiken och medeltiden . Lincoln : University of Nebraska Press. ISBN 9780803230798 .
•   Solomon, Jon (1984). "Mot en historia av Tonoi". Tidskriften för musikvetenskap . 3 (3 - Sommar): 242–251. doi : 10.2307/763814 . JSTOR 763814 .

Fotnoter

Vidare läsning

• Mathiesen Thomas J. 2001. "Greece, §I: Ancient", The New Grove Dictionary of Music and Musicians, andra upplagan, redigerad av Stanley Sadie och John Tyrrell. London: Macmillan Publishers.
• Winnington-Ingram, Reginald Pepys. 1936. Mode i antik grekisk musik . Cambridge Classical Studies 2. Cambridge: The University Press. Omtryckt, Chicago, Argonaut Inc., 1967; Amsterdam: Adolf M. Hakkert, 1968.