Prandtl–Meyer expansionsfläkt
En överljudsexpansionsfläkt, tekniskt känd som Prandtl–Meyer expansionsfläkt, en tvådimensionell enkel våg , är en centrerad expansionsprocess som uppstår när ett överljudsflöde vänder sig runt ett konvext hörn. Fläkten består av ett oändligt antal Mach-vågor , som divergerar från ett skarpt hörn. När ett flöde vänder sig runt ett jämnt och cirkulärt hörn kan dessa vågor förlängas bakåt för att mötas vid en punkt.
Varje våg i expansionsfläkten vänder flödet gradvis (i små steg). Det är fysiskt omöjligt för flödet att svänga genom en enda "chock"våg eftersom detta skulle bryta mot termodynamikens andra lag .
Över expansionsfläkten accelererar flödet (hastigheten ökar) och Mach-talet ökar, medan det statiska trycket , temperaturen och densiteten minskar. Eftersom processen är isentropisk förblir stagnationsegenskaperna (t.ex. det totala trycket och den totala temperaturen ) konstanta över fläkten.
Teorin beskrevs av Theodor Meyer på sin avhandling 1908, tillsammans med sin rådgivare Ludwig Prandtl , som redan hade diskuterat problemet ett år tidigare.
Flödesegenskaper
Expansionsfläkten består av ett oändligt antal expansionsvågor eller Mach-linjer . Den första Mach-linjen har en vinkel med avseende på flödesriktningen, och den sista Mach-linjen har en vinkel med avseende på slutlig flödesriktning. Eftersom flödet vänder i små vinklar och förändringarna över varje expansionsvåg är små, är hela processen isentropisk. Detta förenklar beräkningarna av flödesegenskaperna avsevärt. Eftersom flödet är isentropiskt, stagnationsegenskaper som stagnationstryck ( ), stagnationstemperatur ( ) och stagnationstäthet ( ) förbli konstant. De slutliga statiska egenskaperna är en funktion av det slutliga flödet Mach-tal ( ) och kan relateras till de initiala flödesförhållandena enligt följande, där är värmekapacitetsförhållandet av gasen (1,4 för luft):
Mach-talet efter svängen ( ) är relaterat till det initiala Mach-numret ( ) och svängvinkeln ( ) förbi,
där är Prandtl–Meyer-funktionen . Denna funktion bestämmer vinkeln genom vilken ett ljudflöde ( M = 1) måste vända för att nå ett visst Mach-tal (M). Matematiskt,
Enligt konventionen är
Sålunda, givet det initiala Mach-talet ( ), kan man beräkna och använda vridningsvinkeln hitta . Från värdet på kan man få det slutliga Mach-talet ( och de andra flödesegenskaperna. Hastighetsfältet i expansionsfläkten, uttryckt i polära koordinater ges av
är den specifika entalpin och är den stagnationsspecifika entalpin.
Maximal svängvinkel
Eftersom Mach-talet varierar från 1 till , tar värden från 0 till där
Detta sätter en gräns för hur mycket ett överljudsflöde kan svänga igenom, med den maximala svängvinkeln som ges av,
Man kan också se på det så här. Ett flöde måste vända så att det kan uppfylla randvillkoren. I ett idealt flöde finns det två typer av gränsvillkor som flödet måste uppfylla,
- Hastighetsgränsvillkor, som dikterar att komponenten av flödeshastigheten vinkelrät mot väggen är noll. Det är också känt som no-penetration boundary condition.
- Tryckgränsvillkor, som säger att det inte kan finnas en diskontinuitet i det statiska trycket inuti flödet (eftersom det inte finns några stötar i flödet).
Om flödet vänder tillräckligt så att det blir parallellt med väggen behöver vi inte oroa oss för tryckgränsvillkor. Men när flödet vänder, minskar dess statiska tryck (som beskrivits tidigare). Om det inte finns tillräckligt med tryck för att börja med kommer flödet inte att kunna slutföra svängen och kommer inte att vara parallellt med väggen. Detta visas som den maximala vinkeln genom vilken ett flöde kan vända. Ju lägre Mach-talet är att börja med (dvs. liten ), desto större är den maximala vinkeln genom vilken flödet kan vända.
Strömlinjen som skiljer den slutliga flödesriktningen och väggen är känd som en slipström (visas som den streckade linjen i figuren). Över denna linje finns ett hopp i hastighetens temperatur, densitet och tangentiella komponent (normal komponent är noll). Bortom slipströmmen är flödet stillastående (vilket automatiskt uppfyller hastighetsgränsvillkoret vid väggen). Vid verkligt flöde observeras ett skjuvskikt istället för en slipström, på grund av det ytterligare halkfria gränsvillkoret .
Anteckningar
-
^ a b
Omöjlighet att expandera ett flöde genom en enda "chock"-våg: Betrakta scenariot som visas i den intilliggande figuren. När ett överljudsflöde vänder ökar hastighetens normala komponent ( ), medan den tangentiella komponenten förblir konstant ( ). Motsvarande förändring är entropin ( ) kan uttryckas enligt följande,
där är den universella gaskonstanten, är förhållandet mellan specifika värmekapaciteter, är den statiska densiteten, är den statiska tryck, är entropin och är komponenten av flödeshastighet som är normal mot "chocken". Suffixet "1" och "2" hänvisar till de initiala respektive slutliga förhållandena.
Eftersom skulle detta betyda att . Eftersom detta inte är möjligt betyder det att det är omöjligt att vända ett flöde genom en enda stötvåg. Argumentet kan utökas ytterligare för att visa att en sådan expansionsprocess endast kan ske om vi betraktar en sväng genom ett oändligt antal expansionsvågor i gränsen . Följaktligen är en expansionsprocess en isentropisk process .
- ^ Meyer, T. (1908). Über zweidimensionale Bewegungsvorgänge in einem Gas, das mit Überschallgeschwindigkeit strömt ( Doktorsavhandling) (på tyska). Georg-August Universität, Göttingen. OCLC 77709738 .
- ^ Prandtl, L. (1907). "Neue Untersuchungen über die strömende Bewegung der Gase und Dämpfe". Physikalische Zeitschrift (på tyska). 8 :23–30. Omtryckt i Riegels, FW, ed. (1961). Ludwig Prandtl Gesammelte Abhandlungen . Berlin: Springer. doi : 10.1007/978-3-662-11836-8_78 .
-
^
Mach-linjer (kon) och Mach-vinkel:
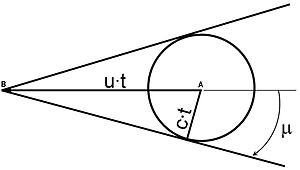 För ett föremål som rör sig med överljudshastigheter ( ) när det rör sig från punkt A till B (avstånd u·t), färdas störningarna som härrör från punkt A ett avstånd c·t. Motsvarande vinkel är känd som en Mach-vinkel och linjerna som omsluter det störda området är kända som Mach-linjer (i 2-D-fall) eller Mach-kon (i 3-D).
För ett föremål som rör sig med överljudshastigheter ( ) när det rör sig från punkt A till B (avstånd u·t), färdas störningarna som härrör från punkt A ett avstånd c·t. Motsvarande vinkel är känd som en Mach-vinkel och linjerna som omsluter det störda området är kända som Mach-linjer (i 2-D-fall) eller Mach-kon (i 3-D).Mach-linjer är ett begrepp som vanligtvis påträffas i 2D-överljudsflöden (dvs. . De är ett par avgränsande linjer som skiljer området med stört flöde från den ostörda delen av flödet. Dessa linjer förekommer i par och är orienterade i en vinkel
med avseende på rörelseriktningen (även känd som Mach-vinkeln ). Vid 3D-flödesfält bildar dessa linjer en yta som kallas Mach-kon , med Mach-vinkel som konens halva vinkel.
För att förstå konceptet bättre, överväg fallet som skisseras i figuren. Vi vet att när ett föremål rör sig i ett flöde, orsakar det tryckstörningar (som färdas med ljudets hastighet, även kända som Mach-vågor ). Figuren visar ett föremål som rör sig från punkt A till B längs linjen AB med överljudshastigheter ( . När objektet når punkt B har tryckstörningarna från punkt A tillryggalagt ett avstånd c·t och befinner sig nu vid cirkelns omkrets (med centrum i punkt A). Det finns oändliga sådana cirklar med centrum på linjen AB, var och en representerar platsen för störningarna på grund av objektets rörelse. Linjerna som fortplantar sig utåt från punkt B och tangerar alla dessa cirklar är kända som Mach-linjer.
Notera: Dessa begrepp har en fysisk betydelse endast för överljudsflöden ( . Vid subsoniska flöden kommer störningarna att färdas snabbare än källan och argumentet för kommer att vara större än en.
- ^ Landau, LD, & Lifshitz, EM (2013). Fluid Mechanics: Landau och Lifshitz: Kurs i teoretisk fysik, Volym 6 (Vol. 6). Elsevier.
Se även
- Liepmann, Hans W.; Roshko, A. (2001) [1957]. Element av gasdynamik . Dover Publikationer . ISBN 0-486-41963-0 .
- Von Mises, Richard (2004) [1958]. Matematisk teori för komprimerbart vätskeflöde . Dover Publikationer . ISBN 0-486-43941-0 .
- Courant, Richard; Friedrichs, KO (1999) [1948]. Överljudsflöde och stötvågor . Springer Science+Business Media . ISBN 0387902325 .
- Anderson, John D. Jr. (januari 2001) [1984]. Fundamentals of Aerodynamics (3:e upplagan). McGraw-Hill vetenskap/teknik/matematik . ISBN 0-07-237335-0 .
- Shapiro, Ascher H. (1953). Dynamiken och termodynamiken för komprimerbart vätskeflöde, volym 1 . Ronald Press. ISBN 978-0-471-06691-0 .








![{\displaystyle {\begin{aligned}{\frac {T_{2}}{T_{1}}}&=\left({\frac {1+{\frac {\gamma -1}{2}}M_{1}^{2}}{1+{\frac {\gamma -1}{2}}M_{2}^{2}}}\right)\\[3pt]{\frac {p_{2}}{p_{1}}}&=\left({\frac {1+{\frac {\gamma -1}{2}}M_{1}^{2}}{1+{\frac {\gamma -1}{2}}M_{2}^{2}}}\right)^{\frac {\gamma }{\gamma -1}}\\[3pt]{\frac {\rho _{2}}{\rho _{1}}}&=\left({\frac {1+{\frac {\gamma -1}{2}}M_{1}^{2}}{1+{\frac {\gamma -1}{2}}M_{2}^{2}}}\right)^{\frac {1}{\gamma -1}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d7fb657f76f99c2c63055d54ea500510133296d)























![{\displaystyle {\begin{aligned}{\frac {\Delta s}{R}}&=\ln \left[\left({\frac {p_{2}}{p_{1}}}\right)^{\frac {1}{\gamma -1}}\left({\frac {\rho _{2}}{\rho _{1}}}\right)^{-{\frac {\gamma }{\gamma -1}}}\right]\\&\approx {\frac {\gamma +1}{12\gamma ^{2}}}\left({\frac {p_{2}-p_{1}}{p_{1}}}\right)^{3}\\&\approx {\frac {\gamma +1}{12\gamma ^{2}}}\left[{\frac {\rho _{1}w_{1}^{2}}{p_{1}}}\left(1-{\frac {w_{2}}{w_{1}}}\right)\right]^{3}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/128f390d30e85d19af260e60985d609eada957bd)












