Partitionsalgebra

Partitionsalgebra är en associativ algebra med en bas av set-partitionsdiagram och multiplikation som ges genom diagramsammansättning . Dess subalgebror inkluderar diagramalgebror som Brauer-algebra , Temperley-Lieb-algebra eller gruppalgebra för den symmetriska gruppen . Representationer av partitionsalgebra är byggda från uppsättningar av diagram och från representationer av den symmetriska gruppen.

Definition

Diagram

En partition med $2k$ element märkta $1,{\bar {1}},2,{\bar {2}} ,\dots ,k,{\bar {k}}$ representeras som ett diagram, med linjer som förbinder element i samma delmängd. I följande exempel är delmängden $\{{\bar {1}},{\bar {4}},{\bar {5}},6\ }$ ger upphov till raderna ${\bar {1}}-{\bar {4}},{\bar {4}}- {\bar {5}},{\bar {5}}-6$ , och kan på motsvarande sätt representeras av raderna ${\displaystyle {\bar {1}}-6,{\bar {4}}-6,{\bar {5}}-6,{\bar {1}}-{\bar {5}}} ($ till exempel) .

För $n\in \mathbb {C}$ och $k\in \mathbb {N} ^{*}$ , partitionsalgebra $P_ {k}(n)$ definieras av en $\mathbb {C}$ -bas gjord av partitioner, och en multiplikation som ges av diagramsammansättning. Det sammanlänkade diagrammet kommer med en faktor $n^{D}$ , där $D$ är antalet anslutna komponenter som är bortkopplade från de övre och nedre elementen.

Generatorer och relationer

Partitionsalgebra $P_{k}(n)$ genereras av $3k-2$ element av typen

Dessa generatorer lyder relationer som inkluderar

$s_{i}^{2}=1\quad ,\quad s_{i}s_{i+1}s_{i}=s_{i+1}s_{i}s_{i+1}\ quad ,\quad p_{i}^{2}=np_{i}\quad ,\quad b_{i}^{2}=b_{i}\quad ,\quad p_{i}b_{i}p_{ i}=p_{i}$

Andra element som är användbara för att generera subalgebra inkluderar

När det gäller de ursprungliga generatorerna är dessa element

$e_{i}=b_{i}p_{i}p_{i+1 }b_{i}\quad ,\quad l_{i}=s_{i}p_{i}\quad ,\quad r_{i}=p_{i}s_{i}$

Egenskaper

Partitionsalgebra $P_{k}(n)$ är en associativ algebra . Den har en multiplikativ identitet

Partitionsalgebra $P_{k}(n)$ är halvenkel för $n\in \mathbb {C} -\ {0,1,\dots ,2k-2\}$ . För två $n,n'$ i denna uppsättning, algebrorna $P_{k}(n)$ och $P_{k }(n')$ är isomorfa.

Partitionsalgebra är ändlig dimensionell, med $\dim P_{k}(n)=B_{2k}$ (ett klocknummer ).

Subalgebras

Åtta subalgebror

Subalgebror för partitionsalgebra kan definieras av följande egenskaper:

• Om de är plana dvs om linjer kan korsas i diagram.
• Om delmängder tillåts ha någon storlek $1,2,\dots ,2k$ , eller storlek $1,2$ , eller bara storlek $2$ .
• Oavsett om vi tillåter topp- och bottenrader, eller bara topp-bottenrader. I det senare fallet saknas parametern ${\displaystyle n} , eller kan elimineras med$$p_{i}\to {\frac {1}{n}}p_{i }$ .

Att kombinera dessa egenskaper ger upphov till 8 icke-triviala subalgebror, förutom själva partitionsalgebra:

Notation	namn	Generatorer	Dimensionera	Exempel
$P_{k}(n)$	Dela	$s_{i},p_{i},b_{i}$	$B_{2k}$
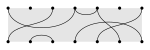
$PP_{k}(n)$	Plan partition	$p_{i},b_{i}$	${\frac {1}{2k+1}}{\binom {4k}{2k}}$
$RB_{k}(n)$	Rook Brauer	$s_{i},e_{i},p_{i}$	$\sum _{\ell =0}^{k}{\binom {2k}{2\ell }}(2\ell -1)!!$
$M_{k}(n)$	Motzkin	$e_{i},l_{i},r_{i}$	$\sum _{\ell =0}^{k}{\frac {1}{\ell +1}}{\ binom {2\ell }{\ell }}{\binom {2k}{2\ell }}$
$B_{k}(n)$	Brauer	$s_{i},e_{i}$	$(2k-1)!!$
$TL_{k}(n)$	Temperley–Lieb	$e_{i}$	${\frac {1}{k+1}}{\binom {2k}{k}}$
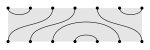
$R_{k}$	Råka	$s_{i},p_{i}$	$\sum _{\ell =0}^{k}{\binom {k}{\ell }}^{2}\ell !$
$PR_{k}$	Plana torn	$l_{i},r_{i}$	${\binom {2k}{k}}$
$\mathbb {C} S_{k}$	Symmetrisk grupp	$s_{i}$	$k!$

Den symmetriska gruppen algebra $\mathbb {C} S_{k}$ är gruppringen för den symmetriska gruppen $S_{k}$ över $\mathbb {C}$ . Motzkin-algebra kallas ibland den utspädda Temperley–Lieb-algebra i fysiklitteraturen.

Egenskaper

De angivna subalgebrerna är halvenkla för $n\in \mathbb {C} -\{0,1,\dots ,2k-2\}$ .

Inklusioner av plana i icke-plana algebror:

$PP_{ k}(n)\subset P_{k}(n)\quad ,\quad M_{k}(n)\subset RB_{k}(n)\quad ,\quad TL_{k}(n)\subset B_ {k}(n)\quad ,\quad PR_{k}\subset R_{k}$

Inklusioner från begränsningar för delmängdsstorlek:

$B_{ k}(n)\subset RB_{k}(n)\subset P_{k}(n)\quad ,\quad TL_{k}(n)\subset M_{k}(n)\subset PP_{k} (n)\quad ,\quad \mathbb {C} S_{k}\subset R_{k}$

Inklusioner från att tillåta topp-och botten-rader:

$R_{k}\subset RB_{k}(n)\quad ,\quad PR_{k}\subset M_{k}(n)\quad ,\quad \mathbb {C} S_{k}\subset B_{k}(n)$

Vi har isomorfismen:

$PP_{k}(n^{2})\cong TL_{2k}(n)\quad ,\quad \left\{{\begin{array}{l}p_{i}\mapsto ne_{2i-1}\\b_{i}\mapsto {\frac {1 }{n}}e_{2i}\end{array}}\right.$

Mer subalgebra

Förutom de åtta subalgebrorna som beskrivs ovan har andra subalgebror definierats:

• Den helt utbredda partitionen subalgebra ${\text{prop}}P_{k}$ genereras av diagram vars block alla sprider sig, dvs partitioner vars delmängder alla innehåller topp- och bottenelement. Dessa diagram från den dubbla symmetriska inversa monoiden, som genereras av $s_{i},b_{i}p_{i+1}b_{i+1}$ .
• Kvasipartitionsalgebran $QP_{k}(n)$ genereras av delmängder med storleken minst två. Dess generatorer är $s_{i},b_{i},e_{i}$ och dess dimension är $1+\sum _{j=1}^{2k}(-1)^{j-1}B_{2k-j}$ .
• Den enhetliga blockpermutationsalgebra $U_{k}$ genereras av delmängder med lika många toppelement som bottenelement. Den genereras av $s_{i},b_{i}$ .

En algebra med ett halvt heltalsindex $k+{\frac {1}{2}}$ definieras från partitioner med $2k+2$ element genom att kräva att $k+1$ och ${\overline {k+1}}$ är i samma delmängd. Till exempel genereras ${\displaystyle P_{k+{\frac {1}{2}}}} av$$s_{ i\leq k-1},b_{i\leq k},p_{i\leq k}$ så att $P_{k}\subset P_{ k+{\frac {1}{2}}}\subset P_{k+1}$ och $\dim P_{k+{\frac {1} {2}}}=B_{2k+1}$ .

Periodiska subalgebror genereras av diagram som kan ritas på en ringform utan linjekorsningar. Sådana subalgebror inkluderar ett översättningselement $u=$ så att $u^{k}=1$ . Översättningselementet och dess potenser är de enda kombinationerna av $s_{i}$ som hör till periodiska subalgebra.

Framställningar

Strukturera

För ett heltal $0\leq \ell \leq k$ , låt $D_{\ell }$ vara uppsättningen av partitioner av $k+\ell$ element $1,2,\dots ,k$ (nederst) och ${\bar {1}},{\bar {2}} ,\dots ,{\bar {\ell }}$ (överst), så att inga två toppelement är i samma delmängd och inget toppelement är ensamt. Sådana partitioner representeras av diagram utan topp-top-linjer, med minst en linje för varje toppelement. Till exempel, i fallet $k=12,\ell =5$ :

Partitionsdiagram verkar på $D_{\ell }$ från botten, medan den symmetriska gruppen $S_{\ell }$ verkar från toppen. För varje Specht-modul $V_{\lambda }$ av $S_{\ell }$ (med därför $|\lambda |=\ell$ ), definierar vi representationen av $P_{k}(n)$

${\mathcal {P}}_{\lambda }=\mathbb {C} D_{|\lambda |}\otimes _{\mathbb {C} S_{|\lambda |}}V_{\lambda } \ .$

Dimensionen av denna representation är

$\dim {\mathcal {P}}_{\lambda }=f_{\lambda }\sum _{\ell =|\lambda |}^{k }\left\{{k \atop \ell }\right\}{\binom {\ell }{|\lambda |}}\ ,$

där $\left\{{k \atop \ell }\right\}$ är ett Stirlingtal av det andra slaget , ${\binom {\ell }{ |\lambda |}}$ är en binomial koefficient och $f_{\lambda }=\dim S_{\lambda }$ ges av kroklängdsformeln .

En grund för ${\mathcal {P}}_{\lambda }$ kan beskrivas kombinatoriskt i termer av set-partitionstabeller: Unga tablåer vars rutor är fyllda med blocken av en uppsättningspartition.

Om vi ​​antar att $P_{k}(n)$ är halvenkel, är representationen ${\mathcal {P}}_{\lambda }$ irreducerbar och mängden irreducerbar finit -dimensionella representationer av partitionsalgebra är

${\text{Irrep}}\left(P_{k}(n)\right)=\left\{{\mathcal {P}}_{\lambda }\right\}_{0\leq | \lambda |\leq k}\ .$

Representationer av subalgebra

Representationer av icke-plana subalgebra har liknande strukturer som representationer av partitionsalgebra. Till exempel Brauer-Specht-modulerna i Brauer-algebra byggda av Specht-moduler och vissa uppsättningar av partitioner.

I fallet med plana subalgebrer förhindrar planaritet icke-triviala permutationer, och Specht-moduler visas inte. Till exempel parametriseras en standardmodul i Temperley–Lieb algebra av ett heltal $0\leq \ell \leq k$ med $\ell \equiv k{\bmod {2}}$ , och en bas ges helt enkelt av en uppsättning partitioner.

Följande tabell listar de irreducerbara representationerna av partitionsalgebra och åtta subalgebror.

Algebra	Parameter	Betingelser	Dimensionera
$P_{k}(n)$	$\lambda$	$0\leq |\lambda |\leq k$	$f_{\lambda }\sum _{\ell =|\lambda |}^{k}\left\{{k \atop \ell }\right\} {\binom {\ell }{|\lambda |}}$
$PP_{k}(n)$	$\ell$	$0\leq \ell \leq k$	${\binom {2k}{k+\ell }}-{\binom {2k}{k+\ell +1}}$
$RB_{k}(n)$	$\lambda$	$0\leq |\lambda |\leq k$	$f_{\lambda }{\binom {k}{|\lambda |}}\sum _{m=0}^{\left\lfloor {\frac {k-|\lambda |}{2}} \höger\rgolv }{\binom {k-|\lambda |}{2m}}(2m-1)!!$
$M_{k}(n)$	$\ell$	$0\leq \ell \leq k$	$\sum _{m=0}^{\left \lfloor {\frac {k-\ell }{2}}\right\rfloor }{\binom {k}{\ell +2m}}\left\{{\binom {\ell +2m}{m}} -{\binom {\ell +2m}{m-1}}\right\}$
$B_{k}(n)$	$\lambda$	${\begin{array}{c}0\leq |\lambda |\leq k\\|\lambda |\equiv k{\bmod {2}}\end{array}}$	$f_{\lambda }{\binom {k}{|\lambda |}}(k-|\lambda |-1)!!$
$TL_{k}(n)$	$\ell$	${\begin{array}{c}0\leq \ell \leq k\\\ell \equiv k{\bmod {2}}\end{array}}$	${\binom {k}{\frac {k+\ell }{2}}}-{\binom {k}{\frac { k+\ell +2}{2}}}$
$R_{k}$	$\lambda$	$0\leq |\lambda |\leq k$	$f_{\lambda }{\binom {k}{|\lambda |}}$
$PR_{k}$	$\ell$	$0\leq \ell \leq k$	${\binom {k}{\ell }}$
$\mathbb {C} S_{k}$	$\lambda$	$|\lambda |=k$	$f_{\lambda }$

De irreducerbara representationerna av ${\text{prop}}P_{k}$ indexeras av partitioner så att $0<|\lambda |\leq k$ och deras mått är $f_{\lambda }\left\{{k \atop |\lambda |}\right\}$ . De irreducerbara representationerna av $QP_{k}$ indexeras av partitioner så att $0\leq |\lambda |\leq k$ . De irreducerbara representationerna av $U_{k}$ indexeras av sekvenser av partitioner.

Schur-Weyl dualitet

Antag $n\in \mathbb {N} ^{*}$ . För $V$ a $n$ -dimensionellt vektorrum med bas $v_{1},\dots ,v_{n}$ finns det en naturlig verkan av partitionsalgebra $P_{k}(n)$ på vektorrummet $V^{\otimes k}$ . Denna åtgärd definieras av matriselementen för en partition ${\displaystyle \{1,{\bar {1}},2 ,{\bar {2}},\dots ,k,{\bar {k}}\}=\sqcup _{h}E_{h}} i$ basen ${ \displaystyle (v_{j_{1}}\otimes \cdots \otimes v_{j_{k}})}$ :

$\left(\sqcup _{h}E_{h}\right)_{j_{1},j_{2},\dots ,j_{k}}^{j_{\bar {1}}, j_{\bar {2}},\dots ,j_{\bar {k}}}=\mathbf {1} _{r,s\in E_{h}\implies j_{r}=j_{s}} \ .$

Detta matriselement är ett om alla index som motsvarar en given partitionsdelmängd sammanfaller, och noll annars. Till exempel är handlingen hos en Temperley–Lieb-generator

$e_{i}\left(v_{j_{1}}\otimes \cdots \otimes v_{j_{i}}\otimes v_{j_{i+1}}\otimes \cdots \otimes v_{j_ {k}}\right)=\delta _{j_{i},j_{i+1}}\summa _{j=1}^{n}v_{j_{1}}\otimes \cdots \otimes v_ {j}\otimes v_{j}\otimes \cdots \otimes v_{j_{k}}\ .$

Dualitet mellan partitionsalgebra och den symmetriska gruppen

Låt $n\geq 2k$ vara heltal. Låt oss ta $V$ som den naturliga permutationsrepresentationen av den symmetriska gruppen $S_{n}$ . Denna $n$ -dimensionella representation är summan av två irreducerbara representationer: standardrepresentationerna och trivialrepresentationerna, $V=[n-1,1]\ oplus [n]$ .

är partitionsalgebra $P_{k}(n)$ centraliseraren för åtgärden av $S_{n}$ på tensorproduktutrymmet $V^ {\otimes k}$ ,

$P_{k}(n)\cong {\text{End}}_{S_{n}}\left(V^{\otimes k}\right)\ .$

Dessutom, som en bimodul över $P_{k}(n)\ gånger S_{n}$ sönderdelas tensorproduktutrymmet till irreducerbara representationer som

$V^{\otimes k}=\bigoplus _{0\leq |\lambda |\leq k}{\mathcal {P}}_{\lambda }\otimes V_{[n-| \lambda |,\lambda ]}\ ,$

där $[n-|\lambda |,\lambda ]$ är ett Young diagram av storlek $n$ byggt genom att lägga till en första rad till $\lambda$ och $V_{[n-|\lambda |,\lambda ]}$ är motsvarande Specht-modul för $S_{n}$ .

Dualiteter som involverar subalgebra

Dualiteten mellan den symmetriska gruppen och partitionsalgebra generaliserar den ursprungliga Schur-Weyl-dualiteten mellan den allmänna linjära gruppen och den symmetriska gruppen. Det finns andra generaliseringar. I de relevanta tensorproduktutrymmena skriver vi $V_{n}$ för en irreducerbar $n$ -dimensionell representation av den första gruppen eller algebra:

Tensor produktutrymme	Grupp eller algebra	Dubbel algebra eller grupp	Kommentarer
$\left(V_{n-1}\oplus V_{1}\right)^{\otimes k}$	$S_{n}$	$P_{k}(n)$	Dualiteten för den fullständiga partitionsalgebra
$\left(V_{n-2}\oplus V_{1}\oplus V_{1}\right)^{\otimes k}$	$S_{n-1}$	$P_{k+{\frac {1}{2}}}(n)$	Fall av en partitionsalgebra med ett halvt heltalsindex
$V_{n}^{\otimes k}$	$GL_{n}(\mathbb {C} )$	$S_{k}$	Den ursprungliga Schur-Weyl-dualiteten
$V_{n}^{\otimes k}$	$O(n)$	$B_{k}(n)$	Dualitet mellan den ortogonala gruppen och Brauer algebra
$\left(V_{n}\oplus V_{1}\right)^{\otimes k}$	$O(n)$	$RB_{k}(n+1)$	Dualitet mellan den ortogonala gruppen och tornet Brauer algebra
$V_{n}^{\otimes k}$	$R_{n}$	${\text{prop}}P_{k}$	Dualitet mellan tornalgebra och den helt utbredda partitionsalgebra
$V_{2}^{\otimes k}$	$gl(1|1)$	$PR_{k-1}$	Dualitet mellan en Lie superalgebra och den plana tornalgebra
$V_{n-1}^{\otimes k}$	$S_{n}$	$QP_{k}(n)$	Dualitet mellan den symmetriska gruppen och kvasipartitionsalgebra
$V_{n}^{\otimes r}\otimes \left(V_{n}^{*}\right)^{\otimes s}$	$GL_{n}(\mathbb {C} )$	$B_{r,s}(n)$	Dualitet som involverar den muromgärdade Brauer algebra .

Vidare läsning

•   Kauffman, Louis H. (1991). Knutar och fysik . World Scientific. ISBN 978-981-02-0343-6 .
•   Kauffman, Louis H. (1990). "En invariant av vanlig isotopi" . Transaktioner från American Mathematical Society . 318 (2): 417–471. doi : 10.1090/S0002-9947-1990-0958895-7 . ISSN 0002-9947 .