Brauer algebra

I matematik är en Brauer-algebra en associativ algebra som introducerades av Richard Brauer i samband med representationsteorin för den ortogonala gruppen . Den spelar samma roll som den symmetriska gruppen gör för representationsteorin för den allmänna linjära gruppen i Schur–Weyl-dualitet .

Strukturera

Brauer algebra ${\mathfrak {B}}_{n}(\delta )$ är en $\mathbb {Z} [\delta ]$ -algebra beroende på valet av ett positivt heltal $n$ . Här $\delta$ en obestämd, men i praktiken är $\delta$ ofta specialiserad på dimensionen av den fundamentala representationen av en ortogonal grupp $O(\delta )$ . Brauer algebra har dimensionen

$\dim {\mathfrak {B}}_{n}(\delta )={\frac {(2n)!}{ 2^{n}n!}}=(2n-1)!!=(2n-1)(2n-3)\cdots 5\cdot 3\cdot 1$

Diagrammatisk definition

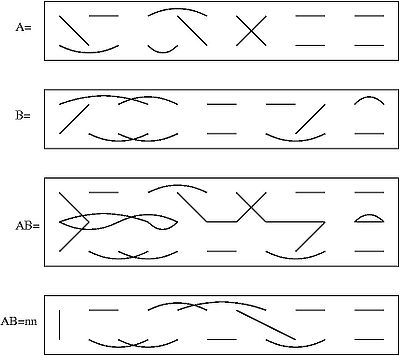
Produkten av 2 baselement A och B i Brauer-algebra med n = 12

En bas av ${\mathfrak {B}}_{n}(\delta )$ består av alla parningar på en uppsättning av $2n$ element ${\displaystyle X_{1},...,X_{n},Y_{1},...,Y_{n}} (det$ vill säga alla perfekta matchningar av en komplett graf $K_{n}$ : två av de $2n$ elementen kan matchas med varandra, oavsett deras symboler). Elementen $X_{i}$ skrivs vanligtvis i en rad, med elementen $Y_{i}$ under dem.

Produkten av två baselement $A$ och $B$ erhålls genom sammanlänkning: först identifieras slutpunkterna i den nedre raden av $A$ och den översta raden i $B$ (Figur AB i diagrammet), radera sedan ändpunkterna i den mellersta raden och sammanfoga ändpunkterna i de återstående två raderna om de är sammanfogade, direkt eller via en bana, i AB ( Figur AB =nn i diagrammet). Därmed tas alla slutna slingor i mitten av AB bort. Produkten $A\cdot B$ av baselementen definieras sedan till att vara baselementet som motsvarar den nya parningen multiplicerat med $\delta ^{r}$ där $r$ är antalet raderade loopar. I exemplet $A\cdot B=\delta ^{2}AB$ .

Generatorer och relationer

${\mathfrak {B}}_{n}(\delta )$ kan också definieras som $\mathbb {Z} [\delta ]$ -algebra med generatorer $s_{1},\ldots ,s_{n-1},e_{1},\ldots,e_{n- 1}$ som uppfyller följande relationer:

• Relationer för den symmetriska gruppen :

$s_{i}^{2}=1$

$s_{i}s_{j}=s_{j} s_{i}$ när som helst $|ij|>1$

$s_{i}s_{i+1}s_{i}=s_{ i+1}s_{i}s_{i+1}$

• Nästan idempotent relation:

$e_{i}^{2}=\delta e_{i}$

• Kommutering:

$e_{i}e_{j}=e_{j}e_{i}$

$s_{i}e_{j}=e_ {j}s_{i}$

när som helst $|ij|>1$

• Tangle relations

$e_{i}e_{i\pm 1}e_{i}=e_{i}$

$s_{i}s_{i\pm 1}e_{i}=e_{i\pm 1}e_{i}$

${\displaystyle e_{i}s_{i\pm 1}s_{i}=e_{i}e_{i\pm 1}} Ovridning$

• :

${\displaystyle s_{i}e_{i}=e_{i}s_{i}=e_{i}} : e i s i ± 1$ e

$s_ {i\pm 1}e_{i}=e_{i}}$

I denna presentation representerar $s_{i}$ diagrammet där $X_{k}$ alltid är kopplad till $Y_{k}$ direkt under det förutom ${ \displaystyle X_{i}}$ och $X_{i+1}$ som är kopplade till $Y_{i+1}$ och $Y_{i}$ respektive. På liknande sätt $e_{i}$ diagrammet där $X_{k}$ alltid är kopplad till $Y_{k}$ direkt under det förutom $X_{i}$ kopplas till $X_{i+1}$ och $Y_{i}$ till $Y_{i+1}$ .

Grundläggande egenskaper

Brauer-algebra är en subalgebra till partitionsalgebra .

Brauer-algebra ${\mathfrak {B}}_{n}(\delta )$ är halvenkel om $\delta \in \mathbb {C} -\{0,\pm 1,\pm 2,\dots ,\pm n\}$ .

Subalgebra för ${\mathfrak {B}}_{n}(\delta )$ som genereras av generatorerna $s_{i}$ är gruppalgebra för den symmetriska gruppen $S_{n}$ .

Subalgebra för ${\mathfrak {B}}_{n}(\delta )$ som genereras av generatorerna $e_{i}$ är Temperley-Lieb algebra $TL_{n}(\delta)$ .

Brauer-algebra är en cellulär algebra .

För en parning $A$ låt $n(A)$ vara antalet slutna slingor som bildas genom att identifiera $X_{i}$ med $Y_{i }$ för alla $i=1,2,\dots ,n$ : sedan Jones-spåret ${\text{Tr }}(A)=\delta ^{n(A)}$ lyder ${\text{Tr}}(AB)={\text{Tr}}( BA)$ dvs det är verkligen ett spår .

Framställningar

Brauer-Specht-moduler

Brauer-Specht-moduler är ändliga dimensionella moduler av Brauer-algebra. Om $\delta$ är sådan att ${\mathfrak {B}}_{n}(\delta )$ är halvenkel, bildar de en komplett uppsättning enkla moduler av ${\mathfrak {B}}_{n}(\delta )$ . Dessa moduler parametriseras av partitioner , eftersom de är byggda från Specht-modulerna i den symmetriska gruppen , som själva parametriseras av partitioner.

För $0\leq \ell \leq n$ med ${\displaystyle \ell \equiv n{\bmod {2}}},$ låt $B_{ n,\ell }$ vara uppsättningen av perfekta matchningar av $n+\ell$ element ${\displaystyle X_{1},\dots , X_{n},Y_{1},\dots ,Y_{\ell }},$ så att $Y_{j}$ matchas med ett av de $n$ elementen $X_{1},\dots ,X_{n}$ . För valfri ring ${\displaystyle k} är$ mellanslag $kB_{n,\ell }$ en vänster ${\mathfrak {B}}_{n} (\delta )$ -modul, där baselement för ${\mathfrak {B}}_{n}(\delta )$ verkar genom grafsammansättning. (Denna åtgärd kan producera matchningar som bryter mot begränsningen som $Y_{1},\dots ,Y_{\ell }$ inte kan matcha med varandra: sådana grafer måste ändras.) Dessutom , utrymmet $kB_{n,\ell }$ är en höger $S_{\ell }$ -modul.

Givet en Specht-modul $V_{\lambda }$ av $kS_{\ell }$ , där $\lambda$ är en partition av $\ell$ (dvs. $|\lambda |=\ell$ ), motsvarande Brauer-Specht-modul för ${\mathfrak {B}}_{n}(\delta )$ är

$W_{\lambda }=kB_{n,|\lambda |}\otimes _{kS_{|\lambda |}}V_{\ lambda }\qquad {\big (}|\lambda |\leq n,|\lambda |\equiv n{\bmod {2}}{\big )}$

En grund för denna modul är uppsättningen av element ${\displaystyle b\otimes v} ,$ där $b\in B_{n,|\lambda |}$ är sådan att $|\lambda |$ linjer som slutar på elementen $Y_{j}$ korsas inte, och $v$ tillhör en bas av $V_{\lambda }$ . Dimensionen är

$\dim(W_{\lambda })={\binom {n}{|\lambda |}}(n-|\lambda |-1)!!\dim(V_{\ lambda })$

dvs produkten av en binomial koefficient , en dubbelfaktor och dimensionen av motsvarande Specht-modul, som ges av kroklängdsformeln .

Schur-Weyl dualitet

Låt $V=\mathbb {R} ^{d}$ vara ett euklidiskt vektorrum med dimensionen $d$ , och $O (V)=O(d,\mathbb {R} )$ motsvarande ortogonala grupp. Skriv sedan $B_{n}(d)$ för inriktningen $\mathbb {R} \otimes _{\mathbb {Z} [ \delta ]}{\mathfrak {B}}_{n}(\delta )$ där $\delta$ verkar på $\mathbb {R}$ genom multiplikation med $d$ . Tensorkraften $}}$$V^{\otimes n}:=\underbrace {V\otimes \cdots \otimes V} _{n{\text{ gånger$ } är naturligtvis en $B_{n}(d)$ - modul : $s_{i}$ fungerar genom att byta i { $displaystyle i}$ th och ${\displaystyle (i+1)}:$ e tensorfaktorn och $e_{i}$ verkar genom sammandragning följt av expansion i ${\displaystyle i}:$ ten och ${\displaystyle (i) +1)}:$ e tensorfaktorn, dvs $e_{i}$ fungerar som

$v_{1}\otimes \cdots \otimes v_{i-1}\otimes {\Big (}v_{i}\otimes v_{i+1 }{\Big )}\otimes \cdots \otimes v_{n}\mapsto v_{1}\otimes \cdots \otimes v_{i-1}\otimes \left(\langle v_{i},v_{i+ 1}\rangle \sum _{k=1}^{d}(w_{k}\otimes w_{k})\right)\otimes \cdots \otimes v_{n}$

där $​​{\displaystyle w_{1},\ldots ,w_{d}}$ är någon ortonormal grund för $V$ . (Summan är i själva verket oberoende av valet av denna grund.)

Denna åtgärd är användbar i en generalisering av Schur-Weyl-dualiteten : om $d\geq n$ , bilden av $B_{n}(d)$ inuti $\operatorname {End} (V^{\otimes n})$ är centraliseraren för $O(V)$ inuti $\ operatornamn {End} (V^{\otimes n})$ , och omvänt är bilden av $O(V)$ centraliseraren för $B_{n}(d )$ . Tensoreffekten $V^{\otimes n}$ är därför både en $O(V)$ - och en $B_{n}(d )$ -modul och uppfyller

$V^{\otimes n}=\bigoplus _{\lambda }U_{\lambda }\boxtimes W_{\lambda }$

där $\lambda$ körs över en delmängd av partitionerna så att $|\lambda |\leq n$ och $|\lambda |\equiv n{\bmod {2}}$$) {\displaystyle O(V)}$ U $\displaystyle U_{\lambda }}$ är en irreducerbar - modul, och $W_{\lambda }$ är en Brauer-Specht-modul av $B_{n}(d)$ .

Det följer att Brauer-algebra har en naturlig verkan på rymden av polynom på ${\displaystyle V^{n}} ,$ som pendlar med verkan av den ortogonala gruppen.

Om $\delta$ är ett negativt jämnt heltal, relateras Brauer-algebra av Schur-Weyl-dualitet till den symplektiska gruppen ${\text{Sp}}_{-\delta } (\mathbb {C} )$ , snarare än den ortogonala gruppen.

Walled Brauer algebra

Den muromgärdade Brauer-algebran ${\mathfrak {B}}_{r,s}(\delta )$ är en subalgebra av ${\mathfrak { B}}_{r+s}(\delta)$ . Diagrammatiskt består den av diagram där de enda tillåtna parningarna är av typerna $X_{i\leq r}-X_{j>r}$ , $Y_{i\leq r}-Y_{j>r}$ , $X_{i\leq r}-Y_{j\leq r}$ , $X_{i>r}-Y_{j>r}$ . Detta motsvarar att ha en vägg som skiljer $X_{i\leq r},Y_{i\leq r}$ från $X_ {i>r},Y_{i>r}$ och kräver att $XY$ -par korsar väggen medan $XX,YY$ -par inte gör det.

Den murade Brauer-algebran genereras av $\{s_{i}\}_{1\leq i\leq r+ s-1,i\neq r}\cup \{e_{r}\}$ . Dessa generatorer följer de grundläggande relationerna för ${\mathfrak {B}}_{r+s}(\delta )$ som involverar dem, plus de två relationerna

$e_{r}s_{r+1}s_{r-1}e_{r}s_{r-1}=e_{r }s_{r+1}s_{r-1}e_{r}s_{r+1}\quad ,\quad s_{r-1}e_{r}s_{r+1}s_{r-1} e_{r}=s_{r+1}e_{r}s_{r+1}s_{r-1}e_{r}$

(I ${\mathfrak {B}}_{r+s}(\delta )$ följer dessa två relationer från de grundläggande relationerna.)

För $\delta$ ett naturligt heltal, låt $V$ vara den naturliga representationen av den allmänna linjära gruppen $GL_{\delta }(\mathbb {C} )$ . Den muromgärdade Brauer-algebran ${\mathfrak {B}}_{r,s}(\delta )$ har en naturlig verkan på ${\displaystyle V^{\otimes r}\otimes (V^{*})^{\otimes s}} ,$ som av Schur-Weyl-dualitet relateras till verkan av $GL_{\delta } (\mathbb {C} )$ .

Se även

• Birman–Wenzl algebra , en deformation av Brauer algebra.