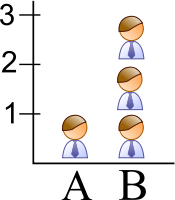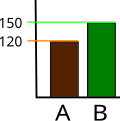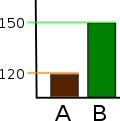Missvisande graf
| Del av en serie om statistik |
| Data och informationsvisualisering |
|---|
| Stora dimensioner |
| Viktiga siffror |
| Informationsgrafiska typer |
| Relaterade ämnen |
Inom statistik är en vilseledande graf , även känd som en förvrängd graf , en graf som missvisar data , vilket utgör ett missbruk av statistik och med resultatet att en felaktig slutsats kan härledas från den.
Grafer kan vara vilseledande genom att vara alltför komplexa eller dåligt konstruerade. Även när de är konstruerade för att visa egenskaperna hos deras data korrekt, kan grafer bli föremål för olika tolkningar, eller oavsiktliga typer av data kan till synes och i slutändan felaktigt härledas.
Vilseledande grafer kan skapas avsiktligt för att hindra korrekt tolkning av data eller av misstag på grund av obekantskap med grafprogram , felaktig tolkning av data eller på grund av att data inte kan förmedlas korrekt. Vilseledande grafer används ofta i falsk reklam . En av de första författarna som skrev om vilseledande grafer var Darrell Huff , utgivare av 1954 års bok How to Lie with Statistics .
Fältet datavisualisering beskriver sätt att presentera information som undviker att skapa vilseledande grafer.
Vilseledande grafmetoder
Den [en vilseledande graf] är mycket effektivare, men eftersom den inte innehåller några adjektiv eller adverb för att förstöra illusionen av objektivitet, det finns inget som någon kan fästa vid dig.
— Hur man ljuger med statistik (1954)
Det finns många sätt på vilka en vilseledande graf kan konstrueras.
Överdriven användning
Användningen av grafer där de inte behövs kan leda till onödig förvirring/tolkning. Generellt gäller att ju mer förklaring en graf behöver, desto mindre behövs själva grafen. Grafer förmedlar inte alltid information bättre än tabeller.
Partisk märkning
Användningen av partiska eller laddade ord i diagrammets titel, axeletiketter eller bildtext kan göra läsaren olämplig.
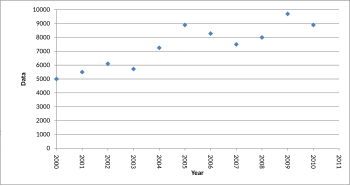
Tillverkade trender
På samma sätt kan ett försök att dra trendlinjer genom okorrelerade data vilseleda läsaren att tro att det finns en trend där det inte finns någon. Detta kan både vara resultatet av avsiktligt försök att vilseleda läsaren eller på grund av fenomenet illusorisk korrelation .
Tårtdiagram
- Att jämföra cirkeldiagram av olika storlekar kan vara vilseledande eftersom människor inte kan avläsa den jämförande arean av cirklar korrekt.
- Användningen av tunna skivor, som är svåra att urskilja, kan vara svår att tolka.
- Användningen av procentsatser som etiketter på ett cirkeldiagram kan vara vilseledande när urvalsstorleken är liten.
- Att göra ett cirkeldiagram i 3D eller lägga till en lutning kommer att göra tolkningen svår på grund av förvrängd perspektiveffekt . Stapeldiagram med cirkeldiagram där höjden på skivorna varieras kan förvirra läsaren.
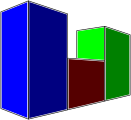
Jämföra cirkeldiagram
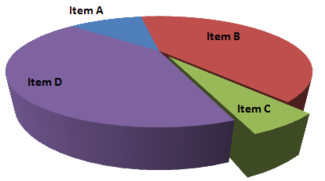
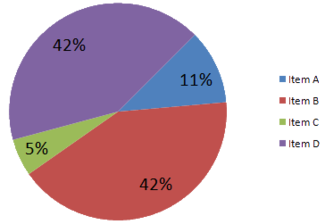
Att jämföra data på barcharts är i allmänhet mycket lättare. I bilden nedan är det mycket svårt att avgöra var den blå sektorn är större än den gröna sektorn på piecharts.
3D cirkeldiagram skivperspektiv
Ett perspektivdiagram (3D) används för att ge diagrammet ett 3D -utseende. Den tredje dimensionen används ofta av estetiska skäl och förbättrar inte läsningen av data; tvärtom är dessa intrigar svåra att tolka på grund av den förvrängda effekten av perspektiv som är förknippad med den tredje dimensionen. Användningen av överflödiga dimensioner som inte används för att visa data av intresse avråds för diagram i allmänhet, inte bara för cirkeldiagram. I ett 3D-cirkeldiagram verkar skivorna som är närmare läsaren vara större än de på baksidan på grund av vinkeln de presenteras med. Denna effekt gör läsare mindre presterande när det gäller att bedöma den relativa storleken på varje skiva när de använder 3D än 2D
Objekt C verkar vara minst lika stort som objekt A i det missvisande cirkeldiagrammet, medan det i själva verket är mindre än hälften så stort. Objekt D ser mycket större ut än objekt B, men de har samma storlek.
Edward Tufte , en framstående amerikansk statistiker, noterade varför tabeller kan föredras framför cirkeldiagram i The Visual Display of Quantitative Information :
Tabeller är att föredra framför grafik för många små datamängder. Ett bord är nästan alltid bättre än ett dumt cirkeldiagram; det enda som är värre än ett cirkeldiagram är flera av dem, för då ombeds tittaren att jämföra kvantiteter som befinner sig i rumslig oordning både inom och mellan pajer – med tanke på deras låga datatäthet och misslyckande att ordna siffror längs en visuell dimension, cirkeldiagram bör aldrig användas.
Felaktig skalning
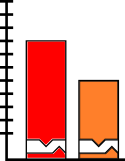
Användning av piktogram i stapeldiagram bör inte skalas enhetligt, eftersom detta skapar en perceptuellt missvisande jämförelse. Området för piktogrammet tolkas istället för endast dess höjd eller bredd. Detta gör att skalningen gör att skillnaden ser ut att vara kvadratisk.
I det felaktigt skalade piktogramstapeldiagrammet är bilden för B faktiskt 9 gånger så stor som A.
Den upplevda storleken ökar vid skalning.
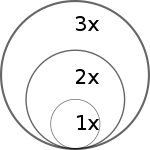
Effekten av felaktig skalning av piktogram exemplifieras ytterligare när piktogrammet har 3 dimensioner, i vilket fall effekten är kubad.
Grafen över husförsäljning (till vänster) är missvisande. Det verkar som att bostadsförsäljningen har vuxit åttafaldigt under 2001 jämfört med föregående år, medan den faktiskt har vuxit fördubblas. Dessutom är antalet försäljningar inte specificerat.
Ett felaktigt skalat piktogram kan också tyda på att själva föremålet har ändrats i storlek.
Förutsatt att bilderna representerar ekvivalenta kvantiteter visar den missvisande grafen att det finns fler bananer eftersom bananerna upptar mest yta och ligger längst till höger.
Logaritmisk skalning
Logaritmiska (eller log) skalor är ett giltigt sätt att representera data. Men när de används utan att vara tydligt märkta som loggvågar eller visas för en läsare som inte är bekant med dem, kan de vara vilseledande. Loggskalor sätter datavärdena i termer av ett valt nummer (basen av loggen) till en viss effekt. Basen är ofta e (2,71828...) eller 10. Loggskalor kan till exempel ge en höjd på 1 för ett värde på 10 i data och en höjd på 6 för ett värde på 1 000 000 (10 6 ) i data . Log skalor och varianter används ofta, till exempel för vulkaniskt explosivitetsindex, Richterskalan för jordbävningar, storleken på stjärnor och pH för sura och alkaliska lösningar. Även i dessa fall kan loggskalan göra data mindre uppenbara för ögat. Ofta är anledningen till att logga skalor används att grafens författare vill visa väldigt olika skalor på samma axel. Utan stockskalor blir det visuellt opraktiskt att jämföra mängder som 10 3 mot 10 9 . En graf med en loggskala som inte var tydligt märkt som sådan, eller en graf med en loggskala som presenteras för en tittare som inte kände till logaritmiska skalor, skulle i allmänhet resultera i en representation som fick datavärden att se av liknande storlek, faktiskt, vara av vitt skilda storleksordningar. Felanvändning av en log-skala kan göra att väldigt olika värden (som 10 och 10 000) visas tätt intill varandra (på en bas-10 log-skala skulle de bara vara 1 och 4). Eller det kan få små värden att verka negativa på grund av hur logaritmiska skalor representerar tal som är mindre än basen.
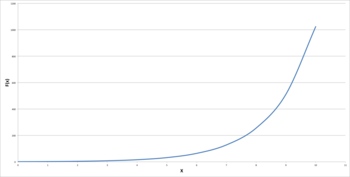
Missbruk av logga skalor kan också göra att relationer mellan kvantiteter verkar linjära medan dessa relationer är exponentiella eller maktlagar som stiger mycket snabbt mot högre värden. Det har konstaterats, om än huvudsakligen på ett humoristiskt sätt, att "allt som helst ser linjärt ut på en log-logg plot med tjock tusch" .
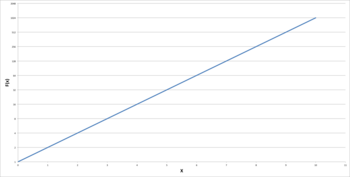
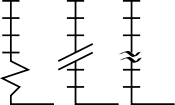
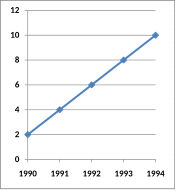
Båda graferna visar en identisk exponentialfunktion av f ( x ) = 2 x . Grafen till vänster använder en linjär skala som tydligt visar en exponentiell trend. Grafen till höger använder dock en logaritmisk skala, som genererar en rät linje. Om grafvisaren inte var medveten om detta, skulle grafen tyckas visa en linjär trend.
Trunkerad graf
En trunkerad graf (även känd som en trasad graf ) har en y- axel som inte börjar på 0. Dessa grafer kan skapa intryck av en viktig förändring där det är relativt liten förändring.
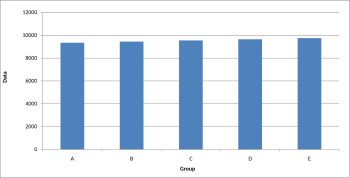
Även om trunkerade grafer kan användas för att övertrassera skillnader eller för att spara utrymme, avråds användningen av dem ofta. Kommersiell programvara som MS Excel tenderar att trunkera grafer som standard om alla värden ligger inom ett smalt intervall, som i det här exemplet. För att visa relativa skillnader i värden över tid kan ett indexdiagram användas. Trunkerade diagram kommer alltid att förvränga de underliggande siffrorna visuellt. Flera studier fann att även om människor var korrekt informerade om att y-axeln var trunkerad, överskattade de fortfarande de faktiska skillnaderna, ofta avsevärt.
Dessa grafer visar identiska data ; men i det trunkerade stapeldiagrammet till vänster verkar data visa signifikanta skillnader, medan dessa skillnader knappast är synliga i det vanliga stapeldiagrammet till höger.
Det finns flera sätt att indikera y -axelbrytningar:
Axeländringar
Att ändra y -axelns maximum påverkar hur grafen ser ut. Ett högre maximum gör att grafen verkar ha mindre volatilitet, mindre tillväxt och en mindre brant linje än ett lägre maximum.
Ändra förhållandet av grafens dimensioner Originalgraf Halvbredd, dubbelt så hög Två gånger bredd, halvhöjd 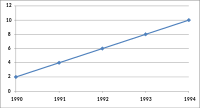

Att ändra förhållandet mellan en grafs dimensioner påverkar hur grafen ser ut.
Ingen skala
Skalorna i en graf används ofta för att överdriva eller minimera skillnader.
Missvisande stapeldiagram utan skala Mindre skillnad Mer skillnad
Avsaknaden av ett startvärde för y- axeln gör det oklart om grafen är trunkerad. Dessutom hindrar avsaknaden av bockmarker läsaren från att avgöra om grafstaplarna är korrekt skalade. Utan en skala kan den visuella skillnaden mellan staplarna enkelt manipuleras.
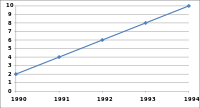
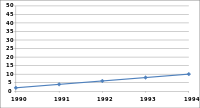
Även om alla tre graferna delar samma data, och därför den faktiska lutningen för ( x , y ) data är densamma, kan sättet som data plottas ändra det visuella utseendet på vinkeln som linjen på grafen gör. Detta beror på att varje plot har en annan skala på sin vertikala axel. Eftersom skalan inte visas kan dessa grafer vara missvisande.
Felaktiga intervaller eller enheter
De intervall och enheter som används i en graf kan manipuleras för att skapa eller mildra förändringsuttryck.
Utelämnar data
Grafer skapade med utelämnade data tar bort information från vilken man kan basera en slutsats.
I spridningsdiagrammet med saknade kategorier till vänster verkar tillväxten vara mer linjär med mindre variation.
I finansiella rapporter kan negativ avkastning eller data som inte korrelerar med en positiv utsikt uteslutas för att skapa ett mer gynnsamt visuellt intryck. [ citat behövs ]
3D
Användningen av en överflödig tredje dimension, som inte innehåller information, avråds starkt, eftersom det kan förvirra läsaren.
Komplexitet
Grafer är utformade för att möjliggöra enklare tolkning av statistiska data. Emellertid kan grafer med överdriven komplexitet fördunkla data och göra tolkningen svår.
Dålig konstruktion
Dåligt konstruerade grafer kan göra data svåra att urskilja och därmed tolka.
Extrapolering
Vilseledande grafer kan i sin tur användas för att extrapolera vilseledande trender.
Mäter distorsion
Flera metoder har utvecklats för att avgöra om grafer är förvrängda och för att kvantifiera denna förvrängning.
Lögnfaktor
var
En graf med en hög lie-faktor (>1) skulle överdriva förändringar i data den representerar, medan en med en liten lie-faktor (>0, <1) skulle dölja förändringar i data. En perfekt exakt graf skulle uppvisa en lögnfaktor på 1.
Diagramdiskrepansindex
var
Grafdiskrepansindex , även känt som grafförvrängningsindex ( GDI ), föreslogs ursprungligen av Paul John Steinbart 1998. GDI beräknas som en procentandel som sträcker sig från -100 % till positiv oändlighet, med noll procent som indikerar att grafen har varit korrekt konstruerad och allt utanför marginalen på ±5 % anses vara förvrängt. Forskning om användningen av GDI som ett mått på grafikförvrängning har funnit att det är inkonsekvent och diskontinuerligt, vilket gör det svårt att använda GDI som ett mått för jämförelser.
Data-bläck-förhållande
Data-bläckförhållandet bör vara relativt högt. Annars kan diagrammet ha onödig grafik.
Datatäthet
Datatätheten bör vara relativt hög, annars kan en tabell vara bättre lämpad för att visa data.
Användning i ekonomi och företagsrapporter
Grafer är användbara vid sammanfattning och tolkning av finansiella data. Grafer gör det möjligt att se trender i stora datamängder samtidigt som de tillåter att data tolkas av icke-specialister.
Grafer används ofta i företagens årsredovisningar som en form av intryckshantering . I USA behöver grafer inte granskas, eftersom de faller under AU Section 550 Annan information i dokument som innehåller reviderade finansiella rapporter .
Flera publicerade studier har tittat på användningen av grafer i företagsrapporter för olika företag i olika länder och har funnit frekvent användning av felaktig design, selektivitet och mätförvrängning i dessa rapporter. Förekomsten av vilseledande grafer i årsredovisningar har lett till krav på att standarder ska fastställas.
Forskning har funnit att även om läsare med dålig ekonomisk förståelse har en större chans att bli felinformerad av vilseledande grafer, kan även de med finansiell förståelse, såsom låneansvariga, bli vilseledda.
Akademin
Uppfattningen av grafer studeras inom psykofysik , kognitiv psykologi och beräkningsvisioner .
Se även
Böcker
- Huff, Darrell (1954). Hur man ljuger med statistik . bilder av Irving Geis (1:a upplagan). New York: Norton. ISBN 0393052648 .
- Hurley, Patrick J. (2000). En kortfattad introduktion till logik . Wadsworth Publishing. ISBN 9780534520069 .
- Keller, Gerald (2011). Statistik för företagsledning och ekonomi (förkortad, 9:e uppl.). Mason, OH: Sydvästra. ISBN 978-1111527327 .
- Kirk, Roger E. (2007). Statistik: En introduktion . Cengage Learning. ISBN 978-0-534-56478-0 . Hämtad 28 juni 2012 .
- Nolan, Susan; Heinzen, Thomas (2011). Statistik för beteendevetenskaperna . Macmillan. ISBN 978-1-4292-3265-4 . Hämtad 28 juni 2012 .
- Rumsey, Deborah (2010). Statistik Essentials for Dummies . John Wiley & Sons. ISBN 978-0-470-61839-4 . Hämtad 28 juni 2012 .
- Weiss, Neil A. (1993). Elementär statistik . Addison-Wesley. ISBN 978-0-201-56640-6 . Hämtad 28 juni 2012 .
- Tufte, Edward (1997). Visuella förklaringar: bilder och kvantiteter, bevis och berättelse . Cheshire, CT: Graphics Press. ISBN 978-0961392123 .
- Utts, Jessica M. (2005). Genomskinlig statistik (3:e upplagan). Belmont: Thomson, Brooks/Cole. ISBN 9780534394028 .
- Wainer, Howard (2000). Visuella uppenbarelser: Grafiska berättelser om öde och bedrägeri från Napoleon Bonaparte till Ross Perot . Psykologipress. ISBN 978-0-8058-3878-7 . Hämtad 19 juli 2012 .
- Whitbread, David (2001). Designmanualen (2:a upplagan). Sydney: University of New South Wales Press. ISBN 0868406589 .
Vidare läsning
- En diskussion om vilseledande grafer , Mark Harbison, Sacramento City College
- Robbins, Naomi B. (2005). Skapa mer effektiva grafer . Hoboken, NJ: Wiley-Interscience. ISBN 9780471698180 .
- Durbin CG, Jr (oktober 2004). "Effektiv användning av tabeller och figurer i abstracts, presentationer och papper". Andningsvård . 49 (10): 1233–7. PMID 15447809 .
- Goundar, Nadesa (2009). "Impression Management in Financial Reports Surrounding CEO Omsättning" (PDF) . Magisteravhandling . Unitec Institute of Technology. hdl : 10652/1250 . Hämtad 9 juli 2012 .
- Huff, Darrell; Geis, Irving (17 oktober 1993). Hur man ljuger med statistik . WW Norton & Company. ISBN 978-0-393-31072-6 . Hämtad 28 juni 2012 .
- Bracey, Gerald (2003). "Se genom grafer". Att förstå och använda utbildningsstatistik: det är enklare än du tror . Utbildningsforskningstjänst. ISBN 9781931762267 .
-
Harvey, J. Motulsky (juni 2009). "Användning och missbruk av logaritmiska axlar" (PDF) . GraphPad Software Inc. Arkiverad från originalet 2010-11-23.
{{ citera webben }}: CS1 underhåll: bot: ursprunglig URL-status okänd ( länk ) - Chandar, N.; Collier, D.; Miranti, P. (15 februari 2012). "Grafstandardisering och förvaltningsredovisning vid AT&T under 1920-talet". Bokföringshistorik . 17 (1): 35–62. doi : 10.1177/1032373211424889 . S2CID 155069927 .
- Mather, Paul; Ramsay, Alan; Steen, Adam (1 januari 2000). "Användningen och representationstroheten hos grafer i australiensiska IPO-prospekt" . Bokföring, revision och redovisningstidning . 13 (1): 65–83. doi : 10.1108/09513570010316144 . Arkiverad från originalet 2012-07-09.
- Beattie, Vivien; Jones, Michael John (1996). Finansiella diagram i företagens årsredovisningar: en genomgång av praxis i sex länder . London: Institute of Chartered Accountants i England och Wales. ISBN 9781853557071 .
- Galliat, Tobias (sommaren 2005). "Visualisierung von Informationsräumen" (PDF) . Fachhochschule Köln, Yrkeshögskolan Köln. Arkiverad från originalet (PDF) 2006-01-04 . Hämtad 9 juli 2012 .
- Carvalho, Clark R.; McMillan, Michael D. (september 1992). "Grafisk representation i ledningsbeslutsfattande: effekten av skalbrytning på den beroende axeln" ( PDF) . AIR FORCE INST OF TECH WRIGHT-PATTERSON AFB OH. Arkiverad (PDF) från originalet den 23 april 2019.
- Johnson, R. Rice; Roemmich, R. (oktober 1980). "Bilder som ljuger: missbruket av grafer i årsredovisningar". Management Accounting : 50–56.
- Davis, Alan J. (1 augusti 1999). "Dåliga grafer, bra lektioner" . ACM SIGGRAPH Datorgrafik . 33 (3): 35–38. doi : 10.1145/330572.330586 . S2CID 31491676 . Arkiverad från originalet 2000-03-05.
- Louwers, T.; Radtke, R; Pitman, M. (maj–juni 1999). "Please Pass the Salt: A Look at Creative Reporting in Annual Reports". Dagens CPA : 20–23.
- Beattie, Vivien; Jones, Michael John (maj 2001). "En jämförelse i sex länder av användningen av grafer i årsredovisningar". The International Journal of Accounting . 36 (2): 195–222. doi : 10.1016/S0020-7063(01)00094-2 .
- Wainer, Howard (1984). "Hur man visar data dåligt". Den amerikanska statistikern . 38 (2): 137–147. doi : 10.1080/00031305.1984.10483186 .
- Lane, David M.; Sándor, Anikó (1 januari 2009). "Designa bättre grafer genom att inkludera distributionsinformation och integrera ord, siffror och bilder" ( PDF) . Psykologiska metoder . 14 (3): 239–257. doi : 10.1037/a0016620 . PMID 19719360 .
- Campbell, Mary Pat (feb 2010). "Kalkylbladsproblem: fallgropar, bästa praxis och praktiska tips" . Forum för aktuariella praxis . Arkiverad från originalet 2019-04-23.
- Arocha, Carlos (maj 2011). "Ord eller grafer?" . Stepping Stone . Arkiverad från originalet 2019-04-23.
- Raschke, Robyn L.; Steinbart, Paul John (1 september 2008). "Att mildra effekterna av vilseledande grafer på beslut genom att utbilda användare om principerna för grafdesign". Journal of Information Systems . 22 (2): 23–52. doi : 10.2308/jis.2008.22.2.23 .