Littlewood–Richardson härskar

Inom matematik är Littlewood –Richardson-regeln en kombinatorisk beskrivning av de koefficienter som uppstår när man sönderdelar en produkt av två Schur-funktioner som en linjär kombination av andra Schur-funktioner. Dessa koefficienter är naturliga tal, som Littlewood–Richardson-regeln beskriver som att de räknar vissa sneda tablåer . De förekommer i många andra matematiska sammanhang, till exempel som mångfald i sönderdelningen av tensorprodukter av finita dimensionella representationer av allmänna linjära grupper, eller i sönderdelningen av vissa inducerade representationer i representationsteorin för den symmetriska gruppen , eller i området för algebraisk kombinatorik som handlar om unga tablåer och symmetriska polynom .

Littlewood–Richardson-koefficienter beror på tre partitioner , säg $\lambda ,\mu ,\nu$ , av vilka $\lambda$ och $\mu$ beskriver Schur-funktionerna som är multiplicerad, och $\nu$ ger Schur-funktionen vars koefficient är i den linjära kombinationen; med andra ord är de koefficienterna $c_{\lambda ,\mu }^{\nu }$ så att

$s_{\lambda }s_{\mu }=\summa _{\nu }c_{\lambda ,\mu }^{\nu }s_{\nu }.$

Littlewood–Richardson-regeln säger att $c_{\lambda ,\mu }^{\nu }$ är lika med antalet Littlewood-Richardson-tablåer med sned form $\nu /\lambda$ och vikten $\mu$ .

Historia

Tyvärr är Littlewood-Richardson-regeln mycket svårare att bevisa än vad man först misstänkte. Författaren fick en gång höra att Littlewood-Richardson-regeln hjälpte till att få män på månen men bevisades inte förrän efter att de kom dit.

Gordon James ( 1987 )

Littlewood–Richardson-regeln uttalades först av DE Littlewood och AR Richardson ( 1934 , sats III s. 119) men även om de hävdade det som ett sats bevisade de det bara i några ganska enkla specialfall. Robinson ( 1938 ) hävdade att han kompletterade sina bevis, men hans argument hade luckor, även om det var så dunkelt skrivet att dessa luckor inte märktes på en tid, och hans argument återges i boken (Littlewood 1950 ) . Några av luckorna fylldes senare av Macdonald (1995) . De första rigorösa bevisen för regeln gavs fyra decennier efter att den hittades, av Schützenberger ( 1977 ) och Thomas (1974) , efter att den nödvändiga kombinatoriska teorin utvecklats av C. Schensted ( 1961 ), Schützenberger ( 1963 ) och Knuth (1963 ) . 1970 ) i ​​deras arbete med Robinson–Schensted-korrespondensen . Det finns nu flera korta bevis på regeln, såsom ( Gasharov 1998 ) och ( Stembridge 2002 ) med Bender-Knuth-involutioner . Littelmann (1994) använde Littelmanns vägmodell för att generalisera Littlewood–Richardson-regeln till andra halvenkla Lie-grupper.

Littlewood-Richardson-regeln är ökänd för antalet fel som dök upp innan dess fullständiga, publicerade bevis. Flera publicerade försök att bevisa det är ofullständigt, och det är särskilt svårt att undvika fel när man gör handberäkningar med det: även det ursprungliga exemplet i DE Littlewood och AR Richardson (1934) innehåller ett fel.

Littlewood–Richardson tablåer

En tablå av Littlewood–Richardson

En Littlewood–Richardson-tablå är en skev semistandard-tablå med den ytterligare egenskapen att sekvensen som erhålls genom att sammanfoga dess omvända rader är ett gitterord (eller gitterpermutation), vilket betyder att i varje initial del av sekvensen vilket nummer som helst $i$ förekommer minst lika ofta som talet $i+1$ . En annan ekvivalent (men inte helt uppenbart så) karaktärisering är att tablån själv, och varje tablå som erhålls från den genom att ta bort ett antal av dess kolumner längst till vänster, har en svagt minskande vikt. Många andra kombinatoriska föreställningar har hittats som visar sig stämma överens med Littlewood–Richardson-tablåer och kan därför också användas för att definiera Littlewood–Richardson-koefficienterna.

Ännu en Littlewood–Richardson-tablå

Exempel

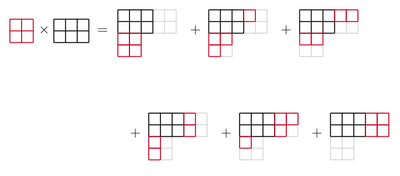
Betrakta fallet att $\lambda =(2,1)$ , $\mu =(3,2,1)$ och $\nu =(4,3,2)$ . Då kan det faktum att $c_{\lambda ,\mu }^{\nu }=2$ härledas från det faktum att de två tablåerna som visas till höger är de enda två Littlewood– Richardsons tablåer med formen $\nu /\lambda$ och vikten $\mu$ . Eftersom den sista rutan på den första icke-tomma raden i skevningsdiagrammet bara kan innehålla en post 1, måste hela den första raden fyllas med post 1 (detta är sant för alla Littlewood–Richardson-tablåer); i den sista rutan i den andra raden kan vi bara placera en 2:a genom kolumnstränghet och det faktum att vårt gitterord inte kan innehålla någon större post innan det innehåller en 2. För den första rutan i den andra raden kan vi nu antingen använda en 1:a eller en 2. När den posten väl är vald, måste den tredje raden innehålla de återstående posterna för att göra vikten (3,2,1), i en svagt ökande ordning, så vi har inget val kvar längre; i båda fallen visar det sig att vi hittar en Littlewood–Richardson-tablå.

En mer geometrisk beskrivning

Villkoret att sekvensen av poster som läses från tablån i en något märklig ordning från ett gitterord kan ersättas med ett mer lokalt och geometriskt tillstånd. Eftersom det i en semistandard tablå aldrig förekommer lika poster i samma kolumn, kan man numrera kopiorna av vilket värde som helst från höger till vänster, vilket är deras förekomstordning i sekvensen som ska vara ett gitterord. Kalla numret så associerat med varje post dess index, och skriv en post i med index j som i [ j ]. Om nu någon Littlewood–Richardson-tablå innehåller en post $i>1$ med index j , då bör den posten i [ j ] förekomma i en rad strikt under den för ${\ displaystyle (i-1)[j]}$ (vilket säkert också förekommer, eftersom posten i − 1 förekommer minst lika ofta som posten i gör). Faktum är att posten i [ j ] också bör förekomma i en kolumn inte längre till höger än samma post $(i-1)[j]$ (som vid första anblicken verkar vara vara ett strängare villkor). Om vikten av Littlewood-Richardson-tablån är fastställd i förväg, kan man bilda en fast samling av indexerade poster, och om dessa är placerade på ett sätt som respekterar de geometriska begränsningarna, utöver dem för halvstandardtablåer och villkoret som indexerade kopior av samma poster bör respektera höger-till-vänster-ordning av indexen, då är de resulterande tablåerna garanterat Littlewood–Richardson-tablåer.

En algoritmisk form av regeln

Littlewood–Richardson som nämnts ovan ger ett kombinatoriskt uttryck för individuella Littlewood–Richardson-koefficienter, men ger ingen indikation på en praktisk metod för att räkna upp Littlewood–Richardson-tablåerna för att hitta värdena för dessa koefficienter. För givna $\lambda ,\mu ,\nu$ finns det faktiskt inget enkelt kriterium för att avgöra om några Littlewood–Richardson-tablåer med formen $\nu /\lambda$ och av vikt $\mu$ existerar överhuvudtaget (även om det finns ett antal nödvändiga villkor, av vilka det enklaste är $|\lambda |+|\mu |= |\nu |$ ); därför verkar det oundvikligt att man i vissa fall måste gå igenom en noggrann sökning, bara för att finna att det inte finns några lösningar.

Icke desto mindre leder regeln till en ganska effektiv procedur för att bestämma den fullständiga nedbrytningen av en produkt av Schur-funktioner, med andra ord för att bestämma alla koefficienter ${\displaystyle c_{\lambda ,\mu }^{\nu$ för fasta λ och μ, men varierande ν. Detta fixerar vikten av Littlewood–Richardson-tablåerna som ska konstrueras och den "inre delen" λ av deras form, men lämnar den "yttre delen" ν fri. Eftersom vikten är känd är uppsättningen av indexerade poster i den geometriska beskrivningen fast. Nu för successiva indexerade poster kan alla möjliga positioner som tillåts av de geometriska begränsningarna prövas i en bakåtspårningssökning . Posterna kan prövas i stigande ordning, medan de bland lika poster kan prövas genom minskande index. Den senare punkten är nyckeln till effektiviteten av sökproceduren: posten i [ j ] är då begränsad till att vara i en kolumn till höger om ${\displaystyle i[j+1]} ,$ men nej längre till höger än $i-1[j]$ (om sådana poster finns). Detta begränsar kraftigt uppsättningen av möjliga positioner, men lämnar alltid minst en giltig position för $i[j]$ ; sålunda kommer varje placering av en post att ge upphov till minst en komplett Littlewood–Richardson-tablå, och sökträdet innehåller inga återvändsgränder.

En liknande metod kan användas för att hitta alla koefficienter $c_{\lambda ,\mu }^{\nu }$ för fasta λ och ν, men varierande μ.

Littlewood–Richardson-koefficienter

Littlewood–Richardson-koefficienterna c
^ν _λμ visas på följande sätt som är relaterade till varandra:

• De är strukturkonstanter för produkten i ringen av symmetriska funktioner med avseende på basen för Schur-funktioner

$s_{\lambda }s_{\mu }=\summa c_{\lambda \mu }^{\nu }s_{\nu }$

eller ekvivalent c
^ν _λμ är den inre produkten av s _ν och s _λ s _μ .

• De uttrycker skeva Schur-funktioner i termer av Schur-funktioner

$\lambda }=\sum _{\mu }c_{\lambda \mu }^{\nu }s_{\mu }.} C ν λμ visas$

• / som
  ^{skärningsnummer} _på en Grassmannan :

$\sigma _{\lambda }\sigma _{\mu }=\summa c_{\lambda \mu }^{\nu }\sigma _{\nu }$

där σ _μ är klassen av Schubert-varianten av en Grassmannian motsvarande μ .

• c
  ^ν _λμ är antalet gånger den irreducibla representationen V _λ ⊗ V _μ av produkten av symmetriska grupper S _{| λ |} × S _{| μ |} förekommer i begränsningen av representationen V _v av S _{| ν |} till S _{| λ |} × S _{| μ |} . Med Frobenius reciprocitet är detta också antalet gånger som V _ν förekommer i representationen av S _{| ν |} inducerad från V _λ ⊗ V _μ .
• c
  ^ν _λμ uppträder i sönderdelningen av tensorprodukten ( Fulton 1997 ) av två Schur-moduler (irreducerbara representationer av speciella linjära grupper )

$E^{\lambda }\otimes E^{\mu }=\bigoplus _{\nu }(E^{\nu})^{\oplus c_{\lambda \mu }^{\nu }} .$

• c
  ^ν _λμ är antalet standard Young-tablåer med formen ν / μ som är jeu de taquin ekvivalenta med någon fast standard Young-tablå med formen λ .
• c
  ^ν _λμ är antalet Littlewood–Richardson-tablåer med formen ν / λ och vikten μ .
• c
  ^ν _λμ är antalet bilder mellan μ och ν/λ.

Speciella fall

Pieris formel

Pieris formel , som är specialfallet med Littlewood–Richardson-regeln i fallet när en av partitionerna bara har en del , säger att

$S_{\mu }S_{n}=\summa _{\lambda }S_{\lambda }$

där S _n är Schur-funktionen för en partition med en rad och summan är över alla partitioner λ som erhålls från μ genom att lägga till n element till dess Ferrers-diagram , inga två i samma kolumn.

Rektangulära skiljeväggar

Om båda partitionerna är rektangulära till formen är summan också multiplicitetsfri ( Okada 1998 ). Fixa a , b , p och q positiva heltal med p $\geq$ q . Beteckna med $(a^{p})$ partitionen med p delar av längden a . Partitionerna som indexerar icke-triviala komponenter i ${\displaystyle s_{(a^{p})}s_{(b^{q})}} är$ dessa partitioner $\lambda$ med längden $\leq p+q$ så att

• $\lambda _{q+1}=\lambda _{q+2}=\cdots =\lambda _{p}=a,$
• $\lambda _{q}\geq \mathrm {max} (a,b)$
• $\lambda _{i}+\lambda _{p+q-i+1}=a+b,\quad {i=1,\dots ,q}.$

Till exempel,

.

Generaliseringar

Minskade Kronecker-koefficienter för den symmetriska gruppen

Den reducerade Kronecker-koefficienten för den symmetriska gruppen ${\bar {C}}_{\lambda ,\mu ,\nu }$ är en generalisering av $c_ {\lambda ,\mu }^{\nu }$ till tre godtyckliga Young-diagram $\lambda ,\mu ,\nu$ , vilket är symmetriskt under permutationer av de tre diagrammen.

Skew Schur-funktioner

Zelevinsky (1981) utökade Littlewood-Richardson-regeln till att snedvrida Schur-funktioner enligt följande:

$s_{\lambda }s_{\mu /\nu }=\summa _{\lambda +\ omega (T_{\geq j})\in P}s_{\lambda +\omega (T)}$

där summan är över alla tablåer T på μ/ν så att för alla j är sekvensen av heltal λ+ω( T _{≥ j} ) icke-ökande, och ω är vikten.

Newell-Littlewood-nummer

Newell-Littlewood-tal definieras från Littlewood-Richardson-koefficienter genom det kubiska uttrycket

$N_{\mu ,\nu ,\lambda }=\sum _{\alpha , \beta ,\gamma }c_{\alpha ,\beta }^{\mu }c_{\alpha ,\gamma }^{\nu }c_{\beta ,\gamma }^{\lambda }$

Newell-Littlewood-tal ger några av tensorproduktmultiplikheterna av finita dimensionella representationer av klassiska Lie-grupper av typerna $B,C,D$ .

Det icke-försvinnande villkoret på Young diagramstorlekar ${\displaystyle c_{\lambda ,\mu }^{\nu }\neq 0\implies |\lambda |+|\mu |=|\nu |} leder$ till

$N_{\mu ,\nu ,\lambda }\neq 0\implicerar \left\{{\begin{array}{l}|\lambda |-|\mu ||\leq |\ nu |\leq |\lambda |+|\mu |\\|\lambda |+|\mu |+|\nu |\in 2\mathbb {Z} \end{array}}\right.$

Newell-Littlewood-tal är generaliseringar av Littlewood-Richardson-koefficienter i den meningen att

$|\mu |+|\nu |=|\lambda |\implicerar N_{\mu ,\nu ,\lambda }=c_{\mu ,\ nu }^{\lambda }$

Newell-Littlewood-tal som involverar ett Young-diagram med endast en rad följer en regel av Pieri-typ: $N_{(k),\mu ,\nu }$ är antalet sätt att ta bort ${\frac {k+|\mu |-|\nu |}{2}}$ rutor från $\mu$ (från olika kolumner), lägg sedan till ${\frac {k-|\mu |+|\nu |}{2}}$ rutor (till olika kolumner) för att göra $\nu$ .

Newell-Littlewood-tal är strukturkonstanter för en associativ och kommutativ algebra vars grundelement är partitioner, med produkten $\mu \times \nu =\sum _{ \lambda }N_{\mu ,\nu,\lambda }\lambda$ . Till exempel,

$(1)\ gånger (k)=(k-1)+(k) +1)+(k,1)\quad {\text{(Newell–Littlewood)}}$

$(1)\ gånger (k)=(k+1)+(k,1)\quad {\text{(Littlewood–Richardson)}}$

Exempel

Exemplen på Littlewood–Richardson-koefficienter nedan ges i termer av produkter av Schur-polynomen S _π , indexerade med partitioner π, med hjälp av formeln

$S_{\lambda }S_{\mu }=\sum c_{\lambda \mu }^{\nu }S_{\nu }.$

Alla koefficienter med ν som mest 4 ges av:

• ₀₀ S S _π = S _π för vilken π som helst. där S =1 är Schur-polynomet för den tomma partitionen
• S ₁ S ₁ = S ₂ + S ₁₁
• S ₂ S ₁ = S ₃ + S ₂₁
• S ₁₁ S ₁ = S ₁₁₁ + S ₂₁
• S ₃ S ₁ = S ₄ + S ₃₁
• S ₂₁ S ₁ = S ₃₁ + S ₂₂ + S ₂₁₁
• S ₂ S ₂ = S ₄ + S ₃₁ + S ₂₂
• S ₂ S ₁₁ = S ₃₁ + S ₂₁₁
• S ₁₁₁ S ₁ = S ₁₁₁₁ + S ₂₁₁
• S ₁₁ S ₁₁ = S ₁₁₁₁ + S ₂₁₁ + S ₂₂

De flesta av koefficienterna för små partitioner är 0 eller 1, vilket i synnerhet händer när en av faktorerna har formen S _n eller S _11...1 , på grund av Pieris formel och dess transponerade motsvarighet. Det enklaste exemplet med en koefficient större än 1 händer när ingen av faktorerna har denna form:

• S ₂₁ S ₂₁ = S ₄₂ + S ₄₁₁ + S ₃₃ + 2 S ₃₂₁ + S ₃₁₁₁ + S ₂₂₂ + S ₂₂₁₁ .

För större partitioner blir koefficienterna mer komplicerade. Till exempel,

• S ₃₂₁ S ₃₂₁ = S ₆₄₂ + S ₆₄₁₁ + S ₆₃₃ +2 S ₆₃₂₁ + S ₆₃₁₁₁ + S ₆₂₂₂ + S ₆₂₂₁₁ + S ₅₅₂ + S ₅₅₁₁ +2 S ₅₄₃ +4 S ₅₄₂₁ +2 S 3 ₊ 54511 _{_} _ S ₅₃₂₂ +4 S ₅₃₂₁₁ + S ₅₃₁₁₁₁ +2 S ₅₂₂₂₁ + S ₅₂₂₁₁₁ + S ₄₄₄ +3 S ₄₄₃₁ +2 S ₄₄₂₂ +3 S _{44211 +} S 441111 +3 S ₄₃₃₂ +3 S ₄₃₃₄₁ +1 S _{43341 +1} S 42341 + S ₄₂₂₂₂ + S ₄₂₂₂₁₁ + S ₃₃₃₃ +2 S ₃₃₃₂₁ + S ₃₃₃₁₁₁ + S ₃₃₂₂₂ + S ₃₃₂₂₁₁ med 34 termer och total multiplicitet 62, och den största koefficienten är 4
• S ₄₃₂₁ S ₄₃₂₁ är en summa av 206 termer med den totala multipliciteten är 930, och den största koefficienten är 18.
• S ₅₄₃₂₁ S ₅₄₃₂₁ är en summa av 1433 termer med total multiplicitet 26704, och den största koefficienten (den för S _86543211 ) är 176.
• S ₆₅₄₃₂₁ S ₆₅₄₃₂₁ är en summa av 10873 termer med total multiplicitet är 1458444 (så att medelvärdet för koefficienterna är mer än 100, och de kan vara så stora som 2064).

Det ursprungliga exemplet som gavs av Littlewood & Richardson (1934 , s. 122-124) var (efter att ha korrigerat för 3 tablåer de hittade men glömde att inkludera i slutsumman)

• S ₄₃₁ S ₂₂₁ = S ₆₅₂ + S ₆₅₁₁ + S ₆₄₃ + 2 S ₆₄₂₁ + S ₆₄₁₁₁ + S ₆₃₃₁ + S ₆₃₂₂ + S ₆₃₂₁₁ + S ₅₅₃ + 2 S 5521 ₊ S 55111 ₊ 1 + 2 S ₃ + ₂ S 25 ₅₄₂₁₁ + S ₅₄₁₁₁₁ + S ₅₃₃₂ + S ₅₃₃₁₁ + 2 S _{53221 +} S ₅₃₂₁₁₁ + S ₄₄₃₂ + S _{44311 +} 2 S _{44221 +} S ₄₄₂₁₁₁ + S ₄₃₃₂₁ + S 4322 + S ₁₄₂₂ + S 4322

med 26 termer som kommer från följande 34 tablåer:

....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11 ...22 . ..22 ...2 ...2 ...2 ...2 ... ... ... .3 . .23 .2 .3 . .22 .2 .2 3 3 2 2 3 23 2 3 3 ....1 ....1 ....1 ....1 ....1 ....1 ....1 ....1 ....1 ....1 ...12 ...12 ...12 ...12 ...2 ...1 ...1 ...2 ...1 .23 .2 .3 . .13 .22 .2 .1 .2 3 2 2 2 3 23 23 2 3 3 ....1 ....1 ....1 ....1 ....1 ....1 ....1 ....1 ....1 ...2 ...2 ...2 ... ... ... ... ... .1 .3 . .12 .12 .1 .2 .2 2 1 1 23 2 22 13 1 3 2 2 3 3 2 2 3 3 .... .... .... .... .... ... .... .... ...1 ...1 ...1 ...1 ...1 ... ... ... .12 .12 .1 .2 .2 .11 .1 .1 23 2 22 13 1 22 12 12 3 3 2 2 3 23 2 3 3

Att beräkna skeva Schur-funktioner är liknande. Till exempel är de 15 Littlewood–Richardson-tablåerna för ν=5432 och λ=331

...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 .. .11 ...11 ...11 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 .11 .11 .11 .12 .11 .12 .13 .13 .23 .13 .13 .12 .12 .23 .23 12 13 22 12 23 13 12 24 14 14 22 23 33 13 34

   so S _5432/331 = Σ c
^ν _λμ S _μ = S ₅₂ + S ₅₁₁ + S ₄₁₁₁ + S ₂₂₂₁ + 2 S ₄₃ + 2 S ₃₂₁₁ + 2 S ₃₂₂ + 2 S ₃₃₁ + 3 S ₄₂₁ ( 9 Fulton , p. 64).

Anteckningar

•    Fulton, William (1997), Young tableaux , London Mathematical Society Student Texts, vol. 35, Cambridge University Press , sid. 121, ISBN 978-0-521-56144-0 , MR 1464693
•    Gasharov, Vesselin (1998), " A short proof of the Littlewood-Richardson rule" , European Journal of Combinatorics , 19 (4): 451–453, doi : 10.1006/eujc.1998.0212 , ISSN 0195-6690 5MR 430 5MR 430 ,
•   James, Gordon (1987), "The representation theory of the symmetric groups", The Arcata Conference on Representations of Finite Groups (Arcata, Calif., 1986) , Proc. Sympos. Pure Math., vol. 47, Providence, RI: American Mathematical Society , s. 111–126, MR 0933355
•    Knuth, Donald E. (1970), "Permutations, matrices, and generalized Young tableaux" , Pacific Journal of Mathematics , 34 (3): 709–727, doi : 10.2140 / pjm.1970.34.709 , ISSN 0030-8730 0272654
•   Littelmann, Peter (1994), "A Littlewood-Richardson rule for symmetrizable Kac-Moody algebras" (PDF) , Invent. Matematik. , 116 : 329–346, Bibcode : 1994InMat.116..329L , doi : 10.1007/BF01231564 , S2CID 85546837
•    Littlewood, Dudley E. (1950), Theory of group characters and matrix representations of groups , AMS Chelsea Publishing, Providence, RI, ISBN 978-0-8218-4067-2 , MR 0002127
•    Littlewood, DE; Richardson, AR (1934), "Group Characters and Algebra", Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character , The Royal Society, 233 (721–730): 99–141, Bibcode : 1934RSPTA.233 ... 99L , doi : 10.1098/rsta.1934.0015 4 , ISSN 924 JSTOR 91293
•    Macdonald, IG (1995), Symmetric functions and Hall polynomials , Oxford Mathematical Monographs (2nd ed.), The Clarendon Press Oxford University Press, ISBN 978-0-19-853489-1 , MR 1354144 , arkiverad från originalet den 2012- 12-11
•    Okada, Soichi (1998), "Applications of minor summation formulas to rectangular-shaped representations of classical groups", Journal of Algebra , 205 (2): 337–367, doi : 10.1006 / jabr.1997.7408 , ISSN 0321-86 1632816
•    Robinson, G. de B. (1938), "On the Representations of the Symmetric Group", American Journal of Mathematics , The Johns Hopkins University Press, 60 (3): 745–760, doi : 10.2307/2371609 , ISSN 0002- 9327 , JSTOR 2371609 Zbl 0019.25102
•    Schensted, C. (1961), "Longest growth and decreasing subsequences" , Canadian Journal of Mathematics , 13 : 179–191, doi : 10.4153/CJM-1961-015-3 , ISSN 0008-414X , 3MR 5012 ,
•   Schützenberger, MP (1963), "Quelques remarques sur une construction de Schensted", Mathematica Scandinavica , 12 : 117–128, doi : 10.7146/math.scand.a-10676 , ISSN 0025-5521 , 9001 701 , 9001  
•    Schützenberger, Marcel-Paul (1977), "La correspondance de Robinson" , Combinatoire et représentation du groupe symétrique (Actes Table Ronde CNRS, Univ. Louis-Pasteur Strasbourg, Strasbourg, 1976) , Lecture Notes in Mathematics, vol. 579, Berlin, New York: Springer-Verlag , s. 59–113 , doi : 10.1007/BFb0090012 , ISBN 978-3-540-08143-2 , MR 0498826
•    Stembridge, John R. (2002), "A concise proof of the Littlewood-Richardson rule" (PDF) , Electronic Journal of Combinatorics , 9 (1): Not 5, 4 s. (elektronisk), doi : 10.37236/1666 , ISSN 1077-8926 , MR 1912814
• Thomas, Glânffrwd P. (1974), Baxter algebras and Schur functions , Ph.D. Avhandling, Swansea: University College of Swansea
•   van Leeuwen, Marc AA (2001), "The Littlewood-Richardson rule, and related combinatorics" (PDF) , Interaction of combinatorics and representation theory , MSJ Mem., vol. 11, Tokyo: Matte. Soc. Japan, s. 95–145, MR 1862150
•    Zelevinsky, AV (1981), "A generalization of the Littlewood-Richardson rule and the Robinson-Schensted-Knuth correspondence", Journal of Algebra , 69 (1): 82–94, doi : 10.1016/0021-8693(81)90128 -9 , ISSN 0021-8693 , MR 0613858

externa länkar

• Ett onlineprogram som bryter ned produkter från Schur-funktioner med hjälp av Littlewood–Richardson-regeln