Lista över kvantlogiska grindar

I grindbaserad kvantberäkning används ofta olika uppsättningar av kvantlogiska grindar för att uttrycka kvantoperationer. Följande tabeller listar flera enhetliga kvantlogiska grindar, tillsammans med deras gemensamma namn, hur de representeras och några av deras egenskaper. Kontrollerade eller hermitiska konjugerade versioner av vissa av dessa grindar kanske inte är listade.

Identitetsport och global fas

namn	# qubits	Operatörssymbol	Matris	Kretsschema	Egenskaper	Refs
Identitet, no-op	1 (alla)	${\textstyle I,\;\mathbb {I} }$ , 𝟙	${\begin{bmatrix}1&0\\0&1\end{bmatrix}}$	eller	Hermitian Identitetselement
Global fas	1 (alla)	${\textstyle \mathrm {Ph} }$ , ${\textstyle \mathrm {Fas} }$ eller ${\textstyle \mathrm {e} ^{i\delta }I}$	$\mathrm {e} ^{i\delta }{\begin{bmatrix}1&0\\0&1\end{bmatrix}}$		Kontinuerliga parametrar: $\delta$ (period $2\pi$ ) Exponentiell form: $\exp(i\delta I)$

Identitetsporten är identitetsoperationen $I|\psi \rangle =|\psi \rangle$ , de flesta gångerna visas inte denna grind i kretsscheman, men den är användbar när man beskriver matematiska resultat.

Det har beskrivits som en "väntecykel" och en NOP .

Den globala fasgrinden introducerar en global fas $e^{i\varphi }$ till hela qubit-kvanttillståndet. Ett kvanttillstånd är unikt definierat upp till en fas. På grund av Born-regeln har en fasfaktor ingen effekt på ett mätresultat : $|e^{i\varphi }|=1$ för valfri $\varphi$ .

Eftersom $e^{i\delta }|\psi \rangle \otimes |\phi \rangle =e^{i\delta }(|\psi \rangle \otimes |\phi \rangle ),$ när den globala fasgrinden appliceras på en enda qubit i ett kvantregister ändras hela registrets globala fas.

Även $\mathrm {Ph} (0)=I.$

Dessa grindar kan utökas till valfritt antal qubits eller qudits .

Clifford qubit grindar

Den här tabellen innehåller vanliga Clifford-grindar för qubits.

Namn	# qubits	Operatörssymbol	Matris	Kretsschema	Vissa fastigheter	Refs
Pauli X , NOT, bit flip	1	${\textstil X,\;\mathrm {INTE} ,\;\sigma _{x}}$	${\begin{bmatrix}0&1\\1&0\end{bmatrix}}$	eller	Hermitian Pauli-gruppen Spårlöst Ofrivilligt
Pauli Y	1	${\textstil Y,\;\sigma _{y}}$	${\begin{bmatrix}0&-i\\i&0\end{bmatrix}}$		Hermitian Pauli-gruppen Spårlöst Ofrivilligt
Pauli Z , phase flip	1	${\textstil Z,\;\sigma _{z}}$	${\begin{bmatrix}1&0\\0&-1\end{bmatrix}}$		Hermitian Pauli-gruppen Spårlöst Ofrivilligt
Fasgrind S , kvadratroten ur Z	1	${\textstyle S,\;{\sqrt {Z}}}$	${\begin{bmatrix}1&0\\0&i\end{bmatrix}}$
Kvadratroten ur X , kvadratroten ur NOT	1	${\textstyle {\sqrt {X}}}$ , ${\textstyle V}$ , ${\textstyle {\sqrt {\mathrm {NOT} }},\;\mathrm {SX} }$	${\frac {1}{2}}{\begin{bmatrix}1+i&1-i\\1-i&1+i\end{ bmatrix}}$
Hadamard , Walsh-Hadamard	1	${\textstyle H}$	${\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}$		Hermitian Spårlöst Ofrivilligt
Controlled NOT , controlled- X , controlled-bit flip, reversibel exklusiv ELLER , Feynman	2	${\textstyle \mathrm {CNOT} }$ , ${\textstyle \mathrm {XOR} ,\;\mathrm {CX} }$	${\displaystyle {\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{bmatrix}}} [ 1 1 1 1 ] {\displaystyle {\begin{$${\begin{bmatrix}1&0&0&0\\0&0&0&1\\0&0&1&0\\0&1&0&0\end{bmatrix}}$		Hermitian Ofrivilligt Genomförande: Cirac–Zoller gate
Antikontrollerad-NOT, antikontrollerad- X , nollkontroll, kontroll-på-0-NOT, reversibel exklusiv NOR	2	${\textstyle {\overline {\mathrm {C} }}\mathrm {X} }$ , ${\textstil {\text{kontrollerad[0]-NOT}}}$ , ${\textstyle \mathrm {XNOR} }$	${\begin{bmatrix}0&1&0&0\\1&0&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}$		Hermitian Ofrivilligt
Kontrollerad- Z , kontrollerad skyltflip, kontrollerad fasvändning	2	${\textstyle \mathrm {CZ} }$ , ${\textstyle \mathrm {CPF} }$ , ${\textstyle \mathrm {CSIGN} }$ , ${\textstyle \ mathrm {CPHASE} }$	${\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&-1\end{bmatrix}}$		Hermitian Ofrivilligt Symmetrisk Genomförande: Duan-Kimble gate
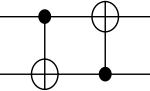
Dubbelstyrd NOT	2	${\textstyle \mathrm {DCNOT} }$	${\begin{bmatrix}1&0&0&0\\0&0&1&0\\0&0&0&1\\0&1&0&0\end{bmatrix}}$		Särskild enhetlig
Byta	2	${\textstyle \mathrm {SWAP} }$	${\begin{bmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\end{bmatrix}}$	eller	Hermitian Ofrivilligt Symmetrisk
Imaginärt byte	2	${\mbox{iSWAP}}$	${\begin{bmatrix}1&0&0&0\\0&0&i&0\\0&i&0&0\\0&0&0&1\end{bmatrix}}$	eller	Särskild enhetlig Symmetrisk
Fermionbyte	2	${\mbox{fSWAP}}$	${\begin{bmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&-1\end{bmatrix}}$		Särskild enhetlig Symmetrisk

Andra Clifford-portar, inklusive högre dimensionella sådana ingår inte här men kan per definition genereras med ${\textstyle H,S}$ och ${\textstyle \mathrm {CNOT} }$ .

Observera att om en Clifford-port A inte är i Pauli-gruppen, är ${\sqrt {A}}$ eller controlled- A inte i Clifford-gates.

Clifford-setet är inte ett universellt quantum gate-set.

Icke-Clifford qubit grindar

Relativa fasgrindar

Namn	# qubits	Operatörssymbol	Matris	Kretsschema	Egenskaper	Refs
Fasförskjutning	1	${\textstyle P(\varphi ),\;R(\varphi ),\;u_{1}(\varphi )}$	${\begin{bmatrix}1&0\\0&\mathrm {e} ^{i\varphi }\end{bmatrix}}$		Kontinuerliga parametrar: $\varphi$ (period $2\pi$ )
Fasgrind T, π/8-grind, fjärde roten av Z	1	${\textstyle T,P(\pi /4)}$ eller ${\textstyle {\sqrt[{4}]{Z}}}$	${\begin{bmatrix}1&0\\0&\mathrm {e} ^{i\pi /4}\end{bmatrix}}$
Kontrollerad fas	2	${\textstyle \mathrm {CPhase} (\varphi ),\mathrm {CR} (\varphi )}$	${\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&e^{i\varphi }\end{bmatrix}}$		Kontinuerliga parametrar: $\varphi$ (period $2\pi$ ) Symmetrisk
Kontrollerad fas S	2	$\mathrm {CS} ,{\text{kontrollerad-}}S$	${\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&i\end{bmatrix}}$		Symmetrisk

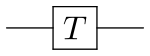
Fasskiftet är en familj av en-qubit-grindar som kartlägger bastillstånden $P(\varphi )|0\rangle =|0\rangle$ och $P(\varphi )|1\rangle =e^{i\varphi }|1\rangle$ . Sannolikheten att mäta en $|0\rangle$ eller $|1\rangle$ är oförändrad efter applicering av denna grind, men den modifierar fasen för kvanttillståndet. Detta motsvarar att spåra en horisontell cirkel (en latitudlinje), eller en rotation längs z-axeln på Bloch-sfären med $\varphi$ radianer. Ett vanligt exempel är T- porten där ${\textstyle \varphi ={\frac {\pi }{4}}}$ (historiskt känd som $\pi /8$ gate), fasgrinden. Observera att vissa Clifford-grindar är specialfall av fasskiftgrinden: $P(0)=I,\;P(\pi )=Z;P(\pi /2)=S.$

Argumentet till fasförskjutningsgrinden är i U(1) , och grinden utför en fasrotation i U(1) längs det specificerade bastillståndet (t.ex. $P(\varphi )$ roterar fasen ca. $|1\rangle$ ) . Att utöka $P(\varphi )$ till en rotation kring en generisk fas av båda bastillstånden i ett 2-nivås kvantsystem (en qubit ) kan göras med en seriekrets : $P(\beta )\cdot X\cdot P(\alpha )\cdot X={\begin{bmatrix} e^{i\alpha }&0\\0&e^{i\beta }\end{bmatrix}}$ . När $\alpha =-\beta$ är denna grind rotationsoperatorn $R_{z}(2\beta )$ gate och om $\alpha =\beta$ är det en global fas.

T - portens historiska namn på $\pi /8$ -porten kommer från identiteten ${\displaystyle R_{z}( \pi /4)\operatörsnamn {Ph} \left({\frac {\pi }{8}}\right)=P(\pi /4)} ,$ där $R_{z}(\pi /4)={\begin{bmatrix}e^{-i\pi /8}&0\\0&e^{i\pi /8}\end{bmatrix}}$ .

Godtyckliga enkel-qubit fasskiftgrindar $P(\varphi)$ är naturligt tillgängliga för transmon -kvantprocessorer genom timing av mikrovågsstyrpulser. Det kan förklaras i termer av byte av ram .

Som med vilken enskild qubit-grind som helst kan man bygga en kontrollerad version av fasskiftgrinden. Med avseende på beräkningsbasen är den 2-qubit-styrda fasskiftgrinden: skiftar fasen med $\varphi$ endast om den verkar på tillståndet $|11\rangle$ :

$|a,b\rangle \mapsto {\begin{cases}e^{i\varphi }|a,b\rangle &{\mbox{för }}a=b=1\\|a,b\ rangle &{\mbox{annars.}}\end{cases}}$

Den kontrollerade Z (eller CZ) grinden är specialfallet där $\varphi =\pi$ .

Den styrda -S- grinden är fallet när den kontrollerade- $P(\varphi )$ när $\varphi =\pi /2$ och är en vanlig grind.

Roterande operatörsgrindar

Ytterligare information: Bloch sfär § Rotationer och Rotationsoperator (kvantmekanik)

Namn	# qubits	Operatörssymbol	Exponentiell form	Matris	Kretsschema	Egenskaper	Refs
Rotation kring x -axeln	1	${\textstyle R_{x}(\theta )}$	$\exp(-iX\theta /2)$	${\begin{bmatrix}\cos(\theta /2 )&-i\sin(\theta /2)\\-i\sin(\theta /2)&\cos(\theta /2)\end{bmatrix}}$		Särskild enhetlig Kontinuerliga parametrar: $\theta$ (period $4\pi$ )
Rotation kring y-axeln	1	${\textstyle R_{y}(\theta )}$	$\exp(-iY\theta /2)$	${\begin{bmatrix}\cos(\theta /2)&- \sin(\theta /2)\\\sin(\theta /2)&\cos(\theta /2)\end{bmatrix}}$		Särskild enhetlig Kontinuerliga parametrar: $\theta$ (period $4\pi$ )
Rotation kring z-axeln	1	${\textstyle R_{z}(\theta )}$	$\exp(-iZ\theta /2)$	${\begin{bmatrix}\exp(-i\theta /2)&0\\0&\exp(i\theta /2 )\end{bmatrix}}$		Särskild enhetlig Kontinuerliga parametrar: $\theta$ (period $4\pi$ )

Rotationsoperatorn grindar $R_{x}(\theta ),R_{y}(\theta )$ och $R_{z$ är de analoga rotationsmatriserna i tre kartesiska axlar av SO(3) , axlarna på Bloch- sfärprojektionen.

Eftersom Pauli-matriser är relaterade till generatorn av rotationer, kan dessa rotationsoperatorer skrivas som matrisexponentialer med Pauli-matriser i argumentet. Vilken enhetlig matris som helst på $2\times 2$ i SU(2) kan skrivas som en produkt (dvs seriekrets) av tre rotationsgrindar eller mindre. Observera att för tvånivåsystem som qubits och spinorer har dessa rotationer en period på 4π . En rotation på 2π (360 grader) returnerar samma tillståndsvektor med en annan fas .

Vi har också $R_{b}(-\theta )=R_{b}(\theta )^{\dolk }$ och $R_{b}(0)=I$ för alla $b\in \{x,y,z\}.$

Rotationsmatriserna är relaterade till Pauli- $R_{x}(\pi )=-iX,R_{y}(\pi )=-iY,R_{z}(\pi )=-iZ.$

Det är möjligt att räkna ut den samverkande verkan av rotationer på Pauli-vektorn , nämligen rotation effektivt med dubbel vinkel a för att tillämpa Rodrigues rotationsformel :

$R_{n}(-a){\vec {\sigma }}R_{n}(a)=e^{i{\frac {a}{2}}\left({\hat {n} }\cdot {\vec {\sigma }}\right)}~{\vec {\sigma }}~e^{-i{\frac {a}{2}}\left({\hat {n}} \cdot {\vec {\sigma }}\right)}={\vec {\sigma }}\cos(a)+{\hat {n}}\times {\vec {\sigma }}~\sin( a)+{\hat {n}}~{\hat {n}}\cdot {\vec {\sigma }}~(1-\cos(a))~.$

Att ta prickprodukten av vilken enhetsvektor som helst med formeln ovan genererar uttrycket av vilken enskild qubit-grind som helst när den är placerad i angränsande rotationsgrindar. Till exempel kan det visas att $R_{y}(-\pi /2)XR_{y}(\pi /2)={\hat {x}}\cdot ({\hat {y}}\times {\vec {\sigma }})=Z$ . Med hjälp av antipendlingsrelationen har vi också $R_{y}(-\pi /2)XR_{y}(\pi /2)=XR_{y}(+\pi /2)R_{y}(\pi /2)=X (-iY)=Z$ .

Rotationsoperatörer har intressanta identiteter. Till exempel, $R_{y}(\pi /2)Z=H$ och $XR_{y}(\pi /2)=H.$ Med hjälp av antipendlingsrelationerna har vi också $ZR_{y}(-\pi /2)=H$ och $R_{y}(-\pi /2)X=H.$

Global fas- och fasförskjutning kan omvandlas till varandra med Z-rotationsoperatorn: $R_{z}(\gamma )\operatörsnamn {Ph} \left({\frac {\gamma }{2}}\right)=P(\gamma )$ .

X ${\displaystyle {\sqrt {X}}}-$ grinden representerar en rotation av π ${\sqrt { X}}=e^{i\pi /4}R_{x}(\pi /2)$ 2 kring x- axeln vid Bloch-sfären .

Liknande rotationsoperatorgrindar finns för SU(3) som använder Gell-Mann-matriser . De är rotationsoperatorerna som används med qutrits .

Två qubit interaktionsgrindar

Namn	# qubits	Operatörssymbol	Exponentiell form	Matris	Kretsschema	Egenskaper	Res
XX interaktion	2	$R_{xx}(\phi )$ , ${\text{XX}}(\phi )$	$\exp \left(-i{\frac {\phi }{2}}X\otimes X\right)$	${\begin{bmatrix}\cos \left({\frac {\phi }{2}}\right)&0&0&-i\sin \left({\frac {\phi }{ 2}}\right)\\0&\cos \left({\frac {\phi }{2}}\right)&-i\sin \left({\frac {\phi }{2}}\right) &0\\0&-i\sin \left({\frac {\phi }{2}}\right)&\cos \left({\frac {\phi}{2}}\right)&0\\-i \sin \left({\frac {\phi}{2}}\right)&0&0&\cos \left({\frac {\phi}{2}}\right)\\\end{bmatrix}}$		Särskild enhetlig Kontinuerliga parametrar: $\theta$ (period $4\pi$ ) Genomförande: Mølmer–Sørensen gate
YY interaktion	2	$R_{yy}(\phi )$ , ${\text{YY}}(\phi )$	$\exp \left(-i{\frac {\phi }{2}}Y\otimes Y\right)$	${\begin{bmatrix}\cos \left({\frac {\phi }{2}}\right)&0&0&i\sin \left({\frac {\phi }{2}}\ höger)\\0&\cos \left({\frac {\phi }{2}}\right)&-i\sin \left({\frac {\phi}{2}}\right)&0\\0& -i\sin \left({\frac {\phi}{2}}\right)&\cos \left({\frac {\phi}{2}}\right)&0\\i\sin \left( {\frac {\phi }{2}}\right)&0&0&\cos \left({\frac {\phi }{2}}\right)\\\end{bmatrix}}$		Särskild enhetlig Kontinuerliga parametrar: $\theta$ (period $4\pi$ ) Genomförande: Mølmer–Sørensen gate
ZZ interaktion	2	${\textstyle {\displaystyle R_{zz}(\phi )}}$ , ${\text{ZZ}}(\phi )$	${\displaystyle \exp \left(-i{\frac {\phi }{2}}Z\otimes Z\right)}$	${\begin{bmatrix}e^{-i\phi /2}&0&0&0\\0&e^{i \phi /2}&0&0\\0&0&e^{i\phi /2}&0\\0&0&0&0&e^{-i\phi /2}\\\end{bmatrix}}$		Särskild enhetlig Kontinuerliga parametrar: $\theta$ (period $4\pi$ )
XY, XX plus YY	2	${\textstyle {\displaystyle R_{xy}(\phi )}}$ , ${\text{XY}}(\phi )$	${\displaystyle \exp \left[-i{\frac {\phi }{4}}(X\otimes X+Y\otimes Y)\right]}$	${\begin{bmatrix}1&0&0&0\\0&\ cos(\phi /2)&-i\sin(\phi /2)&0\\0&-i\sin(\phi /2)&\cos(\phi /2)&0\\0&0&0&1\\\end{ bmatrix}}$		Särskild enhetlig Kontinuerliga parametrar: $\theta$ (period $4\pi$ )

Qubit-qubit Ising-kopplingen eller Heisenberg-interaktionsgrindarna R _xx , R _yy och R _zz är 2-qubit-grindar som implementeras inbyggt i vissa fångade-jonkvantdatorer , med användning av till exempel Mølmer–Sørensen-grindproceduren .

Observera att dessa grindar också kan uttryckas i sinusform, till exempel $R_{xx}(\phi )=\exp \left(-i{\frac {\phi}{2}}X\otimes X\right)=\cos \left({\frac {\phi} {2}}\right)I\otimes Ii\sin \left({\frac {\phi }{2}}\right)X\otimes X$ .

CNOT-grinden kan sönderdelas ytterligare som produkter av rotationsoperatorgrindar och exakt en enkel interaktionsgrind med två kvbitar, till exempel

${\mbox{CNOT}}=e^{-i{\frac {\pi }{4}}}R_{y_{1}}(-\pi /2)R_{x_{1}}( -\pi /2)R_{x_{2}}(-\pi /2)R_{xx}(\pi /2)R_{y_{1}}(\pi /2).$

SWAP-grinden kan konstrueras från andra grindar, till exempel genom att använda de två qubit-interaktionsgrindarna : ${ \displaystyle {\text{SWAP}}=e^{i{\frac {\pi }{4}}}R_{xx}(\pi /2)R_{yy}(\pi /2)R_{zz} (\pi /2)}$ .

Bytesportar som inte kommer från Clifford

Namn	# qubits	Operatörssymbol	Matris	Kretsschema	Egenskaper	Refs
Kvadratrotsbyte	2	${\sqrt {\mathrm {SWAP} }}$	${\begin{bmatrix}1&0&0&0\\0&{\frac {1 }{2}}(1+i)&{\frac {1}{2}}(1-i)&0\\0&{\frac {1}{2}}(1-i)&{\frac { 1}{2}}(1+i)&0\\0&0&0&1\\\end{bmatrix}}$
Kvadratrot imaginärt byte	2	${\sqrt {\mbox{iSWAP}}}$	${\begin{bmatrix}1&0&0&0\\0&{\frac {1}{\sqrt {2}}}&{\frac {i}{\sqrt { 2}}}&0\\0&{\frac {i}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}&0\\0&0&0&1\end{bmatrix}}$		Särskild enhetlig
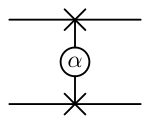
Swap (höjt till en makt)	2	${\mbox{SWAP}}^{\alpha }$	${\begin{bmatrix}1&0&0&0\\0&{\frac {1 +e^{i\pi \alpha }}{2}}&{\frac {1-e^{i\pi \alpha }}{2}}&0\\0&{\frac {1-e^{i \pi \alpha }}{2}}&{\frac {1+e^{i\pi \alpha }}{2}}&0\\0&0&0&1\end{bmatrix}}$		Kontinuerliga parametrar: $\alpha$ (period $2$ )
Fredkin , kontrollerat byte	3	$\mathrm {CSWAP}$ , $\mathrm {FREDKIN}$	$\displaystyle {\begin{bmatrix}1&0&0&0&0&0&0&0\\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0&0 &0&0&0&1&0\\0&0&0&0&0&1&0&0\\0&0&0&0&0&0&0&1\\\end{bmatrix}}}$	eller	Hermitian Ofrivilligt Funktionellt komplett reversibel gate för boolesk algebra

√ SWAP- grinden utför halvvägs av ett två-qubit-byte (se Clifford-grindar). Den är universell så att vilken många-qubit-grind som helst kan konstrueras av endast √ SWAP- och enstaka qubit-grindar. √ SWAP- grinden är dock inte maximalt intrasslande; mer än en tillämpning av det krävs för att producera ett Bell-tillstånd från produkttillstånd. √ SWAP- porten uppstår naturligt i system som utnyttjar utbytesinteraktion .

För system med Ising-liknande interaktioner är det ibland mer naturligt att introducera den imaginära swap eller iSWAP. Observera att $i{\mbox{SWAP}}=R_{xx}(-\pi /2)R_{yy} (-\pi /2)$ och ${\displaystyle {\sqrt {i{\mbox{SWAP}}}}=R_{xx}(-\pi /4)R_{yy}(-\pi /4)} eller$ mer i allmänhet ${\sqrt[{n}]{i{\mbox{SWAP}}}}=R_{ xx}(-\pi /2n)R_{yy}(-\pi /2n)$ för alla reella n utom 0.

SWAP ^α uppstår naturligt i spintroniska kvantdatorer.

Fredkin gate (även CSWAP eller CS gate), uppkallad efter Edward Fredkin , är en 3-bitars gate som utför ett kontrollerat swap . Det är universellt för klassisk beräkning. Den har den användbara egenskapen att siffrorna 0:or och 1:or bevaras genomgående, vilket i biljardbollsmodellen innebär att samma antal bollar matas ut som indata.

Andra namngivna portar

Namn	# qubits	Operatörssymbol	Matris	Kretsschema	Egenskaper	Döpt efter	Refs
Generell enkel qubit rotation	1	$U(\theta ,\phi ,\lambda )$	${\begin{bmatrix}\cos(\theta /2)&-e^{-i\lambda }\sin(\theta /2)\\e^{-i\phi}\sin(\theta /2)&e^{i(\lambda +\phi )}\cos(\theta /2)\end{bmatrix}}$		Implementerar en godtycklig en-qubit-rotation Kontinuerliga parametrar: $\theta ,\phi ,\lambda$ (period $2\pi$ )	Öppna QASM U-porten
Barenco	2	$\mathrm {BARENCO} (\alpha ,\phi ,\theta )$	${\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&e^{i\alpha }\cos \theta &-\mathrm {i} e^{\mathrm {i} (\alpha -\phi )}\ sin \theta \\0&0&-\mathrm {i} e^{\mathrm {i} (\alpha +\phi )}\sin \theta &e^{i\alpha }\cos \theta \end{bmatrix}}$		Implementerar en kontrollerad godtycklig qubit-rotation Universal quantum gate Kontinuerliga parametrar: $\alpha ,\phi ,\theta$ (period $2\pi$ )	Adriano Barenco
Berkeley B	2	$B$	${\begin{bmatrix}\cos(\pi /8)&0&0&i\sin(\pi /8)\\0&\cos(3\pi /8) &i\sin(3\pi /8)&0\\0&i\sin(\pi /8)&\cos(\pi /8)&0\\i\sin(\pi /8)&0&0&\cos(\pi / 8)\\\end{bmatrix}}$		Särskild enhetlig Exponentiell form: $\exp \left[i{\frac {\pi }{8}}(2X\ibland X+Y\ibland Y)\right ]$	University of California Berkeley
Kontrollerad-V, kontrollerad kvadratrot INTE	2	$\mathrm {CSX} ,{\text{controlled-}}{\sqrt {X}},$${\text{controlled-}}V$	${\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&e^{i\pi /4} &e^{-i\pi /4}\\0&0&e^{-i\pi /4}&e^{i\pi /4}\end{bmatrix}}$
Core intrassling, kanonisk nedbrytning	2	$N(a,b,c)$ , $\mathrm {can} (a,b,c)$	${\begin{bmatrix}e^{ic}\cos(ab)&0&0&ie^{ic}\sin(ab)\\0&e^{-ic}\cos(a+b)&ie^{-ic} \sin(a+b)&0\\0&ie^{-ic}\sin(a+b)&e^{-ic}\cos(a+b)&0\\ie^{ic}\sin(ab)&0&0&e ^{ic}\cos(ab)\\\end{bmatrix}}$		Särskild enhetlig Universal quantum gate Exponentiell form $\exp \left[i(aX\otimes X+bY\otimes Y+cZ\otimes Z)\right]$ Kontinuerliga parametrar: $a,b,c$ (period $2\pi$ )
Dagwood Bumstead	2	${\text{DB}}$	${\begin{bmatrix}1&0&0&0\\0&\cos(3\pi /8)&-i\sin(3\pi /8)&0\\0&-i\sin(3\pi /8)& \cos(3\pi /8)&0\\0&0&0&1\\\end{bmatrix}}$		Särskild enhetlig Exponentiell form: $\exp \left[-i{\frac {3\pi }{16}}(X\otillfällen X+Y\o gånger Y )\höger]$	Serietidning Dagwood Bumstead
Ekade korsresonans	2	${\text{ECR}}$	${\frac {1}{\sqrt {2}}}{\begin{bmatrix}0&0&1&i\\0&0&i&1\\1&-i&0&0\\-i&1&0&0 \\\end{bmatrix}}$		Särskild enhetlig
Fermionisk simulering	2	$U_{\text{fSim}}(\theta ,\phi )$ , ${\text{fSim}}(\theta ,\phi )$	${\begin{bmatrix}1&0&0&0\\0&\cos(\theta)& -i\sin(\theta )&0\\0&-i\sin(\theta )&\cos(\theta )&0\\0&0&0&e^{i\phi }\\\end{bmatrix}}$		Särskild enhetlig Kontinuerliga parametrar: $\theta ,\phi$ (period $2\pi$ )
Givens	2	$G(\theta )$ , ${\text{Givens}}(\theta )$	${\begin{bmatrix}1&0&0&0\\0&\cos(\theta )&-\sin(\ theta )&0\\0&\sin(\theta )&\cos(\theta )&0\\0&0&0&1\\\end{bmatrix}}$		Särskild enhetlig Exponentiell form: $\exp \left[-i{\frac {\theta }{2}}(Y\otimes XX\otimes Y)\right]$ Kontinuerliga parametrar: $\theta ,\phi$ (period $2\pi$ )	Ger rotationer
Magi	2	${\mathcal {M}}$	${\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&i&0&0\\0&0&i&1\\0&0&i&-1\\1&- i&0&0\\\end{bmatrix}}$
Platan	2	${\text{syc}}$ , ${\text{fSim}}(\pi /2,\pi /6)$	${\begin{bmatrix}1&0&0&0\\0&0&-i&0\\0&-i&0&0\\0&0&0&\mathrm {e} ^{-i\pi /6} \end{bmatrix}}$			Googles Sycamore -processor
Deutsch	3	$D_{\theta }$ , $D(\theta )$	${\begin{bmatrix}1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\\0&0&0&1&0&0&0&0\\0&0&0&0&0&1&0&0&0&0&0&0&0&1&0&0&0&0&0 &0&0&i\cos \theta &\sin \theta \\0&0&0&0&0&0&\sin \theta &i\cos \theta \ \\end{bmatrix}}$		Kontinuerliga parametrar: $\theta ,\phi$ (period $2\pi$ ) Universal quantum gate	David Deutsch
Margolus, förenklat Toffoli	3	$M$ , ${\text{RCCX}}$	${\begin{bmatrix}1&0&0&0&0&0&0&0\\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0&0&0&0&0&0&0&0 &0&0&0&-1&0&0\\0&0&0&0&0&0&0&1\\0&0&0&0&0&0&1&0\\\end{bmatrix }}$		Hermitian Ofrivilligt Särskild enhetlig Funktionellt komplett reversibel gate för boolesk algebra	Norman Margolus
Peres	3	$\mathrm {PG}$ , $\mathrm {Peres}$	$0&0&0&0&1&0&0&0\\0&0&0&0&0&1&0&0\\\end{bmatrix$		Funktionellt komplett reversibel gate för boolesk algebra	Asher Peres
Toffoli , kontrollerat-kontrollerat INTE	3	$\mathrm {CCNOT} ,\mathrm {CCX} ,\mathrm {Toff}$	$\displaystyle {\begin{bmatrix}1&0&0&0&0&0&0&0\\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0&0 &0&0&1&0&0\\0&0&0&0&0&0&0&1\\0&0&0&0&0&0&0&1&0\\\end{bmatrix}}}$		Hermitian Ofrivilligt Funktionellt komplett reversibel gate för boolesk algebra	Tommaso Toffoli