Konstant kärve

I matematik är den konstanta bunten på ett topologiskt utrymme $X$ associerad med en mängd $A$ en bunt av mängder på $X$ vars stjälkar alla är lika med $A$ . Det betecknas med ${\underline {A}}$ eller $A_{X}$ . Den konstanta preheafen med värdet $A$ är preheafen som tilldelar varje icke-tom öppen delmängd av $X$ värdet $A$ och vars alla restriktionskartor är identitetskartan $A\to A$ . Den konstanta skarven som är associerad med $A$ är skarvningen av den konstanta strängen som är associerad med $A$ . Denna bunt identifierar med bunten av lokalt konstanta $A$ -värderade funktioner på $X$ .

I vissa fall kan uppsättningen $A$ ersättas med ett objekt $A$ i någon kategori ${\textbf {C}}$ (t.ex. när ${\textbf { C}}$ är kategorin av abelska grupper , eller kommutativa ringar ).

Konstanta kärvar av abelska grupper förekommer särskilt som koefficienter i kärvkohomologi .

Grunderna

Låt $X$ vara ett topologiskt rum och $A$ en mängd. Sektionerna av den konstanta bunten ${\underline {A}}$ över en öppen uppsättning $U$ kan tolkas som de kontinuerliga funktionerna $U\to A$ , där $A$ ges den diskreta topologin . Om $U$ är ansluten är dessa lokalt konstanta funktioner konstanta. Om $f:X\to \{{\text{pt}}\}$ är den unika kartan till enpunktsutrymmet och $A$ betraktas som en kärve på $\{{\text{pt}}\}$ , då är den omvända bilden $f^{-1}A$ den konstanta bunten ${\ understryka {A}}$ på $X$ . Skarvutrymmet för ${\underline {A}}$ är projektionskartan A $\displaystyle A}$ (där $X\ gånger A\till X$ ges den diskreta topologin ).

Ett detaljerat exempel

Konstant förkärv på ett diskret tvåpunktsutrymme

Tvåpunkts diskret topologiskt utrymme

Låt $X$ vara det topologiska rummet som består av två punkter $p$ och $q$ med den diskreta topologin . $X$ har fyra öppna uppsättningar: $\varnothing ,\{p\},\{q\},\{p,q\ }$ . De fem icke-triviala inkluderingarna av de öppna uppsättningarna av $X$ visas i diagrammet.

En förlist på $X$ väljer en uppsättning för var och en av de fyra öppna uppsättningarna av $X$ och en restriktionskarta för var och en av de nio inneslutningarna (fem icke-triviala inneslutningar och fyra triviala). Den konstanta presheafen med värdet ${\displaystyle {\textbf {Z}}} ,$ som vi kommer att beteckna $F$ , är preheafen som väljer att alla fyra uppsättningarna ska vara ${\textbf {Z}}$ , heltal och alla begränsningskartor för att vara identiteten. $F$ är en funktor, därav en presheaf, eftersom den är konstant. $F$ uppfyller limningsaxiomet, men det är inte ett kärve eftersom det misslyckas med det lokala identitetsaxiomet på den tomma uppsättningen. Detta beror på att den tomma uppsättningen täcks av den tomma familjen av uppsättningar: Vacuously, två sektioner av $F$ över den tomma uppsättningen är lika när de är begränsade till någon uppsättning i den tomma familjen. Axiomet för den lokala identiteten skulle därför innebära att alla två sektioner av $F$ över den tomma mängden är lika, men detta är inte sant.

En liknande presheaf $G$ som uppfyller det lokala identitetsaxiomet över den tomma uppsättningen är konstruerad enligt följande. Låt $G(\varnothing )=0$ , där 0 är en enelementsmängd. På alla icke-tomma uppsättningar, ge $G$ värdet ${\textbf {Z}}$ . För varje inkludering av öppna uppsättningar $G$ antingen den unika kartan till 0, om den mindre uppsättningen är tom, eller identitetskartan på ${\textbf {Z}}$ .

Mellansteg för konstantkärven

Lägg märke till att som en konsekvens av det lokala identitetsaxiomet för den tomma uppsättningen är alla restriktionskartor som involverar den tomma uppsättningen tråkiga. Detta är sant för alla förkärva som uppfyller det lokala identitetsaxiomet för den tomma uppsättningen, och i synnerhet för alla kärve.

$G$ är en separerad presheaf (det vill säga uppfyller det lokala identitetsaxiomet), men till skillnad från $F$ misslyckas det med limningsaxiomet. $\{p,q\}$ täcks av de två öppna uppsättningarna $\{p\}$ och $\{q\}$ , och dessa uppsättningar har tom skärningspunkt. Ett avsnitt på $\{p\}$ eller på $\{q\}$ är ett element i ${\displaystyle {\textbf {Z}}} ,$ det vill säga det är ett nummer. Välj ett avsnitt $m$ över $\{p\}$ och $n$ över $\{q\}$ , och antag att ${ \displaystyle m\neq n}$ . Eftersom $m$ och $n$ begränsar till samma element 0 över $\varnothing$ , kräver limningsaxiomet att det finns en unik sektion $s$ på $G(\{p,q\})$ som begränsar till $m$ på $\{p\}$ och $n$ på $\{q\}$ . Men eftersom begränsningskartan från $\{p,q\}$ till $\{p\}$ är identiteten, $s=m$ , och på liknande sätt $s=n$ , så $m=n$ , en motsägelse.

Konstant kärve på ett tvåpunkts topologiskt utrymme

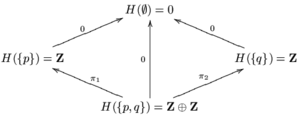
$G(\{p,q\})$ är för liten för att ge information om både $\{p\}$ och $\ {q\}$ . För att förstora den så att den uppfyller limningsaxiomet, låt $H(\{p,q\})=\mathbf {Z} \oplus \mathbf {Z}$ . Låt $\pi _{1}$ och $\pi _{2}$ vara de två projektionskartorna $\mathbf {Z} \oplus \mathbf {Z } \to \mathbf {Z}$ . Definiera $H(\{p\})={\text{im}}(\pi _{1})=\mathbf {Z}$ och $H(\{q\})={\text{im}}(\pi _{2})=\mathbf {Z}$ . För de återstående öppna uppsättningarna och inneslutningarna, låt $H$ lika med $G$ . $H$ är en bunt som kallas konstant kärv på $X$ med värdet ${\textbf {Z}}$ . Eftersom ${\textbf {Z}}$ är en ring och alla restriktionskartor är ringhomomorfismer, är $H$ en bunt av kommutativa ringar.

Se även

• Lokalt konstant kärve

• Avsnitt II.1 av    Hartshorne, Robin (1977), Algebraic Geometry , Graduate Texts in Mathematics , vol. 52, New York: Springer-Verlag, ISBN 978-0-387-90244-9 , MR 0463157
• Avsnitt 2.4.6 i   Tennison, BR (1975), Sheaf theory , ISBN 978-0-521-20784-3