Kelvin–Voigt material

Ett Kelvin-Voigt-material , även kallat ett Voigt-material , är det enklaste modellen viskoelastiska material som visar typiska gummiliknande egenskaper. Det är rent elastiskt på långa tidsskalor (långsam deformation), men visar ytterligare motstånd mot snabb deformation. Den är uppkallad efter den brittiske fysikern och ingenjören Lord Kelvin och den tyske fysikern Woldemar Voigt .

Definition

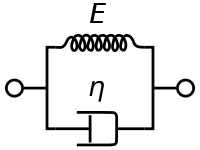
Kelvin-Voigt-modellen, även kallad Voigt-modellen, representeras av en rent viskös dämpare och en rent elastisk fjäder som är parallellkopplad som bilden visar.

Schematisk representation av Kelvin–Voigt-modellen.

Om vi istället kopplar dessa två element i serie får vi en modell av ett Maxwell-material .

Eftersom de två komponenterna i modellen är anordnade parallellt, är töjningarna i varje komponent identiska:

\varepsilon _{\text{Totalt}}=\varepsilon _{S}=\varepsilon _{D}.

där underskriften D indikerar spänningstöjningen i spjället och underskriften S indikerar spänningstöjningen i fjädern. På samma sätt kommer den totala spänningen att vara summan av spänningen i varje komponent:

\sigma _{\text{Totalt}}=\sigma _{S}+\sigma _{D}.

Från dessa ekvationer får vi att i ett Kelvin-Voigt-material styrs spänningen σ, töjningen ε och deras förändringshastighet med avseende på tiden t av ekvationer av formen:

\sigma (t)=E\varepsilon (t)+\eta {\frac {d\varepsilon (t)}{ dt}},

eller, i punktnotation:

\sigma =E\varepsilon +\eta {\dot {\varepsilon }},

där E är en elasticitetsmodul och $\eta$ är viskositeten . Ekvationen kan tillämpas antingen på skjuvspänningen eller normalspänningen hos ett material.

Effekt av en plötslig stress

Om vi plötsligt applicerar någon konstant spänning $\sigma _{0}$ på Kelvin-Voigt-material, så skulle deformationerna närma sig deformationen för det rena elastiska materialet $\sigma _{0}/E$ med skillnaden avtagande exponentiellt:

\varepsilon (t)={\frac {\sigma _{0}}{E}}(1-e^{-t /\tau _{R}}),

där t är tid och $\tau _{R}={\frac {\eta }{E}}$ är retardationstiden .

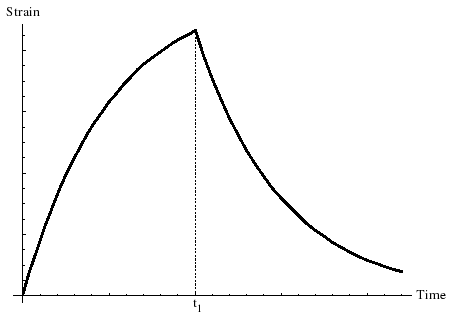
Om vi skulle frigöra materialet vid tidpunkten $t_{1}$ , då skulle det elastiska elementet fördröja materialet tillbaka tills deformationen blir noll. Fördröjningen följer följande ekvation:

\varepsilon (t>t_{1})=\varepsilon (t_{1})e^{-(t-t_{1})/\tau _{R}}.

Bilden visar beroendet av den dimensionslösa deformationen ${\frac {E\varepsilon (t)}{\sigma _{0}}}$ av dimensionslös tid $t /\tau _{R}$ . På bilden belastas spänningen på materialet vid tidpunkten $t=0$ , och släpps vid den senare dimensionslösa tiden $t_{1}^{*}= t_{1}/\tau _{R}$ .

Beroende av dimensionslös deformation av dimensionslös tid under konstant stress

Eftersom all deformation är reversibel (men inte plötsligt) är Kelvin–Voigt-materialet ett fast material .

Voigt-modellen förutsäger krypning mer realistiskt än Maxwell-modellen, för i den oändliga tidsgränsen närmar sig töjningen en konstant:

\lim _{t\to \infty }\varepsilon ={\frac {\sigma _{0}}{E}},

medan en Maxwell-modell förutsäger ett linjärt samband mellan belastning och tid, vilket oftast inte är fallet. Även om Kelvin-Voigt-modellen är effektiv för att förutsäga krypning är den inte bra på att beskriva avslappningsbeteendet efter att stressbelastningen tagits bort.

Dynamisk modul

Den komplexa dynamiska modulen för Kelvin-Voigt-materialet ges av:

E^{\star }(\omega )=E+i\eta \omega .

Således är de verkliga och imaginära komponenterna i den dynamiska modulen:

E_{1}=\Re [E(\omega )]=E,

E_{2}=\Im [E(\omega )]=\eta \omega .

Observera att $E_{1}$ är konstant, medan $E_{2}$ är direkt proportionell mot frekvensen (där den skenbara viskositeten, $\eta$ , är proportionalitetskonstanten ).

Meyers och Chawla (1999): Avsnitt 13.11 av Mechanical Behaviours of Materials, Mechanical behavior of Materials , 570–580. Prentice Hall, Inc.
http://stellar.mit.edu/S/course/3/fa06/3.032/index.html

Se även