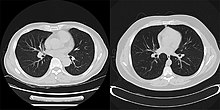
Iterativ rekonstruktion

Exempel som visar skillnader mellan filtrerad bakprojektion (höger halva) och iterativ rekonstruktionsmetod (vänster halva)

Iterativ rekonstruktion avser iterativa algoritmer som används för att rekonstruera 2D- och 3D-bilder i vissa bildtekniker . Till exempel, i datortomografi måste en bild rekonstrueras från projektioner av ett objekt. Här är iterativa rekonstruktionstekniker vanligtvis ett bättre, men beräkningsmässigt dyrare alternativ till den vanliga filtrerade bakprojektionsmetoden (FBP), som direkt beräknar bilden i ett enda rekonstruktionssteg. I nyare forskningsarbeten har forskare visat att extremt snabba beräkningar och massiv parallellism är möjlig för iterativ rekonstruktion, vilket gör iterativ rekonstruktion praktisk för kommersialisering.

Grundläggande koncept

CT-skanning med iterativ rekonstruktion (vänster) kontra filtrerad bakprojektion (höger)

Rekonstruktionen av en bild från den inhämtade datan är ett omvänt problem . Ofta är det inte möjligt att exakt lösa det omvända problemet direkt. I det här fallet måste en direkt algoritm approximera lösningen, vilket kan orsaka synliga rekonstruktionsartefakter i bilden. Iterativa algoritmer närmar sig den korrekta lösningen med hjälp av flera iterationssteg, vilket gör det möjligt att få en bättre rekonstruktion till priset av en längre beräkningstid.

Det finns ett stort utbud av algoritmer, men var och en börjar med en antagen bild, beräknar projektioner från bilden, jämför originalprojektionsdata och uppdaterar bilden baserat på skillnaden mellan de beräknade och de faktiska projektionerna.

Algebraisk rekonstruktion

Huvudartikel: Algebraisk rekonstruktionsteknik

Den algebraiska rekonstruktionstekniken (ART) var den första iterativa rekonstruktionstekniken som användes för datortomografi av Hounsfield .

iterativ gles asymptotisk minimumvarians

Huvudartikel: SAMV (algoritm)

Den iterativa Sparse Asymptotic Minimum Variance- algoritmen är en iterativ, parameterfri tomografisk rekonstruktionsmetod med superupplösning inspirerad av komprimerad avkänning , med tillämpningar inom radar med syntetisk bländaröppning , datortomografiskanning och magnetisk resonanstomografi (MRI) .

Statistisk rekonstruktion

Det finns vanligtvis fem komponenter till statistiska iterativa bildrekonstruktionsalgoritmer, t.ex

1. En objektmodell som uttrycker den okända kontinuerliga rymdfunktionen $f(r)$ som ska rekonstrueras i termer av en ändlig serie med okända koefficienter som måste uppskattas från datan.
2. En systemmodell som relaterar det okända objektet till de "ideala" mätningarna som skulle registreras i frånvaro av mätbrus. Ofta är detta en linjär modell av formen ${\displaystyle \mathbf {A} x+\epsilon } ,$ där $\epsilon$ representerar bruset.
3. En statistisk modell som beskriver hur de bullriga mätningarna varierar kring deras idealvärden. Ofta antas Gaussiskt brus eller Poisson-statistik . Eftersom Poisson-statistiken ligger närmare verkligheten är den mer allmänt använd.
4. En kostnadsfunktion som ska minimeras för att uppskatta bildkoefficientvektorn. Ofta innefattar denna kostnadsfunktion någon form av regularisering . Ibland är regulariseringen baserad på Markovs slumpmässiga fält .
5. En algoritm , vanligtvis iterativ, för att minimera kostnadsfunktionen, inklusive en initial uppskattning av bilden och något stoppkriterium för att avsluta iterationerna.

Lärde iterativ rekonstruktion

I inlärd iterativ rekonstruktion lärs uppdateringsalgoritmen från träningsdata med hjälp av tekniker från maskininlärning såsom konvolutionella neurala nätverk , samtidigt som bildbildningsmodellen ingår. Detta ger vanligtvis snabbare och högre kvalitet rekonstruktioner och har tillämpats på CT och MRT rekonstruktion.

Fördelar

En enda bildruta från en realtids MRI (rt-MRI) film av ett mänskligt hjärta . a) direkt rekonstruktion b) iterativ (icke-linjär invers) rekonstruktion

Fördelarna med det iterativa tillvägagångssättet inkluderar förbättrad okänslighet för brus och förmågan att rekonstruera en optimal bild i fallet med ofullständiga data. Metoden har tillämpats i emissionstomografimodaliteter som SPECT och PET , där det finns betydande dämpning längs strålvägar och bullerstatistiken är relativt dålig.

Statistiska, sannolikhetsbaserade tillvägagångssätt : Statistiska, sannolikhetsbaserade iterativa förväntningsmaximeringsalgoritmer är nu den föredragna metoden för rekonstruktion. Sådana algoritmer beräknar uppskattningar av den sannolika fördelningen av annihilationshändelser som ledde till uppmätta data, baserat på statistisk princip, vilket ofta ger bättre brusprofiler och motstånd mot strimmiga artefakter som är vanliga med FBP. Eftersom densiteten av radioaktivt spårämne är en funktion i ett funktionsutrymme, därför av extremt höga dimensioner, kan metoder som reglerar lösningen med maximal sannolikhet genom att vända den mot straffade eller maximala a-posteriori-metoder ha betydande fördelar för låga värden. Exempel som Ulf Grenanders Sieve -estimator eller Bayes straffmetoder, eller via IJ Goods grovhetsmetod kan ge överlägsen prestanda jämfört med förväntningsmaximeringsbaserade metoder som endast involverar en Poisson-sannolikhetsfunktion.

Som ett annat exempel anses det vara överlägset när man inte har en stor uppsättning utsprång tillgängliga, när utsprången inte är jämnt fördelade i vinkel, eller när utsprången är glesa eller saknas i vissa orienteringar. Dessa scenarier kan förekomma vid intraoperativ CT, i hjärt- CT eller när metallartefakter kräver uteslutning av vissa delar av projektionsdata.

I magnetisk resonansavbildning kan den användas för att rekonstruera bilder från data som förvärvats med flera mottagningsspolar och med samplingsmönster som skiljer sig från det konventionella kartesiska rutnätet och tillåter användning av förbättrade regleringstekniker (t.ex. total variation ) eller en utökad modellering av fysiska processer för att förbättra rekonstruktionen. Till exempel, med iterativa algoritmer är det möjligt att rekonstruera bilder från data som förvärvats på mycket kort tid som krävs för realtids-MRI ( rt-MRI).

I Cryo Electron Tomography , där det begränsade antalet projektioner förvärvas på grund av hårdvarubegränsningarna och för att undvika skador på biologiska prover, kan den användas tillsammans med kompressionsavkänningstekniker eller regulariseringsfunktioner (t.ex. Huber-funktion ) för att förbättra rekonstruktionen för bättre tolkning .

Här är ett exempel som illustrerar fördelarna med iterativ bildrekonstruktion för hjärt-MR.

Se även

• Tomografisk rekonstruktion
• Positronemissionstomografi
• Tomogram
• Datortomografi
• Magnetisk resonanstomografi
• Omvänt problem
• Osem
• Dekonvolution
• Inmålning
• Algebraisk rekonstruktionsteknik
• iterativ gles asymptotisk minimumvarians