Isolinhämtning

Isolinhämtning är en omvänd metod för fjärravkänning som hämtar en eller flera isoliner av ett spår av atmosfärisk beståndsdel eller variabel. När det används för att validera en annan kontur är det den mest exakta metoden som är möjlig för uppgiften. När det används för att hämta ett helt fält är det en allmän, olinjär invers metod och en robust skattare.

För validering av adverade konturer

Logisk grund

Antag att vi, som i konturadvektion , har härledd kunskap om en enda kontur eller isolin av en atmosfärisk beståndsdel, q och vi vill validera detta mot satellitfjärravkänningsdata. Eftersom satellitinstrument inte kan mäta beståndsdelen direkt måste vi utföra någon form av inversion. För att validera konturen är det inte nödvändigt att veta det exakta värdet av beståndsdelen vid någon given punkt. Vi behöver bara veta om det faller inuti eller utanför, det vill säga är det större än eller mindre än värdet på konturen, q ₀ .

Detta är ett klassificeringsproblem. Låta:

$j={\begin{cases}1;&q<q_{0}\\2;&q\geq q_{0}\end{cases}}$

vara den diskretiserade variabeln. Detta kommer att relateras till satellitmätningsvektorn y $\displaystyle {\vec {y}}}$ , med viss villkorad sannolikhet, $)}$${\displaystyle P({\vec {y}}|$ j , som vi approximerar genom att samla in prover, kallade träningsdata , av både mätvektorn och tillståndsvariabeln, q . Genom att generera klassificeringsresultat över området av intresse och använda valfri konturalgoritm för att separera de två klasserna, kommer isolinen att ha "hämtats".

Noggrannheten för en hämtning kommer att ges genom att integrera den villkorade sannolikheten över det intressanta området, A :

$a={\frac {1}{A}}\int _{A}P\left[c({\vec {r}})|{\vec { y}}({\vec {r}})\right]\,d{\vec {r}}$

där c är den hämtade klassen vid position, ${\vec {r}}$ . Vi kan maximera denna kvantitet genom att maximera värdet av integranden vid varje punkt:

$\max(a)={\frac {1}{A}}\int _{A}\left\lbrace \max _{j}P\left[ j|{\vec {y}}({\vec {r}})\right]\right\rbrace \,d{\vec {r}}$

Eftersom detta är definitionen av maximal sannolikhet är en klassificeringsalgoritm baserad på maximal sannolikhet den mest exakta metoden som är möjlig för att validera en advected kontur. En bra metod för att utföra maximal sannolikhetsklassificering från en uppsättning träningsdata är uppskattning av variabel kärndensitet .

Träningsdata

Det finns två metoder för att generera träningsdata. Det mest uppenbara är empiriskt, genom att helt enkelt matcha mätningar av variabeln, q , med samlokaliserade mätningar från satellitinstrumentet. I det här fallet krävs ingen kunskap om den faktiska fysiken som producerar mätningen och hämtningsalgoritmen är rent statistisk. Den andra är med en framåtmodell:

${\vec {y}}={\vec {f}}({\vec {x}})\,$

där ${\vec {x}}$ är tillståndsvektorn och q = x _k är en enskild komponent. En fördel med denna metod är att tillståndsvektorer inte behöver återspegla faktiska atmosfäriska konfigurationer, de behöver bara anta ett tillstånd som rimligen skulle kunna inträffa i den verkliga atmosfären. Det finns inte heller några av de fel som är inneboende i de flesta samlokaliseringsprocedurer , t.ex. på grund av förskjutningsfel i placeringen av de parade proverna och skillnader i storleken på fotavtrycken för de två instrumenten. Eftersom hämtningar kommer att vara partiska mot vanligare tillstånd, bör dock statistiken återspegla dem i den verkliga världen.

Felkarakterisering

De villkorliga sannolikheterna, $P({\vec {y}}|j)$ , ger utmärkt felkarakterisering, därför borde klassificeringsalgoritmen returnera dem. Vi definierar konfidensbetyget genom att skala om den villkorade sannolikheten:

$C={\frac {n_{c}P(c|{\vec {y}})-1}{n_{c} -1}}$

där n _c är antalet klasser (i detta fall två). Om C är noll så är klassificeringen lite bättre än slumpen, medan om det är ett så borde den vara perfekt. För att omvandla konfidensgraden till en statistisk tolerans kan följande linjeintegral tillämpas på en isolinhämtning för vilken den sanna isolinen är känd:

$\delta (C)={\frac {1}{l}}\int _{0}^{l }h(CC^{\prime }({\vec {r}}))\,ds$

där s är banan, l är längden på isolinen och $C^{\prime }$ är den hämtade konfidensen som en funktion av position. Även om det verkar som att integralen måste utvärderas separat för varje värde i konfidensklassificeringen, C , kan det faktiskt göras för alla värden på C genom att sortera konfidensklassificeringarna för resultaten, $C^{\prime }$ . Funktionen relaterar tröskelvärdet för konfidensklassificeringen för vilken toleransen är tillämplig. Det vill säga, det definierar en region som innehåller en bråkdel av den sanna isolinen som är lika med toleransen.

Exempel: vattenånga från AMSU

Statistisk tolerans kontra konfidensklassificering för återvinning av vatten-ånga isoliner.

Advanced Microwave Sounding Unit (AMSU)-serien av satellitinstrument är designade för att detektera temperatur och vattenånga. De har en hög horisontell upplösning (så lite som 15 km) och eftersom de är monterade på mer än en satellit kan full global täckning erhållas på mindre än en dag. Träningsdata genererades med den andra metoden från European Centre for Medium-Range Weather Forecasts ( ECMWF) ERA-40-data som matades till en modell för snabb strålningsöverföring som kallas RTTOV . Funktionen $\delta (C)$ har genererats från simulerade hämtningar och visas i figuren till höger. Detta används sedan för att ställa in toleransen på 90 procent i figuren nedan genom att skugga alla konfidensvärden mindre än 0,8. Därför förväntar vi oss att den sanna isolinen faller inom skuggningen 90 procent av tiden.

Vattenånga isolin hämtat från AMSU mätningar och jämfört med ECMWF reanalys.

För kontinuerliga hämtningar

Specifik fuktighet kontra betingade sannolikheter från vatten-ånga isolinhämtning.

Isolinhämtning är också användbar för att hämta en kontinuumvariabel och utgör en allmän, icke-linjär invers metod . Det har fördelen jämfört med både ett neuralt nätverk , såväl som iterativa metoder som optimal uppskattning som inverterar framåtmodellen direkt, genom att det inte finns någon möjlighet att fastna i ett lokalt minimum .

Det finns ett antal metoder för att rekonstituera kontinuumvariabeln från den diskretiserade. När ett tillräckligt antal konturer har hämtats är det enkelt att interpolera mellan dem. Villkorade sannolikheter är en bra proxy för kontinuumvärdet.

Betrakta transformationen från ett kontinuum till en diskret variabel:

$P(1|{\vec {y}})=\int _{-\infty }^{q_{0 }}P(q|{\vec {y}})\,dq$

$P(2|{\vec {y }})=\int _{q_{0}}^{\infty }P(q|{\vec {y}})\,dq$

Antag att $P(q|{\vec {y}})$ ges av en gaussisk:

$P(q|{\vec {y}})={\ frac {1}{{\sqrt {2\pi }}\sigma _{q}}}\exp \left\lbrace -{\frac {\left[q-{\bar {q}}({\vec { y}})\right]^{2}}{2\sigma _{q}}}\right\rbrace$

där ${\bar {q}}$ är förväntningsvärdet och $\sigma _{q}$ är standardavvikelsen, då relateras den villkorliga sannolikheten till kontinuumvariabeln, q , med felfunktionen:

$R=P(2|{\vec {y}} )-P(1|{\vec {y}})=\mathrm {erf} \left[{\frac {q_{0}-{\bar {q}}({\vec {y}})}{ {\sqrt {2}}\sigma _{q}}}\right]$

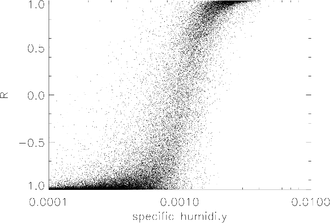
Figuren visar betingad sannolikhet kontra specifik luftfuktighet för exemplet hämtning som diskuterats ovan.

Som en robust estimerare

₀ Placeringen av q hittas genom att sätta de villkorliga sannolikheterna för de två klasserna till lika:

$\int _{-\infty }^{q_{0}}P(q|{\ vec {y}})\,dq=\int _{q_{0}}^{\infty }P(q|{\vec {y}})\,dq$

₀ Med andra ord, lika stora mängder av "momentet med nollte ordningen" ligger på vardera sidan av q . Denna typ av formulering är karakteristisk för en robust estimator .

• Peter Mills (2009). "Isolinhämtning: En optimal metod för validering av adverade konturer" ( PDF) . Datorer & Geovetenskap . 35 (11): 2020–2031. arXiv : 1202.5659 . Bibcode : 2009CG.....35.2020M . doi : 10.1016/j.cageo.2008.12.015 .

• Peter Mills (2010). "Effektiv statistisk klassificering av satellitmätningar" (PDF) . International Journal of Remote Sensing . arXiv : 1202.2194 . doi : 10.1080/01431161.2010.507795 . Arkiverad från originalet (PDF) 2012-04-26 . Hämtad 2011-12-28 .

externa länkar

• Programvara för isoline-hämtning