Iris blomma datauppsättning

Scatterplot av datamängden

Datauppsättningen Irisblommor sin eller Fishers Iris- datauppsättning är en multivariat datauppsättning som används och gjordes känd av den brittiske statistikern och biologen Ronald Fisher i uppsats från 1936 Användningen av flera mätningar i taxonomiska problem som ett exempel på linjär diskriminantanalys . Det kallas ibland Andersons Iris- datauppsättning eftersom Edgar Anderson samlade in data för att kvantifiera den morfologiska variationen av Irisblommor av tre besläktade arter. Två av de tre arterna samlades in på Gaspéhalvön "alla från samma bete, och plockades samma dag och mättes samtidigt av samma person med samma apparat".

Datauppsättningen består av 50 prover från var och en av tre arter av iris ( Iris setosa , Iris virginica och Iris versicolor) . Fyra egenskaper mättes från varje prov: längden och bredden på foderbladen och kronbladen , i centimeter. Baserat på kombinationen av dessa fyra egenskaper utvecklade Fisher en linjär diskriminantmodell för att skilja arterna från varandra. Fishers papper publicerades i Annals of Eugenics och inkluderar diskussioner om de inneslutna teknikernas tillämpningar på området frenologi .

Användning av datamängden

Otillfredsställande k-betyder klustring (data kan inte klustras i de kända klasserna) och faktiska arter visualiserade med ELKI

Ett exempel på den så kallade "metrokartan" för Iris- datauppsättningen Endast en liten del av Iris-virginica blandas med Iris-versicolor . Alla andra prover av de olika irisarterna tillhör de olika noderna.

Ursprungligen använd som ett exempel på datauppsättning som Fishers linjära diskriminantanalys tillämpades på, blev det ett typiskt testfall för många statistiska klassificeringstekniker inom maskininlärning, såsom stödvektormaskiner .

Användningen av denna datamängd i klusteranalys är dock inte vanlig, eftersom datamängden bara innehåller två kluster med ganska tydlig separation. Ett av klustren innehåller Iris setosa , medan det andra klustret innehåller både Iris virginica och Iris versicolor och går inte att separera utan den artinformation som Fisher använt. Detta gör datamängden till ett bra exempel för att förklara skillnaden mellan övervakad och oövervakad teknik inom datautvinning : Fishers linjära diskriminantmodell kan endast erhållas när objektsarten är kända: klassetiketter och kluster är inte nödvändigtvis desamma.

Ändå är alla tre arterna av iris separerbara i projektionen på den olinjära och förgrenande huvudkomponenten. Datauppsättningen uppskattas av det närmaste trädet med viss straff för det överdrivna antalet noder, böjning och sträckning. Sedan konstrueras den så kallade "tunnelbanekartan". Datapunkterna projiceras in i den närmaste noden. För varje nod upprättas cirkeldiagrammet för de projicerade punkterna. Området på pajen är proportionell mot antalet projicerade punkter. Det framgår tydligt av diagrammet (till vänster) att den absoluta majoriteten av proverna av de olika irisarterna tillhör de olika noderna. Endast en liten del av Iris-virginica blandas med Iris-versicolor (de blandade blågröna noderna i diagrammet). Därför kan de tre arterna av iris ( Iris setosa , Iris virginica och Iris versicolor ) separeras genom de oövervakande procedurerna för ickelinjär huvudkomponentanalys . För att särskilja dem är det tillräckligt att bara välja motsvarande noder på huvudträdet.

Datauppsättning

Iris setosa

Datauppsättningen innehåller en uppsättning av 150 poster under fem attribut - foderbladslängd, foderbladsbredd, kronbladslängd, kronbladsbredd och art.

Iris versicolor

Iris virginica

Spectramap biplot av Fishers irisdatauppsättning

Fishers Iris- data

Datauppsättningsordning	Foderbladslängd	Foderbladsbredd	Kronbladslängd	Kronbladsbredd	Arter
1	5.1	3.5	1.4	0,2	I. setosa
2	4.9	3.0	1.4	0,2	I. setosa
3	4.7	3.2	1.3	0,2	I. setosa
4	4.6	3.1	1.5	0,2	I. setosa
5	5.0	3.6	1.4	0,3	I. setosa
6	5.4	3.9	1.7	0,4	I. setosa
7	4.6	3.4	1.4	0,3	I. setosa
8	5.0	3.4	1.5	0,2	I. setosa
9	4.4	2.9	1.4	0,2	I. setosa
10	4.9	3.1	1.5	0,1	I. setosa
11	5.4	3.7	1.5	0,2	I. setosa
12	4.8	3.4	1.6	0,2	I. setosa
13	4.8	3.0	1.4	0,1	I. setosa
14	4.3	3.0	1.1	0,1	I. setosa
15	5.8	4.0	1.2	0,2	I. setosa
16	5.7	4.4	1.5	0,4	I. setosa
17	5.4	3.9	1.3	0,4	I. setosa
18	5.1	3.5	1.4	0,3	I. setosa
19	5.7	3.8	1.7	0,3	I. setosa
20	5.1	3.8	1.5	0,3	I. setosa
21	5.4	3.4	1.7	0,2	I. setosa
22	5.1	3.7	1.5	0,4	I. setosa
23	4.6	3.6	1.0	0,2	I. setosa
24	5.1	3.3	1.7	0,5	I. setosa
25	4.8	3.4	1.9	0,2	I. setosa
26	5.0	3.0	1.6	0,2	I. setosa
27	5.0	3.4	1.6	0,4	I. setosa
28	5.2	3.5	1.5	0,2	I. setosa
29	5.2	3.4	1.4	0,2	I. setosa
30	4.7	3.2	1.6	0,2	I. setosa
31	4.8	3.1	1.6	0,2	I. setosa
32	5.4	3.4	1.5	0,4	I. setosa
33	5.2	4.1	1.5	0,1	I. setosa
34	5.5	4.2	1.4	0,2	I. setosa
35	4.9	3.1	1.5	0,2	I. setosa
36	5.0	3.2	1.2	0,2	I. setosa
37	5.5	3.5	1.3	0,2	I. setosa
38	4.9	3.6	1.4	0,1	I. setosa
39	4.4	3.0	1.3	0,2	I. setosa
40	5.1	3.4	1.5	0,2	I. setosa
41	5.0	3.5	1.3	0,3	I. setosa
42	4.5	2.3	1.3	0,3	I. setosa
43	4.4	3.2	1.3	0,2	I. setosa
44	5.0	3.5	1.6	0,6	I. setosa
45	5.1	3.8	1.9	0,4	I. setosa
46	4.8	3.0	1.4	0,3	I. setosa
47	5.1	3.8	1.6	0,2	I. setosa
48	4.6	3.2	1.4	0,2	I. setosa
49	5.3	3.7	1.5	0,2	I. setosa
50	5.0	3.3	1.4	0,2	I. setosa
51	7,0	3.2	4.7	1.4	I. versicolor
52	6.4	3.2	4.5	1.5	I. versicolor
53	6.9	3.1	4.9	1.5	I. versicolor
54	5.5	2.3	4.0	1.3	I. versicolor
55	6.5	2.8	4.6	1.5	I. versicolor
56	5.7	2.8	4.5	1.3	I. versicolor
57	6.3	3.3	4.7	1.6	I. versicolor
58	4.9	2.4	3.3	1.0	I. versicolor
59	6.6	2.9	4.6	1.3	I. versicolor
60	5.2	2.7	3.9	1.4	I. versicolor
61	5.0	2.0	3.5	1.0	I. versicolor
62	5.9	3.0	4.2	1.5	I. versicolor
63	6,0	2.2	4.0	1.0	I. versicolor
64	6.1	2.9	4.7	1.4	I. versicolor
65	5.6	2.9	3.6	1.3	I. versicolor
66	6.7	3.1	4.4	1.4	I. versicolor
67	5.6	3.0	4.5	1.5	I. versicolor
68	5.8	2.7	4.1	1.0	I. versicolor
69	6.2	2.2	4.5	1.5	I. versicolor
70	5.6	2.5	3.9	1.1	I. versicolor
71	5.9	3.2	4.8	1.8	I. versicolor
72	6.1	2.8	4.0	1.3	I. versicolor
73	6.3	2.5	4.9	1.5	I. versicolor
74	6.1	2.8	4.7	1.2	I. versicolor
75	6.4	2.9	4.3	1.3	I. versicolor
76	6.6	3.0	4.4	1.4	I. versicolor
77	6.8	2.8	4.8	1.4	I. versicolor
78	6.7	3.0	5.0	1.7	I. versicolor
79	6,0	2.9	4.5	1.5	I. versicolor
80	5.7	2.6	3.5	1.0	I. versicolor
81	5.5	2.4	3.8	1.1	I. versicolor
82	5.5	2.4	3.7	1.0	I. versicolor
83	5.8	2.7	3.9	1.2	I. versicolor
84	6,0	2.7	5.1	1.6	I. versicolor
85	5.4	3.0	4.5	1.5	I. versicolor
86	6,0	3.4	4.5	1.6	I. versicolor
87	6.7	3.1	4.7	1.5	I. versicolor
88	6.3	2.3	4.4	1.3	I. versicolor
89	5.6	3.0	4.1	1.3	I. versicolor
90	5.5	2.5	4.0	1.3	I. versicolor
91	5.5	2.6	4.4	1.2	I. versicolor
92	6.1	3.0	4.6	1.4	I. versicolor
93	5.8	2.6	4.0	1.2	I. versicolor
94	5.0	2.3	3.3	1.0	I. versicolor
95	5.6	2.7	4.2	1.3	I. versicolor
96	5.7	3.0	4.2	1.2	I. versicolor
97	5.7	2.9	4.2	1.3	I. versicolor
98	6.2	2.9	4.3	1.3	I. versicolor
99	5.1	2.5	3.0	1.1	I. versicolor
100	5.7	2.8	4.1	1.3	I. versicolor
101	6.3	3.3	6,0	2.5	I. virginica
102	5.8	2.7	5.1	1.9	I. virginica
103	7.1	3.0	5.9	2.1	I. virginica
104	6.3	2.9	5.6	1.8	I. virginica
105	6.5	3.0	5.8	2.2	I. virginica
106	7.6	3.0	6.6	2.1	I. virginica
107	4.9	2.5	4.5	1.7	I. virginica
108	7.3	2.9	6.3	1.8	I. virginica
109	6.7	2.5	5.8	1.8	I. virginica
110	7.2	3.6	6.1	2.5	I. virginica
111	6.5	3.2	5.1	2.0	I. virginica
112	6.4	2.7	5.3	1.9	I. virginica
113	6.8	3.0	5.5	2.1	I. virginica
114	5.7	2.5	5.0	2.0	I. virginica
115	5.8	2.8	5.1	2.4	I. virginica
116	6.4	3.2	5.3	2.3	I. virginica
117	6.5	3.0	5.5	1.8	I. virginica
118	7.7	3.8	6.7	2.2	I. virginica
119	7.7	2.6	6.9	2.3	I. virginica
120	6,0	2.2	5.0	1.5	I. virginica
121	6.9	3.2	5.7	2.3	I. virginica
122	5.6	2.8	4.9	2.0	I. virginica
123	7.7	2.8	6.7	2.0	I. virginica
124	6.3	2.7	4.9	1.8	I. virginica
125	6.7	3.3	5.7	2.1	I. virginica
126	7.2	3.2	6,0	1.8	I. virginica
127	6.2	2.8	4.8	1.8	I. virginica
128	6.1	3.0	4.9	1.8	I. virginica
129	6.4	2.8	5.6	2.1	I. virginica
130	7.2	3.0	5.8	1.6	I. virginica
131	7.4	2.8	6.1	1.9	I. virginica
132	7.9	3.8	6.4	2.0	I. virginica
133	6.4	2.8	5.6	2.2	I. virginica
134	6.3	2.8	5.1	1.5	I. virginica
135	6.1	2.6	5.6	1.4	I. virginica
136	7.7	3.0	6.1	2.3	I. virginica
137	6.3	3.4	5.6	2.4	I. virginica
138	6.4	3.1	5.5	1.8	I. virginica
139	6,0	3.0	4.8	1.8	I. virginica
140	6.9	3.1	5.4	2.1	I. virginica
141	6.7	3.1	5.6	2.4	I. virginica
142	6.9	3.1	5.1	2.3	I. virginica
143	5.8	2.7	5.1	1.9	I. virginica
144	6.8	3.2	5.9	2.3	I. virginica
145	6.7	3.3	5.7	2.5	I. virginica
146	6.7	3.0	5.2	2.3	I. virginica
147	6.3	2.5	5.0	1.9	I. virginica
148	6.5	3.0	5.2	2.0	I. virginica
149	6.2	3.4	5.4	2.3	I. virginica
150	5.9	3.0	5.1	1.8	I. virginica

Irisdatauppsättningen används ofta som en nybörjardatauppsättning för maskininlärningsändamål. Datauppsättningen ingår i R base och Python i maskininlärningsbiblioteket scikit-learn , så att användare kan komma åt det utan att behöva hitta en källa för det.

Flera versioner av datasetet har publicerats.

R -kod som illustrerar användning

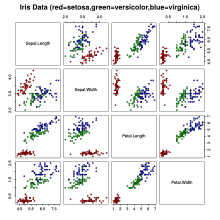
Exempel R-koden som visas nedan återger spridningsdiagrammet som visas överst i den här artikeln:

 
        # Visa datasetets  iris  # Visa hjälpsidan, med information om datasetet  ?  iris  # Skapa spridningsdiagram av alla parvisa kombinationer av de 4 variablerna i datasetparen  (  iris  [  1  :  4  ]  ,  main  =  "Iris Data (röd=setosa, grön=versicolor, blå=virginica)"  ,  pch  =  21  ,  bg  =  c  (  "röd"  ,  "grön3"  ,  "blå"  )[  oklass  (  iris  $  Art )  ]) 

Python -kod som illustrerar användning

   

  
 från  sklearn.datasets  import  load_iris  iris  =  load_iris  ()  iris 

Denna kod ger:

    
                    
                   
                   
 0 0 0         
     
 {  'data'  :  array  ([[  5.1  ,  3.5  ,  1.4  ,  0.2  ],  [  4.9  ,  3.  ,  1.4  ,  0.2  ],  [  4.7  ,  3.2  ,  1.3  ,  0.2  ],  [  4.6  ,  3.51  ,  3.51  ,  3.51  , 3  . ..  'target'  :  array  ([  ,  ,  ,  ...  1  ,  1  ,  1  ,  ...  2  ,  2  ,  2  ,  ...  'target_names'  :  array  ([  'setosa'  ,  'versicolor'  ,  'virginica '  ],  dtype  =  '<U10'  ),  ...  } 

Se även

• Klassiska datamängder
• Lista över datauppsättningar för forskning om maskininlärning

externa länkar

• "Fishers Iris Data" . (Innehåller två fel som är dokumenterade) . UCI Machine Learning Repository: Iris Data Set.