HSL och HSV

Fig. 1. HSL (a–d) och HSV (e–h). Ovan (a, e): utskurna 3D-modeller av varje. Nedan: tvådimensionella diagram som visar två av en modells tre parametrar samtidigt, och håller den andra konstant: cylindriska skal (b, f) med konstant mättnad, i detta fall utsidan av varje cylinder; horisontella tvärsnitt (c, g) med konstant HSL-lätthet eller HSV-värde, i detta fall skivorna halvvägs ner för varje cylinder; och rektangulära vertikala tvärsnitt (d, h) med konstant nyans, i detta fall av nyanser 0° röd och dess komplement 180° cyan.

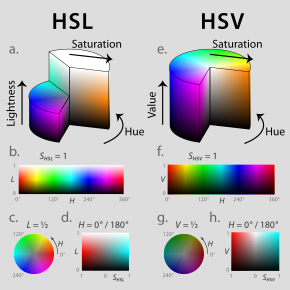
HSL (för nyans, saturation, ljushet ) och HSV (för nyans, saturation, värde ; även känd som HSB , för nyans, saturation, ljushet ) är alternativa representationer av RGB - färgmodellen , designad på 1970-talet av datorgrafikforskare för att mer nära överensstämmelse med hur människans syn uppfattar färgskapande egenskaper. I dessa modeller är färgerna i varje nyans arrangerade i en radiell skiva, runt en central axel av neutrala färger som sträcker sig från svart längst ner till vitt upptill.

HSL-representationen modellerar hur olika färger blandas ihop för att skapa färg i den verkliga världen, med ljushetsdimensionen som liknar de varierande mängderna svart eller vit färg i blandningen (t.ex. för att skapa "ljusröd", kan ett rött pigment blandas med vit färg; denna vita färg motsvarar ett högt "lätthetsvärde" i HSL-representationen). Helt mättade färger placeras runt en cirkel med ett ljushetsvärde på ½, med ett ljushetsvärde på 0 eller 1 motsvarande helt svart respektive vitt.

Samtidigt modellerar HSV-representationen hur färger visas under ljus. Skillnaden mellan HSL och HSV är att en färg med maximal ljushet i HSL är rent vit, men en färg med maximalt värde/ljusstyrka i HSV är analog med att lysa ett vitt ljus på ett färgat föremål (t.ex. att lysa ett starkt vitt ljus på ett rött objekt gör att objektet fortfarande ser rött ut, bara ljusare och mer intensivt, medan ett svagt ljus lyser på ett rött objekt gör att objektet ser mörkare och mindre ljust ut).

Problemet med både HSV och HSL är att dessa metoder inte effektivt separerar färg i sina tre värdekomponenter enligt människans uppfattning om färg. Detta kan ses när mättnadsinställningarna ändras - det är ganska lätt att märka skillnaden i perceptuell ljushet trots att "V" eller "L" är fixerade.

Grundläggande princip

Fig. 2a. HSL cylinder.

Fig. 2b. HSV cylinder.

HSL och HSV är båda cylindriska geometrier ( fig. 2 ), med nyans, deras vinkeldimension, som börjar vid den röda primären vid 0°, passerar genom den gröna primären vid 120° och den blå primären vid 240°, för att sedan svepa tillbaka till röd vid 360°. I varje geometri omfattar den centrala vertikala axeln de neutrala , akromatiska eller grå färgerna som sträcker sig från topp till botten, vit vid ljushet 1 (värde 1) till svart vid ljushet 0 (värde 0).

I båda geometrierna är de additiva primära och sekundära färgerna – röd, gul , grön, cyan , blå och magenta – och linjära blandningar mellan angränsande par av dem, ibland kallade rena färger , arrangerade runt cylinderns yttre kant med mättnad 1. Dessa mättade färger har ljushet 0,5 i HSL, medan de i HSV har värde 1. Blandning av dessa rena färger med svart – ger så kallade nyanser – lämnar mättnaden oförändrad. I HSL är mättnaden också oförändrad genom färgning med vitt, och endast blandningar med både svart och vitt – så kallade toner – har en mättnad mindre än 1. I HSV minskar enbart färgning mättnaden.

Fig. 3a–b. Om vi ​​plottar nyans och (a) HSL-ljushet eller (b) HSV-värde mot chroma ( intervall av RGB-värden) snarare än mättnad (chroma över maximal chroma för den skivan), är det resulterande fasta materialet en bicone respektive kon , inte en cylinder. Sådana diagram gör ofta anspråk på att representera HSL eller HSV direkt, med kromadimensionen förvirrande märkt "mättnad".

   Eftersom dessa definitioner av mättnad – där mycket mörka (i båda modellerna) eller mycket ljusa (i HSL) nästan neutrala färger anses vara helt mättade (till exempel nere till höger i den skivade HSL-cylindern eller uppe till höger) – i konflikt med den intuitiva uppfattningen om färgrenhet, ritas ofta en konisk eller bikonisk fast substans istället ( fig. 3 ), med vad denna artikel kallar chroma som dess radiella dimension (lika med intervallet för RGB-värdena), istället för mättnad (där mättnaden är lika med chroma över maximal chroma i den biten av (bi)konen). Förvirrande nog brukar sådana diagram märka denna radiella dimension som "mättnad", vilket suddar ut eller raderar skillnaden mellan mättnad och färg. Som beskrivs nedan är beräkning av chroma ett användbart steg i härledningen av varje modell. Eftersom en sådan mellanmodell – med dimensioner nyans, kromatografi och HSV-värde eller HSL-ljushet – tar formen av en kon eller bikon, kallas HSV ofta för "hexkonmodellen" medan HSL ofta kallas "bi-hexkonmodellen" ( fig. 8 ).

Motivering

Se även: Färgteori , RGB-färgmodell och RGB-färgrymd

HSL-färgrymden uppfanns för TV 1938 av Georges Valensi som en metod för att lägga till färgkodning till befintliga monokroma (dvs. innehåller endast L-signalen) sändningar, vilket gör det möjligt för befintliga mottagare att ta emot nya färgsändningar (i svartvitt) utan modifiering som luminanssignalen (svartvit) sänds oförändrad . Den har använts i alla större analoga TV-sändningar inklusive NTSC , PAL och SECAM och alla större digitala sändningssystem och är grunden för kompositvideo .

Fig. 4. Målar länge blandade färger genom att kombinera relativt ljusa pigment med svart och vitt. Blandningar med vitt kallas nyanser , blandningar med svart kallas nyanser och blandningar med båda kallas toner . Se Nyanser och nyanser .

Fig. 5. Denna färgmodell från 1916 av den tyske kemisten Wilhelm Ostwald exemplifierar metoden "blandningar med vitt och svart", och organiserar 24 "rena" färger i en nyanscirkel och färgerna för varje nyans i en triangel. Modellen tar alltså formen av en bicon.

Fig. 6a. RGB-omfånget kan ordnas i en kub.

Fig. 6b. Samma bild, med en del borttagen för tydlighetens skull.

Fig. 7. Tektronix grafikterminaler använde den tidigaste kommersiella implementeringen av HSL, 1979. Detta diagram, från ett patent inlämnat 1983, visar bikongeometrin som ligger till grund för modellen.

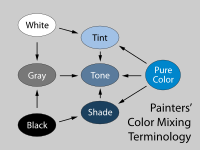
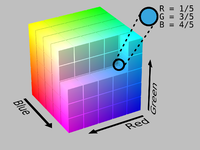
De flesta tv-apparater, datorskärmar och projektorer producerar färger genom att kombinera rött, grönt och blått ljus i olika intensiteter – de så kallade RGB - additiva primärfärgerna . De resulterande blandningarna i RGB-färgrymden kan reproducera en mängd olika färger (kallas en gamut ); dock är förhållandet mellan de ingående mängderna rött, grönt och blått ljus och den resulterande färgen ointuitivt, särskilt för oerfarna användare, och för användare som är bekanta med subtraktiv färgblandning av färger eller traditionella konstnärsmodeller baserade på nyanser och nyanser ( fig . 4 ). Dessutom definierar varken additiva eller subtraktiva färgmodeller färgförhållanden på samma sätt som det mänskliga ögat gör.

   Föreställ dig till exempel att vi har en RGB-skärm vars färg styrs av tre skjutreglage från 0–255 , en som styr intensiteten för var och en av de röda, gröna och blå primärerna. Om vi ​​börjar med en relativt färgstark apelsin , med sRGB- värden R = 217 , G = 118 , B = 33 , och vill minska dess färgstarka med hälften till en mindre mättad apelsin, skulle vi behöva dra reglagen för att minska R med 31 , öka G med 24 och öka B med 59, som bilden nedan.

I ett försök att tillgodose mer traditionella och intuitiva färgblandningsmodeller, introducerade datorgrafikpionjärer vid PARC och NYIT HSV-modellen för datorskärmsteknik i mitten av 1970-talet, formellt beskriven av Alvy Ray Smith i augusti 1978-numret av Computer Graphics . I samma nummer beskrev Joblove och Greenberg HSL-modellen – vars dimensioner de märkte nyans , relativ kroma och intensitet – och jämförde den med HSV ( fig. 1 ). Deras modell baserades mer på hur färger organiseras och konceptualiseras i människans syn i termer av andra färgskapande attribut, såsom nyans, ljushet och färg; såväl som på traditionella färgblandningsmetoder – t.ex. i målning – som innebär att färgglada pigment blandas med svart eller vitt för att uppnå ljusare, mörkare eller mindre färgglada färger.

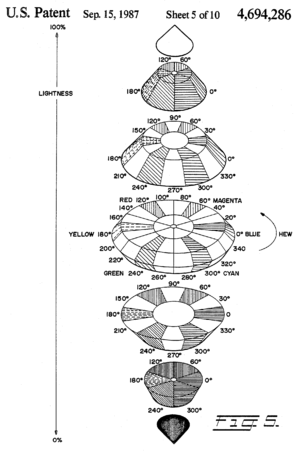
Följande år, 1979, på SIGGRAPH , introducerade Tektronix grafikterminaler som använder HSL för färgbeteckning, och Computer Graphics Standards Committee rekommenderade det i sin årliga statusrapport ( fig. 7 ). Dessa modeller var användbara inte bara för att de var mer intuitiva än råa RGB-värden, utan också för att omvandlingarna till och från RGB var extremt snabba att beräkna: de kunde köras i realtid på 1970-talets hårdvara. Följaktligen har dessa modeller och liknande blivit överallt i bildredigering och grafikprogram sedan dess. Några av deras användningsområden beskrivs nedan .

Formell härledning

Fig. 8. Den geometriska härledningen av de cylindriska HSL- och HSV-representationerna av en RGB-"färgkub".

Visualiserad geometrisk härledning av den cylindriska HSV-representationen av en RGB "colorcube".

Visualiserad geometrisk härledning av den cylindriska HSL-representationen av en RGB "colorcube".

Färgtillverkningsattribut

Se även: Färgseende

Dimensionerna för HSL- och HSV-geometrierna – enkla transformationer av den icke-perceptuellt baserade RGB-modellen – är inte direkt relaterade till de fotometriska färgtillverkningsattributen med samma namn, som definierats av forskare som CIE eller ASTM . Icke desto mindre är det värt att granska dessa definitioner innan vi går in i härledningen av våra modeller. För definitionerna av färgtillverkningsattribut som följer, se:

Nyans

"Attributet för en visuell känsla enligt vilken ett område verkar likna en av de upplevda färgerna : röd, gul, grön och blå, eller en kombination av två av dem".

Radians ( L _e,Ω )

Strålningseffekten av ljus som passerar genom en viss yta per enhet rymdvinkel per enhet projicerad area, mätt i SI-enheter i watt per steradian per kvadratmeter ( W·sr ⁻¹ ·m ⁻² ) .

Luminans ( Y eller L _v,Ω )

Radiansen viktad av effekten av varje våglängd på en typisk mänsklig observatör, mätt i SI-enheter i candela per kvadratmeter ( cd/m ² ). Ofta används termen luminans för den relativa luminansen , Y / Yn _, där Yn är luminansen för referensvitpunkten _.

Luma ( Y′ )

Den viktade summan av gammakorrigerade R ′ , G ′ och B ′ -värden, som används i Y′CbCr , för JPEG -komprimering och videoöverföring.

Ljusstyrka (eller värde)

"Attributet för en visuell känsla enligt vilken ett område verkar avge mer eller mindre ljus".

Ljusstyrka

"Ljusstyrkan i förhållande till ljusstyrkan hos en på liknande sätt upplyst vit".

Colorfulness

"Attributet för en visuell sensation enligt vilken den upplevda färgen på ett område verkar vara mer eller mindre kromatisk".

Chroma

Den "färgfullhet i förhållande till ljusstyrkan hos en på samma sätt upplyst vit".

Mättnad

"färgfullheten hos en stimulans i förhållande till dess egen ljusstyrka".

Ljusstyrka och färgstarkhet är absoluta mått, som vanligtvis beskriver den spektrala fördelningen av ljus som kommer in i ögat, medan ljushet och kromatografi mäts i förhållande till någon vit punkt, och används därför ofta för beskrivningar av ytfärger, förblir ungefär konstanta även som ljusstyrka och färgstarkhet. ändras med annan belysning . Mättnad kan definieras som antingen förhållandet mellan färgstarka och ljusstyrka, eller förhållandet mellan färg och ljushet.

Allmän riktlinje

HSL, HSV och relaterade modeller kan härledas via geometriska strategier, eller kan ses som specifika instanser av en "generaliserad LHS-modell". HSL- och HSV-modellbyggarna tog en RGB-kub – med ingående mängder av rött, grönt och blått ljus i en färg som betecknas R , G , B ∈ [0, 1] – och lutade den på sitt hörn så att svart vilade vid utgångspunkten med vitt direkt ovanför den längs den vertikala axeln, mätte sedan nyansen av färgerna i kuben efter deras vinkel runt den axeln, med början med rött vid 0°. Sedan kom de fram till en karakterisering av ljusstyrka/värde/ljushet, och definierade mättnad till att sträcka sig från 0 längs axeln till 1 vid den mest färgstarka punkten för varje par av andra parametrar.

Nyans och färgton

Se även: Nyans och krominans

Fig. 9. Både nyans och färgton definieras baserat på projektionen av RGB-kuben på en hexagon i "kromaticitetsplanet". Chroma är den relativa storleken på den hexagon som passerar genom en punkt, och nyans är hur långt runt den hexagonens kant punkten ligger.

I var och en av våra modeller beräknar vi både nyans och vad den här artikeln kommer att kalla chroma , efter Joblove och Greenberg (1978), på samma sätt – det vill säga att färgens nyans har samma numeriska värden i alla dessa modeller, liksom dess färg. Om vi ​​tar vår lutade RGB-kub och projicerar den på "kromaticitetsplanet " vinkelrätt mot den neutrala axeln, får vår projektion formen av en hexagon, med rött, gult, grönt, cyan, blått och magenta i sina hörn ( fig . 9 ). Nyans är ungefär vinkeln för vektorn till en punkt i projektionen, med rött vid 0°, medan chroma är ungefär avståndet mellan punkten från origo.

Mer exakt definieras både nyans och kromatografi i denna modell med avseende på den hexagonala formen på projektionen. Kroma är proportionen av avståndet från origo till kanten av hexagonen . I den nedre delen av det intilliggande diagrammet är detta förhållandet mellan längderna OP / OP ′ , eller alternativt förhållandet mellan radierna för de två hexagonerna. Detta förhållande är skillnaden mellan de största och minsta värdena bland R , G eller B i en färg. För att göra våra definitioner lättare att skriva, kommer vi att definiera dessa max-, minimum- och chroma-komponentvärden som M , m , respektive C .

$M=\max(R,G,B)$

$m=\min(R,G,B)$

$C=\operatörsnamn {range} (R,G,B)=Mm$

För att förstå varför chroma kan skrivas som M − m , lägg märke till att vilken neutral färg som helst, med R = G = B , projicerar på origo och så har 0 chroma. Om vi ​​alltså adderar eller subtraherar samma mängd från alla tre av R , G och B , rör vi oss vertikalt inom vår lutade kub och ändrar inte projektionen. Därför projicerar två valfria färger av ( R , G , B ) och ( R − m , G − m , B − m ) ut på samma punkt och har samma färg. Kroman för en färg med en av dess komponenter lika med noll ( m = 0) är helt enkelt det maximala av de andra två komponenterna. Denna chroma är M i det speciella fallet med en färg med en nollkomponent, och M − m i allmänhet.

Nyansen är andelen av avståndet runt kanten av hexagonen som passerar genom den projicerade punkten, ursprungligen mätt i området [ 0, 1] men nu vanligtvis mätt i grader [ 0°, 360°] . För punkter som projicerar ut på origo i kromaticitetsplanet (dvs. grått), är nyansen odefinierad. Matematiskt är denna definition av nyans skriven bitvis :

$H'={\begin{cases}\mathrm {undefined} ,&{\text{if }}C=0\\{\frac {GB}{C}}{\bmod {6}},& {\text{if }}M=R\\{\frac {BR}{C}}+2,&{\text{if }}M=G\\{\frac {RG}{C}}+4 ,&{\text{if }}M=B\end{cases}}$

$H=60^{\circ }\times H'$

tilldelas neutrala färger (dvs med C = 0 ) en nyans på 0° för att underlätta representationen.

Fig. 10. Definitionerna av nyans och kromatografi i HSL och HSV har effekten av att förvränga hexagoner till cirklar.

Dessa definitioner motsvarar en geometrisk skevning av hexagoner till cirklar: varje sida av hexagonen är avbildad linjärt på en 60° cirkelbåge ( fig. 10 ). Efter en sådan transformation är nyansen just vinkeln runt origo och chroma avståndet från origo: vinkeln och storleken på vektorn som pekar mot en färg.

Fig. 11. Att konstruera rektangulära kromaticitetskoordinater α och β och sedan omvandla dessa till nyans H ₂ och chroma C ₂ ger något annorlunda värden än att beräkna den hexagonala nyansen H och chroma C : jämför siffrorna i detta diagram med de tidigare i detta avsnitt.

Ibland för bildanalystillämpningar hoppas denna hexagon-till-cirkel-transformation över, och färgton och färgton (vi betecknar dessa H ₂ och C ₂ ) definieras av de vanliga kartesiska-till-polära koordinattransformationerna ( fig. 11 ). Det enklaste sättet att härleda dessa är via ett par kartesiska kromaticitetskoordinater som vi kallar α och β :

$\alpha =RG\cdot \cos(60^{\circ } )-B\cdot \cos(60^{\circ })={\tfrac {1}{2}}(2R-GB)$

$\beta =G\cdot \sin(60^{\circ })-B\cdot \sin(60^{\circ})={\tfrac {\sqrt { 3}}{2}}(GB)$

$H_{2}=\operatörsnamn {atan2} (\beta ,\alpha )$

$C_{2}=\operatörsnamn {gmean} (\alpha ,\beta )={\sqrt {\alpha ^{2}+\beta ^{2}}}$

( Atan2- funktionen, en "arctangens med två argument", beräknar vinkeln från ett kartesiskt koordinatpar.)

Lägg märke till att dessa två definitioner av nyans ( H och H ₂ ) nästan sammanfaller, med en maximal skillnad mellan dem för vilken färg som helst på cirka 1,12° - vilket förekommer vid tolv speciella nyanser, till exempel H = 13,38° , H ₂ = 12,26° - och med H = H ₂ för varje multipel av 30°. De två definitionerna av chroma ( C och C ₂ ) skiljer sig mer väsentligt åt: de är lika i hörnen av vår hexagon, men vid punkter halvvägs mellan två hörn, såsom H = H ₂ = 30° , har vi C = 1 , men C2 = √ ¾ ≈ 0,866 , en skillnad _på cirka 13,4%.

Lätthet

Fig. 12a–d. Fyra olika möjliga "lätthet"-dimensioner, plottade mot kromatografi, för ett par komplementära nyanser. Varje plot är ett vertikalt tvärsnitt av dess tredimensionella fasta färg.

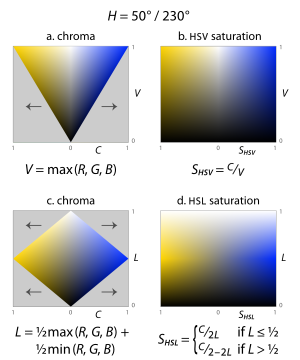
Även om definitionen av nyans är relativt okontroversiell – den uppfyller i stort sett kriteriet att färger av samma upplevda nyans ska ha samma numeriska nyans – är definitionen av en ljushets- eller värdedimension mindre uppenbar: det finns flera möjligheter beroende på syftet och målen. av representationen. Här är fyra av de vanligaste ( fig. 12 ; tre av dessa visas också i fig. 8 ):

• Den enklaste definitionen är bara det aritmetiska medelvärdet , dvs medelvärdet, av de tre komponenterna, i HSI-modellen som kallas intensitet ( fig. 12a ). Detta är helt enkelt projiceringen av en punkt på den neutrala axeln – den vertikala höjden av en punkt i vår lutande kub. Fördelen är att denna representation, tillsammans med euklidiska avståndsberäkningar av nyans och färgton, bevarar avstånd och vinklar från RGB-kubens geometri.

  $I=\operatörsnamn {avg} (R,G,B)={\tfrac {1}{3}}( R+G+B)$

• I HSV "hexcone"-modellen definieras värde som den största komponenten i en färg, vårt M ovan ( fig. 12b ) . Detta placerar alla tre primärfärgerna, och även alla "sekundära färger" - cyan, gult och magenta - i ett plan med vitt, som bildar en sexkantig pyramid av RGB-kuben.

  $V=\max(R,G,B)=M$

• I HSL "bi-hexcone"-modellen definieras ljushet som medelvärdet av de största och minsta färgkomponenterna ( fig. 12c ), dvs mellanområdet för RGB-komponenterna. Denna definition sätter också de primära och sekundära färgerna i ett plan, men ett plan som passerar halvvägs mellan vitt och svart. Den resulterande färgen är en dubbelkon som liknar Ostwalds, som visas ovan .

  $L=\operatörsnamn {mid} (R,G,B)={\tfrac {1}{2}}(M+ m)$

• Ett mer perceptuellt relevant alternativ är att använda luma , Y′ , som en ljushetsdimension ( fig. 12d) . Luma är det viktade medelvärdet av gammakorrigerade R , G och B , baserat på deras bidrag till upplevd ljushet, som länge använts som den monokromatiska dimensionen i färg-tv-sändningar. För sRGB är Rec. 709 primärer ger Y′ ₇₀₉ , digital NTSC använder Y′ ₆₀₁ enligt Rec. 601 och några andra primärer används också som resulterar i olika koefficienter.

  $=0.2989\cdot R+0.5870\cdot G$ { \text{601}

  $\text{240}}=0,212\cdot R+0,701\cdot G+0,087\cdot B} ($ Adobe)

  $0,7152\cdot G+0,0722\cdot B} ($ HDTV)

  ${\displaystyle Y'_{\text{2020}}=0,2627\cdot R+0,6780\cdot G+0,0593\cdot B} ($ UHDTV, HDR)

Alla fyra lämnar den neutrala axeln ifred. Det vill säga, för färger med R = G = B , ger vilken som helst av de fyra formuleringarna en ljushet som är lika med värdet av R , G eller B.

För en grafisk jämförelse, se fig. 13 nedan .

Mättnad

Fig. 14a–d. I både HSL och HSV mättnad helt enkelt den kroma som skalas för att fylla intervallet [0, 1] för varje kombination av nyans och ljushet eller värde.

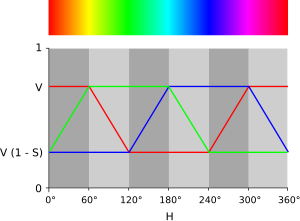
Vid kodning av färger i en nyans/ljushet/krom- eller nyans/värde/krom-modell (med definitionerna från de två föregående avsnitten), är inte alla kombinationer av ljushet (eller värde) och färger meningsfulla: det vill säga hälften av färgerna kan betecknas med H ∈ [0°, 360°) , faller C ∈ [0, 1] och V ∈ [0, 1] utanför RGB-omfånget (de grå delarna av skivorna i figur 14). Skaparna av dessa modeller ansåg att detta var ett problem för vissa användningsområden. Till exempel, i ett färgvalsgränssnitt med två av dimensionerna i en rektangel och den tredje på ett skjutreglage, är hälften av den rektangeln gjord av oanvänt utrymme. Föreställ dig nu att vi har ett skjutreglage för lätthet: användarens avsikt när han justerar skjutreglaget är potentiellt tvetydig: hur ska programvaran hantera färger utanför spektrumet? Eller omvänt, om användaren har valt en mörklila så färgstark som möjligt   ljushet uppåt, vad ska man göra: skulle användaren föredra att se en ljusare lila fortfarande så färgstark som möjligt för den givna nyansen och ljusheten   , eller en ljusare lila med exakt samma färg som originalfärgen   ?

För att lösa problem som dessa, skalar HSL- och HSV-modellerna chroma så att den alltid passar in i området [0, 1] för varje kombination av nyans och ljushet eller värde, vilket kallar det nya attributet saturation i båda fallen (fig. 14) ). För att beräkna endera, dividera helt enkelt kroma med maximal kroma för det värdet eller ljusheten.

$S_{V}={\begin{cases}0,&{\text{if }}V=0\\{\frac {C}{V} },&{\text{annars}}\end{cases}}$

$S_{L}={\begin{cases}0,&{\text{if }}L=1{\text{ eller }}L=0\\{\frac {C}{1- |2L-1|}},&{\text{annars}}\end{case}}$

Fig. 15a–b. I HSI är mättnad , som visas i skivan till höger, ungefär kromatografin i förhållande till ljushet. Vanlig är också en modell med dimensionerna I , H ₂ , C ₂ , som visas i skivan till vänster. Lägg märke till att nyansen i dessa skivor är densamma som nyansen ovan, men H skiljer sig något från H ₂ .

HSI-modellen som vanligtvis används för datorseende, som tar H ₂ som en nyansdimension och komponentens medelvärde I ("intensitet") som en lätthetsdimension, försöker inte "fylla" en cylinder enligt dess definition av mättnad. Istället för att presentera färgval eller modifieringsgränssnitt för slutanvändare, är målet med HSI att underlätta separation av former i en bild. Mättnad definieras därför i linje med den psykometriska definitionen: kroma relativt lätthet ( fig. 15 ). Se Använd i bildanalys i den här artikeln.

$S_{I}={\begin{cases}0,&{\text{if }}I=0\\1-{\frac {m }{I}},&{\text{annars}}\end{cases}}$

Att använda samma namn för dessa tre olika definitioner av mättnad leder till viss förvirring, eftersom de tre attributen beskriver väsentligt olika färgförhållanden; i HSV och HSI stämmer begreppet ungefär överens med den psykometriska definitionen av en chroma av en färg i förhållande till dess egen ljushet, men i HSL kommer den inte i närheten. Ännu värre, ordet saturation används också ofta för en av de mätningar vi kallar chroma ovan ( C eller C ₂ ).

Exempel

Alla parametervärden som visas nedan är angivna som värden i intervallet [0, 1] , förutom de för H och H ₂ , som ligger i intervallet [0°, 360°) .

Färg	R	G	B	H	H 2	C	C 2	V	L	jag	Y′ 601	S HSV	S HSL	S HSI
#FFFFFF	1 000	1 000	1 000	n/a	n/a	0,000	0,000	1 000	1 000	1 000	1 000	0,000	0,000	0,000
#808080	0,500	0,500	0,500	n/a	n/a	0,000	0,000	0,500	0,500	0,500	0,500	0,000	0,000	0,000
#000000	0,000	0,000	0,000	n/a	n/a	0,000	0,000	0,000	0,000	0,000	0,000	0,000	0,000	0,000
#FF0000	1 000	0,000	0,000	0,0 °	0,0 °	1 000	1 000	1 000	0,500	0,333	0,299	1 000	1 000	1 000
#BFBF00	0,750	0,750	0,000	60,0 °	60,0 °	0,750	0,750	0,750	0,375	0,500	0,664	1 000	1 000	1 000
#008000	0,000	0,500	0,000	120,0 °	120,0 °	0,500	0,500	0,500	0,250	0,167	0,293	1 000	1 000	1 000
#80FFFF	0,500	1 000	1 000	180,0 °	180,0 °	0,500	0,500	1 000	0,750	0,833	0,850	0,500	1 000	0,400
#8080FF	0,500	0,500	1 000	240,0 °	240,0 °	0,500	0,500	1 000	0,750	0,667	0,557	0,500	1 000	0,250
#BF40BF	0,750	0,250	0,750	300,0 °	300,0 °	0,500	0,500	0,750	0,500	0,583	0,457	0,667	0,500	0,571
#A0A424	0,628	0,643	0,142	61,8 °	61,5 °	0,501	0,494	0,643	0,393	0,471	0,581	0,779	0,638	0,699
#411BEA	0,255	0,104	0,918	251,1 °	250,0 °	0,814	0,750	0,918	0,511	0,426	0,242	0,887	0,832	0,756
#1EAC41	0,116	0,675	0,255	134,9 °	133,8 °	0,559	0,504	0,675	0,396	0,349	0,460	0,828	0,707	0,667
#F0C80E	0,941	0,785	0,053	49,5 °	50,5 °	0,888	0,821	0,941	0,497	0,593	0,748	0,944	0,893	0,911
#B430E5	0,704	0,187	0,897	283,7 °	284,8 °	0,710	0,636	0,897	0,542	0,596	0,423	0,792	0,775	0,686
#ED7651	0,931	0,463	0,316	14,3 °	13,2 °	0,615	0,556	0,931	0,624	0,570	0,586	0,661	0,817	0,446
#FEF888	0,998	0,974	0,532	56,9 °	57,4 °	0,466	0,454	0,998	0,765	0,835	0,931	0,467	0,991	0,363
#19CB97	0,099	0,795	0,591	162,4 °	163,4 °	0,696	0,620	0,795	0,447	0,495	0,564	0,875	0,779	0,800
#362698	0,211	0,149	0,597	248,3 °	247,3 °	0,448	0,420	0,597	0,373	0,319	0,219	0,750	0,601	0,533
#7E7EB8	0,495	0,493	0,721	240,5 °	240,4 °	0,228	0,227	0,721	0,607	0,570	0,520	0,316	0,290	0,135

Använd i slutanvändarprogramvara

Se även: Färgväljare och Bildredigering

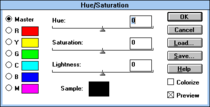
Fig 16a–g. På 1990-talet var HSL och HSV färgvalsverktyg överallt. Skärmbilderna ovan är tagna från: · (a) SGI IRIX 5, c. 1995; · (b) Adobe Photoshop , c. 1990; · (c) IBM OS/2 Warp 3, c. 1994; · (d) Apple Macintosh System 7 , c. 1996; · (e) Fractal Design Painter , c. 1993; · (f) Microsoft Windows 3.1 , c. 1992; · (g) NeXTSTEP , c. 1995. Dessa är utan tvekan baserade på tidigare exempel, som sträcker sig tillbaka till PARC och NYIT i mitten av 1970-talet.

Det ursprungliga syftet med HSL och HSV och liknande modeller, och deras vanligaste nuvarande tillämpning, är i färgvalsverktyg . Som enklast har vissa sådana färgväljare tre skjutreglage, en för varje attribut. De flesta visar dock ett tvådimensionellt snitt genom modellen, tillsammans med ett skjutreglage som styr vilken speciell skiva som visas. Den senare typen av GUI uppvisar stor variation, på grund av valet av cylindrar, hexagonala prismor eller koner/bicones som modellerna föreslår (se diagrammet längst upp på sidan ) . Flera färgväljare från 1990-talet visas till höger, varav de flesta har förblivit nästan oförändrade under den mellanliggande tiden: i dag använder nästan varje datorfärgväljare HSL eller HSV, åtminstone som ett alternativ. Vissa mer sofistikerade varianter är designade för att välja hela uppsättningar av färger, baserat sina förslag på kompatibla färger på HSL- eller HSV-relationerna mellan dem.

De flesta webbapplikationer som behöver färgval baserar också sina verktyg på HSL eller HSV, och förpackade färgväljare med öppen källkod finns för de flesta stora webbgränssnittsramverk . CSS 3- specifikationen tillåter webbförfattare att ange färger för sina sidor direkt med HSL-koordinater.

HSL och HSV används ibland för att definiera gradienter för datavisualisering , som i kartor eller medicinska bilder. Till exempel har det populära GIS -programmet ArcGIS historiskt tillämpat anpassningsbara HSV-baserade gradienter på numeriska geografiska data.

Fig. 17. xv :s HSV-baserade färgmodifierare.

Fig. 18. Nyans/mättnadsverktyget i Photoshop 2.5, ca. 1992.

Bildredigeringsprogram innehåller också vanligtvis verktyg för att justera färger med hänvisning till HSL- eller HSV-koordinater, eller till koordinater i en modell baserad på "intensiteten" eller luma som definieras ovan . I synnerhet verktyg med ett par "nyans" och "mättnad"-skjutreglage är vanliga, åtminstone från slutet av 1980-talet, men olika mer komplicerade färgverktyg har också implementerats. Unix bildvisare och färgredigerare xv tillät till exempel sex användardefinierbara färgtonsområden ( H ) att roteras och storleksändras, inklusive en rattliknande kontroll för mättnad ( S _HSV ) och ett kurvliknande gränssnitt för kontroll av värde ( V )—se fig. 17. Bildredigeraren Picture Window Pro inkluderar ett verktyg för "färgkorrigering" som ger komplex ommappning av punkter i ett nyans-/mättnadsplan relativt antingen HSL- eller HSV-rymden.

Videoredigerare använder också dessa modeller. Till exempel inkluderar både Avid och Final Cut Pro färgverktyg baserade på HSL eller en liknande geometri för att justera färgen i video. Med Avid-verktyget väljer användare en vektor genom att klicka på en punkt inom nyans-/mättnadscirkeln för att flytta alla färger på en viss ljushetsnivå (skuggor, mellantoner, högdagrar) efter den vektorn.

Sedan version 4.0 har Adobe Photoshops blandningslägen "Luminosity", "Hue", "Saturation" och "Color" sammansatta lager med hjälp av en luma/chroma/hue-färggeometri. Dessa har kopierats flitigt, men flera imitatorer använder HSL (t.ex. PhotoImpact , Paint Shop Pro ) eller HSV-geometrierna istället.

Använd i bildanalys

Se även: Datorseende och bildanalys

HSL, HSV, HSI eller relaterade modeller används ofta i datorseende och bildanalys för funktionsdetektering eller bildsegmentering . Tillämpningarna av sådana verktyg inkluderar objektdetektering, till exempel i robotseende ; objektigenkänning , till exempel av ansikten , text eller registreringsskyltar ; innehållsbaserad bildhämtning ; och analys av medicinska bilder .

För det mesta är datorseendealgoritmer som används på färgbilder enkla tillägg till algoritmer designade för gråskalebilder , till exempel k-medel eller suddig klustring av pixelfärger, eller kannykantdetektering . I det enklaste leds varje färgkomponent separat genom samma algoritm. Det är därför viktigt att de egenskaperna kan urskiljas i de färgdimensioner som används. Eftersom R , G och B -komponenterna i ett objekts färg i en digital bild alla är korrelerade med mängden ljus som träffar objektet, och därför med varandra, gör bildbeskrivningar i termer av dessa komponenter det svårt att skilja objekt åt. Beskrivningar i termer av nyans/ljushet/krom eller nyans/ljushet/mättnad är ofta mer relevanta.

Från och med slutet av 1970-talet användes transformationer som HSV eller HSI som en kompromiss mellan effektivitet för segmentering och beräkningskomplexitet. De kan betraktas som liknande tillvägagångssätt och avsikter med den neurala bearbetning som används av människans färgseende, utan att komma överens i detalj: om målet är objektdetektering, är grovt separering av nyans, ljushet och färg eller mättnad effektiv, men det finns ingen särskild anledning att strikt efterlikna mänskliga färgsvar. John Kenders magisteravhandling från 1976 föreslog HSI-modellen. Ohta et al. (1980) använde istället en modell uppbyggd av dimensioner liknande de vi har kallat I , α , och β . Under de senaste åren har sådana modeller fortsatt att se stor användning, eftersom deras prestanda jämförs med mer komplexa modeller, och deras enkelhet i beräkningen är fortfarande övertygande.

Nackdelar

Fig 20a. sRGB - omfånget kartlagt i CIELAB-rymden. Lägg märke till att linjerna som pekar mot de röda, gröna och blå primärerna inte är jämnt fördelade av nyansvinkeln och har olika längd. Primärerna har också olika L *-värden.

Fig 20b. Adobe RGB -omfånget kartlagt i CIELAB-rymden. Lägg också märke till att dessa två RGB-utrymmen har olika omfång och därför kommer att ha olika HSL- och HSV-representationer.

Även om HSL, HSV och relaterade utrymmen fungerar tillräckligt bra för att till exempel välja en enskild färg, ignorerar de mycket av komplexiteten i färgutseendet. I grund och botten byter de upp perceptuell relevans för beräkningshastighet, från en tid i datorhistorien (avancerade grafikarbetsstationer från 1970-talet eller mitten av 1990-talets konsumentdatorer) när mer sofistikerade modeller skulle ha varit för beräkningsmässigt dyra.

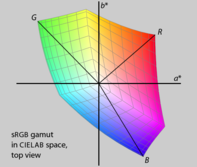
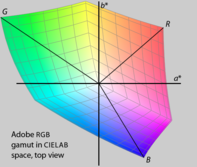
HSL och HSV är enkla transformationer av RGB som bevarar symmetrier i RGB-kuben som inte är relaterade till mänsklig perception, så att dess R , G och B -hörn är lika långt från den neutrala axeln och lika fördelade runt den. Om vi ​​plottar RGB-omfånget i ett mer perceptuellt enhetligt utrymme, som CIELAB (se nedan ), blir det omedelbart tydligt att de röda, gröna och blå primärerna inte har samma ljushet eller färg, eller jämnt fördelade nyanser. Dessutom använder olika RGB-skärmar olika primära skärmar och har därför olika omfång. Eftersom HSL och HSV definieras enbart med hänvisning till ett visst RGB-utrymme, är de inte absoluta färgrymder : för att specificera en färg exakt kräver rapportering inte bara HSL- eller HSV-värden, utan också egenskaperna hos RGB-utrymmet de är baserade på, inklusive gammakorrigering vid användning.

Om vi ​​tar en bild och extraherar komponenterna för nyans, mättnad och ljushet eller värde, och sedan jämför dessa med komponenterna med samma namn som definierats av färgforskare, kan vi snabbt se skillnaden, perceptuellt. Undersök till exempel följande bilder av en brandventilation ( fig. 13 ) . Originalet finns i sRGB-färgrymden. CIELAB L * är en CIE-definierad akromatisk ljushetskvantitet (beroende enbart på den perceptuella akromatiska luminansen Y , men inte de blandade kromatiska komponenterna X eller Z , i CIEXYZ-färgrymden från vilken själva sRGB-färgrymden härrör), och den är enkel att detta liknar den ursprungliga färgbilden i perceptuell ljushet. Luma är ungefär lika, men skiljer sig något vid hög kromaticitet, där den avviker mest från beroende enbart på den verkliga akromatiska luminansen ( Y , eller ekvivalent L *) och påverkas av den kolorimetriska kromaticiteten ( x,y , eller ekvivalent, a*, b* av CIELAB). HSL L och HSVV skiljer sig däremot väsentligt från perceptuell lätthet.

Fig. 13a. Färgfotografi (sRGB-färgrymd).

Fig. 13b. CIELAB L * (omvandlas ytterligare tillbaka till sRGB för konsekvent visning).

Fig. 13c. Rec. 601 luma Y' .

Fig. 13d. Komponentmedelvärde: "intensitet" I .

Fig. 13e. HSV-värde V .

Fig. 13f. HSL lätthet L .

    Även om ingen av dimensionerna i dessa utrymmen matchar deras perceptuella analoger, är värdet av HSV och mättnaden av HSL speciella brottslingar. I HSV hålls de blå primära och vita för att ha samma värde, även om perceptuellt den blå primära har någonstans runt 10 % av luminansen av vitt (den exakta andelen beror på de särskilda RGB-primärerna som används ) . I HSL hålls en blandning av 100 % rött, 100 % grönt, 90 % blått – det vill säga mycket ljusgult – ha samma mättnad som den gröna primärfärgen,   även om den förstnämnda färgen nästan inte har någon färg eller mättnad med de konventionella psykometriska definitionerna. Sådana perversiteter fick Cynthia Brewer, expert på färgschemaval för kartor och informationsskärmar, att berätta för American Statistical Association :

Datavetenskap erbjuder några fattigare kusiner till dessa perceptuella utrymmen som också kan dyka upp i ditt programvarugränssnitt, som HSV och HLS. De är enkla matematiska transformationer av RGB, och de verkar vara perceptuella system eftersom de använder sig av terminologin nyans-lätthet/värde-mättnad. Men ta en närmare titt; låt dig inte luras. Perceptuella färgdimensioner är dåligt skalade av färgspecifikationerna som tillhandahålls i dessa och vissa andra system. Till exempel förväxlas mättnad och ljushet, så en mättnadsskala kan också innehålla ett brett spektrum av ljusstyrkor (till exempel kan den gå från vitt till grönt, vilket är en kombination av både ljushet och mättnad). Likaså förväxlas nyans och ljushet så att till exempel en mättad gul och mättad blå kan betecknas som samma "ljushet" men har stora skillnader i upplevd ljushet. Dessa brister gör systemen svåra att använda för att kontrollera utseendet på ett färgschema på ett systematiskt sätt. Om mycket justeringar krävs för att uppnå önskad effekt, erbjuder systemet liten fördel jämfört med att brottas med råspecifikationer i RGB eller CMY.

     Om dessa problem gör HSL och HSV problematiska för att välja färger eller färgscheman, gör de dem mycket värre för bildjustering. HSL och HSV, som Brewer nämnde, förväxlar perceptuella färgskapande attribut, så att ändring av valfri dimension resulterar i olikformiga förändringar av alla tre perceptuella dimensioner och förvränger alla färgförhållanden i bilden. Om du till exempel roterar nyansen av en ren mörkblå mot grönt kommer också att minska dess upplevda färgning och öka dess upplevda ljushet (den senare är gråare och ljusare), men samma nyansrotation kommer att ha motsatt inverkan på ljusheten och färgningen av en ljusare blågrön— till (den senare är mer färgglad och något mörkare). I exemplet nedan ( fig. 21 ) är bilden till vänster (a) originalfotografiet av en grön sköldpadda . I mittenbilden (b) har vi roterat nyansen ( H ) för varje färg med -30° , samtidigt som HSV-värdet och mättnaden eller HSL-ljusheten och mättnaden hållits konstant. I bilden till höger (c) gör vi samma rotation till HSL/HSV-nyansen för varje färg, men sedan tvingar vi CIELAB-ljusheten ( L *, en anständig approximation av upplevd ljushet) att förbli konstant. Lägg märke till hur den nyansförskjutna mellanversionen utan en sådan korrigering dramatiskt förändrar de upplevda ljushetsförhållandena mellan färgerna i bilden. I synnerhet är sköldpaddans skal mycket mörkare och har mindre kontrast, och bakgrundsvattnet är mycket ljusare.

Fig. 21a. Färgfotografi.

Fig. 21b. HSL/HSV-nyans för varje färg förskjuten med -30° .

Fig. 21c. Nyansen ändrades men CIELABs ljushet ( L *) behölls som i originalet.

Eftersom nyans är en cirkulär storhet, representerad numeriskt med en diskontinuitet vid 360°, är den svår att använda i statistiska beräkningar eller kvantitativa jämförelser: analys kräver användning av cirkulär statistik . Dessutom definieras färgtonen bitvis, i 60°-bitar, där förhållandet mellan ljushet, värde och färgton till R , G och B beror på färgtonsbiten i fråga. Denna definition introducerar diskontinuiteter, hörn som tydligt kan ses i horisontella skivor av HSL eller HSV.

Charles Poynton, expert på digital video, listar ovanstående problem med HSL och HSV i sin Color FAQ och drar slutsatsen att:

HSB och HLS utvecklades för att specificera numerisk nyans, mättnad och ljusstyrka (eller nyans, ljushet och mättnad) i en tid då användare var tvungna att ange färger numeriskt. De vanliga formuleringarna av HSB och HLS är felaktiga med avseende på egenskaperna hos färgseende. Nu när användare kan välja färger visuellt, eller välja färger relaterade till andra media (som PANTONE ), eller använda perceptuellt baserade system som L*u*v* och L*a*b* , bör HSB och HLS överges.

Andra färgmodeller med cylindrisk koordinat

Huvudartiklar: Färgmodell § Cylindriska koordinatfärgmodeller och Lista över färgrymder och deras användning § Cylindriska transformationer

Skaparna av HSL och HSV var långt ifrån de första att föreställa sig färger som passade in i koniska eller sfäriska former, med neutrala färger som löper från svart till vitt i en central axel, och nyanser som motsvarar vinklar runt den axeln. Liknande arrangemang går tillbaka till 1700-talet och fortsätter att utvecklas i de modernaste och mest vetenskapliga modellerna.

Formler för färgkonvertering

För att konvertera från HSL eller HSV till RGB, inverterar vi i huvudsak stegen som anges ovan (som tidigare, R , G , B ∈ [0, 1] ) . Först beräknar vi chroma, genom att multiplicera mättnad med den maximala chroma för en given ljushet eller ett givet värde. Därefter hittar vi punkten på en av de tre nedre ytorna av RGB-kuben som har samma nyans och färg som vår färg (och därför projicerar på samma punkt i färgplanet). Slutligen lägger vi till lika stora mängder R , G och B för att nå rätt ljushet eller värde.

Till RGB

HSL till RGB

Givet en färg med nyans H ∈ [0°, 360°] , mättnad S _L ∈ [0, 1] och ljushet L ∈ [0, 1] finner vi först chroma:

$C=(1-\left\vert 2L-1\right\vert )\ gånger S_{L}$

Sedan kan vi hitta en punkt ( R ₁ , G ₁ , B ₁ ) längs de tre nedre ytorna av RGB-kuben, med samma nyans och kroma som vår färg (med mellanvärdet X för den näst största komponenten i denna färg) :

$H^{\prime }={\frac {H}{60^{\circ }}}$

${\ displaystyle X=C\times (1-|H^{\prime }\;{\bmod {2}}-1|)}$

I ekvationen ovan hänvisar notationen $H^{\prime }\;{\bmod {2}}$ till resten av den euklidiska divisionen av $H^{\prime }$ med 2. $H^{\prime }$ är inte nödvändigtvis ett heltal.

$(R_{1},G_{ 1},B_{1})={\begin{cases}(C,X,0)&{\text{if }}0\leq H^{\prime }<1\\(X,C,0) &{\text{if }}1\leq H^{\prime }<2\\(0,C,X)&{\text{if }}2\leq H^{\prime }<3\\( 0,X,C)&{\text{if }}3\leq H^{\prime }<4\\(X,0,C)&{\text{if }}4\leq H^{\prime <5\\(C,0,X)&{\text{if }}5\leq H^{\prime }<6\end{cases}}$

När $H^{\prime }$ är ett heltal, skulle "grannformeln" ge samma resultat, eftersom $X=0$ eller $X=C$ , som lämpligt.

Slutligen kan vi hitta R , G och B genom att lägga till samma mängd till varje komponent, för att matcha lätthet:

$m=L-{\frac {C}{2}}$

${\ displaystil (R,G,B)=(R_{1}+m,G_{1}+m,B_{1}+m)}$

HSL till RGB alternativ

De polygonala styckvisa funktionerna kan förenklas något genom smart användning av minimi- och maximivärden samt resten av operationen.

Givet en färg med nyans $H\in [0^{\circ },360^{\circ }]$ , mättnad $S =S_{L}\in [0,1]$ , och ljushet $L\in [0,1]$ , definierar vi först funktionen:

$f(n)=La\max(-1,\min(k-3,9- k,1))$

där $k,n\in \mathbb {R} _{\geq 0}$ och:

$k=(n+{\frac {H}{30^{\circ }}}){\bmod {1}}2$

$a=S_{L}\min(L,1-L)$

Och utmatade R,G,B-värden (från ${\displaystyle [0,1]^{3}} )$ är:

$(R,G,B)=(f(0),f(8),f(4))$

Ovanstående alternativa formler tillåter kortare implementeringar. I formlerna ovan $a{\bmod {b}}$ också bråkdelen av modulen, t.ex. $7.4{\bmod {6}}=1.4$ , och $k\in [0,12)$ .

Basformen $T(k)=t(n,H)=\max (\min(k-3,9-k,1),-1)$ konstrueras enligt följande: $t_{1}=\min(k- 3,9-k)$ är en "triangel" för vilken värden större eller lika med −1 börjar från k=2 och slutar vid k=10, och den högsta punkten är vid k=6. Sedan med $t_{2}=\min(t_{1},1)=\min(k-3 ,9-k,1)$ ändrar vi värden större än 1 till lika med 1. Sedan ändrar vi värden med $t=\max(t_{2},-1)$ mindre än −1 till lika med −1. Vid det här laget får vi något som liknar den röda formen från fig. 24 efter en vertikal vändning (där maximum är 1 och minimum är -1). R,G,B-funktionerna i $H$ använder denna form transformerad på följande sätt: modulo-skiftad på $X$ (med $n$ ) (på annat sätt för R,G,B ) skalas på $Y$ (med $-a$ ) och skiftas på $Y$ (med $L$ ).

Vi observerar följande formegenskaper (fig. 24 kan hjälpa till att få en intuition om dem):

$t(n,H)=-t(n+6,H)$

$\min \ (t(n,H),t(n+4,H),t(n+8,H))=- 1$

$\max \ (t(n,H),t(n+ 4,H),t(n+8,H))=+1$

HSV till RGB

Fig. 24. En grafisk representation av RGB-koordinater givna värden för HSV. Denna ekvation $V(1-S)=V-VS$ visar ursprunget för markerade vertikala axelvärden

Givet en HSV-färg med nyans H ∈ [0°, 360°] , mättnad _kan SV ∈ [0, 1] och värdet V ∈ [0, 1] vi använda samma strategi. Först hittar vi chroma:

$C=V\times S_{V}$

Sedan kan vi återigen hitta en punkt ( R ₁ , G ₁ , B ₁ ) längs de tre nedre ytorna av RGB-kuben, med samma nyans och färgton som vår färg (med hjälp av mellanvärdet X för den näst största komponenten av denna färg):

$H^{\prime }={\frac {H}{60^{\circ }}}$

${\ displaystil X=C\ gånger (1-|H^{\prime }{\bmod {2}}-1|)}$

$(R_{1},G_{1},B_{1})={\begin{cases}(C,X,0) &{\text{if }}0\leq H^{\prime }<1\\(X,C,0)&{\text{if }}1\leq H^{\prime }<2\\( 0,C,X)&{\text{if }}2\leq H^{\prime }<3\\(0,X,C)&{\text{if }}3\leq H^{\prime <4\\(X,0,C)&{\text{if }}4\leq H^{\prime }<5\\(C,0,X)&{\text{if }}5\ leq H^{\prime }<6\end{cases}}$

Som tidigare, när $H^{\prime }$ är ett heltal, skulle "angränsande" formler ge samma resultat.

Slutligen kan vi hitta R , G och B genom att lägga till samma mängd till varje komponent, för att matcha värdet:

$m=VC$

$(R,G,B)=(R_{ 1}+m,G_{1}+m,B_{1}+m)$

HSV till RGB alternativ

Givet en färg med nyans $H\in [0^{\circ },360^{\circ }]$$S =S_{V}\in [0,1]$ mättnad , och värdet $V\in [0,1]$ , först definierar vi funktion :

$f(n)=V-VS\max(0,\min(k,4-k,1) )$

där $k,n\in \mathbb {R} _{\geq 0}$ och:

$k=(n+{\frac {H}{60^{\circ }}}){\bmod {6}}$

Och utmatade R,G,B-värden (från ${\displaystyle [0,1]^{3}} )$ är:

$(R,G,B)=(f(5),f(3),f(1) )$

Ovan alternativa ekvivalenta formler tillåter kortare implementering. I ovanstående formler $a{\bmod {b}}$ också en del av modulen, t.ex. formeln $7.4{\bmod {6}}=1.4$ . Värdena för $k\in \mathbb {R} \land k\in [0,6)$ . Basformen

$t(n,H)=T(k)=\max(0,\min(k) ,4-k,1))$

är konstruerad enligt följande: $t_{1}=\min(k,4-k)$ är "triangel" för vilken icke-negativa värden börjar från k=0, högsta punkten vid k=2 och "slutar" vid k=4, då ändrar vi värden större än ett till ett med ${\displaystyle t_ {2}=\min(t_{1},1)=\min(k,4-k,1)} ,$ ändra sedan negativa värden till noll med $t=\max (t2,0)$ – och vi får (för $n=0$ ) något som liknar grön form från Fig. 24 (vilket maxvärde är 1 och minvärde är 0). R,G,B-funktionerna för $H$ använder denna form transformerad på följande sätt: modulo-skiftad på $X$ (med $n$ ) (på annat sätt för R,G,B) skalas på $Y$ (med $-VS$ ) och skiftas på $Y$ (med $V$ ). Vi observerar följande formegenskaper (fig. 24 kan hjälpa till att få intuition om detta):

$t(n,H)=1-t(n+3,H)$

$\min(t(n,H),t(n+2,H),t(n+4,H))=0$

$\max(t(n,H),t(n+2,H) ,t(n+4,H))=1$

HSI till RGB

Givet en HSI-färg med nyans H ∈ [0°, 360°] , mättnad S _I ∈ [0, 1] och intensitet I ∈ [0, 1] , kan vi använda samma strategi, i en något annan ordning:

$H^{\prime }={\frac {H}{60^{\circ }}}$

$Z=1-|H^{\prime }\;{\bmod {2}}-1|$

$C={\frac {3\cdot I\cdot S_{I}}{1+Z}}$

$X=C\cdot Z$

Där $C$ är chroma.

Sedan kan vi återigen hitta en punkt ( R ₁ , G ₁ , B ₁ ) längs de tre nedre ytorna av RGB-kuben, med samma nyans och färgton som vår färg (med hjälp av mellanvärdet X för den näst största komponenten av denna färg):

$\ stil$

Överlappning (när $H^{\prime }$ är ett heltal) uppstår eftersom två sätt att beräkna värdet är ekvivalenta: $X=0$ eller $X=C$ , efter behov.

Slutligen kan vi hitta R , G och B genom att lägga till samma mängd till varje komponent, för att matcha lätthet:

$m=I\cdot (1-S_{I})$

$(R,G,B)=(R_{1}+m,G_{1}+m,B_{1}+m)$

Luma, chroma och nyans till RGB

Givet en färg med nyans H ∈ [0°, 360°) , chroma C ∈ [0, 1] och luma Y ′ ₆₀₁ ∈ [0, 1] , kan vi återigen använda samma strategi. Eftersom vi redan har H och C , kan vi genast hitta vår punkt ( R ₁ , G ₁ , B ₁ ) längs de tre nedre ytorna av RGB-kuben:

${\begin{aligned}H^{\prime }&={\frac {H}{60^{\ circ }}}\\X&=C\times (1-|H^{\prime }{\bmod {2}}-1|)\end{aligned}}$

$(R_{1},G_{1}, B_{1})={\begin{cases}(0,0,0)&{\text{om }}H{\text{ är odefinierad}}\\(C,X,0)&{\text{ om }}0\leq H^{\prime }\leq 1\\(X,C,0)&{\text{if }}1\leq H^{\prime }\leq 2\\(0,C ,X)&{\text{if }}2\leq H^{\prime }\leq 3\\(0,X,C)&{\text{if }}3\leq H^{\prime }\ leq 4\\(X,0,C)&{\text{if }}4\leq H^{\prime }\leq 5\\(C,0,X)&{\text{if }}5\ leq H^{\prime }<6\end{cases}}$

Överlappning (när $H^{\prime }$ är ett heltal) uppstår eftersom två sätt att beräkna värdet är ekvivalenta: $X=0$ eller $X=C$ , efter behov.

Sedan kan vi hitta R , G och B genom att lägga till samma mängd till varje komponent, för att matcha luma:

$m=Y_{601}^{\prime }-(0.30R_{1}+0.59G_{1}+0.11B_{ 1})$

$(R,G,B)=(R_{1}+m,G_{1 }+m,B_{1}+m)$

Interkonvertering

HSV till HSL

Givet en färg med nyans ${\displaystyle H_{V}\in [0^{\circ },360^{\circ }]} ,$$\ displaystyle S_{V}\in [0,1]}$ SV , och värdet $V\in [0,1]$ ,

$H_{L}=H_{V}$

$=V\left(1-{\frac {S_{V}}{2 }}\right)}$

$S_{L}={\begin{cases}0&{\text{if } }L=0{\text{ eller }}L=1\\{\frac {VL}{\min(L,1-L)}}&{\text{annars}}\\\end{case}}$

HSL till HSV

Givet en färg med nyans ${\displaystyle H_{L}\in [0^{\circ },360^{\circ }]} ,$ mättnad ${\ displaystyle S_{L}\in [0,1]}$ , och luminans $L\in [0,1]$ ,

$H_{V}=H_{L}$

$V=L+S_{L}\min(L,1- L)$

$S_{V}={\begin{cases}0&{\text{if }}V=0\\2\left(1) -{\frac {L}{V}}\right)&{\text{annars}}\\\end{case}}$

Från RGB

Se även: § Allmänt tillvägagångssätt

Detta är en upprepning av den tidigare konverteringen.

Värdet måste ligga inom området $R,G,B\in [0,1]$ .

Med maximal komponent (dvs värde)

$X_{max}:=\max(R,G,B)=:V$

och minimikomponent

$X_{min}:=\min(R,G,B)=VC$ ,

intervall (dvs. chroma)

$C:=X_{max}-X_{min}=2(VL)$

och mellanregister (dvs. lätthet)

$L:=\operatörsnamn {mid} (R,G,B)={\frac {X_{max}+X_{min}}{2}}=V-{\frac {C}{2}}$ ,

vi får gemensam nyans:

$H:={\begin{cases}0,&{\text{if }}C=0\\60^{\circ }\cdot \left({\frac {GB} {C}}\mod 6\right),&{\text{if }}V=R\\60^{\circ }\cdot \left({\frac {BR}{C}}+2\right) ,&{\text{if }}V=G\\60^{\circ }\cdot \left({\frac {RG}{C}}+4\right),&{\text{if }}V =B\end{cases}}$

och distinkta mättningar:

$S_{V}:={\begin{cases}0,&{\text{if }}V=0\\{\frac {C}{ V}},&{\text{annars}}\end{fall}}$

$S_{L}:={\begin{cases}0,&{\text{if }}L=0{\text{ eller }}L =1\\{\frac {C}{1-\left\vert 2V-C-1\right\vert }}={\frac {2(VL)}{1-\left\vert 2L-1\right \vert }}={\frac {VL}{\min(L,1-L)}},&{\text{annars}}\end{fall}}$

Swatches

För muspekaren över färgrutorna nedan för att se R- , G- och B -värdena för varje färgruta i ett verktygstips .

HSL

H = 180° H = 0° L \ S 1 3⁄4 _ _ 1⁄2 _ _ 1⁄4 _ _ 0 1⁄4 _ _ 1⁄2 _ _ 3⁄4 _ _ 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0	H = 210° H = 30° L \ S 1 3⁄4 _ _ 1⁄2 _ _ 1⁄4 _ _ 0 1⁄4 _ _ 1⁄2 _ _ 3⁄4 _ _ 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0
H = 240° H = 60° L \ S 1 3⁄4 _ _ 1⁄2 _ _ 1⁄4 _ _ 0 1⁄4 _ _ 1⁄2 _ _ 3⁄4 _ _ 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0	H = 270° H = 90° L \ S 1 3⁄4 _ _ 1⁄2 _ _ 1⁄4 _ _ 0 1⁄4 _ _ 1⁄2 _ _ 3⁄4 _ _ 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0
H = 300° H = 120° L \ S 1 3⁄4 _ _ 1⁄2 _ _ 1⁄4 _ _ 0 1⁄4 _ _ 1⁄2 _ _ 3⁄4 _ _ 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0	H = 330° H = 150° L \ S 1 3⁄4 _ _ 1⁄2 _ _ 1⁄4 _ _ 0 1⁄4 _ _ 1⁄2 _ _ 3⁄4 _ _ 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0

HSV

H = 180° H = 0° V \ S 1 3⁄4 _ _ 1⁄2 _ _ 1⁄4 _ _ 0 1⁄4 _ _ 1⁄2 _ _ 3⁄4 _ _ 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0	H = 210° H = 30° V \ S 1 3⁄4 _ _ 1⁄2 _ _ 1⁄4 _ _ 0 1⁄4 _ _ 1⁄2 _ _ 3⁄4 _ _ 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0
H = 240° H = 60° V \ S 1 3⁄4 _ _ 1⁄2 _ _ 1⁄4 _ _ 0 1⁄4 _ _ 1⁄2 _ _ 3⁄4 _ _ 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0	H = 270° H = 90° V \ S 1 3⁄4 _ _ 1⁄2 _ _ 1⁄4 _ _ 0 1⁄4 _ _ 1⁄2 _ _ 3⁄4 _ _ 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0
H = 300° H = 120° V \ S 1 3⁄4 _ _ 1⁄2 _ _ 1⁄4 _ _ 0 1⁄4 _ _ 1⁄2 _ _ 3⁄4 _ _ 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0	H = 330° H = 150° V \ S 1 3⁄4 _ _ 1⁄2 _ _ 1⁄4 _ _ 0 1⁄4 _ _ 1⁄2 _ _ 3⁄4 _ _ 1 1                   7 ⁄ 8                   3 ⁄ 4                   5 ⁄ 8                   1 ⁄ 2                   3 ⁄ 8                   1 ⁄ 4                   1 ⁄ 8                   0

Se även

• TSL färgrymd

Bibliografi

•   Agoston, Max K. (2005). Datorgrafik och geometrisk modellering: Implementering och algoritmer . London: Springer. s. 300–306. ISBN 978-1-85233-818-3 . Agostons bok innehåller en beskrivning av HSV och HSL, och algoritmer i pseudokod för konvertering till var och en från RGB och tillbaka igen.
•   Cheng, Heng-Da; Jiang, Xihua; Sun, Angela; Wang, Jingli (2001). "Färgbildssegmentering: Framsteg och framtidsutsikter". Mönsterigenkänning . 34 (12): 2259. CiteSeerX 10.1.1.119.2886 . doi : 10.1016/S0031-3203(00)00149-7 . Denna litteraturöversikt över datorseende sammanfattar kort forskning inom färgbildssegmentering, inklusive den som använder HSV- och HSI-representationer.
• Fairchild, Mark D. (2005). Färgutseendemodeller (2:a upplagan). Addison-Wesley. Den här boken diskuterar inte HSL eller HSV specifikt, men är en av de mest läsbara och exakta resurserna om aktuell färgvetenskap.
•   Foley, JD ; et al. (1995). Computer Graphics: Principles and Practice (2nd ed.). Redwood City, Kalifornien: Addison-Wesley. ISBN 978-0-201-84840-3 . Standardläroboken för datorgrafik från 1990-talet, den här boken har ett kapitel fullt av algoritmer för konvertering mellan färgmodeller, i C .
• Hanbury, Allan; Serra, Jean (december 2002). En 3D-polär koordinatfärgrepresentation som lämpar sig för bildanalys . Mönsterigenkänning och bildbehandlingsgrupp Teknisk rapport 77 . Wien, Österrike: Wiens tekniska universitet.
•   Hanbury, Allan (2008). "Konstruera cylindriska koordinatfärgrymder" (PDF) . Mönsterigenkänningsbokstäver . 29 (4): 494–500. CiteSeerX 10.1.1.211.6425 . doi : 10.1016/j.patrec.2007.11.002 .
• Joblove, George H.; Greenberg, Donald (augusti 1978). "Färgutrymmen för datorgrafik" (PDF) . Datorgrafik . 12 (3): 20–25. doi : 10.1145/965139.807362 . Joblove och Greenbergs tidning var den första som beskrev HSL-modellen, som den jämför med HSV.
•   Kuehni, Rolf G. (2003). Färgrymd och dess indelningar: Färgordning från antiken till nutid . New York: Wiley. ISBN 978-0-471-32670-0 . Denna bok nämner bara kortfattat HSL och HSV, men är en omfattande beskrivning av färgordningssystem genom historien.
• Levkowitz, Haim; Herman, Gabor T. (1993). "GLHS: En generaliserad modell för ljushet, nyans och mättnadsfärg". CVGIP: Grafiska modeller och bildbehandling . 55 (4): 271–285. doi : 10.1006/cgip.1993.1019 . Denna artikel förklarar hur både HSL och HSV, såväl som andra liknande modeller, kan ses som specifika varianter av en mer allmän "GLHS"-modell. Levkowitz och Herman tillhandahåller pseudokod för konvertering från RGB till GLHS och tillbaka.
• MacEvoy, Bruce (januari 2010). "Färgsyn" . handprint.com . . Speciellt avsnitten om "Modern Color Models" och "Modern Color Theory" . MacEvoys omfattande sida om färgvetenskap och färgblandning är en av de bästa resurserna på webben. På den här sidan förklarar han färgtillverkningsattributen och de allmänna målen och historien för färgordningssystem – inklusive HSL och HSV – och deras praktiska relevans för målare.
• Poynton, Charles (1997). "Vanliga frågor om färg" . poynton.com . Denna självpublicerade sida med vanliga frågor, av digitalvideoexperten Charles Poynton, förklarar bland annat varför enligt hans åsikt dessa modeller "är värdelösa för att specificera exakt färg", och bör överges till förmån för mer psykometriskt relevanta modeller .
• Poynton, Charles (2008). " YUV och luminans anses vara skadligt" . poynton.com . Hämtad 30 augusti 2017 .
• Smith, Alvy Ray (augusti 1978). "Färgomfångstransformationspar" . Datorgrafik . 12 (3): 12–19. doi : 10.1145/965139.807361 . Detta är originalpapperet som beskriver "hexcone"-modellen, HSV. Smith var forskare vid NYIT :s Computer Graphics Lab. Han beskriver HSV:s användning i ett tidigt digitalt målningsprogram .

externa länkar

• Demonstrativ färgkonverteringsapplet
• HSV Colors av Hector Zenil, The Wolfram Demonstrations Project .
• HSV till RGB av CodeBeautify.