Förväntat värde inklusive osäkerhet

I beslutsteori och kvantitativ policyanalys är det förväntade värdet av att inkludera osäkerhet ( EVIU ) den förväntade skillnaden i värdet av ett beslut baserat på en probabilistisk analys kontra ett beslut baserat på en analys som ignorerar osäkerhet .

Bakgrund

Beslut måste fattas varje dag i den allestädes närvarande närvaron av osäkerhet. För de flesta dagliga beslut används olika heuristik för att agera rimligt i närvaro av osäkerhet, ofta med lite eftertanke om dess närvaro. Men för större beslut med hög insats eller beslut i mycket offentliga situationer kan beslutsfattare ofta dra nytta av en mer systematisk behandling av sina beslutsproblem, till exempel genom kvantitativ analys eller beslutsanalys .

När man bygger en kvantitativ beslutsmodell identifierar en modellbyggare olika relevanta faktorer och kodar dessa som indatavariabler . Från dessa indata kan andra kvantiteter, kallade resultatvariabler , beräknas; dessa ger information till beslutsfattaren. Till exempel, i exemplet som beskrivs nedan, måste beslutsfattaren bestämma hur snart innan ett flygs schemalagda avgång han måste lämna till flygplatsen (beslutet). En indatavariabel är hur lång tid det tar att köra till flygplatsens parkeringsgarage. Utifrån denna och andra indata kan modellen beräkna hur troligt det är att beslutsfattaren kommer att missa flygningen och vad nettokostnaden (i minuter) blir för olika beslut.

För att fatta ett beslut är en mycket vanlig praxis att ignorera osäkerhet. Beslut fattas genom kvantitativ analys och modellbygge genom att helt enkelt använda en bästa gissning (enkelt värde) för varje ingångsvariabel. Beslut fattas sedan om beräknade punktskattningar . I många fall kan dock ignorering av osäkerhet leda till mycket dåliga beslut, med uppskattningar för resultatvariabler som ofta vilseleder beslutsfattaren

Ett alternativ till att ignorera osäkerhet i kvantitativa beslutsmodeller är att uttryckligen koda in osäkerhet som en del av modellen. Med detta tillvägagångssätt tillhandahålls en sannolikhetsfördelning för varje indatavariabel, snarare än en enda bästa gissning. Variansen i den fördelningen speglar graden av subjektiv osäkerhet (eller brist på kunskap ) i insatskvantiteten. Mjukvaruverktygen använder sedan metoder som Monte Carlo-analys för att sprida osäkerheten till resultatvariabler, så att en beslutsfattare får en explicit bild av vilken inverkan osäkerheten har på hans beslut, och i många fall kan fatta ett mycket bättre beslut som en resultat.

När man jämför de två tillvägagångssätten – att explicit ignorera osäkerhet kontra modellering av osäkerhet – är den naturliga frågan att ställa sig hur stor skillnad det verkligen gör för kvaliteten på de beslut som fattas. På 1960-talet Ronald A. Howard ett sådant mått, det förväntade värdet av perfekt information (EVPI), ett mått på hur mycket det skulle vara värt att lära sig de "sanna" värdena för alla osäkra indatavariabler. Även om det ger ett mycket användbart mått på känslighet för osäkerhet, fångar EVPI inte direkt den faktiska förbättringen av beslut som erhållits genom att explicit representera och resonera om osäkerhet. För detta har Max Henrion, i sin Ph.D. avhandling, introducerade det förväntade värdet av inklusive osäkerhet (EVIU), ämnet för denna artikel.

Formalisering

Låta

${ \displaystyle {\begin{array}{ll}d\in D&{\text{beslutet som fattas, valt från mellanslag }}D\\x\i X&{\text{den osäkra kvantiteten, med sant värde i rymden } }X\\U(d,x)&{\text{verktygsfunktionen}}\\f(x)&{\text{den tidigare subjektiva sannolikhetsfördelningen (densitetsfunktionen) på }}x\end{array}} }$

När osäkerhet inte inkluderar, hittas det optimala beslutet med endast ${\displaystyle E[x]} ,$ det förväntade värdet för den osäkra kvantiteten. Beslutet som ignorerar osäkerhet ges därför av:

$d_{iu}={\arg \max _{d}}~U(d,E[x]).$

Det optimala beslutet med hänsyn till osäkerhet är Bayes standardbeslut som maximerar förväntad nytta :

$d^{*}={\arg \max _{d}}{\int U(d,x)f(x)\,dx}.$

EVIU är skillnaden i förväntad användbarhet mellan dessa två beslut:

$EVIU=\int _{X}\left[U(d^{*},x)-U(d_{iu},x)\right]f(x)\,dx.$

Den osäkra kvantiteten x och beslutsvariabeln d kan var och en vara sammansatt av många skalära variabler, i vilket fall utrymmena X och D var och en är vektorrum.

Exempel

[påverkansdiagram av EVIU-modell

Diagrammet till höger är ett influensdiagram för att bestämma hur tidigt beslutsfattaren ska lämna hemmet för att hinna med ett flyg på flygplatsen. Det enda beslutet, i den gröna rektangeln, är antalet minuter som man kommer att besluta sig för att lämna före planets avgångstid. Fyra osäkra variabler visas på diagrammet i cyanovaler: Tiden det tar att köra hemifrån till flygplatsens parkeringsgarage (i minuter), tid att ta sig från parkeringshuset till porten (i minuter), tiden före avgång som man måste vara vid gate, och förlusten (i minuter) som uppstår om flygningen missas. Var och en av dessa noder innehåller en sannolikhetsfördelning, nämligen:

 Time_to_drive_to_airport :=  LogNormal  (median:60,gsdev:1.3) Time_from_parking_to_gate :=  LogNormal  (median:10,gsdev:1.3) Gate_time_before_departure :=  Triangulär  (min:20,mode:30,median_max:40) Log_max  :  40 400,stddev:100) 

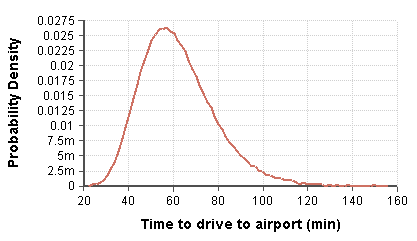
Var och en av dessa fördelningar anses vara statistiskt oberoende . Sannolikhetsfördelningen för den första osäkra variabeln, Time_to_drive_to_airport , med median 60 och en geometrisk standardavvikelse på 1,3, visas i denna graf:

Modellen beräknar kostnaden (den röda hexagonala variabeln) som antalet minuter (eller minutekvivalenter) som förbrukats för att framgångsrikt gå ombord på planet. Om man kommer för sent kommer man att missa sitt plan och dra på sig den stora förlusten (negativ nytta) att behöva vänta på nästa flyg. Om man anländer för tidigt, får man kostnaden för en onödigt lång väntan på flyget.

Modeller som använder EVIU kan använda en hjälpfunktion , eller på motsvarande sätt kan de använda en förlustfunktion , i vilket fall nyttofunktionen bara är det negativa av förlustfunktionen . I båda fallen kommer EVIU att vara positiv. Den största skillnaden är bara att med en förlustfunktion fattas beslutet genom att minimera förlusten snarare än genom att maximera användbarheten. I exemplet här används en förlustfunktion , Cost.

Definitionerna för var och en av de beräknade variablerna är således:

 Time_from_home_to_gate := Time_to_drive_to_airport + Time_from_parking_to_gate + Loss_if_miss_the_plane Value_per_minute_at_home := 1 

 Kostnad := Value_per_minute_at_home * Time_I_leave_home + (If Time_the_home Time_to_leavefrom annars 0) 

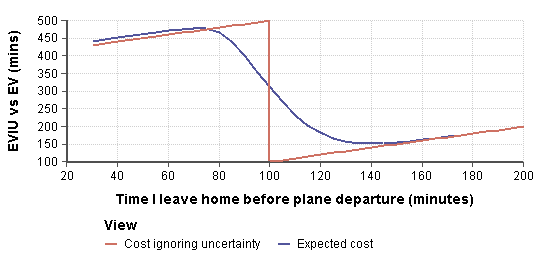
Följande graf visar det förväntade värdet med hänsyn till osäkerheten (den jämna blå kurvan) till den förväntade nyttan som ignorerar osäkerhet, ritat som en funktion av beslutsvariabeln.

När osäkerhet ignoreras agerar man som om flygningen kommer att göras med säkerhet så länge man går minst 100 minuter före flygningen, och kommer att missa flygningen med säkerhet om man åker senare än så. Eftersom man agerar som om allt är säkert är den optimala åtgärden att lämna exakt 100 minuter (eller 100 minuter, 1 sekund) före flygningen.

När osäkerheten beaktas jämnar det förväntade värdet ut (den blå kurvan), och den optimala åtgärden är att lämna 140 minuter före flygningen. Förväntningsvärdekurvan, med ett beslut 100 minuter före flygningen, visar den förväntade kostnaden när man bortser från osäkerhet till 313,7 minuter, medan den förväntade kostnaden när man åker 140 minuter före flygningen är 151 minuter. Skillnaden mellan dessa två är EVIU:

$EVIU=313.7-151=162.7{\text{ minuter}}$

Med andra ord, om osäkerheten uttryckligen beaktas när beslutet fattas, kommer en genomsnittlig besparing på 162,7 minuter att realiseras.

Linjär-kvadratisk kontroll

I samband med centraliserad linjär-kvadratisk styrning , med additiv osäkerhet i ekvationen för evolution men ingen osäkerhet om koefficientvärden i den ekvationen, är den optimala lösningen för kontrollvariablerna med hänsyn till osäkerheten densamma som att lösningen ignorerar osäkerhet. Denna egenskap, som ger ett förväntat värde på noll för att inkludera osäkerhet, kallas säkerhetekvivalens .

Relation till förväntat värde av perfekt information (EVPI)

Både EVIU och EVPI jämför det förväntade värdet av Bayes beslut med ett annat beslut som fattats utan osäkerhet. För EVIU fattas detta andra beslut när osäkerheten ignoreras , även om den finns där, medan för EVPI fattas detta andra beslut efter att osäkerheten har tagits bort genom att få perfekt information om x .

EVPI är den förväntade kostnaden för att vara osäker på x , medan EVIU är den förväntade extra kostnaden för att anta att man är säker .

EVIU, liksom EVPI, ger förväntat värde i termer av enheterna för hjälpfunktionen.

Se även

• Förväntat värde av exempelinformation
• Bulksändning förfaller