Ekvivalenta impedanstransformationer
| Linjär nätverksanalys | |
|---|---|
| Element | |
| Komponenter | |
| Serie- och parallellkretsar | |
| Impedanstransformationer | |
| Generatorsatser | Nätverkssatser _ |
| Nätverksanalysmetoder | |
| Tvåportsparametrar | |
En ekvivalent impedans är en ekvivalent krets av ett elektriskt nätverk av impedanselement som uppvisar samma impedans mellan alla par av terminaler som det givna nätverket gjorde. Den här artikeln beskriver matematiska transformationer mellan några passiva , linjära impedansnätverk som vanligtvis finns i elektroniska kretsar.
Det finns ett antal mycket välkända och ofta använda ekvivalenta kretsar inom linjär nätverksanalys . Dessa inkluderar motstånd i serie , resistorer i parallell och utbyggnaden till serie- och parallellkretsar för kondensatorer , induktorer och allmänna impedanser. Också välkända är Norton- och Thévenins ekvivalenta strömgenerator- och spänningsgeneratorkretsar, liksom Y-A-transformen . Inget av dessa diskuteras i detalj här; de enskilda länkade artiklarna bör konsulteras.
Antalet ekvivalenta kretsar som ett linjärt nätverk kan omvandlas till är obegränsat. Även i de mest triviala fallen kan detta ses vara sant, till exempel genom att fråga hur många olika kombinationer av motstånd parallellt som motsvarar ett givet kombinerat motstånd. Antalet serie- och parallellkombinationer som kan bildas växer exponentiellt med antalet motstånd, n . För stora n har storleken på uppsättningen med numeriska tekniker befunnits vara ungefär 2,53 n och analytiskt strikta gränser ges av en Farey-sekvens av Fibonacci-tal . Den här artikeln skulle aldrig kunna hoppas på att bli heltäckande, men det finns några generaliseringar möjliga. Wilhelm Cauer hittade en transformation som kunde generera alla möjliga ekvivalenter av en given rationell, passiv, linjär enport , eller med andra ord, vilken som helst given tvåterminalsimpedans. Transformationer av 4-terminals, speciellt 2-ports, nätverk är också vanligt förekommande och transformationer av ännu mer komplexa nätverk är möjliga.
Den stora omfattningen av ämnet motsvarande kretsar understryks i en berättelse berättad av Sidney Darlington . Enligt Darlington hittades ett stort antal likvärdiga kretsar av Ronald M. Foster , efter hans och George Campbells papper från 1920 om icke-dissipativa fyra-portar. Under arbetets gång tittade de på hur fyra portar kunde kopplas samman med idealiska transformatorer och maximal kraftöverföring. De hittade ett antal kombinationer som kan ha praktiska tillämpningar och bad AT&T patentavdelning att få dem patenterade. Patentavdelningen svarade att det var meningslöst att bara patentera några av kretsarna om en konkurrent kunde använda en likvärdig krets för att komma runt patentet; de borde patentera alla eller inte bry sig. Foster började därför arbeta med att beräkna varenda en av dem. Han kom fram till en enorm summa på 83 539 ekvivalenter (577 722 om olika produktionskvoter ingår). Detta var för många för att patentera, så istället släpptes informationen till allmän egendom för att förhindra någon av AT&T:s konkurrenter från att patentera dem i framtiden.
Nätverk med 2 terminaler, 2 element
En enkel impedans har två terminaler för att ansluta till omvärlden, och kan därför beskrivas som ett 2-terminals, eller ett enports , nätverk. Trots den enkla beskrivningen finns det ingen gräns för antalet maskor, och därmed komplexiteten och antalet element, som impedansnätverket kan ha. Nätverk av 2-elementtyp är vanliga i kretsdesign; filter, till exempel, är ofta LC och kretsdesigners föredrar nätverk av typen RC eftersom induktorer är mindre lätta att tillverka. Transformationer är enklare och lättare att hitta än för nätverk av tre element. Ett-element-typ-nätverk kan ses som ett specialfall av två-element-typ. är möjligt att använda transformationerna i detta avsnitt på ett fåtal nät av 3-elementstyp genom att ersätta element Zn med ett nätverk av element . Detta är dock begränsat till att maximalt två impedanser kan ersättas; resten kommer inte att vara ett fritt val. Alla transformationsekvationer som ges i detta avsnitt beror på Otto Zobel .
3-elements nätverk
Ett-elements nät är triviala och två-element, två-terminala nät är antingen två element i serie eller två element parallellt, också triviala. Det minsta antalet element som är icke-triviala är tre, och det finns två icke-triviala transformationer av 2-elementstyp möjliga, varvid den ena är både den omvända transformationen och den topologiska dualen av den andra.
4-elements nätverk
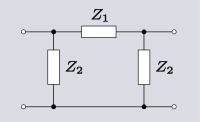
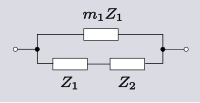
Det finns fyra icke-triviala 4-elements transformationer för 2-element-typ nätverk. Två av dessa är de omvända transformationerna av de andra två och två är dualen av två olika. Ytterligare transformationer är möjliga i det speciella fallet att Z2 görs av samma elementtyp som Z1 , det vill säga när nätverket reduceras till ett-elementtyp . Antalet möjliga nätverk fortsätter att växa i takt med att antalet element ökar. För alla poster i följande tabell är det definierat:
|
|
2-terminala, n -element, 3-element-typ nätverk

Enkla nätverk med bara ett fåtal element kan hanteras genom att formulera nätverksekvationerna "för hand" med tillämpning av enkla nätverkssatser som Kirchhoffs lagar . Ekvivalens bevisas mellan två nätverk genom att direkt jämföra de två uppsättningarna av ekvationer och likställa koefficienter . För stora nätverk krävs kraftfullare tekniker. Ett vanligt tillvägagångssätt är att börja med att uttrycka nätverket av impedanser som en matris . Detta tillvägagångssätt är bara bra för rationella nätverk. Alla nätverk som innehåller distribuerade element , såsom en transmissionsledning , kan inte representeras av en ändlig matris. I allmänhet kräver ett n -mesh-nätverk en n x n matris för att representera det. Till exempel kan matrisen för ett 3-mesh-nätverk se ut
Matrisens poster väljs så att matrisen bildar ett system av linjära ekvationer i nätspänningarna och strömmarna (enligt definitionen för nätanalys ):
Exempeldiagrammet i figur 1 kan till exempel representeras som en impedansmatris av
och det associerade systemet med linjära ekvationer är
I det mest allmänna fallet kan varje gren Zp av nätet vara uppbyggd av tre element så att
där L , R och C representerar induktans , resistans och kapacitans respektive och s är den komplexa frekvensoperatorn s .
allmän impedans, men för denna artikels syften är det matematiskt bekvämare att hantera elastans , D , inversen av kapacitans, C. I dessa termer kan den allmänna grenimpedansen representeras av
På samma sätt kan varje ingång i impedansmatrisen bestå av summan av tre element. Följaktligen kan matrisen delas upp i tre n x n matriser, en för var och en av de tre elementtyperna:
Det är önskvärt att matrisen [ Z ] representerar en impedans, Z ( s ). För detta ändamål skärs öglan av en av maskorna och Z ( s ) är impedansen som mäts mellan punkterna så skurna. Det är konventionellt att anta att den externa anslutningsporten är i mesh 1 och därför är ansluten över matrisingången Z11 , även om det skulle vara fullt möjligt att formulera detta med anslutningar till alla önskade noder. I den följande diskussionen antas Z ( s ) tagna över Z11 . Z ( s ) kan beräknas från [ Z ] av
där z 11 är komplementet till Z 11 och | Z | är determinanten för [ Z ].
För exempelnätverket ovan,
- och
Detta resultat är lätt verifierat att vara korrekt med den mer direkta metoden med motstånd i serie och parallella. Sådana metoder blir dock snabbt tråkiga och besvärliga med tillväxten av storleken och komplexiteten hos nätverket som analyseras.
Inmatningarna för [ R ], [ L ] och [ D ] kan inte ställas in godtyckligt. För att [ Z ] ska kunna realisera impedansen Z ( s ) måste [ R ],[ L ] och [ D ] alla vara positiv-definita matriser . Även då kommer realiseringen av Z ( s ) i allmänhet att innehålla idealiska transformatorer inom nätverket. Att bara hitta de transformer som inte kräver ömsesidiga induktanser eller idealiska transformatorer är en svårare uppgift. På liknande sätt, om man börjar från den "andra änden" och anger ett uttryck för Z ( s ), kan detta återigen inte göras godtyckligt. För att kunna realiseras som en rationell impedans Z ( s ) vara positiv-reell . Det positiva-verkliga (PR)-villkoret är både nödvändigt och tillräckligt, men det kan finnas praktiska skäl för att förkasta vissa topologier .
En generell impedanstransform för att hitta ekvivalenta rationella enportar från en given instans av [ Z ] beror på Wilhelm Cauer . Gruppen av verkliga affina transformationer
- där
är invariant i Z ( s ). Det vill säga att alla transformerade nätverk är ekvivalenter enligt definitionen som ges här. Om Z ( s ) för den initiala givna matrisen är realiserbar, det vill säga den uppfyller PR-villkoret, kommer alla de transformerade nätverk som produceras av denna transformation också att uppfylla PR-villkoret.
3- och 4-terminalsnätverk

När man diskuterar nätverk med 4 terminaler, fortsätter nätverksanalys ofta i termer av 2-portsnätverk, som täcker ett stort antal praktiskt användbara kretsar. "2-portar" syftar i huvudsak på hur nätverket har kopplats till omvärlden: att terminalerna har kopplats parvis till en källa eller last. Det är möjligt att ta exakt samma nätverk och ansluta det till externa kretsar på ett sådant sätt att det inte längre beter sig som en 2-port. Denna idé visas i figur 2.
Ett nätverk med 3 terminaler kan också användas som 2-portar. För att uppnå detta ansluts en av terminalerna gemensamt till en terminal på båda portarna. Med andra ord har en terminal delats upp i två terminaler och nätet har i praktiken konverterats till ett 4-terminals nät. Denna topologi är känd som obalanserad topologi och står i motsats till balanserad topologi. Balanserad topologi kräver, med hänvisning till figur 3, att impedansen uppmätt mellan terminalerna 1 och 3 är lika med impedansen som uppmätts mellan 2 och 4. Detta är paren av terminaler som inte bildar portar: fallet då paren av terminaler som bildar portar har lika stora impedans kallas symmetrisk . Strängt taget är alla nätverk som inte uppfyller balansvillkoret obalanserat, men termen syftar oftast på 3-terminalstopologin som beskrivs ovan och i figur 3. Att omvandla ett obalanserat 2-portsnätverk till ett balanserat nätverk är vanligtvis ganska enkelt : alla seriekopplade element är uppdelade på mitten och ena hälften flyttas till det som var den gemensamma grenen. Att transformera från balanserad till obalanserad topologi kommer ofta att vara möjligt med omvänd transformation, men det finns vissa fall av vissa topologier som inte kan transformeras på detta sätt. Se till exempel diskussionen om gittertransformer nedan.
Ett exempel på en 3-terminals nätverkstransform som inte är begränsad till 2-portar är Y-Δ-transformen . Detta är en särskilt viktig transformation för att hitta ekvivalenta impedanser. Dess betydelse härrör från det faktum att den totala impedansen mellan två terminaler inte kan bestämmas enbart genom att beräkna serie- och parallellkombinationer förutom för en viss begränsad klass av nätverk. I det allmänna fallet krävs ytterligare omvandlingar. Y-A-transformen, dess inversa Δ-Y-transformen och de n -terminala analogerna av dessa två transformer ( stjärna-polygon-transformationer) representerar de minimala ytterligare transformationer som krävs för att lösa det allmänna fallet. Serier och parallella är i själva verket de 2-terminala versionerna av stjärn- och polygontopologi. En vanlig enkel topologi som inte kan lösas med serie- och parallellkombinationer är ingångsimpedansen till ett bryggnät (förutom i det speciella fallet då bryggan är i balans). Resten av transformationerna i det här avsnittet är alla begränsade till användning med endast 2-portar.
Gitter transformeras
Symmetriska 2-portsnätverk kan omvandlas till gitternätverk med hjälp av Bartletts bisektionssats . Metoden är begränsad till symmetriska nätverk men detta inkluderar många topologier som vanligtvis finns i filter, dämpare och utjämnare . Gittertopologin är i sig balanserad, det finns ingen obalanserad motsvarighet till gittret och det kommer vanligtvis att kräva fler komponenter än det transformerade nätverket.
Omvända transformationer från ett gitter till en obalanserad topologi är inte alltid möjliga när det gäller passiva komponenter. Till exempel denna transformation:
| Beskrivning | Nätverk | Förvandlat nätverk |
|---|---|---|
|
Transform 3.4 Transformering av en gitterfasutjämnare till ett T-nätverk. |

|

|
kan inte realiseras med passiva komponenter på grund av de negativa värden som uppstår i den transformerade kretsen. Det kan dock realiseras om ömsesidiga induktanser och idealiska transformatorer är tillåtna, till exempel i denna krets . En annan möjlighet är att tillåta användning av aktiva komponenter som skulle möjliggöra att negativa impedanser direkt realiseras som kretskomponenter.
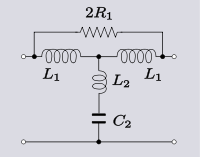
Det kan ibland vara användbart att göra en sådan transformation, inte i syfte att faktiskt bygga den transformerade kretsen, utan snarare i syfte att hjälpa förståelsen av hur den ursprungliga kretsen fungerar. Följande krets i bryggad-T-topologi är en modifiering av en mellanseriens m-härledd filter- T-sektion. Kretsen beror på Hendrik Bode som hävdar att tillägget av bryggmotståndet med ett lämpligt värde kommer att upphäva parasitmotståndet hos shuntinduktorn. Denna krets verkan är tydlig om den omvandlas till T-topologi - i denna form finns det ett negativt motstånd i shuntgrenen som kan göras exakt lika med induktorns positiva parasitresistans.
| Beskrivning | Nätverk | Förvandlat nätverk |
|---|---|---|
|
Transform 3.5 Transform av en bryggad T- lågpassfiltersektion till en T-sektion. |
|

|
Vilket symmetriskt nätverk som helst kan omvandlas till vilket annat symmetriskt nätverk som helst med samma metod, det vill säga genom att först transformera till den mellanliggande gitterformen (utelämnad för tydlighetens skull från ovanstående exempeltransformation) och från gitterformen till den önskade målformen. Precis som i exemplet kommer detta i allmänhet att resultera i negativa element utom i speciella fall.
Eliminera motstånd
Ett teorem som beror på Sidney Darlington säger att vilken PR-funktion Z ( s ) som helst kan realiseras som en förlustfri tvåportar som avslutas i ett positivt motstånd R. Det vill säga oavsett hur många motstånd som finns i matrisen [ Z ] som representerar impedansnätverket , kan en transform hittas som kommer att realisera nätverket helt som ett nätverk av LC-typ med bara ett motstånd över utgångsporten (som normalt skulle representera belastningen). Inga motstånd inom nätverket behövs för att realisera det specificerade svaret. Följaktligen är det alltid möjligt att reducera 3-element-typ 2-portsnätverk till 2-element-typ (LC) 2-portsnätverk förutsatt att utgångsporten avslutas i en resistans av det önskade värdet.
Eliminerar idealiska transformatorer
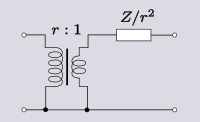
En elementär transformation som kan göras med idealiska transformatorer och något annat impedanselement är att flytta impedansen till den andra sidan av transformatorn. I alla följande transformeringar r transformatorns varvförhållande.
Dessa omvandlingar gäller inte bara enskilda element; hela nätverk kan passeras genom transformatorn. På detta sätt kan transformatorn flyttas runt nätverket till en mer bekväm plats.
Darlington ger en likvärdig transformator som kan eliminera en ideal transformator helt och hållet. Denna teknik kräver att transformatorn är bredvid (eller kan flyttas bredvid) ett "L"-nätverk av samma typ av impedanser. Transformen i alla varianter resulterar i att "L"-nätverket är vänt åt motsatt håll, det vill säga topologiskt speglat.
| Beskrivning | Nätverk | Förvandlat nätverk |
|---|---|---|
|
Transform 5.1 Eliminering av en nedtrappningstransformator. |

|

|
|
Transform 5.2 Eliminering av en step-up transformator. |

|

|
|
Exempel 3. Exempel på transformation 5.1. |

|

|
Exempel 3 visar att resultatet är ett Π-nätverk snarare än ett L-nätverk. Anledningen till detta är att shuntelementet har mer kapacitans än vad som krävs av transformationen så en del är fortfarande över efter applicering av transformationen. Om överskottet istället fanns i elementet närmast transformatorn, skulle detta kunna hanteras genom att först flytta överskottet till andra sidan av transformatorn innan omvandlingen genomfördes.
Terminologi
Bibliografi
- Bartlett, AC , "En förlängning av en egenskap hos artificiella linjer", Phil. Mag. , vol 4 , s. 902, november 1927.
- Belevitch, V. , "Sammanfattning av kretsteoriens historia", Proceedings of the IRE , vol 50 , Iss 5, s.848-855, maj 1962.
- E. Cauer, W. Mathis och R. Pauli, "Life and Work of Wilhelm Cauer (1900 – 1945)", Proceedings of the Fourteenth International Symposium of Mathematical Theory of Networks and Systems , Perpignan, juni 2000.
- Foster, Ronald M. ; Campbell, George A. , "Maximum output networks for phone substation and repeater circuits" , Transactions of the American Institute of Electrical Engineers , vol.39 , iss.1, s.230-290, januari 1920.
- Darlington, S. , "En historia av nätverkssyntes och filterteori för kretsar som består av resistorer, induktorer och kondensatorer", IEEE Trans. Circuits and Systems , vol 31 , s. 3-13, 1984.
- Farago, PS, An Introduction to Linear Network Analysis , The English Universities Press Ltd, 1961.
- Khan, Sameen Ahmed, "Farey-sekvenser och motståndsnätverk" , Proceedings of the Indian Academy of Sciences (Mathematical Sciences) , vol.122 , iss.2, s. 153-162, maj 2012.
- Zobel, OJ , Teori och design av enhetliga och sammansatta elektriska vågfilter, Bell System Technical Journal, Vol. 2 (1923), sid. 1-46.



















































![{\mathbf {[Z]}}={\begin{bmatrix}Z_{{11}}&Z_{{12}}&Z_{{13}}\\Z_{{21}}&Z_{{22}}&Z_{{23}}\\Z_{{31}}&Z_{{32}}&Z_{{33}}\end{bmatrix}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a3ad5a75d23711b0a6b9076315e08048ecc6ad5)
![{\mathbf {[V]}}={\mathbf {[Z][I]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7641bc53ed8dad8a6ced24e7e09a788235db0736)
![{\mathbf {[Z]}}={\begin{bmatrix}R_{1}+R_{2}&-R_{2}\\-R_{2}&R_{2}+R_{3}\end{bmatrix}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3307f9ced33526217885f1024e854e23610efc0)




![s{\mathbf {[Z]}}=s^{2}{\mathbf {[L]}}+s{\mathbf {[R]}}+{\mathbf {[D]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f37cbea3f2334c58706db3ad40139f76d8d1f375)




![{\mathbf {[Z']}}={\mathbf {[T]}}^{T}{\mathbf {[Z]}}{\mathbf {[T]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e7b431d0275bca3e9a12be141b0630c789867b2)
![{\mathbf {[T]}}={\begin{bmatrix}1&0\cdots 0\\T_{{21}}&T_{{22}}\cdots T_{{2n}}\\\cdot &\cdots \\T_{{n1}}&T_{{n2}}\cdots T_{{nn}}\end{bmatrix}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5843c3ee96f594963075b4131cc46dbf79ad3593)