Drakkungens teori
Dragon king (DK) är en dubbel metafor för en händelse som är både extremt stor i storlek eller inverkan (en "kung") och född av unikt ursprung (en "drake") i förhållande till sina jämnåriga (andra händelser från samma system) . DK-händelser genereras av eller motsvarar mekanismer som positiv feedback , tipppunkter , bifurkationer och fasövergångar , som tenderar att inträffa i olinjära och komplexa system , och tjänar till att förstärka DK-händelser till extrema nivåer. Genom att förstå och övervaka denna dynamik kan en viss förutsägbarhet av sådana händelser erhållas.
Drakungsteorin utvecklades av Didier Sornette , som antar att många kriser i själva verket är DK:er snarare än svarta svanar - dvs de kan vara förutsägbara till viss del. Med tanke på krisernas betydelse för den långsiktiga organisationen av en mängd olika system, uppmanar DK-teorin att särskild uppmärksamhet ägnas åt studier och övervakning av extremer, och att en dynamisk syn tas. Ur vetenskaplig synvinkel är sådana ytterligheter intressanta eftersom de kan avslöja underliggande, ofta dolda, organiserande principer. Rent praktiskt bör man studera extrema risker, men inte glömma att betydande osäkerhet nästan alltid kommer att finnas, och bör noggrant beaktas i beslut om riskhantering och design.
DK-teorin är relaterad till begrepp som black swan-teori, extremvärden , komplexa system , olinjär dynamik , maktlagar , extremvärdesteori , förutsägelse , extrema risker och riskhantering .
Svarta svanar och drakungar
En svart svan kan betraktas som en metafor för en händelse som är överraskande (för betraktaren), har en stor effekt och, efter att ha observerats, rationaliseras i efterhand. Teorin om svarta svanar är epistemologisk och relaterar till observatörens begränsade kunskap och förståelse. Termen introducerades och populariserades av Nassim Taleb och har förknippats med begrepp som tunga svansar , icke-linjära vinster, modellfel och till och med riddarisk osäkerhet , vars "okänd okänd" händelseterminologi populariserades av USA:s förre försvarsminister Donald Rumsfeld. Taleb hävdar att svarta svanhändelser inte är förutsägbara, och i praktiken uppmuntrar teorin en att "förbereda sig snarare än att förutsäga", och begränsa sin exponering för extrema fluktuationer.
Begreppet svart svan är viktigt och utgör en giltig kritik av människor, företag och samhällen som är oansvariga i den meningen att de är alltför säkra på sin förmåga att förutse och hantera risker. Men att hävda att extrema händelser är – i allmänhet – oförutsägbara kan också leda till bristande ansvarighet i riskhanteringsroller. Faktum är att det är känt att extrema händelser i ett brett spektrum av fysiska system är förutsägbara i viss mån. Man behöver helt enkelt ha en tillräckligt djup förståelse för fokalsystemets struktur och dynamik, och förmågan att övervaka det. Detta är drakungarnas domän. Sådana händelser har kallats "grå svanar" av Taleb. En mer rigorös åtskillnad mellan svarta svanar, grå svanar och drakungar är svår eftersom svarta svanar inte är exakt definierade i fysiska och matematiska termer. Teknisk utarbetning av begrepp i Black Swan -boken utvecklas dock i Silent Risk-dokumentet. En analys av den exakta definitionen av en svart svan i riskhanteringssammanhang skrevs av professor Terje Aven.
Bortom maktlagar

Det är välkänt att många fenomen inom både natur- och samhällsvetenskapen har maktlagsstatistik ( Paretodistribution ) . Dessutom, från extremvärdesteorin, är det känt att ett brett spektrum av distributioner (Frechet-klassen) har svansar som är asymptotiskt maktlag. Resultatet av detta är att, när man hanterar kriser och extremer, är maktlagssvansar det "normala" fallet. Den unika egenskapen hos maktlagar är att de är skalinvarianta , självlika och fraktala . Den här egenskapen antyder att alla händelser – både stora och små – genereras av samma mekanism, och därför kommer det inte att finnas några distinkta prekursorer genom vilka de största händelserna kan förutsägas. Ett välkänt konceptuellt ramverk för händelser av denna typ är självorganiserad kritikalitet . Sådana begrepp är förenliga med teorin om den svarta svanen. Men Taleb har också sagt att om man betraktar maktlagen som en modell istället för en modell med ljusare svansar (t.ex. en gaussisk ) "konverterar svarta svanar till gråa", i den meningen att maktlagsmodellen ger en icke försumbar sannolikhet till stor evenemang.
I en mängd olika studier har det visat sig att, trots att en maktlag modellerar svansen av den empiriska fördelningen väl, är de största händelserna väsentligt utanför (dvs. mycket större än vad som skulle förväntas under modellen). Sådana händelser tolkas som drakungar eftersom de indikerar ett avsteg från den generiska processen som ligger till grund för maktlagen. Exempel på detta inkluderar de största utsläppshändelserna av strålning som inträffar vid kärnkraftsolyckor, den största staden (agglomerationen) inom urvalet av städer i ett land, de största kraschen på finansmarknaderna och elpriser i grossistledet under dagen.
Mekanismer
Fysiskt sett kan drakungar vara förknippade med regimförändringar, bifurkationer och vändpunkter för komplexa system som inte är i jämvikt. Till exempel katastrofen ( veckbifurkationen ) för den globala ekologin som illustreras i figuren anses vara en drakung: Många observatörer skulle bli överraskade av en sådan dramatisk förändring av tillståndet. Det är dock välkänt att i dynamiska system finns det många prekursorer när systemet närmar sig katastrofen.
Positiv feedback är också en mekanism som kan skapa drakungar. Till exempel, i en rasering ökar antalet nötkreatur som springer nivån av panik som får fler nötkreatur att springa, och så vidare. Inom mänsklig dynamik har sådant vallnings- och pöbelbeteende också observerats i folkmassor, aktiemarknader och så vidare (se flockbeteende ).
Drakungar orsakas också av attraktionsbubblande i kopplade oscillatorsystem . Attraktionsbubbling är ett generiskt beteende som uppträder i nätverk av kopplade oscillatorer där systemet vanligtvis kretsar i ett oföränderligt grenrör med en kaotisk attraktion (där toppbanorna är låga), men intermittent skjuts in (av brus) in i en region där banor avstöts lokalt från det invarianta grenröret (där toppbanorna är stora). Dessa utflykter bildar drakungarna, som illustreras i figuren. Det hävdas att sådana modeller kan beskriva många verkliga fenomen som jordbävningar, hjärnaktivitet etc. En block- och fjädermekanisk modell, betraktad som en modell av geologiska förkastningar och deras jordbävningsdynamik, gav en liknande fördelning.
Det kan också vara så att drakungar skapas som ett resultat av systemkontroll eller intervention. Det vill säga att försöka undertrycka frigörandet av stress eller död i dynamiska komplexa system kan leda till en ansamling av stress eller en mognad mot instabilitet. Till exempel borst- / skogsbränder en naturlig företeelse i många områden. Sådana bränder är obekväma och därför kan vi önska att de flitigt släcks. Detta leder till långa perioder utan obekväma bränder, men i frånvaro av bränder ansamlas död ved. När väl denna ansamling når en kritisk punkt, och en brand startar, blir elden så stor att den inte kan kontrolleras – en unik händelse som kan anses vara en drakung. Andra policyer, som att inte göra någonting (tillåta att små bränder uppstår naturligt) eller att utföra strategisk kontrollerad förbränning , skulle undvika enorma bränder genom att tillåta frekventa små bränder. Ett annat exempel är penningpolitiken . Program för kvantitativa lättnader och lågräntepolitik är vanliga, med avsikten att undvika lågkonjunkturer, främja tillväxt etc. Sådana program skapar dock instabilitet genom att öka inkomstskillnaderna, hålla svaga företag vid liv och blåsa upp tillgångsbubblor. I slutändan kommer en sådan politik, som syftar till att jämna ut ekonomiska fluktuationer, möjliggöra en enorm korrigering – en drakung.
Upptäcker DK som statistiska extremvärden
DK:er är avvikande per definition. Men när man kallar DKs för extremvärden finns det ett viktigt förbehåll: I standardstatistik är extremvärden vanligtvis felaktiga värden och kasseras, eller så väljs statistiska metoder som på något sätt är okänsliga för extremvärden. Tvärtemot är DK:er extremvärden som är mycket informativa och bör vara i fokus för mycket statistisk uppmärksamhet. Ett första steg är således att identifiera DK:er i historiska data. Befintliga tester är antingen baserade på de asymptotiska egenskaperna hos den empiriska fördelningsfunktionen (EDF) eller på ett antagande om den underliggande kumulativa fördelningsfunktionen (CDF) för data.
Det visar sig att testning av extremvärden i förhållande till en exponentiell fördelning är mycket generell. Det senare följer av Pickands–Balkema–de Haans sats om extremvärdesteorin som säger att ett brett spektrum av distributioner asymptotiskt (över höga trösklar) har exponentiella eller kraftlagssvansar. För övrigt är detta en förklaring till varför maktlagssvansar är så vanliga när man studerar extremer. För att avsluta poängen, eftersom den naturliga logaritmen för en kraftlagssvans är exponentiell, kan man ta logaritmen för kraftlagsdata och sedan testa för extremvärden i förhållande till en exponentiell svans. Det finns många teststatistik och tekniker för att testa för extremvärden i ett exponentiellt urval. Ett inåtgående test testar sekventiellt den största punkten, sedan den näst största, och så vidare, tills det första testet som inte förkastas (dvs. nollhypotesen att punkten inte är en extremvärde förkastas inte). Antalet avvisade tester identifierar antalet extremvärden. Till exempel, där sorterade provet, det inåtriktade robusta testet använder teststatistiken där r är den punkt som testas och där m är det fördefinierade maximala antalet extremvärden. Vid varje steg p-värdet för teststatistiken beräknas och, om det är lägre än någon nivå, testet avvisas. Det här testet har många önskvärda egenskaper: Det kräver inte att antalet extremvärden specificeras, det är inte benäget att under- (maskera) och över (svampa) uppskattning av antalet extremvärden, det är lätt att implementera och testet är oberoende av värdet på parametern för den exponentiella svansen.
Exempel

Några exempel på var drakungar har upptäckts som extremvärden inkluderar:
- finansiella krascher mätt med uttag , där extremvärdena motsvarar terroristattacker (t.ex. bombattentatet i London 2005 ) och snabbkraschen 2010 ;
- strålning som frigörs och ekonomiska förluster orsakade av olyckor vid kärnkraftverk, där extremvärden motsvarar skenkatastrofer där säkerhetsmekanismerna var överväldigade;
- den största staden (mätt med befolkningen i dess tätort) i befolkningen i städer inom ett land, där den största staden spelar en oproportionerligt viktig roll i landets dynamik och drar nytta av unik tillväxt;
- elpriser i grossistledet inom dagen; och
- ickelinjär interaktion med tre vågor – det är möjligt att undertrycka uppkomsten av drakungar.
Modellering och förutsägelse
Hur man modellerar och förutsäger drakungar beror på den underliggande mekanismen. Det gemensamma tillvägagångssättet kommer dock att kräva kontinuerlig övervakning av fokalsystemet och jämförelse av mätningar med en ( icke-linjär eller komplex ) dynamisk modell. Det har föreslagits att ju mer homogent systemet är, och ju starkare dess interaktioner, desto mer förutsägbart kommer det att vara.
Till exempel, i icke-linjära system med fasövergångar vid en kritisk punkt, är det välkänt att ett fönster av förutsägbarhet uppstår i närheten av den kritiska punkten på grund av prekursoriska tecken: systemet återhämtar sig långsammare från störningar, autokorrelationsförändringar, varians ökningar, spatial koherens ökar, etc. Dessa egenskaper har använts för förutsägelse i många tillämpningar, allt från förändringar i biosfären till bristning av trycktankar på Ariane-raketen. Tillämpningarna på ett brett spektrum av fenomen har stimulerat det komplexa systemperspektivet, som är ett tvärvetenskapligt tillvägagångssätt och inte är beroende av den första principens förståelse.
För fenomenen ohållbar tillväxt (t.ex. befolkningar eller aktiekurser) kan man överväga en tillväxtmodell som har en ändlig tidssingularitet, vilket är en kritisk punkt där tillväxtregimen förändras. I system som är diskreta skalinvarianter är en sådan modell effektlagstillväxt, dekorerad med en log-periodisk funktion. Att anpassa denna modell på tillväxtdata ( icke-linjär regression ) möjliggör förutsägelse av singulariteten, dvs slutet på ohållbar tillväxt. Detta har tillämpats på många problem, till exempel: brott i material, jordbävningar och tillväxten och sprängningen av bubblor på finansmarknaderna
En intressant dynamik att överväga, som kan avslöja utvecklingen av en storframgång, är epidemiska fenomen : t.ex. spridningen av pest, virusfenomen i media, spridningen av panik och volatilitet på aktiemarknaderna, etc. I ett sådant fall , ett kraftfullt tillvägagångssätt är att bryta ned aktivitet/fluktuationer i exogena och endogena delar, och lära sig om den endogena dynamiken som kan leda till kraftiga utbrott i aktivitet.
Förutsägelse och beslutsfattande
Givet en modell och data kan man få en statistisk modelluppskattning. Denna modelluppskattning kan sedan användas för att beräkna intressanta storheter såsom den villkorade sannolikheten för att en drakungshändelse ska inträffa i ett framtida tidsintervall och den mest sannolika förekomsttiden. När man gör statistisk modellering av extremer och använder komplexa eller icke-linjära dynamiska modeller, är det oundvikligen stor osäkerhet. Således bör man vara noggrann med osäkerhetskvantifiering: inte bara med tanke på slumpmässigheten som finns i den anpassade stokastiska modellen, utan också osäkerheten hos dess uppskattade parametrar (t.ex. med Bayesianska tekniker eller genom att först simulera parametrar och sedan simulera från modellen med dessa parametrar ), och osäkerheten i modellvalet (t.ex. genom att överväga en ensemble av olika modeller).
Man kan sedan använda de uppskattade sannolikheterna och deras tillhörande osäkerheter för att informera beslut. I det enklaste fallet utför man en binär klassificering : att förutsäga att en drakung kommer att inträffa i ett framtida intervall om dess sannolikhet är tillräckligt hög, med tillräcklig säkerhet. Till exempel kan man vidta en specifik åtgärd om en drakung förutspås inträffa. Ett optimalt beslut kommer då att balansera kostnaden för falska negativa / falska positiva och missade / falska larm enligt en specificerad förlustfunktion . Till exempel, om kostnaden för en miss är mycket stor i förhållande till kostnaden för ett falskt larm, kommer det optimala beslutet att upptäcka drakungar oftare än de inträffar. Man bör också studera den sanna positiva frekvensen av förutsägelsen. Ju lägre detta värde är, desto svagare är testet, och desto närmare den svarta svanens territorium. I praktiken måste valet av det optimala beslutet och beräkningen av dess egenskaper göras genom korsvalidering med historiska data (om tillgängliga), eller på simulerade data (om man vet hur man simulerar drakungarna).
I en dynamisk miljö kommer datasetet att växa över tiden, och modelluppskattningen och dess uppskattade sannolikheter kommer att utvecklas. Man kan då överväga att kombinera sekvensen av uppskattningar/sannolikheter när man gör förutsägelser. I denna dynamiska miljö kommer testet sannolikt att vara svagt för det mesta (t.ex. när systemet är runt jämvikt), men när man närmar sig en drakkung och prekursorer blir synliga bör den sanna positiva frekvensen öka.
Vikten av extrema risker
Drakungar bildar speciella typer av händelser som leder till extrema risker (vilket också kan vara möjligheter). Att extrema risker är viktiga och borde vara självklart. Naturkatastrofer ger många exempel (t.ex. asteroidnedslag som leder till utrotning). Några statistiska exempel på effekterna av extremer är att: den största kärnkraftsolyckan ( Tjernobyl-katastrofen ) hade en ungefär lika stor skadekostnad (mätt som beräknad kostnad i US-dollar) som alla (+- 175) andra historiska kärnkraftsolyckor tillsammans, de största 10 procenten av privata dataintrång från organisationer står för 99 procent av den totala intrångade privata informationen, de största fem epidemierna sedan 1900 orsakade 20 gånger fler dödsfall än de återstående 1363, etc. I allmänhet kommer sådan statistik i närvaro av tunga svansar. distributioner och närvaron av drakungar kommer att förstärka den redan överdimensionerade effekten av extrema händelser.
Trots vikten av extrema händelser, på grund av okunnighet, felaktiga incitament och kognitiva fördomar, är det ofta ett misslyckande att förutse dem på ett adekvat sätt. Tekniskt sett leder detta till dåligt specificerade modeller där distributioner som inte är tillräckligt kraftiga svansar och underskattar både seriellt och multivariat beroende av extrema händelser. Några exempel på sådana misslyckanden i riskbedömning inkluderar användningen av Gaussiska modeller inom finans ( Black–Scholes , Gaussisk kopula, LTCM ), användningen av Gaussiska processer och linjär vågteori som misslyckas med att förutsäga förekomsten av oseriösa vågor , misslyckande av ekonomiska modeller i allmänhet för att förutsäga finanskrisen 2007–2008 och underskattningen av externa händelser, kaskader och icke-linjära effekter i probabilistisk riskbedömning , vilket leder till att man inte förutser kärnkraftskatastrofen i Fukushima Daiichi 2011. Sådana misslyckanden med stor påverkan betonar vikten av att studera extremer.
Riskhantering
Drakkungens koncept väcker många frågor om hur man kan hantera risker. Naturligtvis, om möjligt, bör exponering för stora risker undvikas (ofta kallad "svarta svanens ansats"). Men i många utvecklingar är exponering för risk en nödvändighet, och en avvägning mellan risk och avkastning måste navigeras.
I ett adaptivt system, där förutsägelse av drakungar är framgångsrik, kan man agera för att försvara systemet eller till och med tjäna pengar. Hur man designar sådana motståndskraftiga system , såväl som deras riskövervakningssystem i realtid, är ett viktigt och tvärvetenskapligt problem där drakungar måste beaktas.
Å andra sidan, när det gäller kvantifiering av risk i ett givet system (oavsett om det är en bank, ett försäkringsbolag, en vall, en bro eller ett socioekonomiskt system), måste risken redovisas över en period , såsom årligen. Vanligtvis är man intresserad av statistik som den årliga sannolikheten för förlust eller skada som överstiger något värde ( value at risk ), andra svansriskmått och returperioder . För att ge sådana riskkarakteriseringar måste de dynamiska drakungarna resoneras om i termer av årlig frekvens- och svårighetsstatistik. Denna statistik över frekvens och svårighetsgrad kan sedan sammanföras i en modell som en sammansatt Poisson-process .
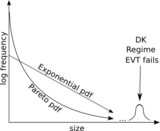
Förutsatt att de statistiska egenskaperna hos systemet är konsekventa över tiden (stationära), kan frekvens- och svårighetsstatistik konstrueras baserat på tidigare observationer, simuleringar och/eller antaganden. Om inte kan man bara konstruera scenarier. Med tanke på den osäkerhet som råder bör dock en rad scenarier övervägas. På grund av bristen på data för extrema händelser, principen om sparsamhet och teoretiska resultat från extremvärdesteori om universella svansmodeller, förlitar man sig vanligtvis på en generaliserad Pareto-distribution (GPD) svansmodell. En sådan modell utesluter dock DK. Således, när man har tillräckliga skäl att tro att DK:er finns, eller om man helt enkelt vill överväga ett scenario, kan man t.ex. överväga en densitetsblandning av en GPD och en densitet för DK-regimen.