Hypohamiltonian graf

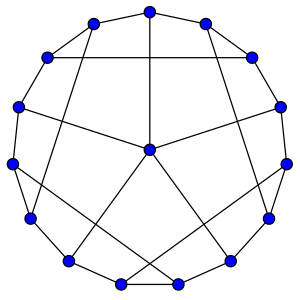
Ej att förväxla med Hamiltonsk graf .
En hypohamiltonsk graf konstruerad av Lindgren (1967) .

Inom det matematiska fältet för grafteorin sägs en graf G vara hypohamiltonisk om G själv inte har en Hamiltonsk cykel utan varje graf som bildas genom att ta bort en enda vertex från G är Hamiltonsk .

Historia

Hypohamiltoniska grafer studerades först av Sousselier (1963) . Lindgren (1967) citerar Gaudin, Herz & Rossi (1964) och Busacker & Saaty (1965) som ytterligare tidiga artiklar i ämnet; ett annat tidigt verk är av Herz, Duby & Vigué (1967) .

Grötschel (1980) sammanfattar mycket av forskningen inom detta område med följande mening: "Artiklarna som handlar om dessa grafer ... uppvisar vanligtvis nya klasser av hypohamiltoniska eller hypospårbara grafer som visar att det för vissa ordningar verkligen finns sådana grafer eller att de besitter konstiga och oväntade egenskaper."

Ansökningar

Hypohamiltonska grafer uppstår i heltalsprogrammeringslösningar för resandeförsäljarproblemet : vissa typer av hypohamiltonska grafer definierar aspekter av den resande försäljarpolytopen , en form som definieras som det konvexa skrovet av uppsättningen av möjliga lösningar på resandeförsäljarproblemet, och dessa aspekter kan vara används i skärplansmetoder för att lösa problemet. Grötschel (1980) observerar att beräkningskomplexiteten för att avgöra om en graf är hypohamiltonsk, även om den är okänd, sannolikt är hög, vilket gör det svårt att hitta aspekter av dessa typer förutom de som definieras av små hypohamiltonska grafer; lyckligtvis leder de minsta graferna till de största ojämlikheterna för denna applikation.

Begrepp som är nära relaterade till hypohamiltonicitet har också använts av Park, Lim & Kim (2007) för att mäta feltoleransen för nätverkstopologier för parallell beräkning .

Egenskaper

Varje hypohamiltonsk graf måste vara 3- vertex-connected , eftersom borttagandet av två hörn lämnar en Hamiltonsk bana, som är ansluten. Det finns n -vertex hypohamiltoniska grafer där den maximala graden är n /2 och där det finns ungefär n 2 /4 kanter.

Thomassens (1974b) omkrets-3 hypohamiltonian graf.

Herz, Duby & Vigué (1967) antog att varje hypohamiltonsk graf har omkrets 5 eller mer, men detta motbevisades av Thomassen (1974b), som hittade exempel med omkrets 3 och 4. Under en tid var det okänt om en hypohamiltonsk graf kunde vara planar , men flera exempel är nu kända, varav det minsta har 40 hörn. Varje plan hypohamiltonisk graf har minst en vertex med endast tre infallande kanter.

Om en 3-regelbunden graf är Hamiltonsk, kan dess kanter färgas med tre färger: använd alternerande färger för kanterna på Hamiltonska cykeln (som måste ha jämn längd enligt handskakningslemma) och en tredje färg för alla återstående kanter. Därför måste alla snarks , brolösa kubiska grafer som kräver fyra kantfärger, vara icke-hamiltonska, och många kända snarks är hypohamiltonska. Varje hypohamiltonisk snark är bikritisk : att ta bort två valfria hörn lämnar en subgraf vars kanter kan färgas med endast tre färger. En trefärgning av denna subgraf kan enkelt beskrivas: efter att ha tagit bort en vertex innehåller de återstående hörnen en Hamiltonsk cykel. Efter att ha tagit bort en andra vertex blir denna cykel en bana, vars kanter kan färgas genom att växla mellan två färger. De återstående kanterna bildar en matchning och kan färgas med en tredje färg.

Färgklasserna för varje 3-färgning av kanterna på en 3-regelbunden graf bildar tre matchningar så att varje kant hör till exakt en av matchningarna. Hypohamiltoniska snarkar har ingen uppdelning i matchningar av denna typ, men Häggkvist (2007) gissar att kanterna på en hypohamiltonisk snark kan användas för att bilda sex matchningar så att varje kant tillhör exakt två av matchningarna. Detta är ett specialfall av Berge–Fulkersons gissning att varje snark har sex matchningar med den här egenskapen.

Hypohamiltonska grafer kan inte vara tvådelade: i en tvådelad graf kan en vertex bara tas bort för att bilda en Hamiltonsk subgraf om den tillhör den största av grafens två färgklasser. Emellertid förekommer varje tvådelad graf som en inducerad subgraf av någon hypohamiltonisk graf.

Exempel

Den minsta hypohamiltonska grafen är Petersen-grafen ( Herz, Duby & Vigué 1967) . Mer allmänt är den generaliserade Petersen-grafen GP( n ,2) hypohamiltonisk när n är 5 (mod 6); Petersen-grafen är instansen av denna konstruktion med n = 5.

Lindgren (1967) hittade en annan oändlig klass av hypohamiltonska grafer där antalet hörn är 4 (mod 6). Lindgrens konstruktion består av en cykel av längd 3 (mod 6) och en enda central vertex; den centrala vertexen är ansluten till var tredje hörn av cykeln med kanter som han kallar ekrar, och hörnen två positioner bort från varje ekerändpunkt är anslutna till varandra. Återigen, det minsta exemplet på Lindgrens konstruktion är Petersen-grafen.

Ytterligare oändliga familjer ges av Bondy (1972) , Doyen & van Diest (1975) och Gutt (1977) .

Uppräkning

Václav Chvátal bevisade 1973 att det för alla tillräckligt stora n finns en hypohamiltonisk graf med n hörn. Med hänsyn till efterföljande upptäckter är "tillräckligt stor" nu känt för att betyda att sådana grafer existerar för alla n ≥ 18. En fullständig lista över hypohamiltonska grafer med högst 17 hörn är känd: de är Petersen-grafen med 10 hörn, en 13-punktsgraf. -vertex-graf och en 15-vertex-graf hittad av datorsökningar av Herz (1968) , och fyra 16-vertex-grafer. Det finns minst tretton 18-vertex hypohamiltoniska grafer. Genom att tillämpa flip-flop-metoden enligt Chvátal (1973) på Petersen-grafen och blomsnärken är det möjligt att visa att antalet hypohamiltonska grafer, och mer specifikt antalet hypohamiltonska snarkar, växer som en exponentiell funktion av antalet av hörn.

Generaliseringar

Grafteoretiker har också studerat hypospårbara grafer , grafer som inte innehåller en Hamiltonsk väg men sådana att varje delmängd av n − 1 hörn kan vara sammankopplade med en väg. Analoga definitioner av hypohamiltonicitet och hypospårbarhet för riktade grafer har övervägts av flera författare.

En ekvivalent definition av hypohamiltoniska grafer är att deras längsta cykel har längden n − 1 och att skärningspunkten för alla längsta cykler är tom. Menke, Zamfirescu & Zamfirescu (1998) undersöker grafer med samma egenskap att skärningspunkten mellan längsta cykler är tom men där den längsta cykellängden är kortare än n − 1. Herz (1968) definierar cyklerbarheten för en graf som det största antalet k så att varje k hörn tillhör en cykel; de hypohamiltonska graferna är exakt de grafer som har cyklbarhet n − 1. På liknande sätt definierar Park, Lim & Kim (2007) en graf som ƒ- fault hamiltonian om borttagandet av högst ƒ hörn lämnar en Hamiltonsk subgraf. Schauerte & Zamfirescu (2006) studerar graferna med cyklbarhet n − 2.

Anteckningar

externa länkar

Hämtad från " https://sv.wikipedia.org/w/index.php?title=Hypohamiltonian_graph&oldid=1136098991 "