Cirkulär sektion

Ej att förväxla med cirkulär sektor .

tri-axiell ellipsoid med en cirkulär sektion

I geometri är ett cirkulärt snitt en cirkel på en quadric yta (som en ellipsoid eller hyperboloid ). Det är en speciell plan del av kvadraten, eftersom denna cirkel är skärningspunkten med kvadraten av planet som innehåller cirkeln.

Varje plan sektion av en sfär är en cirkulär sektion, om den innehåller minst 2 punkter. Varje rotationskvadrik innehåller cirklar som sektioner med plan som är ortogonala mot dess axel; den innehåller inga andra cirklar, om det inte är en sfär. Mer dolda är cirklar på andra kvadrater, såsom tri-axiala ellipsoider, elliptiska cylindrar, etc. Ändå är det sant att:

• Varje kvadratisk yta som innehåller ellipser innehåller också cirklar.

På motsvarande sätt innehåller alla kvadriska ytor cirklar utom paraboliska och hyperboliska cylindrar och hyperboliska paraboloider .

Om en fyrkant innehåller en cirkel, så är varje skärning av kvadriken med ett plan parallellt med denna cirkel också en cirkel, förutsatt att den innehåller minst två punkter. Förutom för sfärer är cirklarna i en kvadratisk, om någon, alla parallella med ett av två fasta plan (som är lika i fallet med en kvadratisk rotation).

Cirkulära sektioner används i kristallografi .

Använder projektiv geometri

De cirkulära sektionerna av en quadric kan beräknas från den implicita ekvationen av quadric, som det görs i följande avsnitt. De kan också karakteriseras och studeras genom att använda syntetisk projektiv geometri .

Låt C vara skärningspunkten mellan en kvadratisk yta Q och ett plan P . I det här avsnittet Q och C ytor i det tredimensionella euklidiska rummet , som utsträcks till det projektiva rummet över de komplexa talen . Under dessa hypoteser är kurvan C en cirkel om och endast om dess skärning med planet i oändligheten ingår i ombilicen (kurvan i oändligheten av ekvationen $x^{2} +y^{2}+z^{2}=0$ ).

Det första fallet som ska beaktas är när skärningen av Q med planet i oändligheten består av en eller två reella linjer, det vill säga när Q är antingen en hyperbolisk paraboloid , en parabolisk cylinder eller en hyperbolisk cylinder . I detta fall är punkterna vid oändligheten av C reella (skärningen av ett reellt plan med reella linjer). Således kan de plana sektionerna av Q inte vara cirklar (inte heller ellipser ).

Om Q är en sfär är dess skärning med planet i oändligheten ombilicen, och alla plansektioner är cirklar.

Om Q är en yta av rotation , består dess skärning med ombilicen av ett par komplexa konjugerade punkter (som är dubbla punkter) . Ett verkligt plan innehåller dessa två punkter om och endast om det är vinkelrätt mot rotationsaxeln. Således är de cirkulära sektionerna de plana sektionerna med ett plan vinkelrätt mot axeln, som har minst två reella punkter.

I de andra fallen består skärningspunkten mellan Q och ombilicen av två olika par av komplexa konjugerade punkter. Eftersom C är en kurva av grad två, består dess skärning med planet i oändligheten av två punkter, möjligen lika. Kurvan C är alltså en cirkel, om dessa två punkter är ett av dessa två par av komplexa konjugerade punkter på ombilicen. Vart och ett av dessa par definierar en reell linje (som går genom punkterna), som är skärningspunkten mellan P och planet i oändligheten. Således har man en cirkulär sektion om och endast C har minst två reella punkter och P innehåller en av dessa linjer i oändligheten (det vill säga om P är parallell med en av två riktningar som definieras av dessa linjer i oändligheten).

Bestämning av cirkulära sektioner av en quadric

För att hitta planen, som innehåller cirkulära sektioner av en given quadric, använder man följande påståenden:

(S:) Om de gemensamma punkterna för en quadric med en sfär finns i ett par plan, så består skärningskurvan av två cirklar.

(P:) Om skärningspunkten mellan ett plan och en kvadratisk är en cirkel, så skär alla parallella plan, som innehåller minst två punkter av kvadraten, också kvadraten i en cirkel.

Därför är strategin för detektering av cirkulära sektioner:

1) Hitta en sfär som skär kvadriken i ett par plan och

2) Planen som är parallella med de detekterade levererar de återstående cirkulära sektionerna.

Tri-axiell ellipsoid

tri-axiell ellipsoid med cirkulära sektioner (blå och grön) och hjälpsfären (röd), som skär fyrkanten i de blå cirklarna

Ellipsoid som skärs av sfärer: $c<{\color {seagreen}r_{1}}<{\color {blå}b}<{\color {lila}r_{ 2}}<a$

För ellipsoiden med ekvation

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b ^{2}}}+{\frac {z^{2}}{c^{2}}}=1$

och halvaxlarna $a>b>c>0$ en använder en hjälpsfär med ekvation

$x^{2}+y^{2}+z^{2}=r^{2}\ .$

Sfärens radie måste väljas så att skärningen med ellipsoiden finns i två plan genom origo. Multiplikation av ellipsoidens ekvation med $r^{2}$ och subtrahera sfärens ekvation ger:

$\left({\frac {r^{2}}{a^{2}}}-1\right)\;x^{2}+\left({\frac {r^{2}} {b^{2}}}-1\höger)\;y^{2}+\vänster({\frac {r^{2}}{c^{2}}}-1\höger)\;z ^{2}=0\ .$

Denna ekvation beskriver ett par plan, om en av de 3 koefficienterna är noll. I fallet med $\ r=a\$ eller $\ r=c\$ uppfylls ekvationen endast av antingen x-axeln eller z-axeln. Endast i fallet med $\ r=b\$ får man ett par plan med ekvation

• $\left({\frac { b^{2}}{a^{2}}}-1\höger)\;x^{2}+\left({\frac {b^{2}}{c^{2}}}-1 \right)\;z^{2}=0\ \quad \leftrightarrow \quad z=\pm {\tfrac {c}{a}}{\sqrt {\tfrac {a^{2}-b^{2 }}{b^{2}-c^{2}}}}\;x\ ,$

eftersom endast i detta fall de återstående koefficienterna har olika tecken (beroende på: ${\displaystyle a>b>c} )$ .

Diagrammet ger ett intryck av vanligare skärningspunkter mellan en sfär och en ellipsoid och framhäver det exceptionella cirkulära fallet (blått).

Om värdena för halvaxlarna närmar sig, närmar sig de två pennorna av plan (och cirklar) antingen. För $a=b$ är alla plan ortogonala mot z-axeln (rotationsaxeln).

Bevis på egenskap (P): Att vrida ellipsoiden runt y-axeln så att en av de två cirklarna (blå) ligger i xy-planet resulterar i en ny ekvation för ellipsoiden:

$Ax^{2}+By^{2}+Cz^{2}+D{\color {red}xz}=E$

För $z=0$ får man ${\displaystyle Ax^{2}+By^{2}=E} ,$ vilket måste vara ekvationen för en cirkel. Detta är bara sant om $A=B\neq 0,\ E>0$ . Skärningen av ellipsoiden med ett plan med ekvation ${\displaystyle z=z_{0}} ,$ (parallellt med xy-planet) har ekvationen

$A(x^{2}+y^{2})+Dz_{0}x=E-Cz_{0}^{ 2}$ .

Denna ekvation beskriver en cirkel eller en punkt eller den tomma mängden. Cirkelns centrum och radie kan hittas när du fyller i kvadraten .

Elliptisk hyperboloid av ett ark

hyperboloid av ett ark

För hyperboloiden av ett ark med ekvation

${\frac {x^{2}}{a^{2}}}+{\frac {y ^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1\ ,\quad a>b\ ,c>0$

analogt får man för skärningspunkten med sfären $\ x^{2}+y^{2}+z^{2}=r^{2}\$ den ekvation

$\left({\frac {r^{2}}{a^{2}}}-1\right)\;x^{2}+\left({\frac {r^{2}} {b^{2}}}-1\höger)\;y^{2}-\vänster({\frac {r^{2}}{c^{2}}}+1\höger)\;z ^{2}=0\ .$

Endast för $\ r=a\$ får man ett par plan:

$\left({\frac { a^{2}}{b^{2}}}-1\höger)\;y^{2}-\left({\frac {a^{2}}{c^{2}}}+1 \right)\;z^{2}=0\ \quad \leftrightarrow \quad z=\pm {\frac {c}{b}}{\sqrt {\frac {a^{2}-b^{2 }}{a^{2}+c^{2}}}}\;y\ ,\$

Elliptisk cylinder

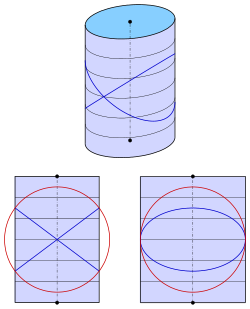
elliptisk cylinder

För den elliptiska cylindern med ekvation

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b ^{2}}}=1\ ,\quad a>b\ ,$

man får ekvationen

$\left({\frac {r^{2}}{a^{2}}}-1\right)\;x^{2}+\left({\frac {r^{2}} {b^{2}}}-1\höger)\;y^{2}-z^{2}=0\ .$

Endast för $\ r=a\$ får man ett par plan:

$\left({\frac {a^{2}}{b^{2}}}-1\right)\;y^{2}-z^{2}=0\ \quad \leftrightarrow \ quad z=\pm {\frac {\sqrt {a^{2}-b^{2}}}{b}}\;y\ .\$

Elliptisk paraboloid

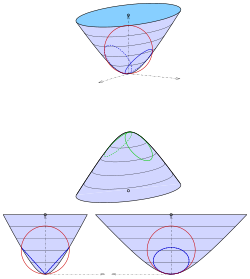
elliptisk paraboloid

För den elliptiska paraboloiden med ekvation

$ax^{2}+by^{2}-z=0\ ,\quad a{\color {red}{<}}b\ ,$

man väljer en sfär som innehåller vertex (ursprung) och med centrum på axeln (z-axel):

$x^{2}+y^{2}+(zr)^{2}=r^{2}\quad \leftrightarrow \quad x^{2}+y^{2}+z^{2 }-2rz=0\ .$

Efter eliminering av de linjära delarna får man ekvationen

$(2ra-1)\;x^{2}+(2rb-1)\;y^{2}-z^{2}=0\ .$

Endast för $r={\tfrac {1}{2a}}$ får man ett par plan:

$\left({\frac {b}{a}}-1\right)\;y^{2}-z^{2}=0\quad \leftrightarrow \quad z=\pm {\sqrt { \frac {ba}{a}}}\;y\ .\$

Elliptisk hyperboloid av två ark

elliptisk hyperboloid av två ark

Hyperboloiden av två ark med ekvation

$-{\frac {x^{2}}{a^{2}}}-{\ frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1\ ,\quad a>b\ ,\ c>0 \ ,$

skiftas först så att en vertex är origo (s. diagram):

$-{\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}+{\frac {(z+c )^{2}}{c^{2}}}=1\quad \leftrightarrow \quad \ -{\frac {x^{2}}{a^{2}}}-{\frac {y^{ 2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}+{\frac {2z}{c}}=0\ .$

Analogt med paraboloidfallet väljer man en sfär som innehåller origo med centrum på z-axeln:

$x^{2}+y^{2}+(zr)^{2}=r^{2}\quad \leftrightarrow \quad x^{2}+y^{2}+z^{2 }-2zr=0\ .$

Efter eliminering av de linjära delarna får man ekvationen

$\left(-{\frac {r}{a^{2}}}+{\frac {1}{c}}\right)\;x^{2}+\left(-{\frac {r}{b^{2}}}+{\frac {1}{c}}\right)\;y^{2}+\left({\frac {r}{c^{2}}} +{\frac {1}{c}}\right)z^{2}=0\ .$

Endast för $r={\tfrac {a^{2}}{c}}$ får man ett par plan:

$\left(-{\frac {a^{2}}{b^{2}c}}+{\frac {1}{c}}\right)\;y^{2}+\left ({\frac {a^{2}}{c^{3}}}+{\frac {1}{c}}\right)\;z^{2}=0\ \quad \leftrightarrow \quad z =\pm {\frac {c}{b}}{\sqrt {\frac {a^{2}-b^{2}}{a^{2}+c^{2}}}}\;y \ .$

Elliptisk kon

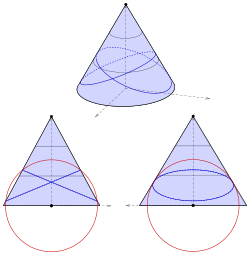
elliptisk kon

Den elliptiska konen med ekvation

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}} {b^{2}}}-z^{2}=0\ ,\quad a>b\ ,$

skiftas så att vertex inte är origo (s. diagram):

${\frac {x^{2}}{ a^{2}}}+{\frac {y^{2}}{b^{2}}}-(z-1)^{2}=0\quad \leftrightarrow \quad {\frac {x^ {2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-z^{2}+2z=1.$

Nu är en sfär med centrum vid utgången lämplig:

$x^{2}+y^{2}+z^{2}=r^{2}\ .$

Eliminering av $x^{2}$ ger:

$({\frac {a^{2}}{b^{2}}}-1)\;y^{2}-(1+a^{2})\;z^{2}+ 2a^{2}z=a^{2}-r^{2}\ .$

I det här fallet får du:

${\frac {a^{2}-b^{2}}{b^{2}}}\;y^{2}-(1+a^{2})\left(z-{ \frac {a^{2}}{1+a^{2}}}\right)^{2}=a^{2}-{\frac {a^{4}}{1+a^{2 }}}-r^{2}\ .$

För att få ekvationen för ett par plan måste den högra delen av ekvationen vara noll, vilket är sant för $r={\tfrac {a}{\sqrt {1+a^{2}}}}\ .$ Lösningen för z ger:

$z={\frac {a^{2}}{1+a^{2}}}\pm {\frac {1}{b}}{\sqrt {\frac {a^{2}- b^{2}}{1+a^{2}}}}\;y\ .$

•   HF Baker: Principles of Geometry, Volym 3 , Cambridge University Press, 2010, ISBN 978-1-108-01779-4 .
•   DMY Sommerville: Analytical Geometry of Three Dimensions , Cambridge University Press, 1959, ISBN 978-1-316-60190-7 , sid. 204.
• KP Grotemeyer: Analytische geometri. Göschen-Verlag, 1962, sid. 143.
•   H. Scheid, W. Schwarz: Elemente der Linearen Algebra und der Analysis. Spektrum, Heidelberg, 2009, ISBN 978-3-8274-1971-2 , sid. 132.

externa länkar

• H. Wiener, P. Treutlein: Modeller av en tri-axiell ellipsoid och en elliptisk paraboloid med hjälp av cirkulära sektioner (se sid. 15) [ 1] (PDF).