Belysningsproblem

Roger Penroses lösning av belysningsproblemet med hjälp av elliptiska bågar (blå) och raka linjesegment (grön), med 3 positioner av den enda ljuskällan (röd fläck). De lila korsen är fokus för de större bågarna. Tända och oupplysta områden visas i gult respektive grått.

Belysningsproblem är en klass av matematiska problem som studerar belysningen av rum med spegelväggar av punktljuskällor .

Ursprunglig formulering

Den ursprungliga formuleringen tillskrevs Ernst Straus på 1950-talet och har lösts. Straus frågade om ett rum med spegelväggar alltid kan belysas av en enda punkts ljuskälla, vilket möjliggör upprepad reflektion av ljus från spegelväggarna. Alternativt kan frågan ställas som att om ett biljardbord kan konstrueras i vilken form som helst, finns det en form möjlig så att det finns en punkt där det är omöjligt att träffa biljardbollen vid en annan punkt, förutsatt att bollen är punktliknande och fortsätter i det oändliga snarare än att stanna på grund av friktion .

Penrose obelysbart rum

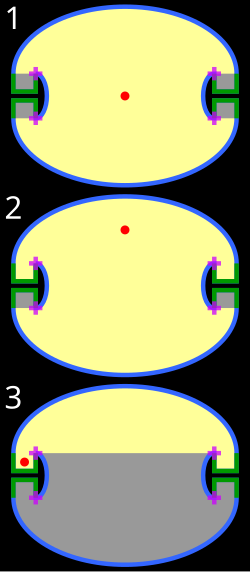
Det ursprungliga problemet löstes först 1958 av Roger Penrose med hjälp av ellipser för att bilda Penrose obelysbara rum . Han visade att det finns ett rum med böjda väggar som alltid måste ha mörka områden om endast upplyst av en enda punktkälla.

Polygonala rum

Lösningar på belysningsproblemet av George W. Tokarsky (26 sidor) och David Castro (24 sidor)

Detta problem löstes också för polygonala rum av George Tokarsky 1995 för 2 och 3 dimensioner, vilket visade att det finns ett obelyst polygonalt 26-sidigt rum med en "mörk fläck" som inte är upplyst från en annan punkt i rummet, till och med tillåter för upprepade reflektioner. Dessa var sällsynta fall, när ett ändligt antal mörka punkter (snarare än regioner) är obelysbara endast från en fast position av punktkällan.

1997 lades två olika 24-sidiga rum med samma egenskaper fram av George Tokarsky och David Castro var för sig.

1995 hittade Tokarsky det första polygonala obelysbara rummet som hade 4 sidor och två fasta gränspunkter. 2016 visade Samuel Lelièvre, Thierry Monteil och Barak Weiss att en ljuskälla i ett polygonalt rum vars vinklar (i grader) alla är rationella tal kommer att belysa hela polygonen, möjligen med undantag för ett ändligt antal punkter. 2019 stärktes detta av Amit Wolecki som visade att för varje sådan polygon är antalet punkter som inte lyser upp varandra ändligt.

Det första polygonala Tokarsky oupplysta rummet med 4 sidor, 1995. En video som visar vägen för en biljardboll i detta rum.


The Original Tokarsky Unilluminable Room with 24 pages, 1995. En video som visar vägen för en biljardboll i detta rum.
Ett udda Tokarsky obelysbart rum med 27 sidor, 1996. En video som visar vägen för en biljardboll i det här rummet.

externa länkar

Hämtad från " https://en.wikipedia.org/w/index.php?title=Illumination_problem&oldid=1137682013 "