Adaptiv resonans teori

Adaptiv resonansteori ( ART ) är en teori utvecklad av Stephen Grossberg och Gail Carpenter om aspekter av hur hjärnan bearbetar information . Den beskriver ett antal neurala nätverksmodeller som använder övervakade och oövervakade inlärningsmetoder och tar upp problem som mönsterigenkänning och förutsägelse.

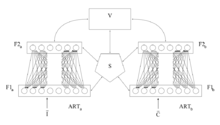
Den primära intuitionen bakom ART-modellen är att objektidentifiering och -igenkänning i allmänhet sker som ett resultat av interaktionen mellan observatörens förväntningar från "uppifrån och ner" och sensorisk information "nedifrån och upp" . Modellen postulerar att "top-down" förväntningar tar formen av en minnesmall eller prototyp som sedan jämförs med de faktiska egenskaperna hos ett objekt som detekteras av sinnena. Denna jämförelse ger upphov till ett mått på kategoritillhörighet. Så länge som denna skillnad mellan sensation och förväntan inte överstiger en inställd tröskel som kallas 'vigilance parameter', kommer det avkända objektet att betraktas som en medlem av den förväntade klassen. Systemet erbjuder alltså en lösning på problemet med 'plasticitet/stabilitet', det vill säga problemet med att skaffa ny kunskap utan att störa befintlig kunskap som även kallas inkrementellt lärande .

Inlärningsmodell

Grundläggande ART-struktur

Det grundläggande ART-systemet är en oövervakad inlärningsmodell . Den består vanligtvis av ett jämförelsefält och ett igenkänningsfält som består av neuroner , en vaksamhetsparameter (igenkänningströskel) och en återställningsmodul .

  • Jämförelsefältet tar en indatavektor (en endimensionell array av värden) och överför den till sin bästa matchning i igenkänningsfältet.
    • Dess bästa matchning är den enda neuron vars uppsättning vikter (viktvektor) mest matchar ingångsvektorn.
  • Varje igenkänningsfältsneuron matar ut en negativ signal (proportionell mot den neurons kvalitet av matchning med ingångsvektorn) till var och en av de andra igenkänningsfältsneuronerna och hämmar sålunda deras utmatning.
    • På detta sätt uppvisar igenkänningsfältet lateral inhibering , vilket gör att varje neuron i det kan representera en kategori till vilken ingångsvektorer klassificeras.
  • Efter att ingångsvektorn har klassificerats jämför återställningsmodulen styrkan på igenkänningsmatchningen med vaksamhetsparametern.
    • Om vaksamhetsparametern övervinns (dvs. ingångsvektorn är inom det normala intervallet som ses på tidigare indatavektorer), börjar träningen:
      • Vikterna för den vinnande igenkänningsneuronen justeras mot egenskaperna hos ingångsvektorn
    • Annars, om matchningsnivån är under vaksamhetsparametern (dvs. indatavektorns matchning ligger utanför det normala förväntade intervallet för den neuronen) inhiberas den vinnande igenkänningsneuronen och en sökprocedur utförs.
      • I denna sökprocedur inaktiveras igenkänningsneuroner en efter en av återställningsfunktionen tills vaksamhetsparametern övervinns av en igenkänningsmatchning.
        • I synnerhet, vid varje cykel av sökproceduren väljs den mest aktiva igenkänningsneuronen och stängs sedan av, om dess aktivering är under vaksamhetsparametern
        • (observera att det därmed frigör de återstående igenkänningsneuronerna från sin hämning).
    • Om ingen engagerad igenkänningsneurons matchning övervinner vaksamhetsparametern, är en oengagerad neuron engagerad och dess vikter justeras för att matcha ingångsvektorn.
  • Vaksamhetsparametern har betydande inverkan på systemet: högre vaksamhet ger mycket detaljerade minnen (många, finkorniga kategorier), medan lägre vaksamhet resulterar i mer allmänna minnen (färre, mer allmänna kategorier).

Träning

Det finns två grundläggande metoder för att träna ART-baserade neurala nätverk: långsamt och snabbt. I den långsamma inlärningsmetoden beräknas graden av träning av igenkänningsneuronens vikter mot ingångsvektorn till kontinuerliga värden med differentialekvationer och är således beroende av hur lång tid ingångsvektorn presenteras. Med snabb inlärning används algebraiska ekvationer för att beräkna graden av viktjusteringar som ska göras, och binära värden används. Även om snabb inlärning är effektiv och effektiv för en mängd olika uppgifter, är den långsamma inlärningsmetoden mer biologiskt rimlig och kan användas med kontinuerliga tidsnätverk (dvs när indatavektorn kan variera kontinuerligt).

Typer

ART 1 är den enklaste varianten av ART-nätverk, som endast accepterar binära ingångar. ART 2 utökar nätverkskapaciteten för att stödja kontinuerliga ingångar. ART 2-A är en strömlinjeformad form av ART-2 med en drastiskt accelererad körtid och med kvalitativa resultat som endast sällan är sämre än den fullständiga ART-2-implementeringen. ART 3 bygger på ART-2 genom att simulera rudimentär neurotransmittorreglering av synaptisk aktivitet genom att införliva simulerade natrium- (Na+)- och kalcium- (Ca2+)-jonkoncentrationer i systemets ekvationer, vilket resulterar i ett mer fysiologiskt realistiskt sätt att delvis hämma kategorier som utlöser återställningar av missmatchning .

ARTMAP översikt

ARTMAP, även känd som Predictive ART , kombinerar två något modifierade ART-1 eller ART-2 enheter till en övervakad inlärningsstruktur där den första enheten tar indata och den andra enheten tar rätt utdata, sedan används för att göra minsta möjliga justering av vaksamhetsparametern i den första enheten för att göra rätt klassificering.

Fuzzy ART implementerar fuzzy logik i ART:s mönsterigenkänning, vilket förbättrar generaliserbarheten. En valfri (och mycket användbar) funktion hos fuzzy ART är komplementkodning, ett sätt att införliva frånvaron av funktioner i mönsterklassificeringar, vilket går långt för att förhindra ineffektiv och onödig kategorispridning. De tillämpade likhetsmåtten baseras på L1-normen . Fuzzy ART är känt för att vara mycket känslig för brus.

Fuzzy ARTMAP är bara ARTMAP som använder fuzzy ART-enheter, vilket resulterar i en motsvarande ökning av effektiviteten.

Simplified Fuzzy ARTMAP (SFAM) utgör en starkt förenklad variant av fuzzy ARTMAP dedikerad till klassificeringsuppgifter .

Gaussisk ART och Gaussisk ARTMAP använder Gaussiska aktiveringsfunktioner och beräkningar baserade på sannolikhetsteori. Därför har de en viss likhet med Gaussiska blandningsmodeller . I jämförelse med fuzzy ART och fuzzy ARTMAP är de mindre känsliga för brus. Men stabiliteten hos inlärda representationer minskar vilket kan leda till kategorispridning i öppna lärandeuppgifter.

Fusion ART och relaterade nätverk utökar ART och ARTMAP till flera mönsterkanaler. De stöder flera inlärningsparadigm, inklusive oövervakat lärande, övervakat lärande och förstärkningsinlärning.

TopoART kombinerar fuzzy ART med topologiinlärningsnätverk som den växande neurala gasen . Dessutom lägger den till en brusreduceringsmekanism. Det finns flera härledda neurala nätverk som utökar TopoART till ytterligare inlärningsparadigm.

Hypersphere ART och Hypersphere ARTMAP är nära besläktade med fuzzy ART respektive fuzzy ARTMAP. Men eftersom de använder en annan typ av kategorirepresentation (nämligen hypersfärer), kräver de inte att deras input normaliseras till intervallet [0, 1]. De tillämpar likhetsmått baserat på L2-normen .

LAPART The Laterally Primed Adaptive Resonance Theory (LAPART) neurala nätverk kopplar två Fuzzy ART-algoritmer för att skapa en mekanism för att göra förutsägelser baserade på inlärda associationer. Kopplingen av de två Fuzzy ARTs har en unik stabilitet som gör att systemet snabbt konvergerar mot en tydlig lösning. Dessutom kan den utföra logisk slutledning och övervakad inlärning liknande fuzzy ARTMAP.

Kritik

Det har noterats att resultaten av Fuzzy ART och ART 1 (dvs. de inlärda kategorierna) är kritiskt beroende av i vilken ordning träningsdata behandlas. Effekten kan minskas till viss del genom att använda en långsammare inlärningshastighet, men är närvarande oavsett storleken på indatauppsättningen. Därför har Fuzzy ART och ART 1 uppskattningar inte den statistiska egenskapen konsistens . Detta problem kan betraktas som en bieffekt av de respektive mekanismerna som säkerställer stabilt lärande i båda nätverken.

Mer avancerade ART-nätverk som TopoART och Hypersphere TopoART som sammanfattar kategorier till kluster kan lösa detta problem eftersom formerna på klustren inte beror på ordningen för skapande av de associerade kategorierna. (jfr fig. 3(g, h) och fig. 4 av )

  Wasserman, Philip D. (1989), Neural computing: theory and practice, New York: Van Nostrand Reinhold, ISBN 0-442-20743-3

externa länkar

Hämtad från " https://en.wikipedia.org/w/index.php?title=Adaptive_resonance_theory&oldid=1131192463 "