AVL-träd

AVL-träd
Typ	Träd
Uppfunnet	1962
Uppfunnet av	Georgy Adelson-Velsky och Evgenii Landis
Komplexiteter i stor O-notation
Rymdkomplexitet Plats ${\text{Θ}}(n)$ Tidskomplexitet Fungera Amorteras Värsta fall Sök ${\text{Θ}}(\log n)$ ${\text{O}}(\log n)$ Föra in ${\text{Θ}}(\log n)$ ${\text{O}}(\log n)$ Radera ${\text{Θ}}(\log n)$ ${\text{O}}(\log n)$

Animation som visar infogningen av flera element i ett AVL-träd. Den inkluderar vänster, höger, vänster-höger och höger-vänster rotationer.

Fig. 1: AVL-träd med balansfaktorer (grön)

Inom datavetenskap är ett AVL-träd (uppkallat efter uppfinnarna A delson -V elsky och L andis) ett självbalanserande binärt sökträd . Det var den första sådan datastruktur som uppfanns. I ett AVL-träd skiljer sig höjderna av de två underordnade underträden av någon nod med högst en; om de vid något tillfälle skiljer sig med mer än en, görs ombalansering för att återställa denna egenskap. Uppslagning, infogning och radering tar alla O (log n ) tid i både genomsnittliga och värsta fall, där $n$ är antalet noder i trädet före operationen. Infogningar och borttagningar kan kräva att trädet balanseras om av en eller flera trädrotationer .

AVL-trädet är uppkallat efter dess två sovjetiska uppfinnare, Georgy Adelson-Velsky och Evgenii Landis , som publicerade det i sin tidning från 1962 "An algorithm for the organisation of information".

AVL-träd jämförs ofta med röd-svarta träd eftersom båda stöder samma uppsättning operationer och tar ${\text{O}}(\log n)$ tid för de grundläggande operationerna. För uppslagsintensiva tillämpningar är AVL-träd snabbare än rödsvarta träd eftersom de är mer strikt balanserade. I likhet med röd-svarta träd är AVL-träd höjdbalanserade. Båda är i allmänhet varken viktbalanserade eller $\mu$ -balanserade för någon $\mu \leq {\tfrac {1}{2}}$ ; det vill säga syskonnoder kan ha enormt olika antal ättlingar.

Definition

Balansfaktor

I ett binärt träd definieras balansfaktorn för en nod X som höjdskillnaden

${\text{BF}}(X):={\text{Höjd}}({\text{RightSubtree} }(X))-{\text{Höjd}}({\text{LeftSubtree}}(X))$

av dess två underträd. Ett binärt träd definieras som ett AVL-träd om det är invariant

${\text{BF}}(X)\in {\{-1,0,1\}}$

gäller för varje nod X i trädet.

En nod X med ${\text{BF}}(X)<0$ kallas "vänstertung", en med ${\text{BF}} (X)>0$ kallas "höger-tung", och en med ${\text{BF}}(X)=0$ kallas ibland helt enkelt "balanserad".

Egenskaper

Balansfaktorer kan hållas uppdaterade genom att känna till tidigare balansfaktorer och höjdförändringen – det är inte nödvändigt att veta den absoluta höjden. För att hålla AVL-balansinformationen räcker två bitar per nod.

Höjden $h$ (räknas som det maximala antalet nivåer) för ett AVL-träd med $n$ -noder ligger i intervallet:

$\log _{2}(n+1)\leq h<\log _{\varphi }(n+2 )+b$

där $\varphi :={\tfrac {1+{\sqrt {5}}}{2}}\ca 1,618$ är det gyllene snittet och ${\displaystyle b:={\frac {\log _{2}5}{2\log _{2}\varphi }}-2\approx \;-0.3277.} Detta beror på att ett AVL-träd med$ höjden ${ \displaystyle h}$ innehåller minst $F_{h}-1$ noder där $\{F_{n}\}_{n\in \mathbb {N } }$ är Fibonacci-sekvensen med frövärdena $F_{1}=F_{2}=1.$

Operationer

Skrivskyddade operationer för ett AVL-träd innebär att utföra samma åtgärder som skulle utföras på ett obalanserat binärt sökträd, men modifieringar måste observera och återställa höjdbalansen för underträden.

Sökande

Att söka efter en specifik nyckel i ett AVL-träd kan göras på samma sätt som för alla balanserade eller obalanserade binära sökträd . För att sökningen ska fungera effektivt måste den använda en jämförelsefunktion som upprättar en total ordning (eller åtminstone en total förbeställning ) på uppsättningen nycklar. Antalet jämförelser som krävs för framgångsrik sökning begränsas av höjden h och för misslyckad sökning är mycket nära h , så båda är i O(log n ) .

Traversering

Som en skrivskyddad operation fungerar genomgången av ett AVL-träd på samma sätt som på vilket annat binärt träd som helst. Att utforska alla n noder i trädet besöker varje länk exakt två gånger: ett nedåtgående besök för att gå in i underträdet som är rotat av den noden, ett annat besök uppåt för att lämna den nodens underträd efter att ha utforskat det.

När en nod har hittats i ett AVL-träd, kan nästa eller föregående nod nås i avskriven konstant tid. Vissa tillfällen av att utforska dessa "nära" noder kräver att man korsar upp till h ∝ log( n ) länkar (särskilt när man navigerar från bladet längst till höger i rotens vänstra underträd till roten eller från roten till bladet längst till vänster i rotens högra underträd; i AVL-trädet i figur 1 tar navigeringen från nod P till noden Q näst till höger 3 steg). Eftersom det finns n −1 länkar i vilket träd som helst, är den amorterade kostnaden 2×( n −1)/ n , eller ungefär 2.

Föra in

När du infogar en nod i ett AVL-träd följer du till en början samma process som att infoga i ett binärt sökträd . Om trädet är tomt, infogas noden som trädets rot. Om trädet inte är tomt, går vi ner i roten och går rekursivt ner i trädet och söker efter platsen för att infoga den nya noden. Denna genomgång styrs av jämförelsefunktionen. I det här fallet ersätter noden alltid en NULL-referens (vänster eller höger) för en extern nod i trädet, dvs noden görs antingen till vänster- eller höger-underordnad till den externa noden.

Efter denna infogning, om ett träd blir obalanserat, är endast förfäder till den nyligen infogade noden obalanserade. Detta beror på att endast dessa noder har sina underträd ändrade. Så det är nödvändigt att kontrollera var och en av nodens förfäder för överensstämmelse med AVL-trädens invarianter: detta kallas "retracing". Detta uppnås genom att beakta balansfaktorn för varje nod.

Eftersom höjden på ett AVL-underträd med en enstaka infogning inte kan öka med mer än en, kommer den temporära balansfaktorn för en nod efter en insättning att ligga i intervallet [ –2,+2]. För varje kontrollerad nod, om den temporära balansfaktorn förblir i intervallet från –1 till +1 är endast en uppdatering av balansfaktorn och ingen rotation nödvändig. Men om den temporära balansfaktorn är ±2, är underträdet som är rotat vid denna nod AVL-obalanserat, och en rotation behövs. Med insättning som koden nedan visar, balanserar den adekvata rotationen omedelbart trädet perfekt.

I figur 1, genom att infoga den nya noden Z som ett barn till nod X, ökar höjden på det underträdet Z från 0 till 1.

Invariant av retracing-slingan för en infogning

Höjden på underträdet som är rotat av Z har ökat med 1. Det är redan i AVL-form.

Exempelkod för en infogningsoperation

0 0 0 0 0 0 0 0 för ( X = parent ( Z ); X != null ; X = parent ( Z )) { // Loop (eventuellt upp till roten) // BF(X) måste uppdateras: if ( Z == höger_barn ( X )) { // Det högra underträdet ökar om ( BF ( X ) > ) { // X är höger-tungt // ==> den tillfälliga BF(X) == +2 // = => ombalansering krävs. G = förälder ( X ); // Spara förälder till X runt rotationer om ( BF ( Z ) < ) // Höger Vänster Case (se figur 3) N = rotate_RightLeft ( X , Z ); // Dubbelrotation: Höger(Z) sedan Vänster(X) annars // Höger Höger Case (se figur 2) N = rotate_Left ( X , Z ); // Enkel rotation Left(X) // Efter rotation adapt parent link } else { if ( BF ( X ) < ) { BF ( X ) = ; // Z:s höjdökning absorberas vid X. break ; // Lämna loopen } BF ( X ) = + 1 ; Z = X ; // Höjd(Z) ökar med 1 fortsätt ; } } else { // Z == left_child(X): det vänstra underträdet ökar om ( BF ( X ) < ) { // X är vänstertungt // ==> den tillfälliga BF(X) == -2 / / ==> ombalansering krävs. G = förälder ( X ); // Spara förälder till X runt rotationer if ( BF ( Z ) > ) // Left Right Case N = rotate_LeftRight ( X , Z ); // Dubbelrotation: Left(Z) then Right(X) else // Left Left Case N = rotate_Right ( X , Z ); // Enkelrotation Höger(X) // Efter rotation anpassa föräldralänk } else { if ( BF ( X ) > ) { BF ( X ) = ; // Z:s höjdökning absorberas vid X. break ; // Lämna loopen } BF ( X ) = -1 ; Z = X ; // Höjd(Z) ökar med 1 fortsätt ; } } // Efter en rotation anpassa föräldralänk: // N är den nya roten av det roterade underträdet // Höjd ändras inte: Höjd(N) == gammal Höjd(X) förälder ( N ​​) = G ; if ( G != null ) { if ( X == left_child ( G )) left_child ( G ) = N ; annars right_child ( G ) = N ; } annat träd -> rot = N ; // N är den nya roten av det totala trädbrottet ; // Det finns inget fall genom, bara brytning; eller fortsätt; } // Om inte slingan lämnas via break, ökar höjden på det totala trädet med 1.

För att uppdatera balansfaktorerna för alla noder, observera först att alla noder som kräver korrigering ligger från barn till förälder längs vägen för det infogade bladet. Om ovanstående procedur tillämpas på noder längs denna väg, med början från bladet, kommer varje nod i trädet åter att ha en balansfaktor på -1, 0 eller 1.

Återgången kan stoppas om balansfaktorn blir 0, vilket innebär att höjden på det underträdet förblir oförändrad.

Om balansfaktorn blir ±1 så ökar höjden på underträdet med ett och återgången måste fortsätta.

Om balansfaktorn tillfälligt blir ±2 måste detta repareras genom en lämplig rotation varefter underträdet har samma höjd som tidigare (och dess rot balansfaktorn 0).

Tiden som krävs är O(log n ) för uppslagning, plus maximalt O(log n ) spårningsnivåer ( O(1) i genomsnitt) på vägen tillbaka till roten, så operationen kan slutföras i O(log n ) tid.

Radera

De preliminära stegen för att ta bort en nod beskrivs i avsnittet Binärt sökträd#Deletion . Där minskar den effektiva raderingen av ämnesnoden eller ersättningsnoden höjden på motsvarande barnträd antingen från 1 till 0 eller från 2 till 1, om den noden hade ett barn.

Med början vid detta underträd är det nödvändigt att kontrollera var och en av förfäderna för överensstämmelse med AVL-trädens invarianter. Detta kallas "retracing".

Eftersom höjden på ett AVL-underträd med en enstaka radering inte kan minska med mer än en, kommer den temporära balansfaktorn för en nod att ligga i intervallet från -2 till +2. Om balansfaktorn förblir i området från −1 till +1 kan den justeras i enlighet med AVL-reglerna. Om det blir ±2 är underträdet obalanserat och måste roteras. (Till skillnad från insättning där en rotation alltid balanserar trädet, efter radering, kan det finnas BF(Z) ≠ 0 (se figur 2 och 3), så att efter lämplig enkel- eller dubbelrotation minskar höjden på det ombalanserade underträdet med en betydelse att trädet måste balanseras om igen på nästa högre nivå.) De olika fallen av rotationer beskrivs i avsnittet Ombalansering .

Invariant av spårningsslingan för en radering

Höjden på underträdet som är rotat av N har minskat med 1. Det är redan i AVL-form.

Exempelkod för en raderingsoperation

0 0 0 0 0 0 0 0 0 för ( X = parent ( N ); X != null ; X = G ) { // Loop (eventuellt upp till roten) G = parent ( X ); // Spara förälder till X runt rotationer // BF(X) har ännu inte uppdaterats! if ( N == left_child ( X )) { // det vänstra underträdet minskar om ( BF ( X ) > ) { // X är höger-tungt // ==> den tillfälliga BF(X) == +2 // ==> ombalansering krävs. Z = höger_barn ( X ); // Syskon till N (2 högre) b = BF ( Z ); if ( b < ) // Höger Vänster Fall (se figur 3) N = rotate_RightLeft ( X , Z ); // Dubbelrotation: Höger(Z) sedan Vänster(X) annars // Höger Höger Case (se figur 2) N = rotate_Left ( X , Z ); // Enkel rotation Left(X) // Efter rotation anpassa föräldralänk } else { if ( BF ( X ) == ) { BF ( X ) = + 1 ; // N:s höjdminskning absorberas vid X. break ; // Lämna loopen } N = X ; BF ( N ) = ; // Höjd(N) minskar med 1 fortsätt ; } } else { // (N == höger_barn(X)): Det högra underträdet minskar om ( BF ( X ) < ) { // X är vänstertungt // ==> den tillfälliga BF(X) == - 2 // ==> ombalansering krävs. Z = vänster_barn ( X ); // Syskon till N (2 högre) b = BF ( Z ); if ( b > ) // Left Right Case N = rotate_LeftRight ( X , Z ); // Dubbelrotation: Left(Z) then Right(X) else // Left Left Case N = rotate_Right ( X , Z ); // Enkelrotation Höger(X) // Efter rotation anpassa föräldralänk } else { if ( BF ( X ) == ) { BF ( X ) = -1 ; // N:s höjdminskning absorberas vid X. break ; // Lämna loopen } N = X ; BF ( N ) = ; // Höjd(N) minskar med 1 fortsätt ; } } // Efter en rotation anpassa överordnad länk: // N är den nya roten av det roterade underträdets överordnade ( N ) = G ; if ( G != null ) { if ( X == left_child ( G )) left_child ( G ) = N ; annars right_child ( G ) = N ; } annat träd -> rot = N ; // N är den nya roten av det totala trädet om ( b == ) break ; // Höjd ändras inte: Lämna slingan // Höjd(N) minskar med 1 (== gammal Höjd(X)-1) } // Om (b != 0) minskar höjden på det totala trädet med 1.

Återgången kan stoppas om balansfaktorn blir ±1 (den måste ha varit 0) vilket betyder att höjden på det underträdet förblir oförändrad.

Om balansfaktorn blir 0 (den måste ha varit ±1) så minskar höjden på underträdet med ett och spårningen måste fortsätta.

Om balansfaktorn tillfälligt blir ±2 måste detta repareras med en lämplig rotation. Det beror på balansfaktorn för syskonen Z (det högre barnträdet i figur 2) om höjden på underträdet minskar med en – och spårningen behöver fortsätta – eller inte ändras (om Z har balansfaktorn 0) och hela trädet är i AVL-form.

Tiden som krävs är O(log n ) för uppslagning, plus maximalt O(log n ) spårningsnivåer ( O(1) i genomsnitt) på vägen tillbaka till roten, så operationen kan slutföras i O(log n ) tid.

Set operationer och bulk operationer

Utöver operationerna för insättning, radering och uppslagning av ett element med ett element har flera uppsättningsoperationer definierats på AVL-träd: union , intersection och set difference . Sedan kan snabba bulkoperationer på infogningar eller borttagningar implementeras baserat på dessa inställda funktioner. Dessa uppsättningsoperationer är beroende av två hjälpoperationer, Split och Join . Med den nya verksamheten kan implementeringen av AVL-träd bli mer effektiv och mycket parallelliserbar.

Funktionen Sammanfoga på två AVL-träd t ₁ och t ₂ och en nyckel k kommer att returnera ett träd som innehåller alla element i t ₁ , t ₂ samt k . Det kräver k är större än alla nycklar i t ₁ och mindre än alla nycklar i t ₂ . Om de två träden skiljer sig åt i höjd med högst en, enkelt en ny nod med vänster underträd t ₁ , rot k och höger underträd t ₂ . Anta annars att t ₁ är högre än t ₂ för mer än en (det andra fallet är symmetriskt). Join följer den högra ryggraden på t ₁ tills en nod c som är balanserad med t ₂ . Vid denna tidpunkt skapas en ny nod med vänster underordnad c , rot k och höger underordnat t _{2 för att ersätta c.} Den nya noden uppfyller AVL-invarianten, och dess höjd är en större än c . Ökningen i höjd kan öka höjden på dess förfäder, vilket möjligen ogiltigförklarar AVL-invarianten för dessa noder. Detta kan fixas antingen med en dubbelrotation om den är ogiltig hos föräldern eller en enkel vänsterrotation om den är ogiltig högre i trädet, i båda fallen återställer höjden för eventuella ytterligare förfädernoder. Anslutning kommer därför att kräva högst två rotationer. Kostnaden för denna funktion är skillnaden mellan höjderna mellan de två ingångsträden.

Pseudokodimplementering för Join-algoritmen

funktion JoinRightAVL(TL , k, TR ) (l, k', c) = exponera(TL ) if ( Höjd (c) <= Höjd( TR )+1) T' = Nod(c, k, T R ) if (Height(T') <= Height(l)+1) then return Node(l, k', T') else return rotateLeft(Node(l, k', rotateRight(T'))) else T' = JoinRightAVL(c, k, TR ) T'' = Nod(l, k', T') if (Height(T') <= Height(l)+1) return T'' annars return rotateLeft( T'') funktion JoinLeftAVL(TL , k, TR ) /* symmetrisk till JoinRightAVL */ function Join( TL , k, TR ) if (Höjd( TL )>Höjd(TR ) +1) returnerar JoinRightAVL(TL , k, TR ) if (Höjd(TR ) >Höjd( TL )+1) returnera JoinLeftAVL(TL , k, TR ) return Node( TL , k, TR ) Här är Height(v) höjden på ett underträd (nod) v . (l,k,r) = expose(v) extraherar v :s vänstra underordnade l , nyckeln k för v :s rot, och det högra barnet r . Node(l,k,r) betyder att skapa en nod av vänster underordnat l , nyckel k , och höger underordnat r .

För att dela upp ett AVL-träd i två mindre träd, de som är mindre än tangenten k , och de som är större än tangenten k , ritar du först en bana från roten genom att infoga k i AVL:n. Efter denna infogning kommer alla värden mindre än k att hittas till vänster om banan, och alla värden större än k kommer att hittas till höger. Genom att använda Join slås alla underträd på vänster sida samman nedifrån och upp med hjälp av tangenter på banan som mellannoder från botten till toppen för att bilda det vänstra trädet, och den högra delen är asymmetrisk. Kostnaden för Split är O(log n ) , ordning efter trädets höjd.

Pseudokodimplementering för Split-algoritmfunktionen
Split (T, k) if (T = noll) return (noll, falsk, noll) (L,m,R) = exponera(T) om (k = m) return (L, sant , R) if (k<m) (L',b,R') = Split(L,k) return (L', b, Join(R', m, R)) if (k>m) (L ',b,R') = Split(R, k) return (Gå med(L, m, L'), b, R'))

Unionen av två AVL-träd t ₁ och t ₂ som representerar mängderna A och B , är en AVL t som representerar A ∪ B .

Pseudokodimplementering för unionens algoritm

funktion Union(t 1 , t 2 ): om t 1 = noll: returnera t 2 om t 2 = noll: returnera t 1 (t < , b, t > ) = Split(t 2 , t 1 .root) returnera Gå med (Union(vänster(t 1 ), t < ), t 1 .root, Union(höger(t 1 ), t > )) Här antas Split returnera två träd: ett som håller tangenterna minus dess inmatningsnyckel, ett som håller de större tangenterna. (Algoritmen är oförstörande , men det finns en destruktiv version på plats också.)

Algoritmen för korsning eller skillnad är liknande, men kräver Join2- hjälparrutinen som är samma som Join men utan mitttangenten. Baserat på de nya funktionerna för union, korsning eller differens kan antingen en nyckel eller flera nycklar infogas i eller raderas från AVL-trädet. Eftersom Split anropar Join men inte hanterar balanseringskriterierna för AVL-träd direkt, brukar en sådan implementering kallas den "join-baserade" implementeringen .

Komplexiteten för var och en av union, skärningspunkt och skillnad är ${\text{O}}\left(m\log \left({n \over m}+1 \right)\right)$ för AVL-träd i storlekarna $m$ och $n\;(\geq m)$ . Ännu viktigare, eftersom de rekursiva anropen till union, korsning eller skillnad är oberoende av varandra, kan de utföras parallellt med ett parallellt djup ${\text{O}}(\ log m\log n)$ . När $m=1$ har den kopplingsbaserade implementeringen samma beräknings-DAG som insättning och borttagning av enstaka element.

Återbalansering

Om höjdskillnaden mellan två underträd under en modifieringsoperation ändras, kan detta, så länge den är < 2, reflekteras av en anpassning av balansinformationen hos föräldern. Under infogning och borttagning kan en (tillfällig) höjdskillnad på 2 uppstå, vilket innebär att det överordnade underträdet måste "ombalanseras". De givna reparationsverktygen är de så kallade trädrotationerna , eftersom de flyttar nycklarna endast "vertikalt", så att den ("horisontella") sekvensen av nycklarna i sin ordning bevaras helt (vilket är väsentligt för ett binärt sökträd ).

Låt X vara den nod som har en (tillfällig) balansfaktor på −2 eller +2. Dess vänstra eller högra underträd modifierades. Låt Z vara det högre barnet (se figur 2 och 3). Observera att båda barnen är i AVL-form genom induktionshypotes .

Vid insättning har denna insättning hänt ett av Z:s barn på ett sätt att Z:s längd har ökat. Vid radering har denna radering hänt syskonen t ₁ till Z på ett sätt så att t ₁ :s höjd som redan är lägre har minskat. (Detta är det enda fallet där Z:s balansfaktor också kan vara 0.)

Det finns fyra möjliga varianter av överträdelsen:

	Eller hur	⟹ Z är en rättighet	barn till sin förälder X och BF(Z) ≥ 0
	Vänster Vänster	⟹ Z är en vänster	barn till dess förälder X och BF(Z) ≤ 0
	Höger vänster	⟹ Z är en rättighet	barn till dess förälder X och BF(Z) < 0
	Vänster höger	⟹ Z är en vänster	barn till dess förälder X och BF(Z) > 0

Och ombalanseringen utförs annorlunda:

	Eller hur	⟹ X balanseras om med a	enkel	rotation rotate_Left	(se figur 2)
	Vänster Vänster	⟹ X balanseras om med a	enkel	rotation rotate_Right	(spegelbild av figur 2)
	Höger vänster	⟹ X balanseras om med a	dubbel	rotation rotate_RightLeft	(se figur 3)
	Vänster höger	⟹ X balanseras om med a	dubbel	rotation rotate_LeftRight	(spegelbild av figur 3)

Därmed betecknas situationerna som CB , där C (= barnriktning) och B (= balans) kommer från mängden { Vänster , Höger } med Höger := − Vänster . Balansbrottet i fallet C == B repareras med en enkel rotation rotate_ (− C ), medan fallet C != B repareras med en dubbelrotation rotate_ CB .

Kostnaden för en rotation, antingen enkel eller dubbel, är konstant.

Enkel rotation

Figur 2 visar en Right Right-situation. I sin övre halva har nod X två barnträd med en balansfaktor på +2 . Dessutom är det inre barnet _t23 av Z (dvs vänster barn när Z är höger barn, eller höger barn när Z är vänster barn) inte högre än sitt syskon _t4 . Detta kan ske genom en höjdökning av underträdet t ₄ eller genom en höjdminskning av underträdet t ₁ . I det senare fallet kan även den bleka situationen där t ₂₃ har samma höjd som t ₄ förekomma.

Resultatet av vänsterrotationen visas i den nedre halvan av figuren. Tre länkar (tjocka kanter i figur 2) och två balansfaktorer ska uppdateras.

Som figuren visar låg bladskiktet före en insättning på nivå h+1, tillfälligt på nivå h+2 och efter rotationen igen på nivå h+1. Vid en deletion var bladskiktet på nivå h+2, där det återigen är, när t ₂₃ och t ₄ var av samma höjd. Annars når lövskiktet nivå h+1, så att höjden på det roterade trädet minskar.

Fig. 2: Enkel rotation rotate_Left ( X , Z )

Kodavsnitt för en enkel vänsterrotation

Inmatning:	X = roten till underträdet som ska roteras åt vänster
	Z = höger underordnad av X, Z är höger-tung
	med höjd == Höjd(VänsterSubträd( X ))+2
Resultat:	ny rot av ombalanserat underträd

     
    
       
      
       
          
      
      
    
    
       0  
             
             
     
     
          0
          0
    
      
 node  *  rotate_Left  (  nod  *  X  ,  node  *  Z  )  {  // Z är 2 högre än sitt syskon  t23  =  left_child  (  Z  );  // Inre underordnad av Z  höger_barn  (  X  )  =  t23  ;  if  (  t23  !=  null  )  förälder  (  t23  )  =  X  ;  left_child  (  Z  )  =  X  ;  förälder  (  X  )  =  Z  ;  // 1:a fallet, BF(Z) == 0,  // sker endast med radering, inte insättning:  om  (  BF  (  Z  )  ==  )  {  // t23 har varit av samma höjd som t4  BF  (  X  )  =  +  1  ;  // t23 nu högre  BF  (  Z  )  =  –  1  ;  // t4 nu lägre än X  }  annars  {  // Andra fallet händer med infogning eller radering:  BF  (  X  )  =  ;  BF  (  Z  )  =  ;  }  returnera  Z  ;  // returnera ny rot av roterat underträd  } 

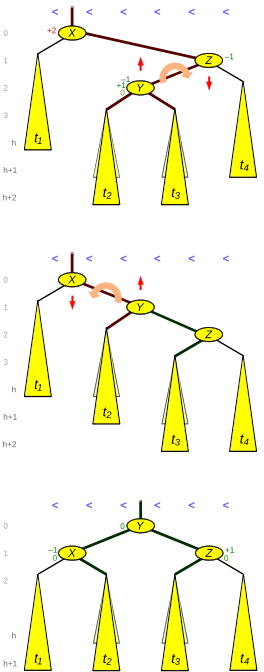
Dubbel rotation

Figur 3 visar en höger vänster-situation. I sin övre tredjedel har nod X två barnträd med en balansfaktor på +2 . Men till skillnad från figur 2 är det inre barnet Y till Z högre än sitt syskon t ₄ . Detta kan ske genom införandet av Y själv eller en höjdökning av ett av dess underträd t ₂ eller t ₃ (med konsekvensen att de har olika höjd) eller genom en höjdminskning av underträdet t ₁ . I det senare fallet kan det också förekomma att t ₂ och t ₃ är av samma höjd.

Resultatet av den första, den högra, rotationen visas i den mellersta tredjedelen av figuren. (Med avseende på balansfaktorerna är denna rotation inte av samma slag som de andra AVL enkelrotationerna, eftersom höjdskillnaden mellan Y och t 4 _bara är 1.) Resultatet av den sista vänsterrotationen visas i den nedre tredjedelen av figuren. Fem länkar (tjocka kanter i figur 3) och tre balansfaktorer ska uppdateras.

Som figuren visar låg bladskiktet före en insättning på nivå h+1, tillfälligt på nivå h+2 och efter dubbelrotationen igen på nivå h+1. Vid en deletion låg bladlagret på nivå h+2 och efter dubbelrotationen är det på nivå h+1, så att höjden på det roterade trädet minskar.

Fig. 3: Dubbelrotation rotate_RightLeft ( X , Z ) = rotate_Right runt Z följt av rotate_Left runt X

Kodavsnitt för dubbelrotation höger-vänster

Inmatning:	X = roten till underträdet som ska roteras
	Z = dess högra barn, vänstertungt
	med höjd == Höjd(VänsterSubträd( X ))+2
Resultat:	ny rot av ombalanserat underträd

     
    
       
    
      
      
       
          
      
      
      
      
       
          
      
      
    
    
       0 
          0
          0
     
    
           0  
                
              0
          
            
              0
                
        
      0
      
 node  *  rotate_RightLeft  (  nod  *  X  ,  node  *  Z  )  {  // Z är 2 högre än sitt syskon  Y  =  left_child  (  Z  );  // Inre barn till Z  // Y är 1 högre än syskon  t3  =  höger_barn  (  Y  );  vänster_barn  (  Z  )  =  t3  ;  if  (  t3  !=  null  )  förälder  (  t3  )  =  Z  ;  höger_barn  (  Y  )  =  Z  ;  förälder  (  Z  )  =  Y  ;  t2  =  vänster_barn  (  Y  );  höger_barn  (  X  )  =  t2  ;  if  (  t2  !=  null  )  förälder  (  t2  )  =  X  ;  vänster_barn  (  Y  )  =  X  ;  förälder  (  X  )  =  Y  ;  // 1:a fallet, BF(Y) == 0,  // sker endast med radering, inte insättning:  if  (  BF  (  Y  )  ==  )  {  BF  (  X  )  =  ;  BF  (  Z  )  =  ;  }  annars  // andra fall händer med infogning eller radering:  if  (  BF  (  Y  )  >  )  {  // t3 var högre  BF  (  X  )  =  –  1  ;  // t1 nu högre  BF  (  Z  )  =  ;  }  else  {  // t2 var högre  BF  (  X  )  =  ;  BF  (  Z  )  =  +1  ;  _  // t4 nu högre  }  BF  (  Y  )  =  ;  returnera  Y  ;  // returnera ny rot av roterat underträd  } 

Jämförelse med andra strukturer

Både AVL-träd och röd-svarta (RB) träd är självbalanserande binära sökträd och de är matematiskt relaterade. Visserligen kan varje AVL-träd färgas röd–svart, men det finns RB-träd som inte är AVL-balanserade. För att bibehålla AVL (eller RB-trädets invarianter) spelar rotationer en viktig roll. I värsta fall, även utan rotationer, kräver AVL- eller RB-insättningar eller -raderingar O(log n ) -inspektioner och/eller uppdateringar av AVL-balansfaktorer (eller RB-färger). RB-insättningar och -deletioner och AVL-insättningar kräver från noll till tre svansrekursiva rotationer och körs i amorterad O(1) -tid, alltså lika konstant i genomsnitt. AVL-deletioner som kräver O(log n ) -rotationer i värsta fall är också O(1) i genomsnitt. RB-träd kräver att man lagrar en bit information (färgen) i varje nod, medan AVL-träd oftast använder två bitar för balansfaktorn, även om det räcker med en bit med betydelsen "lägre än syskon" när de lagras hos barnen. Den större skillnaden mellan de två datastrukturerna är deras höjdgräns.

För ett träd av storlek n ≥ 1

• ett AVL-träds höjd är högst

  ${\displaystyle {\begin{array}{ll}h&\leqq \;c \log _{2}(n+d)+b\\&<\;c\log _{2}(n+2)+b\end{array}}} där$

  φ $\varphi :={\tfrac {1+{\sqrt {5}}}{2}}\approx 1.618$ det gyllene snittet , $c:= {\tfrac {1}{\log _{2}\varphi }}\approx 1.440,$$b:={\tfrac {c}{ 2}}\log _{2}5-2\approx \;-0.328,$ och $d:=1+{\tfrac {1}{\varphi ^ {4}{\sqrt {5}}}}\approx 1,065$ .

• ett RB-träds höjd är högst

  ${\begin{array}{ll}h&\leqq \;2\log _{2}(n+1)\end{ array}}$ .

AVL-träd är mer styvt balanserade än RB-träd med en asymptotisk relation AVL/RB ≈0,720 av de maximala höjderna. För insättningar och deletioner visar Ben Pfaff i 79 mätningar en relation mellan AVL/RB mellan 0,677 och 1,077 med median ≈0,947 och geometriskt medelvärde ≈0,910.

Se även

• WAVL-träd
• Splay träd
• Syndbock träd
• B-träd
• T-träd
• Lista över datastrukturer

Vidare läsning

•   Donald Knuth . The Art of Computer Programming , Volym 3: Sortering och sökning , tredje upplagan. Addison-Wesley, 1997. ISBN 0-201-89685-0 . Sidorna 458–475 i avsnitt 6.2.3: Balanserade träd.
•    Haeupler, Bernhard; Sen, Siddhartha; Tarjan, Robert E. (2015), "Rank-balanced trees" (PDF) , ACM Transactions on Algorithms , 11 (4): Art. 30, 26, doi : 10.1145/2689412 , MR 3361215 , S2CID 1407290 .

externa länkar

• Den här artikeln innehåller material som är allmän egendom från Paul E. Black. "AVL-träd" . Ordbok över algoritmer och datastrukturer . NIST .