Röd-svart träd
| Röd-svart träd | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Typ | Träd | ||||||||||||||||||||||||||||
| Uppfunnet | 1972 | ||||||||||||||||||||||||||||
| Uppfunnet av | Rudolf Bayer | ||||||||||||||||||||||||||||
| Komplexiteter i stor O-notation | |||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
Inom datavetenskap är ett rött-svart träd en specialiserad binär sökträdsdatastruktur noterad för snabb lagring och hämtning av beställd information, och en garanti för att operationerna kommer att slutföras inom en känd tid . Jämfört med andra självbalanserande binära sökträd håller noderna i ett röd-svart träd en extra bit som kallas "färg" som representerar "röd" och "svart" som används vid omorganisering av trädet för att säkerställa att det alltid är ungefär balanserad.
När trädet modifieras, arrangeras det nya trädet om och "målas om" för att återställa färgegenskaperna som begränsar hur obalanserat trädet i värsta fall kan bli. Egenskaperna är utformade så att denna omarrangering och omfärgning kan utföras effektivt.
(Om)balanseringen är inte perfekt, men garanterar sökning i tid, där är antalet poster (eller nycklar) i träd. Åtgärderna för att infoga och ta bort, tillsammans med omarrangering av träd och omfärgning, utförs också i tid.
Att spåra färgen på varje nod kräver bara en bit information per nod eftersom det bara finns två färger. Trädet innehåller ingen annan data som är specifik för att det är ett röd-svart träd, så dess minnesavtryck är nästan identiskt med det för ett klassiskt (ofärgat) binärt sökträd . I vissa fall kan den tillagda informationsbiten lagras utan extra minneskostnad.
Historia
År 1972 uppfann Rudolf Bayer en datastruktur som var en speciell order-4-fall av ett B-träd . Dessa träd upprätthöll alla vägar från rot till löv med samma antal noder, vilket skapade perfekt balanserade träd. De var dock inte binära sökträd. Bayer kallade dem ett "symmetriskt binärt B-träd" i sin tidning och senare blev de populära som 2–3–4 träd eller bara 2–4 träd.
I en artikel från 1978, "A Dichromatic Framework for Balanced Trees", härledde Leonidas J. Guibas och Robert Sedgewick det röd-svarta trädet från det symmetriska binära B-trädet. Färgen "röd" valdes eftersom det var den snyggaste färgen som producerades av färglaserskrivaren som var tillgänglig för författarna när de arbetade på Xerox PARC . Ett annat svar från Guibas säger att det var på grund av de röda och svarta pennorna som de hade tillgång till för att rita träden.
1993 introducerade Arne Andersson idén om ett högerlutat träd för att förenkla insättnings- och raderingsoperationer.
1999 visade Chris Okasaki hur man gör skäroperationen rent funktionell. Dess balansfunktion behövde endast ta hand om 4 obalanserade fall och ett standardbalanserat fall.
Den ursprungliga algoritmen använde 8 obalanserade fall, men Cormen et al. (2001) reducerade det till 6 obalanserade fall. Sedgewick visade att infogningsoperationen kan implementeras i bara 46 rader Java -kod. 2008 föreslog Sedgewick det vänsterlutade röd-svarta trädet, och utnyttjade Anderssons idé som förenklade insättnings- och raderingsoperationerna. Sedgewick tillät ursprungligen noder vars två barn är röda, vilket gjorde hans träd mer som 2–3–4 träd, men senare lades denna begränsning till, vilket gjorde nya träd mer som 2–3 träd. Sedgewick implementerade infogningsalgoritmen på bara 33 rader, vilket avsevärt förkortade hans ursprungliga 46 rader kod.
Terminologi
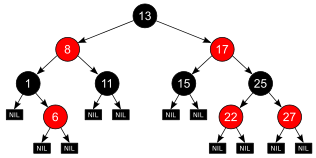
Ett rött-svart träd är en speciell typ av binärt sökträd , som används inom datavetenskap för att organisera delar av jämförbara data , såsom textfragment eller siffror (som t.ex. siffrorna i figurerna 1 och 2). Noderna som bär nycklar och/eller data kallas ofta "interna noder" , men för att göra detta mycket specifikt kallas de även icke-NIL-noder i den här artikeln.
Bladnoderna hos rödsvarta träd ( NIL i figur 1) innehåller inga nycklar eller data . Dessa "blad" behöver inte vara explicita individer i datorns minne: en NULL-pekare kan — som i alla binära träddatastrukturer — koda det faktum att det inte finns någon underordnad nod på denna position i (förälder)noden. Ändå, genom sin position i trädet, är dessa objekt i relation till andra noder som är relevanta för RB-strukturen, det kan ha förälder, syskon (dvs. det andra barnet till föräldern), farbror, till och med brorsonnod; och kan vara barn – men aldrig förälder till en annan nod. Det är egentligen inte nödvändigt att tillskriva en "färg" till dessa end-of-path-objekt, eftersom villkoret "är NIL eller SVART " antyds av villkoret "är NIL " (se även denna anmärkning ).
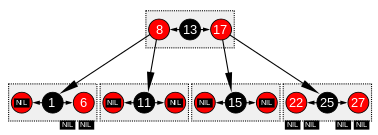
Figur 2 visar konceptuellt samma röd-svarta träd utan dessa NIL-löv. För att komma fram till samma begrepp om en väg måste man lägga märke till att t.ex. 3 vägar går genom noden 1 , nämligen en väg genom 1 vänster plus 2 tillagda vägar genom 1 höger , nämligen vägarna genom 6 vänster och 6 höger . På så sätt är dessa ändar av banorna också dockningspunkter för nya noder som ska infogas, helt ekvivalent med NIL-bladen i figur 1.
Istället, för att spara en marginell mängd exekveringstid, kan dessa (möjligen många) NIL-blad implementeras som pekare till en unik (och svart) sentinelnod (istället för pekare med värdet NULL ).
Som en slutsats kan det faktum att ett barn inte existerar (inte är en sann nod, inte innehåller data) i alla fall specificeras av samma NULL-pekare eller som samma pekare till en sentinel-nod. I den här artikeln kallas båda valen NIL-nod och har det konstanta värdet NIL .
Det svarta djupet för en nod definieras som antalet svarta noder från roten till den noden (dvs antalet svarta förfäder). Den svarta höjden på ett rött-svart träd är antalet svarta noder i varje bana från roten till bladen, som, enligt krav 4 , är konstant (alternativt kan det definieras som det svarta djupet för vilken lövnod som helst). Den svarta höjden på en nod är den svarta höjden på underträdet som är rotat av den. I den här artikeln ska den svarta höjden för en NIL-nod sättas till 0, eftersom dess underträd är tomt enligt figur 2, och dess trädhöjd är också 0.
Egenskaper
Utöver de krav som ställs på ett binärt sökträd måste följande uppfyllas av ett rött-svart träd:
- Varje nod är antingen röd eller svart.
- Alla NIL-noder (figur 1) anses vara svarta.
- En röd nod har inte ett rött barn.
- Varje väg från en given nod till någon av dess underliggande NIL-noder går genom samma antal svarta noder.
Vissa författare, t.ex. Cormen et al., hävdar att "roten är svart" som femte krav; men inte Mehlhorn & Sanders eller Sedgewick & Wayne. Eftersom roten alltid kan ändras från röd till svart har denna regel liten effekt på analysen. Den här artikeln utelämnar det också, eftersom det lite stör de rekursiva algoritmerna och bevisen.
Som ett exempel är varje perfekt binärt träd som endast består av svarta noder ett rött-svart träd.
De skrivskyddade operationerna, såsom sökning eller trädpassering, påverkar inte något av kraven. Däremot upprätthåller modifieringsoperationerna att infoga och ta bort enkelt krav 1 och 2, men med avseende på de andra kraven måste en viss extra ansträngning göras för att undvika att införa en överträdelse av krav 3, kallad röd överträdelse, eller av krav 4, kallas en svart-kränkning .
Kraven upprätthåller en kritisk egenskap hos rödsvarta träd: vägen från roten till det längsta bladet är inte mer än dubbelt så lång som vägen från roten till närmaste blad . Resultatet är att trädet är höjdbalanserat . Eftersom operationer som att infoga, ta bort och hitta värden kräver värsta tänkbara tid proportionell mot trädets höjd logaritmisk i antalet av poster, dvs , vilket inte är fallet för vanliga binära sökträd . För ett matematiskt bevis se avsnittet Bevis för gränser .
Röd-svarta träd, precis som alla binära sökträd , tillåter ganska effektiv sekventiell åtkomst (t.ex. in-order traversal , det vill säga: i ordningen Vänster–Root–Höger) av deras element. Men de stöder också asymptotiskt optimal direktåtkomst via en genomgång från rot till blad, vilket resulterar i söktid.
Analogi med B-träd av ordning 4
Ett röd-svart träd liknar strukturen ett B-träd av ordning 4, där varje nod kan innehålla mellan 1 och 3 värden och (i enlighet därmed) mellan 2 och 4 underordnade pekare. I ett sådant B-träd kommer varje nod endast att innehålla ett värde som matchar värdet i en svart nod i det röd-svarta trädet, med ett valfritt värde före och/eller efter det i samma nod, båda matchar en ekvivalent röd nod på det rödsvarta trädet.
Ett sätt att se denna ekvivalens är att "flytta upp" de röda noderna i en grafisk representation av det röd-svarta trädet, så att de hamnar horisontellt med sin överordnade svarta nod, genom att tillsammans skapa ett horisontellt kluster. I B-trädet, eller i den modifierade grafiska representationen av det röd-svarta trädet, är alla bladnoder på samma djup.
Det rödsvarta trädet motsvarar då strukturellt ett B-träd av ordning 4, med en minsta fyllningsfaktor på 33 % av värdena per kluster med en maximal kapacitet på 3 värden.
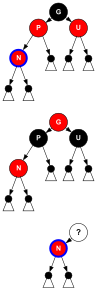
Denna B-trädstyp är dock fortfarande mer allmän än ett rött-svart träd, eftersom det tillåter tvetydighet i en röd-svart trädkonvertering - flera röd-svarta träd kan produceras från ett ekvivalent B-träd av ordning 4 (se figur 3) ). Om ett B-trädkluster bara innehåller 1 värde, är det minimum, svart och har två underordnade pekare. Om ett kluster innehåller 3 värden kommer det centrala värdet att vara svart och varje värde som lagras på dess sidor kommer att vara rött. Om klustret innehåller två värden kan dock endera bli den svarta noden i det röd-svarta trädet (och den andra blir röd).
Så ordning-4 B-trädet upprätthåller inte vilket av värdena som finns i varje kluster som är det svarta rotträdet för hela klustret och föräldern till de andra värdena i samma kluster. Trots detta är operationerna på rödsvarta träd mer tidsekonomiska eftersom man inte behöver behålla värdevektorn. Det kan bli kostsamt om värden lagras direkt i varje nod istället för att lagras genom referens. B-trädnoder är dock mer ekonomiska i utrymmet eftersom du inte behöver lagra färgattributet för varje nod. Istället måste du veta vilken lucka i klustervektorn som används. Om värden lagras genom referens, t.ex. objekt, kan nollreferenser användas och så kan klustret representeras av en vektor som innehåller 3 luckor för värdepekare plus 4 luckor för underordnade referenser i trädet. I så fall kan B-trädet vara mer kompakt i minnet, vilket förbättrar datalokaliteten.
Samma analogi kan göras med B-träd med större beställningar som strukturellt kan motsvara ett färgat binärt träd: du behöver bara fler färger. Anta att du lägger till blått, då det blå–röda–svarta trädet definieras som röd–svarta träd men med den ytterligare begränsningen att inga två på varandra följande noder i hierarkin kommer att vara blå och alla blå noder kommer att vara barn till en röd nod, då blir ekvivalent med ett B-träd vars kluster kommer att ha högst 7 värden i följande färger: blå, röd, blå, svart, blå, röd, blå (För varje kluster kommer det att finnas högst 1 svart nod, 2 röda noder och 4 blå noder).
För måttliga volymer av värden är infogning och radering i ett färgat binärt träd snabbare jämfört med B-träd eftersom färgade träd inte försöker maximera fyllningsfaktorn för varje horisontellt kluster av noder (endast den minsta fyllningsfaktorn garanteras i färgad binär träd, vilket begränsar antalet delar eller korsningar av kluster). B-träd kommer att vara snabbare för att utföra rotationer (eftersom rotationer ofta förekommer inom samma kluster snarare än med flera separata noder i ett färgat binärt träd). För lagring av stora volymer blir dock B-träd mycket snabbare då de blir mer kompakta genom att gruppera flera barn i samma kluster där de kan nås lokalt.
Alla möjliga optimeringar i B-träd för att öka de genomsnittliga fyllningsfaktorerna för kluster är möjliga i det ekvivalenta flerfärgade binära trädet. Noterbart är att maximera den genomsnittliga fyllningsfaktorn i ett strukturellt ekvivalent B-träd är detsamma som att minska den totala höjden på det flerfärgade trädet, genom att öka antalet icke-svarta noder. Det värsta fallet inträffar när alla noder i ett färgat binärt träd är svarta, det bästa fallet inträffar när endast en tredjedel av dem är svarta (och de andra två tredjedelarna är röda noder).
Rödsvarta träd erbjuder värsta tänkbara garantier för insättningstid, raderingstid och söktid. Detta gör dem inte bara värdefulla i tidskänsliga applikationer som realtidsapplikationer , utan det gör dem till värdefulla byggstenar i andra datastrukturer som ger värsta tänkbara garantier; till exempel kan många datastrukturer som används i beräkningsgeometri baseras på röd-svarta träd, och Completely Fair Scheduler som används i nuvarande Linux- kärnor och implementering av epoll -systemanrop använder röd-svarta träd.
AVL -trädet är en annan struktur som stöder sökning, infogning och borttagning. AVL-träd kan färgas röd-svart, och är alltså en undergrupp av RB-träd. Värsta tänkbara höjden är 0,720 gånger den värsta höjden för RB-träd, så AVL-träden är mer styvt balanserade. Prestandamätningarna av Ben Pfaff med realistiska testfall i 79 körningar finner AVL till RB-förhållanden mellan 0,677 och 1,077, median vid 0,947 och geometriskt medelvärde 0,910. WAVL-träd har en prestanda mellan dessa två.
Röd-svarta träd är också särskilt värdefulla i funktionell programmering , där de är en av de vanligaste beständiga datastrukturerna , som används för att konstruera associativa arrayer och uppsättningar som kan behålla tidigare versioner efter mutationer. Den beständiga versionen av röd-svarta träd kräver utrymme för varje infogning eller borttagning, förutom tid.
För varje 2–4 träd finns det motsvarande röd-svarta träd med dataelement i samma ordning. Insättnings- och raderingsoperationerna på 2–4 träd motsvarar också färgvändning och rotationer i röd-svarta träd. Detta gör 2–4 träd till ett viktigt verktyg för att förstå logiken bakom rödsvarta träd, och det är därför som många inledande algoritmtexter introducerar 2–4 träd precis före rödsvarta träd, även om 2–4 träd inte ofta används i öva.
2008 introducerade Sedgewick en enklare version av det röd-svarta trädet som kallas det vänsterlutade röd-svarta trädet genom att eliminera en tidigare ospecificerad frihetsgrad i implementeringen. LLRB upprätthåller en extra invariant att alla röda länkar måste luta åt vänster förutom under infogning och borttagning. Rödsvarta träd kan göras isometriska till antingen 2–3 träd eller 2–4 träd, för valfri sekvens av operationer. 2–4-trädets isometri beskrevs 1978 av Sedgewick. Med 2–4 träd löses isometrin av en "färgvändning", motsvarande en splittring, där den röda färgen på två barnnoder lämnar barnen och flyttar till föräldernoden.
Den ursprungliga beskrivningen av tangoträdet , en typ av träd optimerad för snabba sökningar, använder specifikt rödsvarta träd som en del av sin datastruktur.
Från och med Java 8 har HashMap modifierats så att istället för att använda en LinkedList för att lagra olika element med kolliderande hashkoder , används ett röd-svart träd. Detta resulterar i en förbättring av tidskomplexiteten för att söka efter ett sådant element från till där är antalet element med kolliderande hashkoder.
Operationer
De skrivskyddade operationerna, såsom sökning eller trädpassering, på ett röd-svart träd kräver ingen modifiering från de som används för binära sökträd , eftersom varje röd-svart träd är ett specialfall av ett enkelt binärt sökträd. Det omedelbara resultatet av en insättning eller borttagning kan dock bryta mot egenskaperna hos ett röd-svart träd, vars återställande kallas rebalansering så att röd-svarta träd blir självbalanserande. Det kräver i värsta fall ett litet antal, i Big O notation , där är antalet objekt i trädet, i genomsnitt resp. amorterad ett konstant antal färgförändringar (vilka är mycket snabba i praktiken); och inte mer än tre trädrotationer (två för insättning).
Om exempelimplementeringen nedan inte är lämplig kan andra implementeringar med förklaringar finnas i Ben Pfaffs kommenterade C-bibliotek GNU libavl (v2.0.3 från och med juni 2019).
Detaljerna för insättnings- och borttagningsoperationerna kommer att demonstreras med exempel på C++- kod, som använder typdefinitionerna, makron nedan och hjälpfunktionen för rotationer:
// Grundläggande typdefinitioner: enum color_t { SVART , RÖD }; struct RBnode { // nod för röd–svart träd RBnode * parent ; // == NIL om roten av trädet RBnode * barn [ 2 ]; // == NIL om barnet är tomt // Indexet är: // VÄNSTER := 0, if (nyckel < parent->key) // RIGHT := 1, if (nyckel > parent->key) enum color_t color ; int nyckel ; }; #define NIL NULL // nollpekare eller pekare till sentinel nod #define LEFT 0 #define RIGHT 1 #define left child[LEFT] #define right child[RIGHT] struct RBtree { // red–black tree RBnode * root ; // == NIL om trädet är tomt }; // Hämta den underordnade riktningen (∈ { VÄNSTER, HÖGER }) // för icke-roten icke-NIL RBnod* N: #define childDir(N) ( N == (N->parent)->right ? HÖGER : VÄNSTER )
RBnode * RotateDirRoot ( RBtree * T , // röd–svart träd RBnode * P , // roten av underträdet ( kan vara roten till T ) int dir ) { // dir ∈ { VÄNSTER, HÖGER } RBnod * G = P - > förälder ; RBnod * S = P -> barn [ 1 - dir ]; RBnod * C ; hävda ( S != NIL ); // pekare till sann nod krävs C = S -> barn [ dir ]; P -> barn [ 1 - dir ] = C ; om ( C != NIL ) C- > förälder = P ; S -> barn [ dir ] = P ; P -> förälder = S ; S -> förälder = G ; om ( G != NULL ) G -> barn [ P == G -> eller hur ? HÖGER : VÄNSTER ] = S ; annars T -> rot = S ; returnera S ; // ny rot av underträd } #define RotateDir(N,dir) RotateDirRoot(T,N,dir) #define RotateLeft(N) RotateDirRoot(T,N,LEFT) #define RotateRight(N) RotateDirRoot(T,N,RIGHT) )
Anmärkningar till exempelkoden och diagram för insättning och borttagning
Förslaget delar upp både insättning och borttagning (för att inte nämna några mycket enkla fall), i sex konstellationer av noder, kanter och färger, som kallas fall. Förslaget innehåller för båda, insättning och borttagning, exakt ett fall som flyttar fram en svart nivå närmare roten och slingorna, de andra fem fallen balanserar om sitt eget träd. De mer komplicerade fallen visas i ett diagram.
- Variabeln
Nbetecknar den aktuella noden, som är märkt med N i diagrammen. -


 symboliserar en röd nod och en (icke-NIL) svart nod (med svart höjd ≥ 1), symboliserar färgen röd eller svart för en icke-NIL-nod, men samma färg genom hela samma diagram. NIL-noder är inte representerade i diagrammen.
symboliserar en röd nod och en (icke-NIL) svart nod (med svart höjd ≥ 1), symboliserar färgen röd eller svart för en icke-NIL-nod, men samma färg genom hela samma diagram. NIL-noder är inte representerade i diagrammen. - Ett diagram innehåller tre kolumner och två till fyra åtgärder. Den vänstra kolumnen visar den första iterationen, den högra kolumnen de högre iterationerna, den mellersta kolumnen visar segmenteringen av ett fall i dess olika åtgärder.
-
Åtgärden "entry" visar konstellationen av noder med deras färger som definierar ett fall och oftast bryter mot några av kraven . En blå kant ringer den nuvarande noden N och de andra noderna är märkta enligt deras relation till N . - Om en rotation anses användbar, visas detta i nästa åtgärd, som är märkt "rotation".
- Om någon omfärgning anses användbar, visas detta i nästa åtgärd, som är märkt "färg".
-
Om det fortfarande finns ett visst behov av att reparera, använder fallen kod för andra fall och detta efter en omtilldelning av den aktuella noden N , som sedan återigen bär en blå ring och i förhållande till vilken andra noder också kan behöva omtilldelas. Denna åtgärd är märkt "tilldela om". För båda, infoga och ta bort, finns det (exakt) ett fall som itererar en svart nivå närmare roten; då uppfyller den omtilldelade konstellationen respektive slinginvariant.
-

 En möjligen numrerad triangel med en svart cirkel ovanpå representerar ett rött–svart underträd (anslutet till dess förälder enligt krav 3 ) med en svart höjd lika med iterationsnivån minus ett, dvs noll i den första iterationen. Dess rot kan vara röd eller svart. En möjligen numrerad triangel representerar ett rött-svart underträd med en svart höjd en mindre, dvs dess förälder har svart höjd noll i den andra iterationen.
En möjligen numrerad triangel med en svart cirkel ovanpå representerar ett rött–svart underträd (anslutet till dess förälder enligt krav 3 ) med en svart höjd lika med iterationsnivån minus ett, dvs noll i den första iterationen. Dess rot kan vara röd eller svart. En möjligen numrerad triangel representerar ett rött-svart underträd med en svart höjd en mindre, dvs dess förälder har svart höjd noll i den andra iterationen.
- Anmärkning
- För enkelhetens skull använder exempelkoden disjunktionen : U
== NIL || U->färg == SVART // anses vara svart
- och konjunktionen :
U != NIL && U->färg == RÖD // anses inte vara svart
-
. Därmed måste man hålla i minnet att båda påståendena inte utvärderas totalt, omU == NIL. Då berörs inteU->färgi båda fallen (se Kortslutningsutvärdering ). (Kommentarensom betraktas som svartöverensstämmer med krav 2 .) - De relaterade
if-påståendena måste förekomma mycket mer sällan om förslaget förverkligas.
Införande
Insättningen börjar med att den nya (icke-NIL) noden, säg N , placeras i positionen i det binära sökträdet för en NIL-nod vars föregångare i sin ordning jämförs med mindre än den nya nodens nyckel, som i sin tur jämför mindre än nyckeln. av dess efterträdare i ordning. (Ofta är denna positionering resultatet av en sökning i trädet omedelbart före infogningsoperationen och består av en nod P tillsammans med en riktning dir med P->child[dir] == NIL .) Den nyligen infogade noden är tillfälligt färgad röd så att alla banor innehåller samma antal svarta noder som tidigare. Men om dess förälder, säg P , också är röd så introducerar denna åtgärd en röd överträdelse .
void RBinsert1 ( RBtree * T , // -> röd–svart trädstruktur RBnode * N , // - > nod som ska infogas struct RBnode * P , // -> föräldernod till N ( kan vara NULL ) byte dir ) / / sida ( VÄNSTER eller HÖGER ) om P där man ska infoga N { struct RBnode * G ; // -> föräldernod för P struct RBnode * U ; // -> farbror till N N -> färg = RÖD ; N -> vänster = NIL ; N -> höger = NIL ; N -> förälder = P ; if ( P == NULL ) { // Det finns inget överordnat T -> rot = N ; // N är den nya roten av trädet T. return ; // infogning klar } P -> barn [ dir ] = N ; // infoga N som dir-child av P // början av (do while)-loopen: do {
Ombalanseringsslingan för infogningsoperationen har följande invariant :
-
 Den aktuella noden N är (röd) i början av varje iteration.
Den aktuella noden N är (röd) i början av varje iteration. - Krav 3 är uppfyllt för alla par node←förälder med det möjliga undantaget N ← P när P också är rött (en röd överträdelse vid N ).
- Alla andra egenskaper (inklusive krav 4 ) är uppfyllda i hela trädet.
Anmärkningar till infogningsdiagrammen
| innan |
fall → |
rotation _ |
uppdrag _ |
efter |
→ nästa |
Δh | ||||||
| P | G | U | x | P | G | U | x | |||||
| — | I3 | → | ||||||||||
| I1 | → | |||||||||||
| — | I4 | → | ||||||||||
| I2 | N := G | ? | ? | 2 | ||||||||
| i | I5 | P ↶ N | N := P | o | I6 | 0 | ||||||
| o | I6 | P ↷ G | → | |||||||||
|
Infogning: Denna synopsis visar i dess före- kolumner att alla möjliga fall av konstellationer täcks. |
||||||||||||
- I diagrammen används P för N :s förälder, G för farföräldern, och U kommer att beteckna N :s farbror.
- Diagrammen visar föräldranoden P som det vänstra barnet till dess förälder G även om det är möjligt för P att vara på vardera sidan. Exempelkoden täcker båda möjligheterna med hjälp av sidovariabeln
dir. - N är insättningsnoden, men allteftersom operationen fortskrider kan även andra noder bli aktuella (se fall I2 ).
- Diagrammen visar de fall där P är rött också, den röda överträdelsen.
- Kolumnen x indikerar förändringen i barnriktningen, dvs o (för "yttre") betyder att P och N båda är vänster eller båda höger barn, medan i (för "inre") betyder att barnriktningen ändras från P till N :s.
- Kolumngruppen före definierar fallet, vars namn anges i kolumnen fallet . Därmed ignoreras möjliga värden i celler som lämnas tomma. Så i fall I2 täcker provkoden båda möjligheterna för barnriktningar för N , även om motsvarande diagram endast visar en.
- Raderna i synopsis är ordnade så att täckningen av alla möjliga RB-fall är lätt att förstå.
- Kolumnrotationen anger om en rotation bidrar till ombalanseringen .
- Kolumntilldelningen visar en tilldelning av N innan du går in i ett efterföljande steg. Detta inducerar möjligen en omtilldelning av de andra noderna P , G , U också.
- Om något har ändrats av ärendet visas detta i kolumngruppen efter .
- En pil → i kolumnen härnäst betyder att ombalanseringen är klar med detta steg. Om kolumnen efter bestämmer exakt ett fall, anges detta fall som det efterföljande, annars finns det frågetecken.
- Slingan finns i avsnitten "Infoga fall I1" och "Infoga fall I2" , där i fall I2 problemet med ombalansering eskaleras trädnivåer eller 1 svartnivå högre i trädet, genom att farfadern G blir den nya nuvarande noden N . Så det tar maximalt iterationssteg för att reparera trädet (där är trädets höjd). Eftersom sannolikheten för eskalering minskar exponentiellt för varje steg är den totala ombalanseringskostnaden konstant i genomsnitt, faktiskt avskriven konstant .
- Från slingans kropp går fall I1 ut av sig självt och det finns utgående grenar till fall I4 , I6 , I5 + I6 och I3 .
- Rotationer sker i fall I6 och I5 + I6 – utanför slingan. Därför förekommer högst två rotationer totalt.
Sätt i fodral I1
Den nuvarande nodens överordnade P är svart, så krav 3 gäller. Krav 4 gäller även enligt loopinvarianten .
if ( P -> färg == SVART ) { // Fall_I1 (P svart): return ; // insättningen klar } // Från och med nu är P rött. if (( G = P -> parent ) == NULL ) goto Case_I4 ; // P röd och rot // annat: P röd och G!=NULL. dir = barnDir ( P ); // sidan av förälder G på vilken nod P är placerad U = G -> barn [ 1 - dir ]; // farbror om ( U == NIL || U -> färg == SVART ) // anses svart goto Case_I56 ; // P röd && U svart
Sätt i fodral I2
Om både föräldern P och farbror U är röda kan båda målas om svarta och morföräldern G blir röd för att upprätthålla krav 4 . Eftersom varje väg genom föräldern eller farbrorn måste passera genom farföräldern, har antalet svarta noder på dessa vägar inte ändrats. Farföräldern G kan dock nu bryta mot krav 3, om den har en röd förälder. Efter ommärkning av G till N är slinginvarianten uppfylld så att ombalanseringen kan itereras på en svart nivå (= 2 trädnivåer) högre .
// Fall_I2 (P+U röd): P -> färg = SVART ; U -> färg = SVART ; G -> färg = RÖD ; N = G ; // ny nuvarande nod // iterera 1 svart nivå högre // (= 2 trädnivåer) } while (( P = N -> parent ) != NULL ); // slutet av (do while)-loopen
Sätt i fodral I3
Infoga fall I2 har utförts i gånger och trädets totala höjd har ökat med 1, nu är Den aktuella noden N är trädets (röda) rot, och alla RB-egenskaper är uppfyllda.
// Lämnar (do while)-loopen (efter att ha fallit igenom från Case_I2). // Case_I3: N är roten och röd. återvända ; // infogning klar
Sätt i fodral I4
Föräldern P är röd och roten. Eftersom N också är rött överträds krav 3. Men efter att ha bytt P :s färg är trädet i RB-form. Den svarta höjden på trädet ökar med 1.
Case_I4 : // P är roten och röd: P -> färg = SVART ; återvända ; // infogning klar
Sätt i fodral I5
Föräldern P är röd men farbror U är svart. Det slutliga målet är att rotera föräldranoden P till farförälderns position, men detta kommer inte att fungera om N är ett "inre" barnbarn till G (dvs. om N är det vänstra barnet till det högra barnet till G eller det högra barnet till G det vänstra barnet till G ). En dir -rotation vid P växlar rollerna för den nuvarande noden N och dess förälder P. Rotationen lägger till banor genom N (de i underträdet märkta 2 , se diagram) och tar bort banor genom P (de i underträdet märkta 4 ). Men både P och N är röda, så krav 4 bevaras. Krav 3 återställs i fall 6.
Case_I56 : // P röd && U svart: if ( N == P -> barn [ 1 - dir ]) { // Case_I5 (P röd && U svart && N inre barnbarn till G): RotateDir ( P , dir ); // P är aldrig roten N = P ; // ny aktuell nod P = G -> barn [ dir ]; // ny förälder till N // faller igenom till Case_I6 }
Sätt i fodral I6
Den nuvarande noden N är nu säker på att vara ett "yttre" barnbarn till G (vänster om vänster barn eller höger om höger barn). Nu (1-dir) -rotera vid G , sätt P i stället för G och gör P till förälder till N och G . G är svart och dess tidigare barn P är rött, eftersom krav 3 överträddes. Efter att ha bytt färgerna på P och G uppfyller det resulterande trädet krav 3. Krav 4 förblir också uppfyllt, eftersom alla vägar som gick genom det svarta G nu går genom det svarta P .
// Case_I6 (P röd && U svart && N yttre barnbarn till G): RotateDirRoot ( T , G , 1 - dir ); // G kan vara roten P -> färg = SVART ; G -> färg = RÖD ; återvända ; // insättningen klar } // slutet av RBinsert1
Eftersom algoritmen omvandlar indata utan att använda en extra datastruktur och endast använder en liten mängd extra lagringsutrymme för hjälpvariabler är den på plats .
Borttagning
Enkla fall
Etiketten N betecknar den aktuella noden som vid ingången är den nod som ska raderas.
Om N är roten som inte har ett icke-NIL-barn, ersätts den av en NIL-nod, varefter trädet är tomt — och i RB-form.
Om N har exakt ett icke-NIL-barn måste det vara ett rött barn, för om det vore ett svart skulle krav 4 tvinga fram ett andra svart icke-NIL-barn.
Om N är en röd nod kan den inte ha exakt ett icke-NIL-barn, eftersom detta måste vara svart enligt krav 3 . Dessutom kan den inte ha exakt ett svart barn som argumenterats ovan. Som en konsekvens är den röda noden N utan något barn och kan helt enkelt tas bort.
Om N är en svart nod kan den ha ett rött barn eller inget icke-NIL-barn alls. Om N har ett rött barn byts det helt enkelt ut mot detta barn efter att ha målat det senare svart.
Om N har två icke-NIL-barn, hittar en ytterligare navigering till minimielementet i dess högra underträd (som är N :s efterföljare i ordning, säg en nod med nej annan nod mellan N och (som visas här ). Denna nod har inte ett vänsterbarn och har därför högst ett icke-NIL-barn. Om ska tas bort i stället för N , kommer de röd-svarta träddata relaterade till N och , dvs färgen på och pekarna till och från de två noderna måste bytas ut. (Som ett resultat är det modifierade röd-svarta trädet detsamma som tidigare, förutom att ordningen mellan N och är omvänd.) Detta val kan resultera i ett av de enklare fall ovan, men om är utan barn och svart kommer vi fram till ...
Borttagning av ett svart icke-rotblad
Det komplexa fallet är när N inte är roten, färgad svart och inte har något eget barn (⇔ endast NIL-barn). I den första iterationen ersätts N med NIL.
void RBdelete2 ( RBtree * T , // -> röd–svart trädstruktur RBnode * N ) // -> nod som ska raderas { struct RBnode * P = N -> parent ; // -> överordnad nod för N byte dir ; // sidan av P på vilken N är placerad (∈ { VÄNSTER, HÖGER }) struct RBnode * S ; // -> syskon till N struct RBnode * C ; // -> stäng brorson struktur RBnode * D ; // -> avlägsen brorson // P != NULL, eftersom N inte är roten. dir = barnDir ( N ); // sidan av förälder P där noden N är belägen // Ersätt N vid dess förälder P med NIL: P -> barn [ dir ] = NIL ; gå till Start_D ; // hoppa in i loopen // början av (do while)-loopen: do { dir = childDir ( N ); // sidan av förälder P på vilken nod N finns Start_D : S = P -> barn [ 1 - dir ]; // syskon till N (har svart längd >= 1) D = S -> barn [ 1 - dir ]; // avlägsen brorson C = S -> barn [ dir ]; // nära brorson om ( S -> färg == RÖD ) goto Case_D3 ; // S röd ===> P+C+D svart // S är svart: om ( D != NIL && D -> färg == RÖD ) // anses inte vara svart goto Case_D6 ; // D röd && S svart om ( C != NIL && C -> färg == RÖD ) // anses inte vara svart goto Case_D5 ; // C röd && S+D svart // Här är båda syskonbarn == NIL (första iterationen) eller svarta (senare). if ( P -> färg == RÖD ) goto Case_D4 ; // P röd && C+S+D svart
Ombalanseringsslingan för borttagningsoperationen har följande invariant :
-
 I början av varje iteration är den svarta höjden av N lika med iterationstalet minus ett, vilket betyder att den i den första iterationen är noll och att N är en sann svart nod i högre iterationer.
I början av varje iteration är den svarta höjden av N lika med iterationstalet minus ett, vilket betyder att den i den första iterationen är noll och att N är en sann svart nod i högre iterationer. - Antalet svarta noder på vägarna genom N är en mindre än före raderingen, medan det är oförändrat på alla andra vägar, så att det finns en svartöverträdelse vid P om andra vägar finns.
- Alla andra egenskaper (inklusive krav 3 ) är uppfyllda i hela trädet.
Anmärkningar till raderingsdiagrammen
| innan |
fall → |
rotation _ |
uppdrag _ |
efter |
→ nästa |
Δh | ||||||
| P | C | S | D | P | C | S | D | |||||
| — | D1 | → | ||||||||||
| D2 | N := P | ? | ? | 1 | ||||||||
| D3 | P ↶ S | N := N | D6 | 0 | ||||||||
| D5 | 0 | |||||||||||
| D4 | 0 | |||||||||||
| D4 | → | |||||||||||
| D5 | C ↷ S | N := N | D6 | 0 | ||||||||
| D6 | P ↶ S | → | ||||||||||
|
Borttagning: Denna synopsis visar i dess före- kolumner att alla möjliga fall av färgkonstellationer täcks. |
||||||||||||
- I diagrammen nedan används P för N :s förälder, S för syskon till N , C (betyder nära brorson) för S :s barn i samma riktning som N , och D (betyder avlägsen brorson) för S :s annat barn ( S kan inte vara en NIL-nod i den första iterationen, eftersom den måste ha svart höjd ett, vilket var den svarta höjden av N innan dess radering, men C och D kan vara NIL-noder).
- Diagrammen visar den aktuella noden N som det vänstra barnet till dess förälder P även om det är möjligt för N att vara på vardera sidan. Kodexemplen täcker båda möjligheterna med hjälp av sidovariabeln
dir. -
 I början (i den första iterationen) av borttagningen är N NIL-noden som ersätter noden som ska raderas. Eftersom dess placering i förälderns nod är det enda av betydelse, symboliseras den av ( vilket betyder: den nuvarande noden N är en NIL-nod och vänster underordnad) i den vänstra kolumnen i raderingsdiagrammen. När operationen fortskrider kan även korrekta noder (med svart höjd ≥ 1) bli aktuella (se t.ex. fall D2 ).
I början (i den första iterationen) av borttagningen är N NIL-noden som ersätter noden som ska raderas. Eftersom dess placering i förälderns nod är det enda av betydelse, symboliseras den av ( vilket betyder: den nuvarande noden N är en NIL-nod och vänster underordnad) i den vänstra kolumnen i raderingsdiagrammen. När operationen fortskrider kan även korrekta noder (med svart höjd ≥ 1) bli aktuella (se t.ex. fall D2 ). -

 Genom att räkna de svarta kulorna ( och ) i ett raderingsdiagram kan man observera att banorna genom N har en kula mindre än de andra banorna. Detta innebär en svartöverträdelse vid P — om den existerar.
Genom att räkna de svarta kulorna ( och ) i ett raderingsdiagram kan man observera att banorna genom N har en kula mindre än de andra banorna. Detta innebär en svartöverträdelse vid P — om den existerar. - Färgkonstellationen i kolumngruppen före definierar fallet, vars namn anges i kolumnen fallet . Därmed ignoreras möjliga värden i celler som lämnas tomma.
- Raderna i synopsis är ordnade så att täckningen av alla möjliga RB-fall är lätt att förstå.
- Kolumnrotationen anger om en rotation bidrar till ombalanseringen .
- Kolumntilldelningen visar en tilldelning av N innan man går in i ett efterföljande iterationssteg . Detta inducerar möjligen en omtilldelning av de andra noderna P , C , S , D också.
- Om något har ändrats av ärendet visas detta i kolumngruppen efter .
- En pil → i kolumnen härnäst betyder att ombalanseringen är klar med detta steg. Om kolumnen efter bestämmer exakt ett fall, anges detta fall som det efterföljande, annars finns det frågetecken.
- Slingan finns i sektionerna från
Start_Dtill "Radera fall D2" , där problemet med ombalansering eskaleras nivå högre i trädet genom att föräldern P blir den nya strömmen nod N . Så det krävs maximalt iterationer för att reparera trädet (där är trädets höjd). Eftersom sannolikheten för eskalering minskar exponentiellt med varje iteration är den totala ombalanseringskostnaden konstant i genomsnitt, faktiskt avskriven konstant . (Bara som ett undantag: Mehlhorn & Sanders påpekar: "AVL-träd inte konstanta amorterade uppdateringskostnader." Detta är sant för ombalanseringen efter en radering, men inte AVL-insättning.) - Ut ur slingans kropp finns utgående grenar till höljena D3 , D6 , D5 + D6 , D4 och D1 ; sektionen "Radera fall D3" i sig har tre olika utgående grenar till fallen D6 , D5 och D4 .
- Rotationer förekommer i fall D6 och D5 + D6 och D3 + D5 + D6 – alla utanför slingan. Därför förekommer högst tre rotationer totalt.
Ta bort fall D1
Den nuvarande noden N är den nya roten. En svart nod har tagits bort från varje väg, så RB-egenskaperna är bevarade. Trädets svarta höjd minskar med 1.
// Fall_D1 (P == NULL): return ; // raderingen klar
Ta bort fall D2
P , S , och S :s barn är svarta. Efter att ha målat S rött har alla vägar som passerar genom S , vilket är just de vägar som inte går genom N , en svart nod mindre. Nu har alla vägar i underträdet som är rotade av P samma antal svarta noder, men en färre än de vägar som inte går genom P , så krav 4 kan fortfarande överträdas. Efter ommärkning av P till N är slinginvarianten uppfylld så att ombalanseringen kan itereras på en svartnivå (= 1 trädnivå) högre .
// Fall_D2 (P+C+S+D svart): S -> färg = RÖD ; N = P ; // ny aktuell nod (kanske roten) // iterera 1 svartnivå // (= 1 trädnivå) högre } medan (( P = N -> förälder ) != NULL ); // slutet av (do while)-loopen
Ta bort fall D3
Syskonen S är röd, så P och syskonbarnen C och D måste vara svarta. En dir -rotation vid P förvandlar S till N :s morförälder. Sedan efter att ha vänt om färgerna på P och S , är vägen genom N fortfarande kort en svart nod. Men N har en röd förälder P och ett svart syskon S , så transformationerna i fall D4, D5 eller D6 kan återställa RB-formen.
Case_D3 : // S red && P+C+D black: RotateDirRoot ( T , P , dir ); // P kan vara roten P -> färg = RÖD ; S -> färg = SVART ; S = C ; // != NIL // nu: P röd && S svart D = S -> barn [ 1 - dir ]; // avlägsen brorson om ( D != NIL && D -> färg == RÖD ) goto Case_D6 ; // D röd && S svart C = S -> barn [ dir ]; // nära brorson om ( C != NIL && C -> färg == RÖD ) goto Case_D5 ; // C röd && S+D svart // Annars anses C+D vara svart. // faller fram till Case_D4
Ta bort fall D4
Syskonen S och S :s barn är svarta, men P är röd. Att byta färger på S och P påverkar inte antalet svarta noder på vägar som går genom S , men det lägger till en till antalet svarta noder på vägar som går genom N , vilket kompenserar för den borttagna svarta noden på dessa vägar.
Case_D4 : // P röd && S+C+D svart: S -> färg = RÖD ; P -> färg = SVART ; återvända ; // raderingen klar
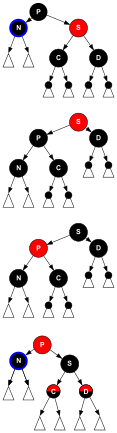
Ta bort fall D5
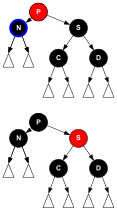
![]() Syskonen S är svart, S :s nära barn C är rött och S :s avlägsna barn D är svart. Efter en
Syskonen S är svart, S :s nära barn C är rött och S :s avlägsna barn D är svart. Efter en (1-dir) -rotation vid S blir brorsonen C S :s förälder och N :s nya syskon. Färgerna på S och C byts ut. Alla banor har fortfarande samma antal svarta noder, men nu N ett svart syskon vars avlägsna barn är rött, så konstellationen passar för fall D6. Varken N eller dess förälder P påverkas av denna transformation, och P kan vara rött eller svart ( i diagrammet).
Case_D5 : // C röd && S+D svart: RotateDir ( S , 1 - dir ); // S är aldrig roten S -> färg = RÖD ; C -> färg = SVART ; D = S ; S = C ; // nu: D röd && S svart // faller igenom till Case_D6
Ta bort fall D6
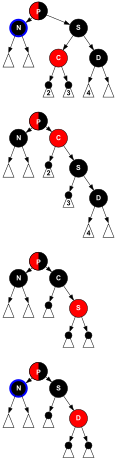
![]() Syskonen S är svart, S :s avlägsna barn D är röd. Efter en
Syskonen S är svart, S :s avlägsna barn D är röd. Efter en dir -rotation vid P blir syskonen S förälder till P och S :s avlägsna barn D . Färgerna P och S byts ut och D görs svart. Hela underträdet har fortfarande samma färg vid sin rot S , nämligen antingen rött eller svart ( i diagrammet), vilket hänvisar till samma färg både före och efter transformationen. På så sätt bevaras krav 3 . Banorna i underträdet som inte går genom N (iow passerar genom D och nod 3 i diagrammet) passerar genom samma antal svarta noder som tidigare, men N har nu ytterligare en svart förfader: antingen har P blivit svart, eller så var det svart och S lades till som svart morförälder. Således passerar banorna som passerar genom N genom ytterligare en svart nod, så att krav 4 återställs och det totala trädet är i RB-form.
Case_D6 : // D red && S black: RotateDirRoot ( T , P , dir ); // P kan vara roten S -> färg = P -> färg ; P -> färg = SVART ; D -> färg = SVART ; återvända ; // radering klar } // slutet av RBdelete2
Eftersom algoritmen transformerar indata utan att använda en extra datastruktur och endast använder en liten mängd extra lagringsutrymme för hjälpvariabler är den på plats .
Bevis på gränser
För finns ett rött–svart träd med höjden med
om jämnt om udda
noder ( är golvfunktionen ) och det finns inget rött-svart träd av denna trädhöjd med färre noder – därför är det minimalt . Dess svarta höjd är (med svart rot) eller för udda (då med en röd rot) också
- Bevis
För att ett rödsvart träd av en viss höjd ska ha minimalt antal noder måste det ha exakt en längsta väg med maximalt antal röda noder, för att uppnå maximal trädhöjd med minimal svart höjd. Förutom denna väg måste alla andra noder vara svarta. Om en nod tas bort från detta träd tappar den antingen höjd eller någon RB-egenskap.
RB-trädet med höjden med röd rot är minimal. Detta överensstämmer med
Ett minimalt RB-träd (RB h i figur 4) med höjden har en rot vars två underträd har olika höjd. Det högre underträdet är också ett minimalt RB-träd, RB h –1 , som också innehåller en längsta väg som definierar dess höjd ; den har noder och den svarta höjden Det andra underträdet är ett perfekt binärt träd med (svart) höjd med svarta noder – och ingen röd nod. Då är antalet noder genom induktion
| (högre underträd) | (rot) | (andra underträdet) | ||||||||
| resulterar i | ||||||||||
| ■ | ||||||||||
Grafen för funktionen är konvex och styckvis linjär med brytpunkter vid h där Funktionen har tabellerats som A027383( h –1) för ( sekvens A027383 i OEIS ).
- Löser funktionen för
Olikheten leder till , vilket för udda leder till
- .
Så i båda, jämna och udda fall, är i intervallet
| (perfekt binärt träd) | (minimalt rött-svart träd) |
där är antalet noder.
- Slutsats
Ett rött-svart träd med noder (nycklar) har trädhöjden
Set operationer och bulk operationer
Förutom operationerna för insättning, radering och uppslagning av ett element har flera uppsättningsoperationer definierats på röd-svarta träd: union , intersection och set difference . Sedan kan snabba bulkoperationer på infogningar eller borttagningar implementeras baserat på dessa inställda funktioner. Dessa uppsättningsoperationer är beroende av två hjälpoperationer, Split och Join . Med den nya verksamheten kan implementeringen av rödsvarta träd bli effektivare och mer parallelliserbar. För att uppnå sin tidskomplexitet kräver denna implementering att roten tillåts vara antingen röd eller svart, och att varje nod lagrar sin egen svarta höjd .
- Join : Funktionen Join finns på två rödsvarta träd t 1 och t 2 och en tangent k , där t 1 < k < t 2 , dvs alla nycklar i t 1 är mindre än k , och alla nycklar i t 2 är större än k . Den returnerar ett träd som innehåller alla element i t 1 , t 2 också som k .
- Om de två träden har samma svarta höjd, skapar Join helt enkelt en ny nod med vänster underträd t 1 , rot k och höger underträd t 2 . Om både t 1 och t 2 har svart rot, ställ in k till rött. Annars sätts k svart.
- Om de svarta höjderna är olika, anta att t 1 har en större svart höjd än t 2 (det andra fallet är symmetriskt). Join följer den högra ryggraden på t 1 tills en svart nod c , som är balanserad med t 2 . Vid denna tidpunkt skapas en ny nod med vänster underordnad c , rot k (inställd på röd) och höger underordnad t 2 för att ersätta c. Den nya noden kan ogiltigförklara den röd-svarta invarianten eftersom högst tre röda noder kan visas i rad. Detta kan fixas med dubbelrotation. Om problemet med dubbelt rött sprider sig till roten ställs roten in på svart, vilket återställer egenskaperna. Kostnaden för denna funktion är skillnaden mellan de svarta höjderna mellan de två ingångsträden.
- Dela : För att dela ett rött-svart träd i två mindre träd, de som är mindre än tangenten x och de större än tangenten x , ritar du först en bana från roten genom att infoga x i det röd-svarta trädet. Efter denna infogning kommer alla värden mindre än x att hittas till vänster om banan, och alla värden större än x kommer att hittas till höger. Genom att tillämpa Join slås alla underträd på vänster sida samman nedifrån och upp med hjälp av tangenter på banan som mellannoder från botten till toppen för att bilda det vänstra trädet, och den högra delen är symmetrisk.
- För vissa applikationer returnerar Split också ett booleskt värde som anger om x visas i trädet. Kostnaden för Split är ordning efter trädets höjd. Denna algoritm har faktiskt ingenting att göra med några speciella egenskaper hos ett röd-svart träd, och kan användas på vilket träd som helst med en join- operation, till exempel ett AVL-träd .
Anslutningsalgoritmen är som följer:
funktion joinRightRB(TL , k, TR ) : om ( TL .color=black) och ( TL .blackHeight= TR .blackHeight): return Node( TL ,⟨k,red⟩, TR ) T '=Node(TL .vänster ,⟨T L .tangent, TL .färg⟩ , joinRightRB(TL .höger ,k,TR ) ) om (TL .color=svart) och (T'.höger. color=T'.right.right.color=red): T'.right.right.color=svart; return rotateLeft(T') return T' /* T ' '[recte T'] */ function joinLeftRB(TL , k, TR ): /* symmetric to joinRightRB */ function join(TL , k, TR ): om TL .blackHeight >T R .blackHeight: T'=joinRightRB(TL , k, TR ) if (T'.color=red) och (T'.right.color=red): T'. color=black return T' if T R .blackHeight>TL .blackHeight : /* symmetrisk */ if (TL .color =black) och (TR .color =black): return Node( TL ,⟨k, röd⟩, TR ) returnod (TL , ⟨k,svart⟩, TR )
Den delade algoritmen är som följer:
funktion split(T, k): if (T = noll) return (noll, false, noll) if (k = T.key) return (T.left, true, T.right) if (k < T.key) : (L',b,R') = split(T.vänster, k) return (L',b,join(R',T.key,T.right)) (L',b,R') = split(T.höger, k) return (join(T.left,T.key,L'),b,T.right)
Föreningen av två röd-svarta träd t 1 och t 2 som representerar mängderna A och B , är ett röd-svart träd t som representerar A ∪ B . Följande rekursiva funktion beräknar denna union:
funktionsunion (t 1 , t 2 ): om t 1 = noll return t 2 om t 2 = noll return t 1 (L 1 ,b,R 1 )=split(t 1 ,t 2 .key) proc1= start : T L =union(L 1 ,t 2 .left) proc2= start : T R =union(R 1 ,t 2 .right) vänta alla proc1,proc2 return join( TL , t 2 .key, TR )
Här antas split returnera två träd: ett som håller tangenterna minus dess inmatningsnyckel, ett håller de större tangenterna. (Algoritmen är oförstörande , men en destruktiv version på plats finns också.)
Algoritmen för korsning eller skillnad är liknande, men kräver Join2- hjälparrutinen som är samma som Join men utan mitttangenten. Baserat på de nya funktionerna för union, korsning eller differens kan antingen en eller flera nycklar infogas i eller raderas från det röd-svarta trädet. Eftersom Split anropar Join men inte hanterar balanseringskriterierna för röd-svarta träd direkt, kallas en sådan implementering vanligtvis för den " join-baserade" implementeringen .
Komplexiteten för var och en av förening, skärningspunkt och skillnad är för två rödsvarta träd i storlekarna och . Denna komplexitet är optimal när det gäller antalet jämförelser. Ännu viktigare, eftersom de rekursiva anropen till union, skärningspunkt eller skillnad är oberoende av varandra, kan de exekveras parallellt med ett parallellt djup . När , har den kopplingsbaserade implementeringen samma beräkningsriktade acykliska graf (DAG) som insättning och radering av ett element om roten av det större trädet används för att dela upp det mindre trädet.
Parallella algoritmer
Parallella algoritmer för att konstruera röd-svarta träd från sorterade listor med objekt kan köras i konstant tid eller tid, beroende på datormodell, om antalet av tillgängliga processorer är asymptotiskt proportionell mot antalet objekt där . Parallella algoritmer för snabb sökning, infogning och radering är också kända.
De sammanfogningsbaserade algoritmerna för röd-svarta träd är parallella för bulkoperationer, inklusive union, korsning, konstruktion, filter, map-reduce, och så vidare.
Parallella bulkoperationer
Grundläggande operationer som infogning, borttagning eller uppdatering kan parallelliseras genom att definiera operationer som bearbetar bulks av flera element. Det är också möjligt att bearbeta bulkar med flera grundläggande operationer, till exempel kan bulks innehålla element att infoga och även element att ta bort från trädet.
Algoritmerna för bulkoperationer är inte bara tillämpliga på det röd-svarta trädet, utan kan också anpassas till andra sorterade sekvensdatastrukturer, som 2–3-trädet, 2–3–4 - trädet och (a,b)-trädet . I det följande kommer olika algoritmer för bulkinsert att förklaras, men samma algoritmer kan även användas för borttagning och uppdatering. Bulkinsert är en operation som infogar varje element i en sekvens i ett träd .
Anslut-baserat
Detta tillvägagångssätt kan tillämpas på alla sorterade sekvensdatastrukturer som stöder effektiva join- och split-operationer. Den allmänna idén är att dela upp och i flera delar och utföra insättningarna på dessa delar parallellt.
- Först måste huvuddelen av element som ska infogas sorteras.
- Efter det delar algoritmen upp i delar av ungefär lika stora.
- måste trädet delar i ett sätt, så att för varje följande begränsningar:
- Nu infogar algoritmen varje element av i sekventiellt. Detta steg måste utföras för varje , vilket kan göras av upp till -processorer parallellt.
- Slutligen kommer de resulterande träden att sammanfogas för att bilda det slutliga resultatet av hela operationen.
Observera att i steg 3 säkerställer begränsningarna för att dela att i steg 5 kan träden sammanfogas igen och den resulterande sekvensen sorteras.
Pseudokoden visar en enkel dela-och-härska-implementering av den kopplingsbaserade algoritmen för bulkinsert. Båda rekursiva anropen kan utföras parallellt. Join-operationen som används här skiljer sig från versionen som förklaras i den här artikeln, istället används join2 , vilket missar den andra parametern k.
bulkInsert (T, I, k): I.sort() bulklInsertRec(T, I, k) bulkInsertRec (T, I, k): if k = 1: forall e in I: T.insert(e) else m : = ⌊storlek(I) / 2⌋ (T 1 , _, T 2 ) := split(T, I[m]) bulkInsertRec(T 1 , I[0 .. m], ⌈k / 2⌉) || bulkInsertRec(T 2 , I[m + 1 .. size(I) - 1], ⌊k / 2⌋) T ← join2(T 1 , T 2 )
Utförandetid
Sortering beaktas inte i denna analys.
| #rekursionsnivåer | |
| T(split) + T(join) | |
| insättningar per tråd | |
| T(infoga) | |
| T(bulkInsert) med = #processorer |
Detta kan förbättras genom att använda parallella algoritmer för delning och sammanfogning. I detta fall är exekveringstiden .
Arbete
| #delar, #ansluter | |
| W(split) + W(join) | |
| #insättningar | |
| W(infoga) | |
| W(bulkInsert) |
Pipelining
En annan metod för att parallellisera bulkoperationer är att använda en pipelining- metod. Detta kan göras genom att dela upp uppgiften att bearbeta en grundläggande operation i en sekvens av deluppgifter. För flera grundläggande operationer kan deluppgifterna bearbetas parallellt genom att tilldela varje deluppgift till en separat processor.
- Först måste huvuddelen av element som ska infogas sorteras.
- För varje element i lokaliserar algoritmen motsvarande infogningsposition i . Detta kan göras parallellt för varje element eftersom inte kommer att muteras i denna process. Nu måste enligt infogningspositionen för varje element. Till exempel är efterföljden av som innehåller de element vars infogningsposition skulle vara till vänster om nod .
- Mellersta elementet i varje efterföljd kommer att infogas i som en ny nod . Detta kan göras parallellt för varje eftersom per definition infogningspositionen för varje är unik. Om innehåller element till vänster eller till höger om , de kommer att finnas i en ny uppsättning av undersekvenser som eller .
-
Nu innehåller möjligen upp till två på varandra följande röda noder i slutet av banorna som bildar roten till bladen, som behöver repareras. Observera att under reparation måste infogningspositionen för elementen Om två noder har olika närmaste svarta förfäder kan de repareras parallellt. Eftersom högst fyra noder kan ha samma närmaste svarta förfader, kan noderna på den lägsta nivån repareras i ett konstant antal parallella steg. Detta steg kommer att tillämpas successivt på svartnivåerna ovan tills är helt reparerat. -
Stegen 3 till 5 kommer att upprepas på de nya undersekvenserna tills är tom. Vid denna tidpunkt har varje element infogats. Varje tillämpning av dessa steg kallas ett stadium . Eftersom längden på undersekvenserna i är och i varje steg halveras undersekvenserna, är antalet steg . Eftersom alla stadier rör sig uppåt i trädets svarta nivåer kan de parallelliseras i en pipeline. När ett steg har bearbetat en svart nivå kan nästa steg flyttas upp och fortsätta på den nivån.
Utförandetid
Sortering beaktas inte i denna analys. Även antas vara mindre än , annars skulle det vara mer effektivt att konstruera det resulterande trädet från början.
| T (hitta infogningsposition) | |
| #etapper | |
| T(insert) + T(reparation) | |
| T(bulkInsert) med ~ #processorer |
|
Arbete
| W(hitta infogningspositioner) | |
| #insättningar, #reparationer | |
| W(insert) + W(reparation) | |
| W(bulkInsert) |
|
Populärkultur
Ett rött-svart träd refererades korrekt i ett avsnitt av Missing som noterades av Robert Sedgewick i en av hans föreläsningar:
-
Jess :Det var den röda dörren igen.
Pollock :Jag trodde att den röda dörren var förvaringsbehållaren.
Jess :Men den var inte röd längre, den var svart.
Antonio :Så vad betyder rött att bli svart?
Pollock :Budgetunderskott, rött bläck, svart bläck.
Antonio :Det kan vara från ett binärt sökträd. Det röd-svarta trädet spårar varje enkel väg från en nod till ett avkomblad som har samma antal svarta noder.
Jess :Hjälper det dig med damerna?
Se även
- Lista över datastrukturer
- Träddatastruktur
- Trädrotation
- AA-träd , en variant av det röd-svarta trädet
- AVL-träd
- B-träd ( 2–3-träd , 2–3–4-träd , B+-träd , B*-träd , UB-träd )
- Syndbock träd
- Splay träd
- T-träd
- WAVL-träd
Referenser och anteckningar
Vidare läsning
- Mathworld: Röd-svart träd
- San Diego State University: CS 660: Red-Black tree notes , av Roger Whitney
- Pfaff, Ben (juni 2004). "Prestandaanalys av BST i systemprogramvara" (PDF) . Stanford University .
externa länkar
- Ben Pfaff: En introduktion till binära sökträd och balanserade träd. Free Software Foundation, Boston 2004, ftp.gnu.org (PDF gzip; 1662 kB)
- En komplett och fungerande implementering i C
- OCW MIT-föreläsning om röd-svarta träd av Erik Demaine
- på YouTube – Visualisering av slumpmässiga och försorterade datainfogningar, i elementära binära sökträd och vänsterlutande röd-svarta träd
- Ett påträngande röd-svart träd skrivet i C++
- Röd-svarta BST i 3.3 Balanced Search Trees
- Röd-svart BST Demo

































































![{\displaystyle {\bigl [}<2\log _{2}(n+1)\;{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0c1043c587524d2a645896481b77387cb1ca96e)

























































