Länka/klippa träd

Länka/klippa träd
Typ	Träd
Uppfunnet	1982
Uppfunnet av	Daniel Dominic Sleator Robert Endre Tarjan
Tidskomplexitet i stor O-notation
Genomsnitt Värsta fall Länk O(log n) amorterad O(log n) Skära O(log n) amorterad O(log n) Väg O(log n) amorterad O(log n) FindRoot O(log n) amorterad O(log n)

Ett länk-/klippträd är en datastruktur för att representera en skog , en uppsättning rotade träd , och erbjuder följande operationer:

• Lägg till ett träd som består av en enda nod till skogen.
• Givet en nod i ett av träden, koppla bort den (och dess underträd) från trädet som den är en del av.
• Fäst en nod till en annan nod som dess underordnade.
• Med en nod, hitta roten till trädet som den tillhör. Genom att göra denna operation på två distinkta noder kan man kontrollera om de tillhör samma träd.

Den representerade skogen kan bestå av mycket djupa träd, så om vi representerar skogen som en vanlig samling av överordnade pekarträd, kan det ta oss lång tid att hitta roten till en given nod. Men om vi representerar varje träd i skogen som ett länk-/avklippt träd, kan vi hitta vilket träd ett element tillhör i O ( log (n)) amorterad amorterad tid. Dessutom kan vi snabbt anpassa samlingen av länk-/kapträd till förändringar i den representerade skogen. I synnerhet kan vi justera det för att slå samman (länk) och dela (klippa) i O (log( n )) amorterad tid.

Länka/klippa träd delar upp varje träd i den representerade skogen i hörn-disjunkta banor, där varje bana representeras av en extra datastruktur (ofta splay trees , även om originalpapperet föregår splay trees och därför använder partiska binära sökträd). Noderna i den extra datastrukturen är ordnade efter deras djup i motsvarande representerade träd. I en variant, naiv partitionering , bestäms banorna av de senast öppnade banorna och noderna, liknande Tango Trees . I partitionering efter storlek bestäms banorna av det tyngsta barnet (barnet med flest barn) i den givna noden. Detta ger en mer komplicerad struktur, men minskar kostnaden för verksamheten från amorterad O(log n) till värsta fall O(log n). Den har användningsområden för att lösa en mängd olika nätverksflödesproblem och för att sända datamängder.

I den ursprungliga publikationen hänvisade Sleator och Tarjan till länk-/kapträd som "dynamiska träd", eller "dynamiska dynoträd".

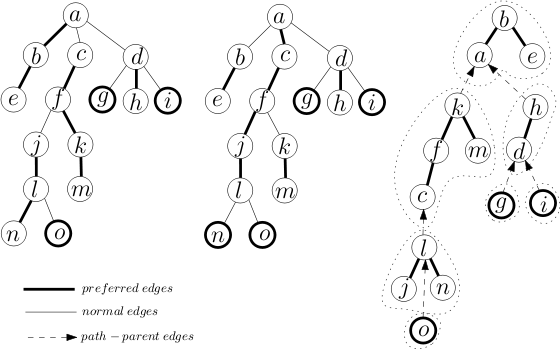
Strukturera

Vi tar ett träd där varje nod har en godtycklig grad av oordnade noder och delar upp det i banor. Vi kallar detta det representerade trädet . Dessa vägar representeras internt av hjälpträd (här kommer vi att använda splayträd), där noderna från vänster till höger representerar vägen från roten till den sista noden på banan. Noder som är anslutna i det representerade trädet som inte är på samma föredragna väg (och därför inte i samma hjälpträd) är anslutna via en väg-förälder-pekare . Denna pekare lagras i roten av hjälpträdet som representerar banan.

Demonstrerar hur noder lagras efter djup i det länkklippta trädet

Föredragna vägar

När en åtkomst till en nod v görs på det representerade trädet , blir den väg som tas den föredragna sökvägen . Det föredragna underordnade av en nod är det sista underordnade som var på åtkomstvägen, eller null om den senaste åtkomsten var till v eller om inga åtkomster gjordes till just denna gren av trädet. En föredragen kant är kanten som förbinder det föredragna barnet med v .

I en alternativ version bestäms föredragna vägar av det tyngsta barnet.

Visar hur ett länkklippt träd förvandlar föredragna stigar till en skog av träd.

Operationer

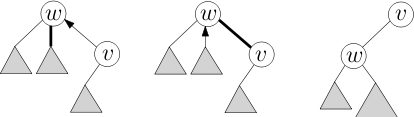
Operationerna vi är intresserade av är FindRoot(Node v), Cut(Node v), Link(Node v, Node w) och Path(Node v). Varje operation implementeras med hjälp av Access(Node v) subrutinen. När vi kommer åt en vertex v ändras den föredragna vägen för det representerade trädet till en väg från roten R på det representerade trädet till noden v . Om en nod på åtkomstvägen tidigare hade ett föredraget underordnat u , och sökvägen nu går till underordnat w , tas den gamla föredragna kanten bort (ändras till en väg-förälder-pekare ), och den nya vägen går nu genom w .

Tillgång

Efter att ha utfört en åtkomst till nod v kommer den inte längre att ha några föredragna underordnade och kommer att vara i slutet av sökvägen. Eftersom noder i hjälpträdet är nycklade efter djup, betyder det att eventuella noder till höger om v i hjälpträdet måste kopplas bort. I ett splayträd är detta en relativt enkel procedur; vi splay på v , vilket för v till roten av hjälpträdet. Vi kopplar sedan bort det högra underträdet av v , vilket är varje nod som kom under den på den tidigare föredragna vägen. Roten till det frånkopplade trädet kommer att ha en väg-förälder-pekare, som vi pekar på v .

Vi går nu uppför det representerade trädet till roten R och bryter och återställer den föredragna banan där det behövs. För att göra detta följer vi path-parent-pekaren från v (eftersom v nu är roten, har vi direkt tillgång till path-parent-pekaren). Om sökvägen som v är på redan innehåller roten R (eftersom noderna är nycklade av djup, skulle det vara noden längst till vänster i hjälpträdet), kommer väg-förälder-pekaren att vara null, och vi är klara med åtkomsten. Annars följer vi pekaren till någon nod på en annan väg w . Vi vill bryta den gamla föredragna vägen för w och återansluta den till vägen v är på. För att göra detta sprider vi på w och kopplar bort dess högra underträd och ställer in dess väg-förälder-pekare till w . Eftersom alla noder är nycklade av djup, och varje nod i vägen för v är djupare än varje nod i vägen för w (eftersom de är barn till w i det representerade trädet), kopplar vi helt enkelt ihop v -trädet som det rätta barnet av w . Vi splay på v igen, som, eftersom v är ett barn av roten w , helt enkelt roterar v till rot. Vi upprepar hela denna process tills väg-förälder-pekaren för v är noll, vid vilken punkt den är på samma föredragna väg som roten till det representerade trädet R .

Under en åtkomst bryts gamla föredragna vägar och ersätts med väg-förälder-pekare, medan den åtkomliga noden sprids till roten av trädet

FindRoot

FindRoot hänvisar till att hitta roten till det representerade trädet som innehåller noden v . Eftersom åtkomstsubrutinen sätter v på den föredragna sökvägen, kör vi först en åtkomst. Nu är noden v på samma föredragna väg, och därmed samma hjälpträd som roten R . Eftersom hjälpträden är nyckelade efter djup, kommer roten R att vara noden längst till vänster i hjälpträdet. Så vi väljer helt enkelt det vänstra barnet av v rekursivt tills vi inte kan gå längre, och denna nod är roten R . Roten kan vara linjärt djup (vilket är värsta fallet för ett splayträd), vi sprider den därför så att nästa åtkomst blir snabb.

Skära

Här skulle vi vilja klippa det representerade trädet vid nod v . Först kommer vi åt v . Detta placerar alla element lägre än v i det representerade trädet som det högra barnet till v i hjälpträdet. Alla element nu i det vänstra underträdet av v är noderna högre än v i det representerade trädet. Vi kopplar därför bort det vänstra barnet av v (som fortfarande bibehåller en anknytning till det ursprungliga representerade trädet genom sin väg-förälder-pekare). Nu v roten till ett representerat träd. Åtkomst till v bryter också den föredragna sökvägen under v , men det underträdet behåller sin anslutning till v genom sin väg-förälder-pekare.

Länk

Om v är en trädrot och w är en vertex i ett annat träd, länka samman träden som innehåller v och w genom att lägga till kanten(v, w), vilket gör w till förälder till v . För att göra detta kommer vi åt både v och w i deras respektive träd, och gör w till vänster underordnat av v . Eftersom v är roten, och noder är nycklade av djupet i hjälpträdet, betyder åtkomst till v att v inte kommer att ha något vänsterbarn i hjälpträdet (eftersom det som rot är det minsta djupet). Att lägga till w som ett vänster underordnat gör det effektivt till förälder till v i det representerade trädet.

Väg

För denna operation vill vi göra någon aggregatfunktion över alla noder (eller kanter) på vägen från rot R till nod v (som "summa" eller "min" eller "max" eller "ökning", etc.). För att göra detta kommer vi åt v , som ger oss ett hjälpträd med alla noder på vägen från rot R till nod v . Datastrukturen kan utökas med data vi vill hämta, såsom min eller max värden, eller summan av kostnaderna i underträdet, som sedan kan returneras från en given väg i konstant tid.

Pseudokod för operationer

 Switch-Preferred-Child(x, y):  om (höger(x) är inte null)  path-parent(höger(x)) = x  höger(x) = y  om (y är inte null)  förälder(y) = x 

 Access(v):  splay(v)  Switch-Preferred-Child(v, null)  if (path-parent(v) är inte null)  w = path-parent(v)  splay(w)  Switch-Preferred-Child(w) , v)  Åtkomst(v) 

 Link(v, w):  Access(v)  Access(w)  left(v) = w  parent(w) = v 

 Cut(v):  Access(v)  if (vänster(v) är inte null)  path-parent(left(v)) = path-parent(v)  left(v) = null  path-parent(v) = null 

Analys

Klipp och länk har O (1) kostnad, plus den för åtkomst. FindRoot har en O (log n ) amorterad övre gräns, plus kostnaden för åtkomsten. Datastrukturen kan utökas med ytterligare information (såsom noden med min eller max värde i dess underträd eller summan), beroende på implementeringen. Således kan Path returnera denna information i konstant tid plus åtkomstgränsen.

Så det återstår att begränsa tillgången för att hitta vår speltid.

Access använder sig av splaying, som vi vet har en O (log n ) amorterad övre gräns. Så den återstående analysen handlar om antalet gånger vi behöver splay. Detta är lika med antalet föredragna underordnade ändringar (antalet kanter som ändrats i den föredragna banan) när vi går uppför trädet.

Vi binder åtkomst genom att använda en teknik som kallas Heavy-Light Decomposition .

Tung-Lätt nedbrytning

Huvudartikel: Nedbrytning av tung väg

Denna teknik kallar en kant tung eller lätt beroende på antalet noder i underträdet. $Size(v)$ representerar antalet noder i underträdet av v i det representerade trädet. En kant kallas tung om storlek(v) > 1 ⁄ 2 storlek(förälder(v)). Således kan vi se att varje nod kan ha högst 1 tung kant. En kant som inte är en tung kant kallas en lätt kant.

Ljusdjupet hänvisar till antalet ljuskanter på en given bana från rot till vertex v . Ljusdjup ≤ lg n eftersom vi varje gång vi korsar en ljuskant minskar antalet noder med minst en faktor 2 (eftersom den kan ha högst hälften av förälderns noder).

Så en given kant i det representerade trädet kan vara vilken som helst av fyra möjligheter: tung-föredragen , tung-oönskad , lätt-föredragen eller lätt-o-föredragen .

Först bevisar vi en $O(\log ^{2}n)$ övre gräns.

O (log ² n ) övre gräns

Åtkomstens spridningsoperation ger oss log n , så vi måste begränsa antalet åtkomster till log n för att bevisa O (log ² n ) övre gränsen.

Varje ändring av föredragen kant resulterar i att en ny föredragen kant bildas. Så vi räknar antalet föredragna kanter som bildas. Eftersom det finns högst stock n kanter som är lätta på en given bana, finns det som mest log n ljusa kanter som ändras till föredragna.

Antalet tunga kanter som blir föredragna kan vara $O(n)$ för varje given operation, men det är $O(\log n)$ amorterad. Under en serie av utföranden kan vi få n -1 tunga kanter att bli föredragna (eftersom det finns högst n -1 tunga kanter totalt i det representerade trädet), men från och med då är antalet tunga kanter som blir att föredra lika med antalet av tunga kanter som blev oönskade vid ett tidigare steg. För varje tung kant som blir oönskad måste en lätt kant bli att föredra. Vi har redan sett att antalet ljusa kanter som kan bli att föredra är högst log n . Så antalet tunga kanter som blir att föredra för m operationer är $m(\log n)+(n-1)$ . Över tillräckligt många operationer ( $m>n-1$ ) blir detta medelvärde till $O(\log n)$ .

Förbättrar till O (log n ) övre gräns

Vi har bundit antalet föredragna underordnade ändringar till ${\displaystyle O(\log n)} ,$ så om vi kan visa att varje föredragen underordnad ändring har kostat O(1) amorterat kan vi binda åtkomstoperationen vid $O(\log n)$ . Detta görs med hjälp av den potentiella metoden .

Låt s(v) vara antalet noder under v i trädet av hjälpträd. Då är potentialfunktionen $\Phi =\summa _{v}\log {s(v)}$ . Vi vet att den amortiserade kostnaden för spridning begränsas av:

$cost(splay(v))\ leq 3\left(\log {s(root(v))}-\log {s(v)}\right)+1$

Vi vet att efter spridning är v barnet till dess väg-föräldernod w . Så vi vet att:

$s(v)\leq s(w)$

Vi använder denna ojämlikhet och den amorterade kostnaden för tillgång för att uppnå en teleskopisk summa som begränsas av:

$3\left(\log {s(R)}-\log {s(v)}\ höger)+O({\text{antal föredragna underordnade ändringar}})$

där R är roten till det representerade trädet, och vi vet att antalet föredragna underordnade ändringar är $O(\log n)$ . s ( R ) = n , så vi har $O(\log n)$ amorterad.

Ansökan

Länk-/klippträd kan användas för att lösa det dynamiska anslutningsproblemet för acykliska grafer. Givet två noder x och y är de sammankopplade om och endast om FindRoot(x) = FindRoot(y). En annan datastruktur som kan användas för samma ändamål är Euler tour tree .

För att lösa problemet med maximalt flöde kan länk-/klippträd användas för att förbättra körtiden för Dinics algoritm från $O(V^{2}E)$ till $O(VE\log V)$ .

Se även

• Splay träd
• Potentiell metod
• Toppträd

Vidare läsning

• Sleator, DD; Tarjan, RE (1983). "En datastruktur för dynamiska träd". Handlingar från det trettonde årliga ACM-symposiet om datorteori - STOC '81 ( PDF) . sid. 114. doi : 10.1145/800076.802464 .
• Sleator, DD; Tarjan, RE (1985). "Självjusterande binära sökträd" (PDF) . Journal of the ACM . 32 (3): 652. doi : 10.1145/3828.3835 .
• Goldberg, AV ; Tarjan, RE (1989). "Hitta minimikostnadscirkulationer genom att avbryta negativa cykler". Journal of the ACM . 36 (4): 873. doi : 10.1145/76359.76368 . – Tillämpning på lägsta kostnadscirkulation
• Link-Cut träd i: föreläsningsanteckningar i avancerade datastrukturer, våren 2012, föreläsning 19. Prof. Erik Demaine, skriftlärare: skriftställare: Justin Holmgren (2012), Jing Jian (2012), Maksim Stepanenko (2012), Mashhood Ishaque (2007) ).
• https://jeffe.cs.illinois.edu/teaching/datastructures/2006/notes/07-linkcut.pdf