Binär hög

Binär (min) hög
Typ	binärt träd/hög
Uppfunnet	1964
Uppfunnet av	JWJ Williams
Tidskomplexitet i stor O-notation
Algoritm Genomsnitt Värsta fall Plats På) På) Sök På) På) Föra in O(1) O(log n) Hitta-min O(1) O(1) Ta bort-min O(log n) O(log n)

Exempel på en komplett binär max-hög

Exempel på en komplett binär min-hög

En binär hög är en högdatastruktur som har formen av ett binärt träd . Binära högar är ett vanligt sätt att implementera prioriterade köer . Den binära högen introducerades av JWJ Williams 1964, som en datastruktur för heapsort .

En binär hög definieras som ett binärt träd med två ytterligare begränsningar:

• Shape-egenskap: en binär hög är ett komplett binärt träd ; det vill säga alla nivåer i trädet, utom möjligen den sista (djupaste) är helt fyllda, och om den sista nivån i trädet inte är komplett fylls noderna på den nivån från vänster till höger.
• Heap-egenskap: nyckeln som lagras i varje nod är antingen större än eller lika med (≥) eller mindre än eller lika med (≤) nycklarna i nodens barn, enligt någon total ordning .

Högar där den överordnade nyckeln är större än eller lika med (≥) de underordnade nycklarna kallas max-högar ; de där det är mindre än eller lika med (≤) kallas min-högar . Effektiva ( logaritmisk tid ) algoritmer är kända för de två operationerna som behövs för att implementera en prioritetskö på en binär hög: infoga ett element och ta bort det minsta eller största elementet från en min-hög respektive maxhög. Binära heaps används också ofta i heapsort- sorteringsalgoritmen , som är en algoritm på plats eftersom binära heaps kan implementeras som en implicit datastruktur , lagra nycklar i en array och använda deras relativa positioner inom den arrayen för att representera relationer mellan barn och förälder. .

Högoperationer

Både infogning och borttagning modifierar högen så att den överensstämmer med formegenskapen först, genom att lägga till eller ta bort från slutet av högen. Sedan återställs högegenskapen genom att gå upp eller ner i högen. Båda operationerna tar O(log n ) tid.

Föra in

För att lägga till ett element till en hög kan vi utföra denna algoritm:

1. Lägg till elementet till den nedre nivån av högen vid det öppna utrymmet längst till vänster.
2. Jämför det tillagda elementet med dess överordnade; om de är i rätt ordning, sluta.
3. Om inte, byt elementet med dess överordnade och återgå till föregående steg.

Steg 2 och 3, som återställer heap-egenskapen genom att jämföra och eventuellt byta en nod med dess överordnade, kallas för upp-hög- operationen (även känd som bubbla-up , percolate-up , sikta upp , trickle-up , simma- up , heapify-up , eller cascade-up ).

Antalet operationer som krävs beror endast på antalet nivåer det nya elementet måste stiga för att tillfredsställa heap-egenskapen. Således har insättningsoperationen en tidskomplexitet i värsta fall av O( logn ) . För en slumpmässig hög, och för upprepade infogningar, har infogningsoperationen en medelfallskomplexitet på O(1).

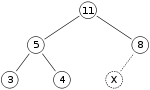
Som ett exempel på binär heap-insättning, säg att vi har en max-heap

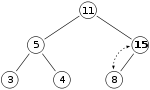
och vi vill lägga till siffran 15 till högen. Vi placerar först 15:an i positionen markerad med X. Men heap-egenskapen bryts eftersom 15 > 8 , så vi måste byta 15:an och 8:an. Så, vi har heapen som ser ut som följer efter det första bytet:

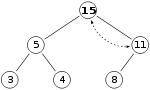
Men heap-egenskapen är fortfarande bruten sedan 15 > 11 , så vi måste byta igen:

vilket är en giltig max-heap. Det finns ingen anledning att kontrollera det vänstra barnet efter detta sista steg: i början var max-högen giltig, vilket innebär att roten redan var större än dess vänstra underordnade, så att ersätta roten med ett ännu högre värde kommer att behålla egenskapen som varje nod är större än dess barn ( 11 > 5 ; om 15 > 11 och 11 > 5 , då 15 > 5 , på grund av den transitiva relationen ).

Extrahera

Proceduren för att ta bort roten från högen (effektivt extrahera det maximala elementet i en max-hög eller det minsta elementet i en min-hög) med bibehållande av heap-egenskapen är som följer:

1. Byt ut roten av högen med det sista elementet på den sista nivån.
2. Jämför den nya roten med dess barn; om de är i rätt ordning, sluta.
3. Om inte, byt elementet med ett av dess underordnade element och återgå till föregående steg. (Byt med sitt mindre barn i en min-hög och sitt större barn i en max-hög.)

Steg 2 och 3, som återställer heap-egenskapen genom att jämföra och eventuellt byta en nod med ett av dess barn, kallas down -heap (även känd som bubble-down , percolate-down , sila-down , sink-down , trickle ned , heapify-down , cascade-down , extrahera-min eller extrahera-max , eller helt enkelt heapify ) operation.

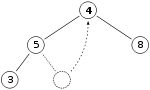
Så, om vi har samma max-hög som tidigare

Vi tar bort 11:an och ersätter den med 4:an.

Nu är heap-egenskapen bruten eftersom 8 är större än 4. I det här fallet räcker det att byta de två elementen, 4 och 8, för att återställa heap-egenskapen och vi behöver inte byta element ytterligare:

Den nedåtgående noden byts ut med den större av dess barn i en max-hög (i en min-hög skulle den bytas ut med sin mindre underordnade), tills den uppfyller högegenskapen i sin nya position. Denna funktionalitet uppnås av Max-Heapify -funktionen som definieras nedan i pseudokod för en arraybackad heap A med längdlängd ( A ). A indexeras från 1.

    
    
      

      
    
        // Utför en ned-hög eller heapify-down-operation för en max-heap //  A  : en array som representerar högen, indexerad med början på 1 // i  :  indexet som ska börja vid när du heapify ner  Max-Heapify  (  A  ,  i  ):  vänster  ← 2×  i  höger  ← 2×  i  + 1  största  ←  i  om  vänster  ≤  längd  (  A  )  och  A  [  vänster  ] > A[  störst  ]  sedan  :  störst  ←  vänster  om  höger  ≤  längd  (  A  )  och  A  [  höger  ] >  A  [  största  ]  sedan  :  störst  ←  höger  om  störst  ≠  i  då  :  byt ut  A  [  i  ] och  A  [  störst  ]  Max-Heapify  (  A  ,  störst  ) 

För att ovanstående algoritm ska kunna återupphöja arrayen korrekt, kan inga noder förutom noden vid index i och dess två direkta barn bryta mot heap-egenskapen. Ned-hög-operationen (utan föregående swap) kan också användas för att ändra värdet på roten, även när ett element inte tas bort.

I värsta fall måste den nya roten bytas ut med sitt underordnade på varje nivå tills den når bottennivån i högen, vilket innebär att raderingsoperationen har en tidskomplexitet i förhållande till trädets höjd, eller O(log n ) ).

Sätt i och extrahera

Att infoga ett element och sedan extrahera från högen kan göras mer effektivt än att bara anropa infognings- och extraheringsfunktionerna som definierats ovan, vilket skulle involvera både en upheap- och downheap -operation. Istället kan vi bara göra en downheap -operation, enligt följande:

1. Jämför om objektet vi trycker eller den kikade toppen av högen är större (förutsatt att en maxhög är hög)
2. Om roten av högen är större:
   1. Ersätt roten med det nya objektet
   2. Höga ner med början från roten
3. Annars, returnera varan vi trycker på

Python tillhandahåller en sådan funktion för insättning och sedan extraktion som kallas "heappushpop", som omskrivs nedan. Högarrayen antas ha sitt första element vid index 1.

    // Skjut ett nytt objekt till en (max) hög och extrahera sedan roten av den resulterande högen. //   heap  : en array som representerar högen, indexerad till 1 //  item  : ett element att infoga // Returnerar den största av de två mellan  objekt  och roten av  heap  .  Push-Pop  (  heap  : List<T>,  item  : T) -> T:  om  heap  inte är tom  och  heap[1] >  objekt  då  : // < if min heap  swap  heap  [1] och  item  _downheap(  heap  startande från index 1  )  returvara  

En liknande funktion kan definieras för att poppa och sedan infoga, som i Python kallas "heapreplace":

   // Extrahera roten av högen, och tryck ett nytt objekt //  heap  : en array som representerar högen, indexerad till 1 //  item  : ett element att infoga // Returnerar den aktuella roten av  heap  Ersätt  (  heap  : List<T >,  artikel  : T) -> T:  byt  hög  [1] och  artikel  _downheap(  hög  från index 1)  returnera  artikel 

Sök

Att hitta ett godtyckligt element tar O(n) tid.

Radera

Att ta bort ett godtyckligt element kan göras på följande sätt:

1. Hitta index $i$ för elementet vi vill ta bort
2. Byt ut detta element med det sista elementet
3. Down-heapify eller up-heapify för att återställa heap-egenskapen. I en max-heap (min-heap) krävs up-heapify endast när den nya nyckeln för element $i$ är större (mindre) än den föregående eftersom endast heap-egenskapen för det överordnade elementet kan vara kränkts. Om man antar att heap-egenskapen var giltig mellan element $i$ och dess underordnade före elementbytet, kan den inte kränkas av ett nu större (mindre) nyckelvärde. När den nya nyckeln är mindre (större) än den tidigare krävs bara en ned-heapify eftersom heap-egenskapen bara kan kränkas i de underordnade elementen.

Minska eller öka knapp

Minskningsnyckeloperationen ersätter värdet på en nod med ett givet värde med ett lägre värde, och ökningsnyckeloperationen gör detsamma men med ett högre värde. Detta innebär att hitta noden med det givna värdet, ändra värdet och sedan ned-heapify eller up-heapifying för att återställa heap-egenskapen.

Minska nyckel kan göras på följande sätt:

1. Hitta indexet för elementet vi vill ändra
2. Minska nodens värde
3. Ned-heapify (förutsatt en max-hög) för att återställa heap-egenskapen

Öka nyckel kan göras på följande sätt:

1. Hitta indexet för elementet vi vill ändra
2. Öka nodens värde
3. Up-heapify (förutsatt en max heap) för att återställa heap-egenskapen

Bygger en hög

Att bygga en hög från en array med n ingångselement kan göras genom att börja med en tom hög och sedan successivt infoga varje element. Det här tillvägagångssättet, kallat Williams metod efter uppfinnaren av binära högar, kan lätt ses köra i O ( n log n ) tid: den utför n insättningar till O (log n ) kostnad vardera.

Williams metod är dock suboptimal. En snabbare metod (på grund av Floyd ) börjar med att godtyckligt placera elementen på ett binärt träd, med respekt för formegenskapen (trädet kan representeras av en array, se nedan). Börja sedan från den lägsta nivån och rör dig uppåt, sålla roten av varje underträd nedåt som i raderingsalgoritmen tills heap-egenskapen återställs. Mer specifikt om alla underträd som börjar på någon höjd $h$ redan har "heapified" (den lägsta nivån som motsvarar $h=0$ ), träden på höjden $h +1$ kan heapifieras genom att skicka sin rot längs vägen för maximalt värderade barn när man bygger en max-hög, eller minst värderade barn när man bygger en min-hög. Denna process tar $O(h)$ operationer (swaps) per nod. I denna metod sker det mesta av upphopningen i de lägre nivåerna. Eftersom höjden på högen är ${\displaystyle \lfloor \log n\rfloor } ,$ är antalet noder på höjden $h$$\leq {\frac {2^{\lfloor \log n\rfloor }}{2^{h}}}\leq {\frac {n}{2^{h}}}$ . Därför är kostnaden för att heapify alla underträd:

${\ displaystyle {\begin{aligned}\sum _{h=0}^{\lfloor \log n\rfloor }{\frac {n}{2^{h}}}O(h)&=O\left(n \sum _{h=0}^{\lfloor \log n\rfloor }{\frac {h}{2^{h}}}\right)\\&=O\left(n\summa _{h= 0}^{\infty }{\frac {h}{2^{h}}}\right)\\&=O(n)\end{aligned}}}$

Detta använder det faktum att den givna oändliga serien ${\textstyle \sum _{i=0}^{\infty }i/2^{i}}$ konvergerar .

Det exakta värdet av ovanstående (det värsta antalet jämförelser under högkonstruktionen) är känt för att vara lika med:

$2n-2s_{2}(n)-e_{2}(n)$ ,

där s ₂ ( n ) är summan av alla siffror i den binära representationen av n och e ₂ ( n ) är exponenten för 2 i primtalsfaktoriseringen av n .

Det genomsnittliga fallet är mer komplext att analysera, men det kan visas att det asymptotiskt närmar sig 1,8814 n − 2 log ₂ n + O (1) jämförelser.

Build -Max-Heap- funktionen som följer konverterar en array A som lagrar ett komplett binärt träd med n noder till en max-heap genom att upprepade gånger använda Max-Heapify (ned-heapify för en max-heap) på ett nedifrån-och-upp-sätt . Matriselementen indexerade med våning ( n /2) + 1 , våning ( n /2) + 2 , ..., n är alla löv för trädet (förutsatt att index börjar på 1) - så var och en är ett enelement högen och behöver inte hophopas. Build-Max-Heap kör Max-Heapify på var och en av de återstående trädnoderna.

  
         Bygg-Max-Hög  (  A  ):  för varje  index  i  från  golv  (  längd  (  A  )/2)  ner till  1  gör:  Max-Heapify  (  A  ,  i  ) 

Hög implementering

Ett litet komplett binärt träd lagrat i en array

Jämförelse mellan en binär hög och en arrayimplementering.

Heaps implementeras vanligtvis med en array . Vilket binärt träd som helst kan lagras i en array, men eftersom en binär hög alltid är ett komplett binärt träd kan den lagras kompakt. Inget utrymme krävs för pekare ; istället kan föräldern och barnen för varje nod hittas med aritmetik på matrisindex. Dessa egenskaper gör denna heapimplementering till ett enkelt exempel på en implicit datastruktur eller Ahnentafel -lista. Detaljerna beror på rotpositionen, vilket i sin tur kan bero på begränsningar för ett programmeringsspråk som används för implementering, eller programmerares preferenser. Specifikt, ibland placeras roten vid index 1, för att förenkla aritmetiken.

Låt n vara antalet element i högen och i vara ett godtyckligt giltigt index för den matris som lagrar högen. Om trädroten är vid index 0, med giltiga index 0 till n − 1, så har varje element a vid index i

• barn vid index 2 i + 1 och 2 i + 2
• dess förälder vid indexgolvet ( ( i − 1) / 2).

Alternativt, om trädroten är vid index 1, med giltiga index 1 till n , så har varje element a vid index i

• barn vid index 2 i och 2 i +1
• dess förälder vid indexgolvet ( i / 2).

Denna implementering används i heapsort -algoritmen som återanvänder det utrymme som tilldelats indatamatrisen för att lagra heapen (dvs. algoritmen görs på plats ). Denna implementering är också användbar som en prioritetskö . När en dynamisk array används är det möjligt att infoga ett obegränsat antal objekt.

Upheap- eller downheap -operationerna kan sedan anges i termer av en array enligt följande: anta att heapegenskapen gäller för indexen b , b +1, ... , e . Sift-down-funktionen utökar heap-egenskapen till b −1, b , b +1, ..., e . Endast index i = b −1 kan bryta mot heap-egenskapen. Låt j vara indexet för det största barnet av a [ i ] (för en max-hög, eller det minsta barnet för en min-hög) inom intervallet b , ..., e . (Om inget sådant index existerar eftersom 2 i > e så gäller heap-egenskapen för det nyligen utökade intervallet och ingenting behöver göras.) Genom att byta värdena a [ i ] och a [ j ] etableras heap-egenskapen för position i . Vid denna tidpunkt är det enda problemet att heap-egenskapen kanske inte håller för index j . Sift-down-funktionen tillämpas svansrekursivt på index j tills heap-egenskapen är etablerad för alla element.

Sållningsfunktionen är snabb. I varje steg behövs bara två jämförelser och ett byte. Indexvärdet där det fungerar fördubblas i varje iteration, så att som mest log ₂ e steg krävs.

För stora högar och användning av virtuellt minne är det ineffektivt att lagra element i en array enligt ovanstående schema: (nästan) varje nivå finns på en annan sida . B-högar är binära högar som håller underträd på en enda sida, vilket minskar antalet sidor som nås med upp till en faktor tio.

Operationen att slå samman två binära högar tar Θ( n ) för lika stora högar. Det bästa du kan göra är (vid arrayimplementering) helt enkelt att sammanfoga de två heap-arrayerna och bygga en heap av resultatet. En heap på n element kan slås samman med en heap på k element genom att använda O(log n log k ) nyckeljämförelser, eller, i fallet med en pekarbaserad implementering, i O(log n log k ) tid. En algoritm för att dela upp en hög på n element i två högar på k- respektive nk -element, baserad på en ny syn på högar som en ordnad samling av underhögar, presenterades i. Algoritmen kräver O(log n * log n ) jämförelser. Vyn presenterar också en ny och konceptuellt enkel algoritm för att slå samman högar. När sammanslagning är en vanlig uppgift rekommenderas en annan heapimplementering, till exempel binomial heaps , som kan slås samman i O(log n ).

Dessutom kan en binär hög implementeras med en traditionell binär träddatastruktur, men det finns ett problem med att hitta det intilliggande elementet på den sista nivån på den binära högen när man lägger till ett element. Detta element kan bestämmas algoritmiskt eller genom att lägga till extra data till noderna, kallat "trådning" av trädet – istället för att bara lagra referenser till barnen lagrar vi nodens efterföljare i ordningsföljd också .

Det är möjligt att modifiera högstrukturen för att göra utvinningen av både det minsta och största elementet möjligt i $O$$(\log n)$ tid. För att göra detta växlar raderna mellan minhög och maxhög. Algoritmerna är ungefär desamma, men i varje steg måste man överväga de alternerande raderna med alternerande jämförelser. Prestandan är ungefär densamma som en vanlig enkelriktningshög. Denna idé kan generaliseras till en min-max-medianhög.

Härledning av indexekvationer

I en arraybaserad heap kan barnen och föräldern till en nod lokaliseras via enkel aritmetik på nodens index. Det här avsnittet härleder de relevanta ekvationerna för högar med roten vid index 0, med ytterligare anteckningar om högar med roten vid index 1.

För att undvika förvirring kommer vi att definiera nivån för en nod som dess avstånd från roten, så att själva roten upptar nivå 0.

Barnnoder

För en generell nod som ligger vid index i (som börjar från 0), kommer vi först att härleda indexet för dess högra underordnade, ${\text{right}}=2i+2$ .

Låt nod i vara placerad på nivå L och notera att vilken nivå l som helst innehåller exakt $2^{l}$ noder. Dessutom finns det exakt $2^{l+1}-1$ noder i lagren upp till och inklusive lager l (tänk på binär aritmetik; 0111...111 = 1000.. 0,000 - 1). Eftersom roten är lagrad vid 0, kommer den k: te noden att lagras i index $(k-1)$ . Att sätta ihop dessa observationer ger följande uttryck för indexet för den sista noden i lager l .

${\text{last}}(l)=(2^{l+1}-1)-1= 2^{l+1}-2$

Låt det finnas j -noder efter nod i i lager L, så att

${\begin{alignedat}{2}i=&\quad {\text{last}}(L)-j\\ =&\quad (2^{L+1}-2)-j\\\end{aligned}}$

Var och en av dessa j -noder måste ha exakt 2 barn, så det måste finnas $2j$ -noder som skiljer i :s högra underordnade från slutet av dess lager ( ${\displaystyle L+1})$ .

${\begin{alignedat }{2}{\text{höger}}=&\quad {\text{last(L + 1)}}-2j\\=&\quad (2^{L+2}-2)-2j\\ =&\quad 2(2^{L+1}-2-j)+2\\=&\quad 2i+2\end{alignedat}}$

Såsom krävs.

När vi noterar att det vänstra underordnade underordet av en nod alltid är 1 plats före dess högra underordnade, får vi ${\text{left}}=2i+1$ .

Om roten ligger vid index 1 istället för 0, är ​​den sista noden på varje nivå istället på index $2^{l+1}-1$ . Genom att använda detta genomgående ger ${\text{left}}=2i$ och ${\text{right}}=2i+1$ för högar med roten vid 1 .

Föräldernod

Varje nod är antingen vänster eller höger barn till sin förälder, så vi vet att något av följande är sant.

1. $i=2\ gånger ({\text{förälder}})+1$
2. $i=2\ gånger ({\text{förälder}})+2$

Därav,

${\text{förälder}}={\frac {i-1}{2}}\;{\textrm {eller}}\;{\frac {i -2}{2}}$

Betrakta nu uttrycket $\left\lfloor {\dfrac {i-1}{2}}\right\rfloor$ .

Om nod $i$ är ett vänsterunderordnat, ger detta resultatet direkt, men det ger också rätt resultat om nod $i$ är ett högerunderordnat. I det här fallet måste ${\displaystyle (i-2)} vara jämnt, och därför måste$$(i-1)$ vara udda.

${\begin{alignedat}{2}\left\lfloor {\dfrac {i-1}{2} }\right\rfloor =&\quad \left\lfloor {\dfrac {i-2}{2}}+{\dfrac {1}{2}}\right\rfloor \\=&\quad {\frac { i-2}{2}}\\=&\quad {\text{förälder}}\end{alignedat}}$

Därför, oavsett om en nod är ett vänster eller höger barn, kan dess förälder hittas av uttrycket:

${\text{parent}}=\left\lfloor {\dfrac {i-1}{2}}\right\rfloor$

Relaterade strukturer

Eftersom ordningen av syskon i en heap inte specificeras av heap-egenskapen, kan en enda nods två barn bytas ut fritt om det inte bryter mot formegenskapen (jämför med treap ) . Notera dock att i den gemensamma array-baserade högen, att helt enkelt byta barn kan också behöva flytta barnens sub-trädnoder för att behålla heap-egenskapen.

Den binära högen är ett specialfall av den d-ära högen där d = 2.

Sammanfattning av löptider

Här är tidskomplexiteten för olika högdatastrukturer. Funktionsnamn antar en min-hög. För betydelsen av " O ( f )" och " Θ ( f )" se Big O-notation .

Drift	hitta-min	radera-min	Föra in	minska-knappen	smälta samman
Binär	Θ (1)	Θ (log n )	O (log n )	O (log n )	Θ ( n )
Vänsterman	Θ (1)	Θ (log n )	Θ (log n )	O (log n )	Θ (log n )
Binom	Θ (1)	Θ (log n )	Θ (1)	Θ (log n )	O (log n )
Fibonacci	Θ (1)	O (log n )	Θ (1)	Θ (1)	Θ (1)
Parning	Θ (1)	O (log n )	Θ (1)	o (log n )	Θ (1)
Brodal	Θ (1)	O (log n )	Θ (1)	Θ (1)	Θ (1)
Rank-parning	Θ (1)	O (log n )	Θ (1)	Θ (1)	Θ (1)
Strikt Fibonacci	Θ (1)	O (log n )	Θ (1)	Θ (1)	Θ (1)
2–3 högar	O (log n )	O (log n )	O (log n )	Θ (1)	?

Se även

• Högen
• Heapsort

externa länkar

• Öppna datastrukturer - Avsnitt 10.1 - BinaryHeap: An Implicit Binary Tree , Pat Morin
• Implementering av binär maxhög i C av Robin Thomas
• Implementering av binär min heap i C av Robin Thomas