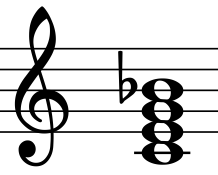Vogels Tonnetz
Vogel's Tonnetz är en grafisk och matematisk representation av skalområdet för just intonation , introducerad av den tyske musikteoretikern Martin Vogel 1976 i hans bok Die Lehre von den Tonbeziehungen (engelska: On the Relations of Tone, 1993). Den grafiska representationen är baserad på Eulers Tonnetz , som lägger till en tredje dimension för bara sjundedelar till de två dimensionerna för bara femtedelar och bara tredjedelar . Den tjänar till att illustrera och analysera ackord och deras relationer. Den fyrdimensionella matematiska representationen inklusive oktaver möjliggör utvärdering av överensstämmelsen mellan övertoner i ackord beroende på tonmaterialet. Det kan därmed också tjäna till att bestämma det optimala tonala materialet för ett visst ackord.
Den grafiska representationen
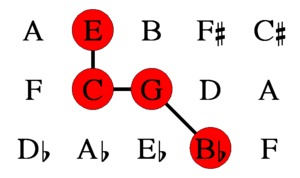
Den grafiska representationen av Vogels Tonnetz är begränsad till de tre dimensionerna för femma, tredjedelar och sjunde. I denna representation visas toner åtskilda av en eller flera oktaver på samma noder. Illustrationen visar ackordet som är det vanligaste 4-toners ackord i västerländsk musik: den dominanta septiman. I Eulers Tonnetz är B-lägenheten uppbyggd av femmor och tredjedelar. I Vogels Tonnetz ges den som en rättvis harmonisk sjua.
Representationen av detta ackord i Vogels tredimensionella Tonnetz gör dess statistiska dominans mycket mer rimlig än dess representation i Eulers tvådimensionella Tonnetz: Det finns en distinkt referensnot (C), och alla andra toner är kopplade till denna referensnot via enkel ettstegsintervaller i denna Tonnetz.
Den matematiska representationen
Den matematiska representationen av Vogels Tonnetz är fyrdimensionell, även med tanke på oktaver . Varje ton representeras av en fyrdubbling av siffror som anger hur många oktaver, "femtedelar", "tredjedelar" och "sjunde" som behövs för att nå den tonen i Tonnetz (där termerna "femtedelar", "tredjedelar" och "sjundedel) " beteckna primtalen 3, 5 och 7, istället för intervallen 3/2, 5/4 och 7/4). C-dur septimackordet med tonerna c', e', g' och b-flat' skulle (med hänvisning till C) kunna representeras av siffrorna 4, 5, 6 och 7. Detta motsvarar fyrfalden ( 2,0,0,0), (0,0,1,0), (1,1,0,0) och (0,0,0,1). De fyrdubbla notationerna representerar primtalsuppdelningen av de tal som behövs för att beskriva ackordet, begränsat till de fyra första primtalen.
Arthur von Oettingens harmoniska dualism , där dur- och mollackord är spegelbilder av varandra. Denna uppfattning kompletteras med en kvantitativ beräkning av konsonansvärden (eller snarare dissonansvärden ).
För detta ändamål introducerar Vogel virtuella referenstoner som inte nödvändigtvis är en del av ackordet. Dessa referenstoner väljs så att alla ackordtoner har heltalsrelationer till dessa referenstoner. För varje ackord finns det en lägre och en övre referenston, där alla ackordtoner är heltalsmultipler av frekvensen för den undre referenstonen och heltalsfraktioner av frekvensen för den övre referenstonen. I fyrfaldig notation finns det bara positiva (eller noll) värden om ackordet är relaterat till den lägre referenstonen, och endast negativa (eller noll) värden om ackordet är relaterat till den högre referenstonen.
För att få ett enda numeriskt värde som beskriver komplexiteten i ett ackord, bygger Vogel en viktad summa av de fyrdubblar som beskriver ackordets toner. Han föreslår vikterna 1, 3, 5 och 7 för primtalen 2, 3, 5 och 7. Vogel avvisar den mer uppenbara varianten där primtal 2 viktas med 2 eftersom det leder till resultat som enligt hans mening inte gör det följa uppfattningen hos musikaliskt skickliga lyssnare. Slutligen delas den viktade summan med antalet toner i ackordet. Denna beräkning görs för både den högre och den lägre referenstonen. Beroende på vilket av dessa två värden som är mindre, märks ackordet sedan som "Oberklang" eller "Unterklang" ("övre ackord", om referens till den nedre referensnoten, eller "nedre ackord", om det refereras till den övre referensnoten ).
C-durackordet c'-e'-g' skulle till exempel kunna refereras till C. Alla tre toner i treklangen kan representeras som heltalsmultiplar av frekvensen för denna referenston (4, 5 och 6). Den primära sönderdelningen ger 2·2,5,2·3. Genom att tillämpa de vikter som Vogel föreslår får man ett så kallat konsonansvärde på (1+1+5+1+3)/3 = 11/3 = 3,67. Samma ackord kan också refereras till b'''': denna övre referenston har 15 gånger frekvensen av c', 12 gånger frekvensen av e' och tio gånger frekvensen av g'. Den primära sönderdelningen ger3·5,2·2·3,2·5. Konsonansvärdet beräknas till (3+5+1+1+3+1+5)/3 = 19/3 = 6,33. Eftersom konsonansvärdet för den nedre referenstonen är bättre (mindre), definieras c-durackordet c'-e'-g' som ett övre ackord som refereras till C. Konsonansvärdet för c-molakkordet c'-es '-g' är identisk. Det är dock en referens till den övre referenstonen i detta ackord, g'''. Följaktligen förkastar Vogel namngivningen av detta ackord som C-moll eftersom dess referensnot inte är C utan G. Han kallar det "G lägre ackord".
Vogel föreslår en specifik notation för övre och nedre ackord. Notationen börjar med att beteckna referenstonen med gemener. Övre ackord är markerade med ett "O" (Oberklang) och betecknas från vänster till höger, nedre ackord är markerade med ett "U" (Unterklang) och betecknas från höger till vänster. C-durackordet betecknas som cO, C-molakkordet betecknas som Ug. Ytterligare symboler för ytterligare toner (7 för att lägga till en övre eller nedre septima) läggs till till vänster eller till höger, beroende på om det är ett övre eller ett nedre ackord. C 7 ackordet som avbildas ovan skulle betecknas som cO7.
Förutom beräkningen av konsonansvärden för enstaka ackord, föreslår Vogel en beräkning av konsonansen för ackordövergångar. När man övergår från ett n-tons ackord till ett m-not ackord utvärderas alla N·M not-till-not övergångar via primtalsupplösning och viktad summa, och ett medelvärde för alla dessa övergångar beräknas. Vogel föreslår också att man beräknar ett konsonansvärde för ett helt musikstycke, med hänsyn till en central referenspunkt som liknar en slutlig .
Konsonans och övertoners kongruens
Konsonansvärdet beräknat med Vogels formel bör snarare kallas dissonansvärde, eftersom med ökande dissonans av ett ackord eller intervall dess värde ökar. Vogel gjorde inte anspråk på att förutsäga konsonansbedömningar av dagens lyssnare. En nära relation mellan Vogels konsonansvärden och konsonansbedömningar är i själva verket inte att vänta. För det första korrelerar konsonansbedömningar starkt med förtrogenhetsbedömningar. För det andra tillskrivs dur och moll känslomässiga värden av dagens västerländska lyssnare (minor uppfattas som uttryck för sorg). För det tredje tar hans formel endast hänsyn till övertonernas kongruens, men inte kongruensen av kombinationstoner . Det skulle vara mer försiktigt att säga att Vogels formel korrelerar med övertonernas kongruens, vilket uttrycker hur långt övertonerna i ett ackord passar ihop eller inte.
Räckvidden för formelns giltighet begränsas dessutom av hörselns gränser. En rättvis oktav kan inte särskiljas från en oktav som är felinställd av en schisma (en felinställning på cirka 2 cent ). Den perceptuella gränsen för frekvensskillnaden för komplexa toner är cirka 0,25 % (4 cent). Vogels konsonansformel ger ett konsonansvärde på (1·1+0·3+0·5+0·7)/2 = 0,5 för den bara oktaven (1,0,0,0) och ett värde på (14· 1+8·3+1·5+0·7)/2 = 43/2 = 21,5 för oktaven felstämd av ett skisma (-14,8,1,0).
Konsekvenser för valet av toner
Vogels konsonansformel kan hjälpa till att avgöra vilka toner av Tonnetz som ska tas för ett visst ackord. Konsonansvärdet för det sjunde ackordet i Eulers Tonnetz (se figuren ovan) är 8,5. I Vogels Tonnetz kunde man välja samma toner, vilket resulterade i samma konsonansvärde. Om man däremot bestämmer sig för att välja den bara sjunde, förbättras konsonansvärdet till 4,5. Därför, enligt Vogel, är det septimackord som använder en bara septim att föredra framför ett septimackord där septim är uppbyggt av kvint och terts.
Kompositionella konsekvenser
Vogel hävdar att hans formel också medför kompositionskonsekvenser. Om man vill att ett ackord ska vara konsonant, bör durackord komponeras så att terts och septim ställs i ett högt register. Mindre ackord skulle dock behöva sättas åt andra hållet, med tertsar och septivar i ett lågt register. Detta är på intet sätt förenligt med de senaste århundradenas kompositionspraxis (med kanske undantag för Tristan-ackordet, se nedan). Som en följd av detta låter mindre ackord inställda efter Vogels kompositionsregler obekanta. De uppvisar dock en bättre övertonskongruens än deras klassiska varianter. Den vänstra handen av de två c-mollackorden i den angränsande figuren är komponerad på klassiskt sätt, där den tredje är satt i ett högregister. Konsonansvärdet för detta ackord är 4,33. Det högra mollackordet har en låg terts. Det låter obekant. Dess konsonansvärde är dock mycket lägre (3,0), och kongruensen för dess övertoner är mycket bättre.
Att begränsa teorin till primtalen 2, 3, 5 och 7
Vogel betraktar det teoretiskt oändliga fyrdimensionella tonutrymmet i hans Tonnetz som komplett; inga ytterligare dimensioner behövs för högre primtal. Enligt hans teori är konsonans resultatet av övertonens kongruens . Primtalet 11 och något annat högre primtal kan inte leda till någon uppfattning om kongruens, eftersom innerörat endast separerar de första åtta till tio partierna. Den elfte partialen kan vara hörbar och urskiljbar från den tionde eller tolfte partialen om den isoleras via tekniker som flageolet . Om de presenteras som en del av en komplex ton som även omfattar de angränsande partialerna, skulle dessa partialer smälta samman, och en överensstämmelse med partialen av en annan ton kunde inte längre upptäckas. Det kan vara intressant att testa om det är möjligt att detektera harmonisk kongruens för högre primtal för instrument med udda partialer, eftersom avstånden mellan partialer är högre i dessa instrument. Med träning kan det vara möjligt att detektera konsonans upp till primtal 17 eller till och med 19.
Det halvt förminskade sjundeackordet i Vogels Tonnetz
Tristanackordet är ett historiskt viktigt ackord i Richard Wagners opera Tristan och Isolde . Dess roll i funktionell harmoni kan inte klart fastställas. Den anses vara tonmässigt orolig och extremt kromatisk.
I Vogel's Tonnetz verkar detta ackord vara det dubbla motstycket till ett dursjundeckord. Denna tolkning förstärks av observationen att detta G-skarpa mollackord med en tillagd lägre septim (E-skarp eller F är en septima under referensen för detta G-skarpa mollackord, D-skarpet) upplöses i ett E-durackord med en tillagd övre sjua (se även den intilliggande animerade figuren). Dessutom är Wagners sätt att sätta detta ackord kompatibelt med denna uppfattning, med tredje (B) och sjunde (F eller E-skarp) satta i ett lågt register. I Vogels notation skulle man notera detta ackord som 7Ud ♯ , eftersom referenstonen för det G-skarpa mollackordet är D-skarpet.
Det är inte särskilt troligt att Vogels notation för mollackord kommer att vinna erkännande. Det skulle kräva att ett C-molrackord betecknas som Ug, som lägre ackord under g. En kompromissnotation kan vara att beteckna Tristan-ackordet som G ♯ m/F, dvs som ett G-skarpt mollackord med ett F i basen.
"Förklaringen" av Tristan-ackordet i Vogels Tonnetz som ett välkomponerat motstycke till ett dur-sjundeackord kan inte jämföras med en "förklaring" inom ramen för funktionell harmoni. Båda typerna av förklaringar kan inte riktigt förklara varför vissa ackord och ackordsekvenser har etablerat sig i musikhistorien. Funktionell harmoni fokuserar på förhållandet mellan ett ackord och den rådande tonaliteten. Följaktligen kan den inte förklara ackordförlopp som finns i senromantisk musik där det inte längre finns en kontinuerlig tonalitet närvarande. Däremot fokuserar Vogels teori mer på överensstämmelsen mellan tonerna i ett enstaka ackord, eller med tonerna i det föregående eller efterföljande ackordet än på detta ackords roll i sammanhanget av en rådande tonalitet. Vogels analys avslöjar att Tristan-ackordet inte på något sätt är ett angrepp på tonsystemet som sådant utan att det är en del av det precis som dess motsvarighet, dursjundeackordet.
Ett liknande ackord används också ofta av jazzmusiker. Där noteras det vanligtvis som ett halvt förminskat septimackord. Tristan-ackordet kunde därför noteras som Fm 7 b5 ). Detta sätt att beskriva detta ackord missar dess relation till ett G-skarpt mollackord. Det är resultatet av övningen att beskriva ackord med början från deras lägsta ton. Enligt Vogel är detta lämpligt för övre ackord, men inte för lägre ackord. Nedre ackord ska beskrivas uppifrån och ner istället för nerifrån och upp. Principen att börja med den lägsta tonen iakttas följaktligen inte i andra situationer, till exempel med inverterade ackord . AC-durackord i sin första inversion beskrivs vanligtvis inte som ett e-mollackord med ändrad kvint (Em +5 ).
Reception
Vogels Tonnetz utgår från en teori (Eulers Tonnetz) som är mer än 100 år äldre än den för närvarande dominerande funktionella harmonin. Vogels Tonnetz och funktionell harmoni står inte i konflikt med varandra. Tvärtom kan de ses som att de kompletterar varandra: Medan Vogels teori fokuserar på lokala relationer mellan toner och ackord, betraktar funktionell harmoni den globala rollen av ett ackord i sammanhanget av hela musikstycket. Men förekomsten av funktionell harmoni och särdragen i Vogels notation hämmar det allmänna mottagandet. Vogels konsonansformel har först nyligen testats empiriskt. Kaernbach föreslår en förenklad notation: att alltid skriva från vänster till höger, använda versaler för referenstonerna (undvika förväxlingar med konventionen att använda gemener för mollackord) och använda en triangulär symbol (▲ och ▼) för att beteckna övre och nedre ackord. Början av förspelet till Tristan och Isolde kunde då betecknas som D ♯ ▼7 → E▲7.
Litteratur
- Martin Vogel: Der Tristanakkord und die Krise der modernen Harmonielehre. Düsseldorf 1962.
- Martin Vogel: Die Lehre von den Tonbeziehungen. Bonn 1976.
- Martin Vogel: Om tonens förhållande. Bonn 1993.