Visslornas fysik

En visselpipa är en anordning som gör ljud från forcerad luft. Den fysikaliska teorin om ljudframställningsprocessen är ett exempel på tillämpningen av vätskedynamik eller hydrodynamik . Genom att förstå visselpipans geometri, dimensioner och vätskeegenskaper kan man förutsäga dess egenskaper och hitta hydrostatisk jämvikt. De principer som är relevanta för visselpipedrift har även tillämpningar inom andra områden, såsom vätskeflödesmätning.

Typer

Wilson, et al., i sin studie av mänsklig vissling (se nedan), påpekade vikten av att inkludera symmetri eller asymmetri hos det instabila flödet utöver de återkopplingsklasser som anges nedan. På grund av det nära förhållandet mellan flödessymmetri och ljudfältet som genereras, inkluderades deras koncept här som en del av ljudkällans beskrivning (monopol – symmetrisk och dipol – asymmetrisk).

Monopol

Punktmonopol

Visslor som genererar ljud genom fluktuationer av massflöde över en gräns kallas monopolliknande källor. Figuren till höger är ett exempel på en liten sfär vars volym svänger. För denna typ av källa sänds ljudet ut radiellt, så ljudfältet är detsamma i alla riktningar och avtar med avståndets omvända kvadrat. Ljudstyrkan kan uttryckas som:

$W_{\text{m}}={\frac {\pi \rho _{0}}{c_{0}}}{\widehat {Q}}^{2}{\text{St}}^{2}U^{4}L^{2}$

Variablerna U och L anses vara karakteristiska för källan, och deras korrekta val är viktigt.

Dipol

Punkt dipol

Visslingar som genererar ljud genom fluktuationer av rörelsemängd eller stress och belastning av en kraft som utövas på det omgivande mediet kallas dipolliknande källor. Figuren till höger är ett exempel på en liten stel sfär som rör sig fram och tillbaka i en given riktning. Detta resulterar i ett ojämnt ljudfält. Ljudstyrkan kan uttryckas som:

$W_{\text{d}}={\frac {3\pi \rho _{0}}{c_{0}^{ 3}}}{\hat {F}}^{2}{\text{St}}^{2}U^{6}L^{2}$

Feedbackkategorier

Aerodynamiska visselpipor förlitar sig på instabiliteten i flöden och feedback som förstärker instabiliteten. Det finns flera sätt som feedback kan ske.

Kategori I

Ljudet från en visselpipa i denna kategori är i första hand en biprodukt av källrörelse. Ryggreaktionen är otillräcklig för att starkt kontrollera källans rörelse, därför är visselpipor inte i denna kategori.

Kategori II

Mediets bakreaktion är en avgörande faktor för källans rörelse. Instabil flytande rörelse eller ljudet som genereras av den kan återkoppla till källan och kontrollera den. Det som krävs är:

• en källa till stadig kraft;
• en förstärkningsmekanism som kan omvandla den konstanta effekten till tidsvarierande effekt;
• en störning, som tillhandahåller de svängningar som ska förstärkas;
• ett medel för att generera ljud eller annan oscillerande fluid Brownsk rörelse;
• ett medel för återkoppling av den oscillerande rörelsen som en störning av förstärkarens ingång.

Visslor är i denna kategori. Det finns flera sätt att beskriva feedbackprocessen.

Klass I

Återkopplingen är i huvudsak inkompressibel; ljudhastigheten, även om den är ändlig, är tillräckligt stor för att den kan anses vara oändlig. Denna åtgärd kan kallas hydrodynamisk återkoppling. Det finns ett antal klass I-enheter.

Klass II

Vissling feedback loop

Återkopplingen är komprimerbar och beror inte på ljudets hastighet. Denna åtgärd kan kallas kvasi-komprimerbar feedback.

Klass III

Återkopplingen är komprimerbar och beror på ljudets hastighet. Detta kan kallas akustisk återkoppling. Bilden till höger visar ett blockschema över dessa återkopplingsmekanismer. Alla aerodynamiska visselpipor fungerar under en av klasserna.

Etapper

Icke-linjära återkopplingsstadier

Feedback i visselpipor är olinjär mekanik eller kaos. På grund av olinjäriteten är det möjligt att ha mer än en frekvens vid en given flödeshastighet. Skillnaden beror på om flödet uppnås genom att öka flödet eller genom att minska flödet. Möjligheten för flera tillstånd kallas ett stadium och visas schematiskt i figuren till höger. När flödeshastigheten ökar ( Reynolds nummer , Re) klättrar frekvensen långsamt (nästan konstant Strouhal nummer , St) men sedan hoppar frekvensen upp abrupt till ett högre steg. När flödeshastigheten senare minskas minskar frekvensen långsamt men hoppar sedan abrupt ner till ett lägre steg. Detta mönster kallas en hysteresloop .

Högre stadier är förknippade med fler virvlar på det avståndet, vilket antyder att detta avstånd kan vara en viktig karaktäristisk dimension. I flera visslingar har tre stadier identifierats. Överblåsning i vissa blåsinstrument gör att steg I hoppar till steg II.

Flödesinstabilitet

Instabilitet hos laminära strålar

Instabil vattenstråle

Flödesinstabilitet är motorn för visselpipor. Den omvandlar stadig energi till tidsberoende energi.

Ett exempel visas i bilden till höger med en vattenstråle. Den laminära tvådimensionella strålen förstärker små störningar vid öppningen för att generera en virvelgata . För det här fallet ritades flödeshastigheten, i form av Reynolds-tal, mot störningsfrekvensen, i termer av Strouhal-talet för en mängd olika störamplituder för att avslöja området för instabilitet som visas i figuren till vänster. Värdet på D i figuren representerar förhållandet mellan den laterala störningsförskjutningen och munstyckets bredd; störningarna var små.

En viktig källa till instabilitet i en vätska är närvaron av en hastighetsgradient eller skjuvskikt med en brytpunkt. I en visselpipa börjar instabiliteten någon gång i den tredimensionella regionen och rör sig sedan längs någon väg i den regionen när de lokala variablerna ändras. Detta gör en heltäckande förståelse av instabilitetsmekanismer för visselpipor mycket svår.

Skalning

Visslor finns i alla former och storlekar, men deras funktion kan förenas genom begreppen dynamisk och geometrisk likhet med hjälp av dimensionsanalys . Naturen vet ingenting om de specifika mätsystem vi använder; den bryr sig bara om förhållanden mellan de olika krafterna, tidsskalorna och flera dimensioner. För att jämföra dem måste vi ta hänsyn till de etablerade förhållandena som är relevanta för visseldrift.

Likheten exponeras bäst genom att bestämma en hastighet U , det vill säga karakteristisk för dynamiken, och en dimension L , det vill säga karakteristisk för geometrin. Om dessa värden används i dimensionslösa siffror, som de som listas nedan, kan stor förståelse för fenomenet uppnås.

Strouhal nummer

Huvudartikel: Strouhal nummer

${\text{St}}={\frac {fL_{1}}{U}},\quad {\text{St}}_{ a}={\frac {fL_{2}}{c_{0}}}$

Den första siffran är förhållandet mellan instabila tröghetskrafter och stadiga tröghetskrafter. Numret namngavs för att hedra Vincenc Strouhal , som först härledde förhållandet mellan virvelavfallsfrekvensen runt en cylinder och flödeshastigheten. De karakteristiska variablerna var cylinderdiametern L ₁ och hastigheten U för flödet över den.

Detta antal gör det möjligt att utveckla relationer mellan de olika storlekarna och hastigheterna. Denna ekvation kan hänvisas till som ett fluidmekaniskt Strouhal-nummer i jämförelse med den andra versionen, som kan hänvisas till som det akustiska Strouhal-numret. Den första versionen används för den dynamiska likheten av den flytande rörelsen i visselpipor, medan den andra versionen används för den dynamiska likheten av den akustiska rörelsen i visselpipor. Många visselpipor kräver användning av båda siffrorna.

Mach nummer

Huvudartikel: Mach-tal

$M={\frac {U}{c_{0}}}$

Det är förhållandet mellan den konstanta hastigheten och ljudets hastighet . Numret döptes för att hedra Ernst Mach , som först studerade (bland annat) överljudsflöde och stötvågor. Detta nummer beskriver intervallet mellan flöden som kan anses vara inkompressibla och flöden som komprimerar

Reynolds nummer

Huvudartikel: Reynolds nummer

${\text{Re}}={\frac {UL}{\upsilon }}$

Det är förhållandet mellan de stadiga tröghetskrafterna och de stadiga viskösa krafterna . Numret namngavs för att hedra Osborne Reynolds , en ingenjör som gjorde banbrytande studier om övergången av laminärt till turbulent flöde i rör.

Rossby nummer

Huvudartikel: Rossby nummer

${\text{Ro}}={\frac {U}{f_{0}L}}$

Det är förhållandet mellan linjär hastighet och tangentiell hastighet för virvelflöden. Frekvensen är karakteristisk för flödets rotationshastighet. Numret namngavs för att hedra Carl-Gustaf Rossby , en meteorolog som först beskrev atmosfärens storskaliga rörelser i termer av vätskemekanik.

Dimensionslös kraft

${\hat {F}}={\frac {F}{\rho _{0}U^{2}L^{2}}}$

Förhållandet mellan den faktiska dynamiska kraften och den stadiga rörelsemängden och den jämna strömtätheten.

Dimensionslös volymetrisk flödeshastighet

${\hat {Q}}={\frac {Q}{UL^{2}}}$

Förhållandet mellan det dynamiska volymetriska flödet och det konstanta volymetriska flödet.

Monopolliknande visslingar

I dessa visslingar är flödesinstabiliteten symmetrisk, vilket ofta resulterar i periodiska ringvirvlar , och ljudgenereringen är associerad med fluktuationer i volymetriska/massflödeshastigheter.

Hålton (tekanna visselpipa, fågelrop)

Håltonsgeometri

Håltonsfrekvenser

Det jämna flödet från en cirkulär öppning kan omvandlas till ett oscillerande flöde genom att lägga till en nedströmsplatta med ett cirkulärt hål i linje med öppningen. Små störningar i flödet vid hålets återkoppling till öppningen orsakar en variabel volymetrisk flödeshastighet genom nedströmshålet på grund av återkopplingens symmetri. Störningen i strålen är en symmetrisk virvelring som rör sig med en viss hastighet långsammare än medelstrålehastigheten tills den träffar hålet, och en del vätska tvingas igenom det, vilket resulterar i ett monopolliknande ljudfält i halvrummet utanför. Bilden till höger visar schematiskt geometrin.

För att framkalla dynamisk likhet valdes den karakteristiska hastigheten i en studie till att vara medelhastigheten U för strålen vid mynningen och den karakteristiska längden valdes att vara mynningsdiametern δ . Tester gjordes på fem avstånd h / 5 från öppningen. Två skalningslagar användes: Strouhal-talet ritades som en funktion av Reynolds-talet. Resultaten visas i figuren till höger.

Frekvensen av tonen bestäms av hur ofta en virvel stötte på hålet medan den rörde sig med en hastighet u mindre än den ursprungliga jethastigheten. Eftersom strålen avtog när den fortsatte mot hålet, avtog virvelns hastighet med den, så frekvensen och Strouhal-talet var större på närmare avstånd. Strouhal-taldata visade tydligt det nästan linjära sambandet mellan frekvens och initial jethastighet. På fyra av de testade sträckorna var det hopp mellan etapp I och etapp II. Hystereslooparna är tydliga indikationer på den komplexa karaktären hos jetinstabilitetsförstärkningsstrukturen.

Likformigheten i det uppmätta ljudfältet för denna visselpipa bekräftade dess monopolliknande karaktär. Mätningar av hastighetsberoende för ljudnivån visade att den var mycket nära U ⁴ , vilket ytterligare bekräftar källans monopola natur. Vid dessa hastigheter och avstånd var återkopplingen normalt klass II, men reflekterande ytor så långt bort som 3 meter och med korrekt fasning styrde tonen och omvandlade återkopplingen till klass III.

Håltonen är också känd som tekannavisseln. De fann att över ett Reynolds-tal på 2000 inträffade håltonsoperation med symmetrisk virvelutveckling och ett konstant Strouhal-tal med Reynolds-tal. Vid lägre hastigheter svarade den cylindriska volymen som en Helmholtz-resonator . Baron Rayleigh var medveten om denna visselpipa; det kallades fågelkallet då. I Australien finns Tenterfield rävvisseln och den traditionella rävvisseln som verkar fungera som håltoner.

Korrugerad rör visselpipa

Huvudartikel: Whirly tube

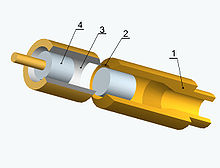
Korrugerad rör visselpipa

Denna visselpipa har dussintals populära namn. Rör med sinusformade radievariationer skapas ofta för att tillåta böjning. Stadigt flöde genom röret vid låga Reynolds-tal resulterar i en fluktuerande volymetrisk flödeshastighet som genererar ett monopolliknande ljudfält vid rörutgången. Exempel på sådana rör visas i figuren till höger.

Det gula plaströret är egentligen en barnleksak som låter när röret virvlas runt. Det visade metallröret användes i Concorde -cockpiten för att ge kylluft till piloterna, men dess höga ton fick det att avbrytas. Denna visselpipa liknar i många avseenden håltonen, i synnerhet tekannavisseln. Den är föremål för frekvenshopp och hysteresloopar. Det finns många artiklar på Internet om denna visselpipa, och den har studerats i akademisk litteratur.

Den karakteristiska hastigheten är medelflödet U genom röret och den karakteristiska längden måste vara en multipel av avståndet L mellan korrugeringarna, nL , där n är ett heltal. Vid låga hastigheter behöver det instabila inre flödet gå flera korrugeringar för att upprätta återkopplingsslingan. När hastigheten ökar kan slingan etableras med färre korrugeringar. Enkla tester utfördes på det gula plaströret.

Strouhal-numret

${\text{St}}={\frac {f_{n}nL}{U}}$

användes som skalningsfaktor. Den högsta frekvensen (7554 Hz) hittades i det "överblåsta" tillståndet, och n antogs vara en korrugering. Vid den lägsta flödeshastigheten jämfördes frekvensen 2452 Hz positivt med n = 3. Vid mellanflödeshastigheter inträffade flera icke-harmoniskt relaterade frekvenser samtidigt, vilket tyder på att flera korrugeringar var inblandade i ljudgenereringen. I det mindre metallröret uppträdde en dominerande ton vid 6174 Hz och motsvarade n = 2. En unik aspekt av denna visselpipa är att det interna flödet bär både den instabila virveln nedströms och den återkommande återkopplingssignalen uppströms.

Pipton (Pfeifenton)

En akustisk diod

Det unika med denna visselpipa är att tonen bara låter med flöde genom öppningen utifrån; det är en akustisk diod. En cylindrisk hålighet med ett litet cirkulärt, fyrkantigt hål i ena änden och helt öppet i den andra är känt för att generera en ton när luft passerar genom den. Den är föremål för frekvenshopp och hysteresloopar som liknar håltonen. Det verkar finnas två steg, och återkopplingen är sannolikt klass II om röret är kort. Grundtonen uppträder nära λ = 4 L , så en karakteristisk dimension är L , längden på röret. Den karakteristiska hastigheten U är hastigheten för flödet genom hålet.

Ett monopolliknande ljudfält genereras av volymetriska flödeshastighetsvängningar. Karthik och Anderson har studerat detta fenomen och kommit fram till att symmetrisk virvelavkastning på kavitetssidan är drivkraften.

Ett exempel på denna enhet visas i bilden till höger; den hade ett 0,125 tum (3,2 mm) diameter hål, var 1,9 tum (48 mm) långt och 0,8 tum (20 mm) i diameter. Kvartsvågsresonansen beräknades till 1780 Hz, medan den uppmätta grundtonen var 1625 Hz med detekterbara andra och tredje övertoner. Slutkorrigeringar för strålning från öppningarna behövs för att få de två frekvenserna i konsonans. För att bestämma ändkorrigeringarna behövs ytterligare två dimensioner: diametern d ₁ på öppningen och diametern d ₂ på röret.

Hartmann, Galton visslar (stamstråle)

Hartmann-visslan

Medan de tidigare visslingarna inträffar vid låga flödeshastigheter, inträffar denna vissling vid mycket höga hastigheter. När en subsonisk jet träffar en kavitet blir jet-instabilitet en del av återkopplingsslingan som med håltonen. När en överljudsstråle träffar en kavitet, blir akustisk stötvågsinstabilitet en del av återkopplingsslingan. Figuren till höger är ett exempel på denna visselpipa. En cylindrisk hålighet med ena änden öppen och vänd mot den supersoniska cirkulära strålen kommer att resultera i extremt intensivt ljud. Formerna i figuren representerar stöt-/expansionscellerna i strålen. En relaterad konfiguration, kallad stamstrålen , har en central stav i strålen som sträcker sig för att stödja och rikta in kaviteten. Det finns flera andra geometriska variationer, som alla fungerar på liknande sätt, till exempel ångvisseln .

Dessa enheter har studerats och granskats av Raman. Här tittar vi i första hand på Hartmann-visslan. Strålens stötceller samverkar med stöten framför kaviteten (flödet i kaviteten är subsoniskt). Små symmetriska störningar i jetströmmen förstärks när de fortsätter mot kaviteten (liknar i vissa avseenden håltonen), vilket gör att stöten framför kaviteten oscillerar. Stötfronten fungerar ungefär som en kolvkälla med hög energi, vilket resulterar i ett monopolliknande ljudfält. Återigen är det volymetriska flödet riktat, till skillnad från den teoretiska monopolen.

Ljudfältet kan likna det som skapas av oscillerande flöde från ett rör, förutom närvaron av överljudsstrålestrukturen, som kraftigt kan modifiera riktningen. Den ursprungliga ekvationen för Hartmann visas nedan:

${\begin{aligned}{\frac {\lambda }{ d}}&=5.8+2.5\left({\frac {h}{d}}-\left(1+0.0041(P-0.9)^{2}\right)\right)\\{\text{St }}&={\frac {fd}{c_{0}}}\approx 0,17\approx {\frac {fh}{U}}\end{aligned}}$

₀ Mynningens och kavitetens diameter är d , avståndet mellan mynningen och kaviteten är h , och mynningstrycket P angavs i kilogram kraft per kvadratmeter (1 kgf/m2 ^≈ 9,8 Pa). Vid den nedre gränsen för h försvinner den andra termen. I det här fallet kunde ekvationen ha formaterats om i termer av det akustiska Strouhal-numret, som visas i den andra ekvationen ovan. Den karakteristiska hastigheten U vid munstycket är ljudhastigheten c . Det är intressant att siffran ligger mycket nära det som Strouhal hittat för flöde över en cylinder. Det finns två karakteristiska längdskalor. Munstycksdiameter d kännetecknar ljudeffekten, medan separationsavståndet h kännetecknar frekvensen.

Omfattande studier av detta fenomen har visat att kavitetens position är avgörande för att skapa ljud. Processen har hysteresloopar, och frekvenserna är relaterade till multiplar av kvartsvåglängdsresonansen i kaviteten. Efter att ha formaterat om Hartmanns formel och använda den nya formuleringen ovan kan en ekvation för ljudstyrka skrivas som

${\begin{aligned}W_{h}&={\frac {\rho }{2}}{\frac {\pi d^{2}}{4}}(2\pi fa)^ {2}c_{0}\\&=A\rho f^{2}d^{2}h^{2}c_{0}\\&=A{\frac {\rho }{c_{0} }}\left({\frac {fd}{c_{0}}}\right)^{2}c_{0}^{4}a^{2}\\&=A{\frac {\rho _ {0}}{c_{0}}}{\text{St}}^{2}U^{4}L^{2}\end{aligned}}$

Galton-visslan

Eftersom den karakteristiska hastigheten U och ljudhastigheten i huvudsak är samma, kan den skrivas om som den andra ekvationen. Denna ekvation har samma struktur som den för punktmonopolen som visas ovan. Även om amplitudfaktorn A ersätter den dimensionslösa volymetriska flödeshastigheten i dessa ekvationer, bekräftar hastighetsberoendet starkt de monopolliknande egenskaperna hos Hartmann-visslan. En kusin till Hartmann-visseln visas i figuren till höger, Galton-visseln . Här exciteras kaviteten av en ringformig stråle , som oscillerar symmetriskt runt kavitetens skarpa kanter. Det verkar vara en cirkulär version av kanttonen (diskuteras nedan) där symmetrin hos kanttonens annars dipolkälla omvandlas till en monopolkälla.

Eftersom det är mycket troligt att svängningarna är koherenta runt periferin, bör det finnas en fluktuerande volymetrisk flödeshastighet från kaviteten med endast en liten nettokraft i sidled. Källan är alltså ännu en version av en monopolliknande geometri; den volymetriska flödeshastigheten är ett cylindriskt område mellan strålen och kaviteten.

Rijke-röret

Rijke-röret

Det finns flera visselfenomen där värme spelar en roll. Temperaturen i en ljudvåg varierar, men eftersom denna variation är så liten är det normalt vanligt att man försummar dess effekter. Men när förstärkning kan inträffa kan en liten variation växa fram och ha stor inverkan på ljudfältet som skapas. Den mest kända termiska visselpipan är Rijke-röret , ett vertikalt rör med ett uppvärmt gasvävsmaterial placerat inuti.

₀₀ Ursprungligen värmdes gasväven med en bunsenbrännare; senare värmdes ett trådnät elektriskt. Värmen som överförs till luften i röret sätter den i nästan halvvågsresonans om gasväven placeras under rörets mittpunkt som visas i figuren till höger. Det finns inget teoretiskt optimalt läge, eftersom våghastigheten uppåt är c ​​+ u , konvektionshastigheten, medan våghastigheten nedåt är c ​​− u . Utan konvektionsflöde är mittpunkten och den nedre röränden de bästa platserna för värmeöverföring. Med konvektion väljs normalt ett kompromissläge halvvägs mellan de två punkterna, vilket beror på mängden tillförd värme. En karakteristisk längd förknippad med frekvens är rörlängden L .

En annan karakteristisk längd förknippad med ljudstyrka är αL , gasvävens position. Den karakteristiska hastigheten måste vara konvektionshastigheten u vid värmekällan. För detaljerad studie av visselpipan, se Matveev. Eftersom den första modens resonans är ungefär halvvåg, kommer ljudfältet som emitteras från röret från två i-fas monopolliknande källor, en i vardera änden. En gaslåga inuti ett rör kan driva resonans; det kallades en sjungande låga . Det finns ett omvänt Rijke-rör, där varm luft passerar genom ett kallt galler.

Sondhauss och Taconis tuber

Sondhauss-röret är en av de tidiga termiska tongeneratorerna; det upptäcktes i glasblåsningsindustrin. En glödlampa med varmluft är ansluten till ena änden av ett rör som har rumstemperatur. När det kalla röret blåser uppstår akustiska rörsvängningar. Det diskuterades av Baron Rayleigh i hans "Theory of Sound". Denna enhet anses inte vara en sann visselpipa, eftersom svängningarna avtar när temperaturerna utjämnas.

Vid analysen av detta rör noterade Rayleigh att om värme hade tillförts vid punkten med högsta densitet i ljudvågen och subtraherad vid punkten med lägst densitet, skulle vibrationen uppmuntras. En annan termisk effekt kallas Taconis-oscillationen. Om ett rör av rostfritt stål har en sida i rumstemperatur och den andra sidan i kontakt med flytande helium och superfluid helium, observeras spontana akustiska svängningar. Återigen, Sondhauss-röret är inte en riktig visselpipa.

Mänsklig visselpipa

Huvudartikel: Visslande

Mänskligt visselljud

Antalet och variationen av visselpipor som skapas av människor är ganska stora, men ändå har väldigt lite gjorts för att undersöka processens fysik. Det finns tre möjliga mekanismer: Helmholtz-resonans , symmetrisk håltonoperation (monopol) eller asymmetrisk kanttonsoperation (dipol).

Wilson och hans kollegor har simulerat den mänskliga visselpipan genom att skapa en cylinder 2,04 tum (52 ​​mm) i diameter med en rundad öppning i ena änden som försörjde en stråle och en annan rundad öppning i den andra änden av samma diameter och på samma axel. Geometrin var mycket lik den för tekannas visselpipa. Efter ett antal tester med olika hastigheter, öppningsdiametrar och öppningstjocklekar kom de fram till att visselpipan skapades av en Helmholtz-resonans i cylindervolymen. Det fanns tillräckligt med data för ett fall i deras studie för att beräkna Strouhal- och Reynolds-talen. Resultaten visas i figuren till höger.

Strouhal-talet var i huvudsak konstant över det begränsade hastighetsintervallet, vilket tyder på håltonsdrift med klass I eller klass II återkoppling. Deras arbete indikerade symmetriskt instabilt virvelflöde, som man kunde förvänta sig, men det nämndes inget om stadier. I studien av Henry Wood, noterades det att Helmholtz-resonans kunde uppstå vid Munnens flexibilitet tyder på att även om en återkopplingsmekanism i hålton är högst sannolik, anses möjligheten för Helmholtz-resonanser i munhålan och asymmetriska kanttonseffekter med tänderna vara möjliga.

Lövvissling

Bladet kan användas som en visselpipa som kan producera upp till tre oktaver. Det är ett populärt instrument i många kulturer, kallas slek i Kambodja, 木叶 (Mù yè) i Kina, gummiblad i Australien och Birkenblatt Blasen i Tyskland. Genom att använda en höghastighetskamera kan man se att bladet rör sig bort från läpparna när spelaren blåser och dess elasticitet för det tillbaka till läppen, denna oscillerande rörelse sätter det i vibration för att producera ett ljud. En analys av övertonsserien som jämför en oboe och birkenblatt som spelar noten F2 visar att de är nästan identiska.

Dipolliknande visslingar

I dessa visselpipor är flödesinstabiliteten asymmetrisk, vilket ofta resulterar i rader av alternerande virvlar, och ljudgenereringen är förknippad med fluktuationer av applicerad kraft. Ljudfältet är så nära en dipolkälla som lokal geometri tillåter.

Eolisk ton

Cylinder virvelgata

Eolisk ton

Det jämna flödet över en cylinder (eller liknande föremål) genererar virvelavfall och därav följande ljud. De tidiga grekerna använde detta fenomen för att utveckla en harpa, och ljudet kallades en eolisk ton efter Aeolus , vindens gud.

Visslande telefonkablar, bilradioantenner, vissa frontgaller för bilar och rökstaplar är andra exempel på denna ton. Vid mycket låga Reynolds-tal är flödet runt en cylinder stabilt och bildar två fasta virvlar bakom den. När hastigheten ökar blir flödet, även om det är laminärt, instabilt och virvlar avges växelvis .

Hydrodynamisk återkoppling (klass I) påverkar bildandet av nya virvlar och utövar en fluktuerande kraft på cylindern. Flödesfältet visas i den övre figuren till höger (skapat av Gary Koopman). Theodor von Karman identifierade och analyserade flödet bakom föremål som en cylinder, och sedan dess har detta speciella flöde kallats Karman-virvelgatan . Vincenc Strouhal var den första som vetenskapligt undersökte ljudet som avges av flödet runt en stel cylinder. Vid låga Reynolds-tal var tonen ren, och frekvensen var proportionell mot den konstanta flödeshastigheten U och omvänt proportionell mot cylinderdiametern d .

För många tillämpningar används ofta den första ekvationen nedan. En genomgång av litteraturen tog fram figuren till höger för Strouhal-numret. Vid låga Reynolds-tal stiger Strouhal-talet när tröghetseffekter börjar dominera och avtar sedan något vid högre tal. Den andra ekvationen nedan passar bäst för data för 1000 < Re < 100 000 .

${\begin{aligned}{\text{St}}&={\frac {fd}{U}}\approx 0.2;\\{\text{St}} &=0.218\left({\frac {\text{Re}}{1000}}\right)^{-0.042}\end{aligned}}$

Cylindervirvelutveckling

Det är förvånande hur ofta oscillerande flödesfenomen har Strouhal-tal i detta intervall. För formjämförelse har Strouhal-talet för en ellips uppmätts till 0,218, en cylinder till 0,188, en kvadrat till 0,160 och en triangel till 0,214. Den karakteristiska dimensionen är den för objektet lateralt mot flödet och den karakteristiska hastigheten är den för det infallande flödet.

Den andra ekvationen antyder att Strouhal-talet är en svag negativ funktion av Reynolds-talet. Detta tyder på att den dynamiska likhetsapproximationen är rimlig. Den fluktuerande kraften som utövas på cylindern är ett resultat av flödescirkulationen runt den orsakad av den alternerande virvelseparationen som föreslås i den tredje figuren. Det faktum att virvlarna inte är direkt bakom cylindern antyder att kraftvektorn har både en lyft- och dragkomponent, vilket resulterar i lyft- och dragdipoler.

Ett ungefärligt sätt att relatera ljudet som genereras till flödesegenskaperna är att störa standardmotståndsekvationen med hastighetsstörningar som visas i den övre ekvationen nedan (lyftmätningar för cylindrar är i allmänhet inte tillgängliga). Den övre ekvationen är den modifierade motståndsekvationen med både motståndskomponenten u och lyftkomponenten v och tvärsnittsarean dL , där d är cylinderdiametern och w är längden.

${\begin{aligned}F&=F_{d}+F'_{d}+ F'_{l}={\frac {C_{d}\rho _{0}}{2}}(U+u'+v')^{2}\,dw\\W_{d}&= {\frac {3\pi \rho _{0}}{c_{0}^{3}}}S^{2}U^{6}dwC_{d}^{2}{\overline {\left( {\frac {u'}{U}}\right)^{2}}}\\W_{l}&={\frac {3\pi \rho _{0}}{c_{0}^{3 }}}S^{2}U^{6}dwC_{d}^{2}{\overline {\left({\frac {v'}{U}}\right)^{2}}}\end {Justerat}}$

Eolisk ton

Manipulering av ekvationen ger de två nedre ekvationerna för dipolljudstyrkan för både lyft och motstånd. Varje gång en virvel släpps ut har luftmotståndshastighetsfluktuationen u samma tecken, men sidohastighetsfluktuationen v har motsatta tecken, eftersom virveln avges på alternerande sidor. Som ett resultat skulle dragdipolen förväntas ha dubbelt så hög frekvens som lyftdipolen.

Phillips fann att laterala hastighetsfluktuationer var två storleksordningar större än den longitudinella, så lyftdipolen är 20 dB över dragdipolen. Han fann att dragdipolen inträffade vid dubbelt så hög frekvens som lyftdipolen. Vid högre hastigheter kan det hända att virvelseparationen inte är korrelerad över cylinderns hela längd, vilket resulterar i flera väsentligen oberoende dipolkällor och lägre ljudeffekt. Den nedre figuren till höger visar korrelationskoefficienten som funktion av avståndet längs cylindern och är från Etkin, et al. studie.

Slutande ton

Glider ljud

Bakkantton

Bakkantsspektra

Gränsskiktet på ett segelflygplans aerodynamiska yta är laminärt, och virvelavkastning som liknar den hos en cylinder inträffar vid bakkanten. Ljudet kan vara en nästan ren ton.

Figuren till vänster visar ett en tredjedels oktavbandsspektrum taget under ett segelflygplan; tonen är 15 dB över bredbandsljudet. Flygplanets hastighet U var 51 m/s (170 ft/s), och frekvensen var nära 1400 Hz.

, beräknades den karakteristiska dimensionen δ till nära 0,25 tum (6,4 mm); gränsskiktets tjocklek. Ett dipolljudfält skapades vid bakkanten på grund av den fluktuerande kraften som utövades på den.

Vid högre hastigheter på motordrivna flygplan är gränsskiktet på bärytan turbulent, och mer komplexa virvelavfallsmönster har observerats. Eftersom det är svårt att mäta under flygning gjorde Hayden statiska tester.

Bilden till höger visar ett exempel. Ett gränsskiktsflöde skapades på båda sidor av en tunn stel platt platta som avslutades med en fyrkantig bakkant. Notera den nästan rena tonen vid 2000 Hz med ett Strouhal-tal på 0,21 som sticker ut över det turbulenta ljudspektrumet. Återigen dyker Strouhals magiska nummer upp. Den karakteristiska hastigheten var medelhastigheten U för strålen, och den karakteristiska dimensionen valdes som bakkantstjockleken t . Den bättre karakteristiska dimensionen hade varit gränsskiktets tjocklek, men lyckligtvis var de två dimensionerna nästan lika. Det uppmätta ljudfältet var tydligt dipolliknande (modifierat något av plattans närvaro).

Den nedre figuren till höger visar ett antal turbulenta ljudspektra uppmätt i olika hastigheter. Frekvenserna var Strouhal-nummer skalade med U , och ljudnivåerna skalades med dipolljudeffektregeln U ⁶ över ett hastighetsområde på 3 till 1. Datapassningen var ganska bra, vilket bekräftar dynamisk likhet och dipolmodellen. Den lilla skillnaden i nivå och frekvensöverlappning tyder på att både den dimensionslösa kraften och Strouhal-talet var svagt beroende av Reynolds-talet.

En annan karakteristisk dimension är aerofoil-ackordet. I dessa tester var strålens bredd tillräcklig för att hålla virvelavkastningen koherent över den. På en bäryta skulle det finnas en korrelationslängd som är mindre än vingspannet, vilket resulterar i flera oberoende dipoler anordnade i sidled. Ljudeffekten skulle minska något. Eftersom dipolmodellen är baserad på tidshastigheten för förändring av kraften, kan en minskning av ljudeffekten åstadkommas genom att minska den hastigheten. Ett möjligt sätt skulle vara att de motsatta sidorna av ytan gradvis avkänner varandra spatialt före bakkanten och sålunda minska hastigheten vid kanten. Detta kan göras av en sektion av graderade porösa eller flexibla material.

Cirkelsågsvissling

En del av sågbladet

En kantton uppstår när en stråle träffar en fast yta. En bakkantton uppstår när ett yttre flöde passerar över en bakkant. Det finns en visselpipa som är en kombination av en kantton och en bakkantston och kan kallas en wake-edge-ton . Det förekommer i roterande cirkelsågar under tomgång och kan kallas för cirkelsågsvisseln . Under belastningsförhållanden spelar bladvibrationer en roll, vilket inte tas upp här.

Det har gjorts flera studier av de grundläggande ljudgenererande mekanismerna för denna visselpipa.

En ritning av typisk bladkonstruktion visas i bilden till höger. Forskning har visat att ljudfältet är dipol med primäraxeln vinkelrät mot bladplanet. Källorna är fluktuerande krafter som verkar på varje skärblad. Bies bestämde att den karakteristiska hastigheten var bladhastigheten RΩ , och den karakteristiska dimensionen var tandarean. Andra forskare använde bladtjocklek som den karakteristiska dimensionen. Cho och Mote fann att Strouhal-talet St = fh / U var mellan 0,1 och 0,2, där h var bladets tjocklek. Poblete et al., fann Strouhal-tal mellan 0,12 och 0,18. Om kanttonen är relevant bör kanske den karakteristiska dimensionen vara gapet mellan bladen.

Forskarna drog slutsatsen att den fluktuerande kraften var proportionell mot U ² , men ljudeffekten visade sig variera från U ^4,5 till U ^6,0 . Om mätbandbredden är bred och mätavståndet är utanför närfältet, finns det två dynamiska faktorer (Strouhal-tal och dimensionslös kraft), som kan göra att exponenten är mindre än 6. Både deltametern och håltonsdata visar Strouhal tal är en svag negativ funktion av Reynolds tal, som kvadreras i ljudeffektekvationen. Detta skulle resultera i en reducerad hastighetsexponent. Denna faktor förklarar dock inte den stora minskningen i exponent.

Bladgeometrin var mycket varierande i testerna, så det är troligt att det negativa beroendet av den dimensionslösa kraften på Reynolds nummer är huvudfaktorn. Denna visselpipa har två funktioner som skiljer den från de andra visslingarna som beskrivs här. Den första är att det finns en mångfald av dessa dipolkällor arrangerade runt periferin, som med största sannolikhet strålar ut med samma frekvens, men osammanhängande. Den andra är att bladrörelsen skapar ett stadigt men roterande tryckfält vid varje blad. Den roterande stabila kraften skapar ett roterande dipolfält, som har inflytande i det geometriska närfältet. Återkopplingen är klass I (hydrodynamisk), och det finns ingen indikation på att andra steg än steg 1 inträffar.

Ringsignal

Ringflödesfält

Ringljud

Ordet "ring" syftar här på formen och inte på klockljudet. Flödet från en cirkulär öppning som träffar en toroidformad ring med samma diameter som öppningen kommer att resultera i en ton; det kallas ringsignal . Den liknar håltonen som beskrivits ovan, förutom att eftersom plattan ersatts av en ring, uppstår en fundamental förändring i det resulterande ljudfältet. Små störningar vid ringen matas tillbaka till öppningen för att förstärkas av flödesinstabiliteten (klass I). Det instabila flödet skapar en uppsättning symmetriska (ring) virvlar som senare träffar den fysiska ringen.

En virvels passage genom ringen visas schematiskt i figuren till höger i tre steg. Flödesvektorerna i figuren antyder endast riktning.

När två virvlar är lika långt från ringen, den ena är bortom och den andra närmar sig, är nettocirkulationen runt ringen noll; nollpunkten för flödesoscillationen. Varje virvel skapar ett cirkulärt (ring) flödesfält vars axel varierar något från vertikalen när den passerar. Figuren antyder att huvudkomponenten av kraften på den fysiska ringen är i riktning mot jetflödet. Om virveln är en sann ring (alla delar är i fas) skapas ett dipolljudfält riktat längs jetaxeln.

Figuren antyder också att det finns en lateral kraftkomponent, som bara kan tolkas som en svag radiell dipol. Experiment har utförts på ringsignalen. Den nedre figuren till höger visar förhållandet mellan frekvens och Reynolds tal. Om Strouhal-talet plottats istället för frekvensen, skulle det ha visat att konturerna var någorlunda konstanta liknande konturerna för håltonen. Närmare granskning av data i figuren visade ett litet negativt beroende av Strouhals nummer på Reynolds nummer.

Det verkar som om denna visselpipa bara har två steg. Ljudfältet mättes och indikerade tydligt en dipol, vars axel var i linje med jetaxeln. Eftersom det inte fanns några reflekterande ytor nära källan, indikerade data också att en svagare radiell dipolkomponent också existerade. Ett sådant fält kan endast existera om det finns en tidsfördröjning vid en avlägsen punkt mellan var och en av kraftkomponenterna.

==

Vortex visselpipa

Vortexvisseln

Vortex-visselfrekvenser

När det virvlande flödet i ett rör möter utgången kan det bli instabilt. Ett exempel på originalsystemet visas i bilden till vänster. Instabiliteten uppstår när det är ett omvänt flöde på axeln.

Själva rotationsaxeln precesserar runt röraxeln, vilket resulterar i en roterande kraft vid rörutgången och resulterar i ett roterande dipolljudfält. Studier av denna visselpipa har visat att dynamisk likhet baserad på rördiametern d som den karakteristiska längdskalan och inloppets medelflödeshastighet U som den karakteristiska hastigheten inte uppnåddes, som visas i den nedre bilden till höger. En mer korrekt hastighet skulle vara den karakteristiska för virveln fd , där f är precession (och ljud) frekvensen, baserat på Rossby-talet . För att testa relevansen av denna nya karakteristiska hastighet ökades flödeshastigheten och ljudets frekvens och nivå mättes. Med hjälp av dipolmodellen visade sig den beräknade kraften vara nästan proportionell mot ( fd ) ² , vilket bekräftar riktigheten av den nya karakteristiska hastigheten.

Mätningar visade att virvelvisseln skapades av en roterande asymmetrisk virvel, som skapade en roterande kraftvektor i utgångsplanet och ett roterande dipolljudfält. Fenomenet med virvelinstabilitet har visat sig förekomma i andra situationer. Den ena var flödesseparationen på ovansidan av deltaformade bärytor på höghastighetsflygplan ( Concorde ). Framkantens anfallsvinkel resulterade i ett virvelflöde som blev instabilt. En annan är flödet i cyklonseparatorer; det virvlande flödet där sker i ett ringformigt område mellan två rör. Flödet vänder vid den slutna änden av det yttre röret och går ut genom det inre röret. Under vissa förhållanden blir flödet i reverseringsområdet instabilt, vilket resulterar i en periodisk roterande kraft på ytterröret.

Periodiska vibrationer av en cyklonseparator skulle indikera virvelinstabilitet. Stora centrifugalfläktar använder ibland radiella inloppsblad som kan roteras för att kontrollera flödet in i fläkten; de skapar ett virvlande flöde. Vid nästan avstängning, där virveln är mycket hög, roterande bladstopp av fläktbladen. Även om det inte undersökts, är det mycket troligt att virvelinstabilitet är orsaken. Återkopplingen är klart hydrodynamisk (klass I), och det finns inget som tyder på att mer än ett steg inträffar.

Virvelmätare

Flödesmätare

Metoden att skapa virvel i virvelvisseln ansågs vara orsaken till bristen på dynamisk likhet, så virveln skapades i ett rör med en sammandragning med virvelblad följt av en expansion för att skapa det erforderliga axiella tillbakaflödet. Detta var virvelvisseln i ett rör. Mätningar gjorda med denna geometri visas i figuren till höger. Som kan ses uppnåddes dynamisk likhet med både luft och vatten. Denna visselpipa blev en flödesmätare som kallas virvelmätaren . Dess noggrannhet kan jämföras med de virvelavskiljande mätarna som beskrivs ovan, men har ett högre tryckfall. Återkopplingen är hydrodynamisk (klass I), och endast ett steg hittades.

Kantton

Kanttonsvirvlar

Kanttons dipolliknande flöde

Wake-edge ton

När en rektangulär stråle träffar ett föremål med vassa kanter, såsom en kil, kan en återkopplingsslinga upprättas, vilket resulterar i en nästan ren ton. Figuren till höger visar schematiskt cirkulationen av två virvlar när de passerar kilen. Detta enkla diagram antyder att det finns en kraft som appliceras på kilen, vars vinkel varierar när virvlarna passerar.

Som man finner i den eoliska tonen är den vertikala komponenten (lyften) stor och resulterar i ett dipolliknande ljudfält vid kilen (visas i den nedre figuren) och en mycket svagare horisontell komponent (drag) vid dubbelt så hög frekvens (visas ej). ). Dragkomponenten kan bidra som en del av drivkraften för musikinstrument (diskuteras nedan). En framträdande studie av Powell av detta fenomen har avslöjat många detaljer om kanttonsfenomenet. Han visade att denna visselpipa har tre steg, och återkopplingsslingan var hydrodynamisk (klass I). En semi-empirisk ekvation för frekvensen, utvecklad av Curle, när den konverteras till Strouhal tal, är

${\text{St}}_{n}={\frac {fh}{U}}=\left({\frac {4n+1}{8}}-{\frac {h}{60d }}\höger).$

Denna ekvation, tillämplig för h / d > 10, visar medelhastigheten U för strålen vid mynningen som karakteristisk hastighet och avståndet h från mynningen till kanten som den karakteristiska dimensionen. Heltalet n representerar de olika virvellägena. Det tyder också på att dynamisk likhet uppnås till en första approximation; en avvikelse är att hastigheten vid kilen, som är mindre än den vid mynningen, ska vara den karakteristiska hastigheten. En svag negativ Reynolds-taleffekt är trolig. Mynningens bredd d har också viss inverkan; det är relaterat till virvelstorleken och den laterala korrelationen av avskiljningsprocessen.

Närvaron av ett dipolljudfält och en periodisk kraft proportionell mot U ² bekräftades av Powell. Numeriska simuleringar av kanttonen och omfattande referenser finns i en NASA-rapport. Den nedre siffran till höger kan kallas en wake-edge-ton . Om de föredragna frekvenserna för bakkantsinstabiliteten matchar de föredragna frekvenserna för den fria kanttonen, bör ett starkare dipolljud uppstå. Det verkar inte finnas någon forskning om denna konfiguration.

Ton med grund hålighet

Studiet av ljud som genereras av flöde över kaviteter i hög hastighet har finansierats väl av den federala regeringen, så en stor ansträngning har gjorts. Problemet hänför sig till flöde över flygplanskaviteter under flygning såsom bombrum eller hjulbrunnar. Flöde över en kavitet i en yta kan resultera i excitation av en återkopplingsslinga och nästan rena toner. Till skillnad från kanttonen som noterats ovan är kavitetskanten typiskt fyrkantig, men kan också vara en kant som en del av ett tunt strukturellt skal. Kaviteter kan separeras i grunda eller djupa , skillnaden är att för djupa kaviteter kan en klass III (akustisk) återkopplingsväg vara styrande. Grunda kaviteter tas upp här och är de där kavitetslängden L är större än kavitetsdjupet D .

Vid höga hastigheter U är flödet turbulent, och i vissa studier kan hastigheten vara överljud, och den genererade ljudnivån kan vara ganska hög. En studie har visat att flera oscillationssätt (stadier) kan förekomma i en grund hålighet; lägena är relaterade till antalet virvlar i avståndet L . För kortare kaviteter och lägre Mach-tal finns det ett skjuvlagerläge , medan det för längre kaviteter och högre Machtal finns ett wake-läge . Skjuvskiktsläget kännetecknas väl av feedbackprocessen som beskrivs av Rossiter. Wake-läget kännetecknas istället av en storskalig virvelavkastning med ett Strouhal-tal oberoende av Mach-tal. Det finns en empirisk ekvation för dessa data; det kallas Rossiters formel .

Lee och andra har visat den i Strouhal nummerform som

${\text{St}}_{n}={\frac {f_{n}L}{U}}= {\frac {n-\beta }{U\left({\frac {1}{c_{0}}}+{\frac {1}{u_{v}}}\right)}}$

₀ Termen inom parentes inkluderar två återkopplingshastigheter: nedströmshastigheten är hastigheten för virvlarna u , och uppströmshastigheten är ljudets c . De olika moderna beskrivs av ett heltal n med en empirisk fördröjningskonstant β (nära 0,25). Heltalet n är nära relaterat till antalet virvlar på väg till kanten. Det är tydligt från skuggbilder att den fluktuerande kraften nära nedströmskanten är ljudkällan. Eftersom flödets Mach-tal kan vara avsevärt gör brytning det svårt att bestämma huvudaxeln för det dipolliknande ljudfältet. De föredragna frekvenserna i grunda kaviteter skiljer sig från de för kanttonen.

Polisen visslar

Polisvisslande operation

Det används ofta för att beskriva visselpipor som liknar dem som används av polisen i Amerika och på andra håll. Det finns ett antal visselpipor som fungerar på samma sätt som polisen visselpipor, och det finns ett antal visselpipor som används av polisen på andra håll som inte fungerar på samma sätt som polisen. London Metropolitan-polisen använder en linjär visselpipa, mer som en liten brännare. Polisvisslar används ofta av domare och domare i sportevenemang.

Tvärsnittet av en vanlig visselpipa visas i bilden till höger. Kaviteten är en cylinder med sluten ände ( 3 ⁄ 4 tum (19 mm) diameter), men med cylinderaxeln lateralt mot jetaxeln. Mynningen är mm . 1,6 mm 6,4 från bred och den skarpa kanten är jetmunstycket När det blåser svagt är ljudet mestadels bredband, med en svag ton. När den blåser kraftigare skapas en stark ton nära 2800 Hz, och närliggande band är minst 20 dB nere. Om visselpipan blåser ännu kraftigare ökar tonens nivå och frekvensen ökar endast något, vilket tyder på hydrodynamisk återkoppling av klass I och drift endast i steg I.

Det verkar inte finnas någon detaljerad forskning om polisens visselpipa. Med tanke på kanttonen, noterad ovan, kan man förvänta sig flera hopp i frekvens, men inga inträffar. Detta tyder på att om det finns flera virvlar i den instabila jetstrålen så kontrollerar de inte.

Diagrammet till höger föreslår en rimlig förklaring av visselpipans funktion. Inuti kaviteten finns en virvel utanför mitten. I den övre ritningen är virvelcentrum nära strålen; det närliggande kavitetsflödet är långsammare och trycket är lägre än atmosfärstrycket, så strålen riktas in i kaviteten. När strålen rör sig mot kaviteten, ges en extra dragkraft till det inre vertikala flödet, som sedan roterar runt och tillbaka till kanten. Vid den punkten är kavitetsflödet och det lokala trycket tillräckligt för att tvinga strålen att röra sig bort från kaviteten.

En inre virvel av denna typ skulle förklara varför inga frekvenshopp inträffar. Eftersom överskottsvätskan i kaviteten måste släppas ut, måste strålens sidorörelse vara avsevärt större än den som finns i kanttonen; detta är troligen orsaken till det höga ljudet. Flödet över kanten resulterar i en applicerad kraft och ett dipolliknande ljudfält. Den karakteristiska hastigheten måste vara jetutgångshastigheten U . Det karakteristiska måttet måste vara kavitetsdiametern D .

Ljudets frekvens är nära relaterad till rotationshastigheten för kavitetsvirveln. Med en frekvens nära 2800 Hz måste den inre rotationshastigheten vara mycket hög. Det är troligt att Rossby-talet U /( fD ) skulle vara ett värdefullt dynamiskt likhetstal. Båtsmansröret liknar polisens visselpipa, förutom att hålrummet är sfäriskt, vilket skapar en mer komplex virvel .

Ärtvisslinga/domarens visselpipa

En ärtvisslinga är konstruktionsmässigt identisk med en "polisvisslinga", men kammaren innehåller en liten boll, känd som ärtan, men vanligtvis ett material som plast eller hårdgummi. När den blåses rör sig ärtan kaotiskt i kammaren, vilket avbryter och modulerar luftflödet för att skapa en typisk vrål/skrikeffekt. Sådana visselpipor används traditionellt av förbundets fotbollsdomare och domare i andra spel.

Samba visslar

I likhet med ärtvisslor har sambavisslor en liten kula eller plugg för att skapa samma sorts ljud, men har ofta också två förlängningar på vardera sidan av kammaren. Ingen, en eller båda av dessa kan blockeras för att skapa en "tri-tone" effekt. Apito de samba är ett traditionellt portugisiskt exempel på en sambavissla.

Levavasseur visselpipa

Levavasseur visselpipa

Denna visselpipa är i huvudsak polisvisseln som förvandlats till en torus, som förstärker dess ljudskapande potential. Ett tvärsnitt genom mitten av visselpipan visas i bilden till höger.

En ringformad kanal bär vätskan som skapar den ringformade strålen. Strålen träffar en ring med vass ände med två toroidformade håligheter på vardera sidan. I Levavasseurs patent läggs en struktur nedströms den ringformade öppningen för att fungera som ett kopplingshorn för att styra ljudet. Ljudet som genereras är väldigt intensivt. Det verkar som om ingen vetenskaplig studie har gjorts för att klargöra de detaljerade återkopplingsmekanismerna för dess funktion, även om det är tydligt att denna visselpipa har klass I återkopplingsmekanism, liknande polisvisseln.

Den karakteristiska hastigheten U är den för den ringformade strålen. Den karakteristiska dimensionen D är kavitetsdiametern och det verkar som om båda kaviteterna har liknande dimensioner. Återigen, Rossby-numret VU /( fD ) är sannolikt ett relevant dynamiskt tal, eftersom funktionen av den inre kaviteten måste likna den i polisens visselpipa. Det är troligt att virveln i den yttre kaviteten är i motfas med den inre kaviteten för att förstärka jetförskjutningen och därmed ljudet.

Skrik ton

Starka toner kan uppstå i både rektangulära och cirkulära strålar när tryckförhållandet är större än det kritiska och flödet blir överljud vid utträde, vilket resulterar i en sekvens av repetitiva stötceller. Dessa celler kan ses i avgaserna från raketer eller jetplan som arbetar med en efterbrännare. Precis som med subsoniska jetstrålar kan dessa flöden vara instabila.

I en rektangulär stråle kan instabiliteten visa sig som asymmetriska cellförvrängningar. Asymmetrin skickar vågor tillbaka till munstycket, vilket sätter upp en klass III återkopplingsslinga och ett starkt periodiskt dipolljudfält; det kallas skrikton . Powell beskrev först fenomenet och på grund av tillämpning på militära flygplan och potentiell strukturell trötthet har mycket efterföljande arbete gjorts. Ljudfältet är tillräckligt intensivt för att det ska synas på en skugggraf som visas i bilden till höger (från MG Davies ) för en rektangulär överljudsstråle. Källans dipolkaraktär är tydlig genom fasomkastningen på vardera sidan av strålen. Det finns en sidorörelse av stötcellerna som ger dipolen dess axel.

Överljudsflöden kan vara ganska komplicerade, och några preliminära förklaringar finns tillgängliga. Precis som med hål och ringsignaler kan dessa strålar vara känsliga för lokala ljudreflekterande ytor.

Den karakteristiska hastigheten U är den i utgångsplanet, och den karakteristiska dimensionen L är munstycksbredden, mot vilken celldimensionerna är proportionella. Cirkulära överljudsstrålar genererar också skriktoner. I det här fallet kan det dock finnas tre rörelsesätt : symmetrisk (toroidal), asymmetrisk (sinuus) och spiralformad. Dessa visselpipor skiljer sig från de andra som anges ovan; ljudet genereras utan interaktion med ett fast ämne; det är verkligen en aerodynamisk visselpipa.

Fluidiska oscillatorer

Vätskeanordning

Strouhal nummer

Strouhal nummer

Dessa enheter är visselpipor som inte utstrålar ljud, men är fortfarande aerodynamiska visselpipor. Den övre bilden till höger visar grundarrangemanget för en version av enheten. Cirkeln till vänster är vätskekällan (luft eller vätska). En stråle bildas som antingen går in i den övre eller nedre kanalen.

De svarta linjerna är återkopplingsvägarna. Om vätskan finns i den nedre kanalen, matas en del vätska tillbaka till strålens ursprung genom det svarta röret och skjuter strålen till den övre kanalen.

Det har skett en betydande utveckling av dessa enheter från kretsomkopplare som är immuna mot elektromagnetiska pulser till mer modern användning.

En unikhet med denna visselpipa jämfört med de andra beskrivna är att längden på återkopplingsvägen kan väljas godtyckligt. Även om kanalerna är uppdelade av en kilform, undviks kanttonsoperation av Coandă-effekten . Den andra figuren till höger visar resultat från en studie som indikerar ett konstant Strouhal-tal med Reynolds-nummer. Uppgifterna hade normaliserats till ett referensvärde.

I en annan studie räknades en uppsättning av deras frekvensdata om i termer av Strouhal-tal, och den visade sig stiga långsamt och sedan vara konstant över ett intervall av flödeshastigheter. Kim hittade ett liknande resultat: Strouhal-talet ökade med Reynolds-talet och förblev sedan konstant, som visas i den nedre bilden till höger. En annan unikhet med denna visselpipa är att återkopplingen är tillräckligt stark för att strålen avleds kroppsligt istället för att vara beroende av flödesinstabilitetsvirvelutveckling för att kontrollera den. Anordningens geometri antyder att det i huvudsak är en dipolkälla som arbetar i steg I med klass I (hydrodynamisk) återkoppling.

Monopol-dipol visselpipor

Det finns ett antal visselpipor som har egenskaperna hos både monopol- och dipolljudkällor. I flera av de visselpipor som beskrivs nedan är drivkällan dipol (i allmänhet en kantton) och den svarande källan är en monopol (i allmänhet ett rör eller en kavitet i närheten av dipolen).

₀ Den grundläggande skillnaden mellan dessa visselpipor från de som beskrivits ovan är att det nu finns två uppsättningar av karakteristiska variabler. För drivkällan är den karakteristiska hastigheten U och den karakteristiska dimensionen är L ₁ . _För den svarande källan är den karakteristiska hastigheten c , och den karakteristiska dimensionen är L2 , typiskt det korrigerade kavitetsdjupet eller rörlängden. De icke-dimensionella deskriptorerna för var och en av dessa är det vätskemekaniska Strouhal-numret och det akustiska Strouhal-numret. Kopplingen mellan dessa två siffror är frekvensens gemensamma karaktär.

Kanna visselpipa

Att blåsa över kanten på en kanna eller flaska kan skapa en nästan ren ton med låg frekvens. Drivkraften är flödet över kannas kant, så man kan förvänta sig ett kanttonsdipolljudfält. I det här fallet gör kantens krökning och rundhet en stark kantton osannolik. Eventuell periodicitet vid kanten är sannolikt nedsänkt i klass III-återkopplingen från kannans volym. Det ostadiga kantflödet skapar ett klassiskt Helmholtz-resonatorsvar , där den inre geometrin och kannas hals bestämmer den resulterande frekvensen. En resonansekvation är:

${\begin{aligned}\cot(kL)& ={\frac {A_{\text{c}}(L_{\text{o}}+\delta _{\text{e}}+\delta _{\text{i}})}{A_{\ text{o}}}}kL\\kL&=2\pi {\frac {fL}{c_{0}}}=2\pi {\text{St}}\end{aligned}}$

Det är en transcendental ekvation, där A _c är tvärsnittsarean av en cylindrisk hålighet med djupet L . Ao är arean av den cirkulära öppningen av djupet Lo , δe är den yttre ändkorrigeringen, δi _är den inre ändkorrigeringen och kL är Helmholtz _- talet (akustiskt Strouhal-tal med 2 _π tillagt ₎ . En cylindrisk hålighet 9 tum (230 mm) djup och 4,25 tum (108 mm) i diameter ansluts till en cirkulär öppning 1,375 tum (34,9 mm) i diameter och 1,375 tum (34,9 mm) djup. Den uppmätta frekvensen var nära 140 Hz. Om kaviteten fungerat som en kvartsvågsresonator skulle frekvensen ha varit 377 Hz; uppenbarligen inte en longitudinell resonans.

Ekvationen ovan indikerade 146 Hz och Nielsens ekvation indikerade 138 Hz. Tydligen drevs visselpipan av en hålighetsresonans. Detta är ett exempel på en visselpipa som körs i kanttoner, men resultatet är ett monopolljudfält.

Ton med djup hålighet

Flöde över en hålighet som anses djup kan skapa en visselpipa som liknar den över grunda håligheter. Djup särskiljs i allmänhet från grunt genom att hålrummets djup är större än bredden. Det finns två geometrier som har studerats. Den första geometrin är flöde utanför kaviteten, såsom på ett flygplan.

₀ Det finns två karakteristiska dimensioner (kavitetsbredd L , associerad med virvelutveckling, och hålighetsdjup D , associerad med akustisk respons). Det finns två karakteristiska hastigheter (flödeshastighet U , associerad med virvelutveckling, och ljudhastighet c , associerad med kavitetsrespons). Det visade sig att återkopplingen var klass III, och Strouhal-talen från 0,3 till 0,4 var associerade med ett enda virvelmönster (steg I) över gapet, medan Strouhal-tal från 0,6 till 0,9 var associerade med två virvlar över gapet (steg II).

Den andra geometrin är flöde i en kanal med en sidogren. Selamet och hans kollegor har gjort omfattande studier av visselfenomen i kanaler med sidogrenar som är stängda i ena änden. För dessa studier var kavitetsdjupet L och D var sidogrenens diameter. De vätskemekaniska Strouhal- och akustiska Strouhal-numren var:

${\begin{aligned}{\text{St}}&={\frac {fD}{U}}\\{\text{St}}_{\text{a}}&={\frac {fL_{1}}{c_{0}}}={\frac {2n+1 }{4}}\\L_{1}&=L\left(1+\beta {\frac {D}{L}}\right)\end{aligned}}$

En godtycklig konstant β användes för att representera impedansen vid förbindelsen mellan sidogrenen och kanalen. n var ett heltal som representerade stegnumret. De noterade att Strouhal-talet förblev konstant med ökad hastighet.

Piporgel

Piporgeln är ett annat exempel på en potentiellt dipolljudkälla som drivs som en monopolkälla. En luftstråle riktas mot en skarp kant och skapar flödessvängningar som i kanttonen. Kanten är en del av ett allmänt cylindriskt rör med längden L . Ett exempel visas i bilden till höger. Den instabila strålen driver vätska växelvis in i röret och ut. Strömlinjerna är tydligt förvrängda från de för den fria kanttonen. Det finns en stagnationspunkt mittemot källan. De streckade linjerna, färgade i rött, är de mest modifierade. De röda strömlinjerna i röret förstärks nu av det oscillerande flödet i röret, en överlagring av resistivt och reaktivt dipolflöde och resistivt akustiskt flöde.

Rörets längd avgör om rörets akustiska tryck eller hastighet är den dominerande inverkan på rörets frekvens. Enkla modeller av orgel-pipresonans är baserade på öppen-öppen rörresonans ( λ = L /2), men korrigeringar måste göras för att ta hänsyn till att ena änden av röret strålar in i det omgivande mediet och den andra strålar genom en slits med ett jetflöde. Boelkes och Hoffmann har gjort mätningar av ändkorrektion för öppna-öppna rör och härlett förhållandet δ = 0,33 D . Detta kan inte vara exakt, eftersom körändan inte är öppen.

₀ Strålningen ± impedans vid drivänden bör flytta röret mot ett λ /4-tillstånd, vilket ytterligare sänker frekvensen. Eftersom det finns två kopplade system, så finns det två karakteristikskalor. För rörkomponenten är den karakteristiska dimensionen L och den karakteristiska hastigheten är c ​​. För kanttonskomponenten är den karakteristiska dimensionen avståndet öppning till kant h och den karakteristiska hastigheten är strålens U. Det verkar som om systemets maximala oscillerande förstärkning skulle inträffa när den föredragna rörfrekvensen matchar den föredragna kanttonsfrekvensen med lämplig fas. Detta förhållande uttryckt i Strouhal-tal är:

${\begin{aligned}{\text{St}}_{\text{c}}&={\ frac {fL_{1}}{c_{0}}}&&{\text{St}}_{e}={\frac {fh}{U}}\\{\text{St}}_{\text {c}}&={\text{St}}_{\text{e}}{\frac {L_{1}}{h}}M\end{aligned}}$

Om dynamisk likhet gäller för båda resonanserna, föreslår den senare ekvationen hur orgelpipor skalas. Ekvationens skenbara enkelhet döljer viktiga variabla faktorer såsom den effektiva rörlängden L ₁ = L+ δ ₁ + δ ₂ , där δ ₁ är korrigering för den öppna änden och δ ₂ är korrigeringen för änden nära strålen. Strålstörningshastigheten (virvel) från öppning till kant kommer att variera med medelhastighet U , kantavstånd h och slitsbredd d , som föreslås i avsnittet Kantton .

Strouhal-förhållandet antyder att jet Mach-talet och förhållandet mellan effektiv rörlängd och kantavståndet är viktiga i en första approximation. Normal rördrift skulle vara en monopol ljudkälla i steg I med klass III återkoppling.

Flöjter, blockflöjter och piccolos

flöjt i indianstil

Ett antal musikinstrument, förutom piporgeln, är baserade på kanttonsfenomenet, de vanligaste är flöjten, piccolon (en liten version av flöjten) och blockflöjten. Flöjten kan blåsas lateralt om instrumentet eller i slutet, som de andra är. En inbyggd ändblåst flöjt visas i figuren.

₀ De är alla föremål för frekvenshopp när de är överblåsta, vilket tyder på dipol-monopolförhållandet. Monopolsaspekterna är relativt fixerade. Den karakteristiska dimensionen L2 för röret är fixerad _; den karakteristiska hastigheten c är fast. Den effektiva längden på röret är fixerad, eftersom strålningsimpedanserna i varje ände är fixerade. Till skillnad från piporgeln har dessa instrument dock sidoportar för att ändra resonansfrekvensen och därmed det akustiska Strouhal-numret.

Dipolaspekterna är också relativt fixerade. Strålens öppningsdimension och avståndet h till kanten är fasta. Även om jethastigheten U kan variera, är det vätskemekaniska Strouhal-talet relativt konstant och arbetar normalt i steg I. När det finns en faskoherent förstärkning av de två aspekterna fungerar de som klass III monopolkällor. Effektiviteten hos monopolstrålningen är avsevärt högre än dipolens, så dipolmönstret märks. Detaljerna om systemförstärkning och interaktion mellan dessa två dynamiska system är ännu inte helt avslöjade. Det är ett vittnesbörd om kunskaperna hos tidiga instrumenttillverkare att de kunde uppnå rätt portstorlekar och positioner för en given sedel utan vetenskapliga mätinstrument.

Se även

• Fåglarnas språk
• Sopa (docka)
• Visslande språk
• Visslade frikativ