Vågpaket

"Wave train" omdirigerar här. För matematikbegreppet, se Periodisk resande våg .

Ej att förväxla med Wave-gruppen .

Ett vågpaket utan dispersion (verklig eller imaginär del)

Ett vågpaket med dispersion

Inom fysik är ett vågpaket (eller vågtåg ) en kort "burst" eller " envelopp " av lokaliserad vågverkan som färdas som en enhet. Ett vågpaket kan analyseras till, eller kan syntetiseras från, en oändlig uppsättning av sinusformade komponentvågor av olika vågnummer , med faser och amplituder så att de interfererar konstruktivt endast över ett litet område av rymden, och destruktivt på andra ställen. Varje komponentvågfunktion , och därmed vågpaketet, är lösningar av en vågekvation . Beroende på vågekvationen kan vågpaketets profil förbli konstant (ingen spridning , se figur) eller så kan den ändras (spridning) under fortplantning.

Kvantmekaniken tillskriver vågpaketet en speciell betydelse; det tolkas som en sannolikhetsamplitud , dess norm kvadrerad beskriver sannolikhetstätheten att en partikel eller partiklar i ett visst tillstånd kommer att mätas ha en given position eller rörelsemängd. Vågekvationen är i detta fall Schrödinger-ekvationen , och genom dess tillämpning är det möjligt att härleda tidsutvecklingen för ett kvantmekaniskt system, liknande processen för Hamiltons formalism i klassisk mekanik . Den dispersiva karaktären hos lösningar av Schrödinger-ekvationen har spelat en viktig roll i att förkasta Schrödingers ursprungliga tolkning och acceptera Born-regeln .

I koordinatrepresentationen av vågen (som det kartesiska koordinatsystemet ) specificeras positionen för det fysiska objektets lokaliserade sannolikhet av positionen för paketlösningen. Ju smalare det rumsliga vågpaketet är, och ju bättre lokaliserat vågpaketets position, desto större blir spridningen i vågens rörelsemängd . Denna avvägning mellan spridning i position och spridning i momentum är ett karakteristiskt drag för Heisenbergs osäkerhetsprincip och kommer att illustreras nedan.

Historisk bakgrund

I början av 1900-talet blev det uppenbart att klassisk mekanik hade några stora brister. Isaac Newton föreslog ursprungligen idén att ljus kom i diskreta paket, som han kallade corpuscles , men det vågliknande beteendet hos många ljusfenomen fick snabbt forskare att gynna en vågbeskrivning av elektromagnetism . Det var inte förrän på 1930-talet som ljusets partikelnatur verkligen började bli allmänt accepterad inom fysiken. Utvecklingen av kvantmekaniken – och dess framgång med att förklara förvirrande experimentella resultat – låg till grund för denna acceptans. Således är ett av de grundläggande begreppen i formuleringen av kvantmekaniken att ljus kommer i diskreta buntar som kallas fotoner . Energin hos en foton är en funktion av dess frekvens,

$$E=h\nu .$$

Fotonens energi är lika med produkten av Planck-konstanten , h , och dess frekvens, ν . Detta löste ett problem i klassisk fysik, kallad ultraviolettkatastrofen .

Kvantmekanikens idéer fortsatte att utvecklas under hela 1900-talet. Bilden som utvecklades var av en partikelformig värld, med alla fenomen och materia gjorda av och interagerar med diskreta partiklar; emellertid beskrevs dessa partiklar av en sannolikhetsvåg. Interaktionerna, platserna och all fysik skulle reduceras till beräkningarna av dessa sannolikhetsamplituder.

Världens partikelliknande natur har bekräftats genom experiment under ett sekel, medan de vågliknande fenomenen kunde karakteriseras som konsekvenser av vågpaketaspekten av kvantpartiklar (se våg-partikeldualitet ) . Enligt komplementaritetsprincipen manifesterar de vågliknande och partikelliknande egenskaperna sig aldrig samtidigt, dvs i samma experiment; se dock Afshar-experimentet och den livliga diskussionen kring det.

Grundläggande beteenden

Positionera rymdsannolikhetstätheten för ett initialt Gaussiskt tillstånd instängt i en oändlig potentiell brunn som upplever periodisk kvanttunnel i en centrerad potentialvägg.

Icke-spridande

Som ett exempel på utbredning utan spridning , överväg våglösningar till följande vågekvation från klassisk fysik

$${\partial ^{2}u \over \partial t^{2}}=c^{2}\,\nabla ^{2}u,$$

där c är hastigheten för vågens utbredning i ett givet medium.

Med hjälp av fysiktidskonventionen, e − ^{iωt ,} har vågekvationen planvågslösningar

$$u(\mathbf {x} ,t)=e^{i{(\mathbf {k\cdot x} }-\omega t)},$$

var

$$\omega ^{2}=|\mathbf {k} |^{2}c^{2},$$

och $|\mathbf {k} |^{2}=k_{x}^{2}+k_{y}^{2}+k_{z}^{2}.$

Detta förhållande mellan ω och k bör vara giltigt så att den plana vågen är en lösning på vågekvationen. Det kallas en spridningsrelation .

För att förenkla, överväg bara vågor som utbreder sig i en dimension (utvidgning till tre dimensioner är enkel). Då är den allmänna lösningen

$$u(x,t)=Ae^{i(kx-\omega t )}+Be^{-i(kx+\omega t)},$$

där vi kan ta ω = kc . Den första termen representerar en våg som fortplantar sig i den positiva x -riktningen eftersom den endast är en funktion av x − ct ; den andra termen, som är en funktion av x + ct , representerar en våg som fortplantar sig i den negativa x -riktningen .

Ett vågpaket är en lokaliserad störning som är resultatet av summan av många olika vågformer . Om paketet är starkt lokaliserat behövs fler frekvenser för att tillåta den konstruktiva överlagringen i lokaliseringsregionen och destruktiv överlagring utanför regionen. Från de grundläggande lösningarna i en dimension kan en generell form av ett vågpaket uttryckas som

$$u(x,t)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\,\infty }A(k)~e^{i (kx-\omega (k)t)}\,dk.$$

Som i fallet med planvåg färdas vågpaketet till höger för ω ( k ) = kc , eftersom u ( x , t ) = F ( x − ct ) , och till vänster för ω ( k ) = − kc , eftersom u ( x , t ) = F ( x + ct ) .

Faktorn 1 ⁄ √ 2π kommer från Fouriertransformkonventioner . Amplituden A ( k ) innehåller koefficienterna för den linjära överlagringen av planvågslösningarna. Dessa koefficienter kan i sin tur uttryckas som en funktion av u ( x , t ) utvärderad vid t = 0 genom att invertera Fouriertransformationsrelationen ovan:

$$A(k)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\,\infty }u(x,0)~e^{- ikx}\,dx.$$

Till exempel att välja

$$u(x,0)=e^{-x^{2}+ik_{0}x},$$

vi får

$$A(k)={\frac {1}{\sqrt {2}}}e^{-{\frac {(k- k_{0})^{2}}{4}}},$$

och slutligen

$${\begin{aligned}u(x,t)&=e^{-(x-ct)^{2}+ik_{0}(x-ct)}\\&=e^{-( x-ct)^{2}}\left[\cos \left(2\pi {\frac {x-ct}{\lambda }}\right)+i\sin \left(2\pi {\frac { x-ct}{\lambda }}\right)\right].\end{aligned}}$$

Den icke-spridande fortplantningen av den verkliga eller imaginära delen av detta vågpaket presenteras i ovanstående animation.

Spridande

Positionera rymdsannolikhetstätheten för ett initialt Gaussiskt tillstånd som rör sig i en dimension med minimalt osäkert, konstant momentum i det fria rummet.

Däremot, som ett exempel på fortplantning, nu med dispersion , överväg istället lösningar till Schrödinger-ekvationen (icke-dimensionaliserad med 2Δ x , m och ħ satt lika med ett),

$$i{\partial \psi \over \partial t}=-{\frac {1}{2}}{\nabla ^{2}\psi } ,$$

ger spridningsförhållandet

$$\omega ={\frac {1}{2}}|\mathbf {k} |^{2}.$$

Återigen, begränsande uppmärksamheten till en dimension, lösningen till Schrödinger-ekvationen uppfyller initialvillkoret ${\textstyle \psi (x,0) ={\sqrt[{4}]{2/\pi }}\exp \left({-x^{2}+ik_{0}x}\right)} , representerar$ ett vågpaket lokaliserat i rymden vid ursprunget , ses vara

$${\begin{aligned}\psi (x,t)&={\frac {\sqrt[{4}]{2/\pi }}{\sqrt {1+2it}}}e^{- {\frac {1}{4}}k_{0}^{2}}~e^{-{\frac {1}{1+2it}}\left(x-{\frac {ik_{0}} {2}}\right)^{2}}\\&={\frac {\sqrt[{4}]{2/\pi }}{\sqrt {1+2it}}}e^{-{\ frac {1}{1+4t^{2}}}(x-k_{0}t)^{2}}~e^{i{\frac {1}{1+4t^{2}}}\ left((k_{0}+2tx)x-{\frac {1}{2}}tk_{0}^{2}\right)}~.\end{aligned}}$$

Ett intryck av det dispersiva beteendet hos detta vågpaket erhålls genom att titta på sannolikhetstätheten:

$$|\psi (x,t)|^{2}={\frac {\sqrt {2/\pi }}{\sqrt {1+4t^{2}}}}~e^{-{ \frac {2(x-k_{0}t)^{2}}{1+4t^{2}}}}~.$$

Det är uppenbart att detta dispersiva vågpaket, medan det rör sig med konstant grupphastighet k _o , delokaliseras snabbt: det har en bredd som ökar med tiden som √ 1 + 4 t ² → 2 t , så till slut diffunderar det till ett obegränsat område av rymden .

Momentumprofilen A ( k ) förblir invariant. Sannolikhetsströmmen är _

$$j=\rho v={\frac {1}{2i}}(\psi ^{*}\nabla \psi -\psi \nabla \psi ^{*})=\rho \left(k_{ 0}+{\frac {4t(x-k_{0}t)}{1+4t^{2}}}\höger).$$

Gaussiska vågpaket i kvantmekanik

Superposition av 1D plana vågor (blå) som summerar till att bilda ett kvantgaussiskt vågpaket (rött) som fortplantar sig åt höger medan det sprider sig. Blå prickar följer varje plan vågs fashastighet medan den röda linjen följer den centrala gruppens hastighet.

Positionera rymdsannolikhetstätheten för ett initialt Gaussiskt tillstånd instängt i en oändlig potentiell brunn som upplever periodisk kvanttunnel i en centrerad potentialvägg.

1D Gaussisk vågpaket, visat i det komplexa planet, för a =2 och k =4

Det ovan dispersiva Gaussiska vågpaketet, onormaliserat och precis centrerat vid origo, istället, vid t =0, kan nu skrivas i 3D, nu i standardenheter:

$$\psi (\mathbf {r} ,0)=e^{-\mathbf {r} \cdot \mathbf {r} /2a},$$

där a är ett positivt reellt tal, kvadraten på vågpaketets bredd ,

$$a=2\langle \mathbf {r} \cdot \mathbf {r} \rangle /3\langle 1\rangle =2(\Delta x)^{2}.$$

Fouriertransformen är också en Gauss i termer av vågnumret, t =0, k -vektorn, (med invers bredd,

$$1/a=2\langle \mathbf {k} \cdot \mathbf {k} \rangle /3\langle 1\rangle =2(\Delta p_{x}/\hbar )^{2},$$

så att

$$\Delta x\Delta p_{x}=\hbar /2,$$

dvs det mättar osäkerhetsrelationen ) ,

$$\psi (\mathbf {k} ,0)=(2\pi a)^{3/2}e^{-a\mathbf {k} \cdot \mathbf {k} /2}.$$

Varje separat våg roterar endast i tiden, så att den tidsberoende Fourier-transformerade lösningen är

${\begin{aligned}\Psi (\mathbf {k} ,t)&=(2\pi a)^{3/2}e^{-a\mathbf {k} \cdot \mathbf {k } /2}e^{-iEt/\hbar }\\&=(2\pi a)^{3/2}e^{-a\mathbf {k} \cdot \mathbf {k} /2-i (\hbar ^{2}\mathbf {k} \cdot \mathbf {k} /2m)t/\hbar }\\&=(2\pi a)^{3/2}e^{-(a+ i\hbar t/m)\mathbf {k} \cdot \mathbf {k} /2}.\end{aligned}}$

Den inversa Fouriertransformen är fortfarande en Gaussisk, men nu har parametern a blivit komplex, och det finns en övergripande normaliseringsfaktor.

$\Psi (\mathbf {r} ,t)=\left({a \over a+i\hbar t/m}\right)^{3/2}e^{-{\mathbf {r} \cdot \mathbf {r} \över 2(a+i\hbar t/m)}}.$

Integralen av Ψ över hela rymden är invariant, eftersom det är den inre produkten av Ψ med tillståndet nollenergi, vilket är en våg med oändlig våglängd, en konstant funktion av rymden. För varje energiegentillstånd η ( x ) , den inre produkten,

$$\langle \eta |\psi \rangle =\int \eta (\mathbf {r} )\psi (\mathbf {r} )d ^{3}\mathbf {r} ,$$

ändras endast i tid på ett enkelt sätt: dess fas roterar med en frekvens som bestäms av energin η . När η har noll energi, som den oändliga våglängdsvågen, förändras den inte alls.

Integralen ∫ |Ψ| ² d ³ r är också invariant, vilket är ett uttalande om bevarande av sannolikhet. Explicit,

$P(r)=|\Psi |^ {2}=\Psi ^{*}\Psi =\left({a \over {\sqrt {a^{2}+(\hbar t/m)^{2}}}}\right)^{3 }~e^{-{a\,\mathbf {r} \cdot \mathbf {r} \over a^{2}+(\hbar t/m)^{2}}},$

där √ a är bredden av P ( r ) vid t = 0 ; r är avståndet från origo; hastigheten på partikeln är noll; och tidsursprunget t = 0 kan väljas godtyckligt.

Gaussans bredd är den intressanta storhet som kan avläsas från sannolikhetstätheten, | Ψ| ² ,

$${\sqrt {a^{2}+(\hbar t/m)^{2} \over a}}.$$

Denna bredd växer så småningom linjärt i tiden, som ħt /( m √ a ) , vilket indikerar vågpaketspridning .

Till exempel, om ett elektronvågspaket initialt är lokaliserat i ett område med atomära dimensioner (dvs. 10 ⁻¹⁰ m) fördubblas paketets bredd på cirka 10 ⁻¹⁶ s. Uppenbarligen sprider sig partikelvågspaket mycket snabbt (i fritt utrymme): Till exempel, efter 1 ms, kommer bredden att ha vuxit till ungefär en kilometer.

Denna linjära tillväxt är en återspegling av den (tidsinvarianta) momentumosäkerheten: vågpaketet är begränsat till en smal Δ x = √ a /2 , och har sålunda ett momentum som är osäkert (enligt osäkerhetsprincipen ) med mängden ħ / √ 2 a , en spridning i hastighet på ħ/m √ 2 a , och därmed i den framtida positionen med ħt /m √ 2 a . Osäkerhetsrelationen är då en strikt ojämlikhet, mycket långt ifrån mättnad, faktiskt! Den initiala osäkerheten Δ x Δ p = ħ /2 har nu ökat med en faktor ħt/ma (för stort t ).

Det luftiga vågtåget

I motsats till ovanstående Gaussiska vågpaket, har det observerats att en viss vågfunktion baserad på luftiga funktioner , fortplantar sig fritt utan enveloppspridning och bibehåller sin form. Den accelererar oförvrängd i frånvaro av ett kraftfält: ψ = Ai( B ( x − B ³ t ² )) exp( iB ³ t ( x − 2 B ³ t ² /3)) . (För enkelhetens skull ħ = 1 , m = 1/2 och B en konstant, jfr icke-dimensionalisering .)

Trunkerad bild av tidsutvecklingen för den luftiga fronten i fasrymden. (Klicka för att animera.)

Ändå finns det ingen dissonans med Ehrenfests teorem i denna kraftfria situation, eftersom tillståndet både är icke-normaliserbart och har ett odefinierat (oändligt) ⟨ x ⟩ för alla tider. (I den mån det går att definiera, ⟨ p ⟩ = 0 för alla tider, trots den uppenbara accelerationen av fronten.)

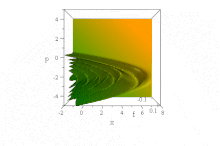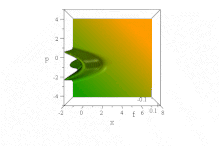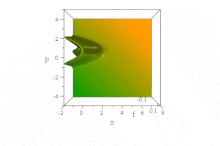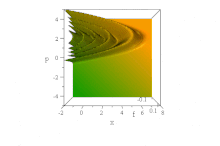
I fasrymden är detta uppenbart i det rena tillståndet Wigner-kvasisannolikhetsfördelningen av detta vågtåg, vars form i x och p är invariant när tiden fortskrider, men vars egenskaper accelererar åt höger, i accelererande paraboler B ( x − B ³ t ² ) + ( p / B − tB ² ) ² = 0 ,

$$W(x,p;t)=W(xB^{3}t^{2},pB^{3}t;0)={1 \över 2^{1/3}\pi B} ~\mathrm {Ai} \left(2^{2/3}\left(Bx+{p^{2} \over B^{2}}-2Bpt\right)\right).$$

Notera att momentumfördelningen som erhålls genom att integrera över alla x är konstant. Eftersom detta är sannolikhetstätheten i momentumrymden är det uppenbart att vågfunktionen i sig inte är normaliserbar.

Under 2018 uppnåddes den första experimentella observationen av den kubiska fasen av accelererande Airy-vågpaket genom ett samarbete mellan forskare från israeliska, tyska och amerikanska universitet.

Gratis propagator

Den smala breddgränsen för den gaussiska vågpaketlösningen som diskuteras är den fria propagatorkärnan K . För andra differentialekvationer brukar detta kallas för Greens funktion, men inom kvantmekaniken är det traditionellt att reservera namnet Greens funktion för tids-Fouriertransformen av K .

Återgå till en dimension för enkelhetens skull, med m och ħ satta lika med ett, när a är den oändliga kvantiteten ε , det Gaussiska initialtillståndet, omskalat så att dess integral är ett,

$$\psi _{0}(x)={1 \over {\sqrt {2\pi \varepsilon }}}e^{-{x ^{2} \over 2\varepsilon }}\,$$

blir en deltafunktion , δ ( x ) , så att dess tidsutveckling,

$$K_{t}(x)={1 \over {\sqrt {2\pi (it+\varepsilon )}}}e^{-x^{2} \over 2it+\varepsilon }\,$$

ger propagatorn.

Observera att ett mycket smalt initialt vågpaket omedelbart blir oändligt brett, men med en fas som är snabbare oscillerande vid stora värden på x . Detta kan tyckas konstigt - lösningen går från att vara lokaliserad vid ett tillfälle till att vara "överallt" vid alla senare tidpunkter , men det är en återspegling av den enorma momentumosäkerheten hos en lokaliserad partikel, som förklarats ovan.

Observera vidare att normen för vågfunktionen är oändlig, vilket också är korrekt, eftersom kvadraten på en deltafunktion är divergerande på samma sätt.

Faktorn som involverar ε är en oändlig storhet som är till för att säkerställa att integraler över K är väldefinierade. I gränsen som ε → 0 , blir K rent oscillerande, och integraler av K är inte absolut konvergenta. I återstoden av detta avsnitt kommer det att sättas till noll, men för att alla integrationer över mellantillstånd ska vara väl definierade, ska gränsen ε →0 tas först efter att sluttillståndet har beräknats.

Propagatorn är amplituden för att nå punkt x vid tidpunkten t , när man börjar vid origo, x =0. Genom translationsinvarians är amplituden för att nå en punkt x när man börjar vid punkt y samma funktion, bara nu översatt,

$$K_{t}(x,y)=K_{t}(xy)={1 \over {\sqrt {2\pi it}}}e^{i(xy)^{2} \over 2t }\,.$$

I gränsen när t är litet går propagatorn till en deltafunktion

$$\lim _{t\to 0}K_{t}(xy)=\delta (xy)~,$$

men bara i betydelsen distributioner : Integralen av denna kvantitet multiplicerad med en godtycklig differentierbar testfunktion ger testfunktionens värde vid noll.

För att se detta, notera att integralen över hela rummet av K är lika med 1 hela tiden,

$$\int K_{t}(x)dx=1\,,$$

eftersom denna integral är den inre produkten av K med den enhetliga vågfunktionen. Men fasfaktorn i exponenten har en rumslig derivata som inte är noll överallt utom vid origo, och så när tiden är liten finns det snabba fasavbrott vid alla utom en punkt. Detta är strikt sant när gränsen ε →0 tas i slutet.

Så fortplantningskärnan är den (framtida) tidsutvecklingen av en deltafunktion, och den är kontinuerlig på sätt och vis: den går till den initiala deltafunktionen vid små tidpunkter. Om den initiala vågfunktionen är en oändligt smal spik vid position y ,

$$\psi _{0}(x)=\delta (xy)\,,$$

det blir den oscillerande vågen,

$$\psi _{t}(x)={1 \over {\sqrt {2\pi it}}}e^{i(xy)^{2}/2t}\,.$$

Nu, eftersom varje funktion kan skrivas som en viktad summa av sådana smala spikar,

$$\psi _{0}(x)=\int \psi _{0}(y)\delta (xy)dy\ ,,$$

₀ tidsutvecklingen för varje funktion ψ bestäms av denna fortplantningskärna K ,

$\psi _{t}(x)=\int \psi _{0}(y){1 \over {\sqrt {2\pi it}}}e^{i(xy)^{2} /2t}dy\,.$

Detta är alltså ett formellt sätt att uttrycka den grundläggande lösningen eller den allmänna lösningen . Tolkningen av detta uttryck är att amplituden för en partikel som ska hittas vid punkt x vid tidpunkten t är amplituden som den startade vid y , gånger amplituden som den gick från y till x , summerad över alla möjliga startpunkter . Med andra ord är det en faltning av kärnan K med det godtyckliga initiala villkoret ψ ₀ ,

$$\psi _{t}=K*\psi _{0}\,.$$

Eftersom amplituden för att resa från x till y efter en tid t + t ' kan betraktas i två steg, lyder propagatorn kompositionens identitet,

$$\int K(xy;t)K(yz;t' )dy=K(xz;t+t')~,$$

vilket kan tolkas enligt följande: amplituden för att resa från x till z i tiden t + t ' är summan av amplituden för att resa från x till y i tiden t , multiplicerad med amplituden för att resa från y till z i tiden t ', summerat över alla möjliga mellantillstånd y . Detta är en egenskap hos ett godtyckligt kvantsystem, och genom att dela upp tiden i många segment gör det att tidsutvecklingen kan uttryckas som en vägintegral .

Analytisk fortsättning till diffusion

Se även: Värmeekvation § Grundläggande lösningar och Värmekärna

Spridningen av vågpaket inom kvantmekaniken är direkt relaterad till spridningen av sannolikhetstätheter i diffusion . För en partikel som går slumpmässigt , uppfyller sannolikhetstäthetsfunktionen vid vilken punkt som helst diffusionsekvationen ( se även värmeekvationen) ,

$${\partial \over \partial t}\rho ={1 \over 2}{\partial ^{2} \over \partial x^{2 }}\rho ~,$$

där faktorn 2, som kan tas bort genom att skala om antingen tid eller rum, endast är för bekvämlighet.

En lösning av denna ekvation är den spridande gaussiska,

$$\rho _{t}(x)={1 \over {\sqrt {2\pi t}}}e^{-x ^{2} \over 2t}~,$$

och eftersom integralen av ρ _t är konstant medan bredden blir smal vid små tidpunkter, närmar sig denna funktion en deltafunktion vid t = 0,

$$\lim _{t\to 0}\rho _{t}(x)=\delta (x)$$

återigen endast i betydelsen distributioner, så att

$$\lim _{t\to 0}\int _{x}f(x)\rho _{t}(x)= f(0)$$

för varje smidig testfunktion f .

Den spridande Gaussian är fortplantningskärnan för diffusionsekvationen och den lyder faltningsidentiteten ,

$$K_{t+t'}=K_{t}*K_{t'}\,,$$

som tillåter diffusion att uttryckas som en vägintegral. Propagatorn är exponentialen för en operator H ,

$$K_{t}(x)=e^{-tH}\,,$$

som är den oändliga diffusionsoperatorn,

$$H=-{\nabla ^{2} \over 2}\,.$$

En matris har två index, vilket i kontinuerligt utrymme gör den till en funktion av x och x '. I det här fallet, på grund av translationsinvarians, beror matriselementet K endast på skillnaden i positionen, och ett bekvämt missbruk av notation är att referera till operatorn, matriselementen och funktionen av skillnaden med samma namn:

$$K_{t}(x,x')=K_{t}(xx')\,.$$

Translationsinvarians innebär att kontinuerlig matrismultiplikation,

$$C(x,x'')=\int _{x'}A(x, x')B(x',x'')\,,$$

är i huvudsak faltning,

$$C(\Delta )=C(xx'')=\int _{x'}A(xx')B(x'-x'')=\int _{y}A(\Delta -y )Förbi)\,.$$

Exponentialen kan definieras över ett intervall av t: n som inkluderar komplexa värden, så länge som integraler över fortplantningskärnan förblir konvergenta,

$$K_{z}(x)=e^{-zH}\,.$$

Så länge som den reella delen av z är positiv, för stora värden på x , minskar K exponentiellt, och integraler över K är verkligen absolut konvergenta.

Gränsen för detta uttryck för z som närmar sig den rena imaginära axeln är ovanstående Schrödinger-propagator som stött på,

$$K_{t}^{\rm {Schr}}=K_{it+\varepsilon }=e^{- (it+\varepsilon )H}\,,$$

som illustrerar ovanstående tidsutveckling av Gausserna.

Från den grundläggande identiteten av exponentiering, eller vägintegration,

$$K_{z}*K_{z'}=K_{z+z'}\,$$

gäller för alla komplexa z- värden, där integralerna är absolut konvergenta så att operatorerna är väldefinierade.

Således kvantutveckling av en Gauss, som är den komplexa diffusionskärnan K ,

$$\psi _{0}(x)=K_{a}(x)=K_{a}*\delta (x)\ ,$$

uppgår till det tidsutvecklade tillståndet,

$$\psi _{t}=K_{it}*K_{a}=K_{a+it}\,.$$

Detta illustrerar ovanstående diffusiva form av de komplexa gaussiska lösningarna,

$$\psi _{t}(x)={1 \over {\sqrt {2\pi (a+it)}}}e^{-{x^{2} \over 2(a+it) }}\,.$$

Se även

• Vinka
• Vågutbredning
• Fourieranalys
• Grupphastighet
• Fashastighet
• Fri partikel
• Sammanhängande stater
• Vågform
• Vågkomponent
• Materia våg
• Puls (signalbehandling)
• Puls (fysik)
• Schrödinger ekvation
• Introduktion till kvantmekanik
• Soliton

Anteckningar

• Einstein, Albert (1905), "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (On a Heuristic Viewpoint Concerning the Production and Transformation of Light)" ( PDF) , Annalen der Physik , 17 (6): 132–148, Bibcode : 1905AnP...322..132E , doi : 10.1002/andp.19053220607 Detta annus mirabilis -dokument om den fotoelektriska effekten mottogs av Annalen der Physik 18 mars 1905.
• Schiff, Leonard I. (1968), Quantum mechanics (tredje upplagan), London: McGraw-Hill
•   Joy Manners (2000), Quantum Physics: An Introduction , CRC Press, s. 53–56, ISBN 978-0-7503-0720-8
•   Pauli, Wolfgang (2000), Wave Mechanics: Volym 5 av Pauli Lectures on Physics , Books on Physics, Dover Publications , ISBN 978-0-486-41462-1
•   Abers, E.; Pearson, Ed (2004), Quantum Mechanics , Addison Wesley , Prentice-Hall Inc. , ISBN 978-0-13-146100-0
• Richard Fitzpatrick, Oscillations and Waves
• Berry, MV; Balazs, NL (1979), "Nonspreading wave packets", Am J Phys , 47 (3): 264–267, Bibcode : 1979AmJPh..47..264B , doi : 10.1119/1.11855
•   Jackson, JD (1975), Classical Electrodynamics (2:a upplagan), New York: John Wiley & Sons , Inc., ISBN 978-0-471-43132-9
•    Feynman, RP ; Hibbs, AR (1965), Quantum Mechanics and Path Integrals , New York: McGraw-Hill , ISBN 978-0-07-020650-2 ( Dover , 2010, ISBN 0-486-47722-3 .)
• Wheeler, Nicholas (2004), Anmärkningar angående energin hos ett Gaussiskt vågpaket (PDF)

externa länkar

• Läromedel relaterat till vågpaketrörelse på Wikiversity
• Ordboksdefinitionen av vågpaket på Wiktionary
• 1d Wave-paketplot i Google
• 1d vågtåg och sannolikhetstäthetsplot i Google
• 2d Wave-paketplot i Google
• 2d Wave tågplan i Google
• 2D sannolikhetstäthet plot i Google
• Kvantfysik online : Interaktiv simulering av ett gratis vågpaket
• Web-Schrödinger : Interaktiv 2D-vågpaketdynamiksimulering
• En simulering av ett vågpaket i 2D (enligt FOURIER-Synthesis in 2D)
• Curtright, TL, tidsberoende Wigner-funktioner