Tetraedrisk molekylär geometri

Tetraedrisk molekylär geometri
Tetrahedral-3D-balls.png
Exempel CH 4 , MnO
− 4
Punktgrupp T d
Samordningsnummer 4
Bindningsvinkel(ar) ≈ 109,5°
μ (polaritet) 0

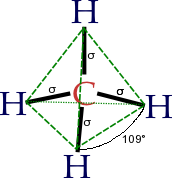
I en tetraedrisk molekylär geometri är en central atom belägen i mitten med fyra substituenter som finns i hörnen av en tetraeder . Bindningsvinklarna är cos −1 (− 1 ⁄ 3 ) = 109,4712206...° ≈ 109,5° när alla fyra substituenterna är desamma, som i metan ( CH 4 ) såväl som dess tyngre analoger . Metan och andra perfekt symmetriska tetraedriska molekyler tillhör punktgruppen T d , men de flesta tetraedriska molekyler har lägre symmetri . Tetraedriska molekyler kan vara kirala .

Tetraedrisk bindningsvinkel

Beräkna bindningsvinklar för en symmetrisk tetraedrisk molekyl med hjälp av en punktprodukt

Bindningsvinkeln för en symmetrisk tetraedrisk molekyl som CH 4 kan beräknas med hjälp av punktprodukten av två vektorer . Som visas i diagrammet kan molekylen inskrivas i en kub med den fyrvärda atomen (t.ex. kol ) i kubcentrum som är ursprunget till koordinaterna, O. De fyra envärda atomerna (t.ex. väten) finns i fyra hörn av kuben (A, B, C, D) vald så att inga två atomer är i angränsande hörn förbundna med endast en kubkant. Om kantlängden på kuben väljs som 2 enheter, så motsvarar de två bindningarna OA och OB vektorerna a = (1, –1, 1) och b = (1, 1, –1), och bindningsvinkeln θ är vinkeln mellan dessa två vektorer. Denna vinkel kan beräknas från punktprodukten av de två vektorerna, definierade som a • b = || en || || b || cos θ där || en || anger längden på vektor a . Som visas i diagrammet är punktprodukten här –1 och längden på varje vektor är √3, så att cos θ = –1/3 och den tetraedriska bindningsvinkeln θ = arccos ( –1/3 ) ≃ 109,47°.

Exempel

Huvudgruppskemi

Den tetraedriska molekylen metan ( CH 4 )

Bortsett från praktiskt taget alla mättade organiska föreningar är de flesta föreningar av Si, Ge och Sn tetraedriska. Ofta har tetraedriska molekyler multipel bindning till de yttre liganderna, som i xenontetroxid (XeO 4 ), perkloratjonen ( ClO − 4 ), sulfatjonen ( SO 2− 4 ), fosfatjonen ( PO 3− 4 ). Tiazyltrifluorid ( SNF 3 ) är tetraedrisk, med en trippelbindning mellan svavel och kväve.

Andra molekyler har ett tetraedriskt arrangemang av elektronpar runt en central atom; till exempel ammoniak ( NH 3 ) med kväveatomen omgiven av tre väten och ett ensamt par . Men den vanliga klassificeringen tar bara hänsyn till de bundna atomerna och inte det ensamma paret, så att ammoniak faktiskt betraktas som pyramidal . Vinklarna H–N–H är 107°, sammandragna från 109,5°. Denna skillnad tillskrivs påverkan av det ensamma paret som utövar ett större frånstötande inflytande än en bunden atom.

Övergångsmetallkemi

0 Återigen är geometrin utbredd, särskilt för komplex där metallen har d- eller dio - konfiguration. Illustrativa exempel inkluderar Pd[P(C6H5 trifenylfosfin titantetraklorid 3 ] 4 ) , )palladium(0) ( ( ) nickelkarbonyl Ni ( CO) 4 ) och ( TiCl4 ). Många komplex med ofullständigt fyllda d-skal är ofta tetraedriska, t.ex. tetrahaliderna av järn(II), kobolt(II) och nickel(II).

Vattenstruktur

I gasfasen har en enda vattenmolekyl en syreatom omgiven av två väten och två ensamma par, och H 2 O -geometrin beskrivs helt enkelt som böjd utan att ta hänsyn till de icke-bindande ensamma paren.

Men i flytande vatten eller i is bildar de ensamma paren vätebindningar med närliggande vattenmolekyler. Det vanligaste arrangemanget av väteatomer runt ett syre är tetraedriskt med två väteatomer kovalent bundna till syre och två bundna med vätebindningar. Eftersom vätebindningarna varierar i längd är många av dessa vattenmolekyler inte symmetriska och bildar övergående oregelbundna tetraedrar mellan deras fyra associerade väteatomer.

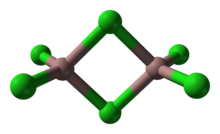
Bitetraedriska strukturer

Många föreningar och komplex antar bitetraedriska strukturer. I detta motiv delar de två tetraedrarna en gemensam kant. Den oorganiska polymeren kiseldisulfid har en oändlig kedja av kantdelade tetraedrar. I ett helt mättat kolvätesystem har den bitetraedriska molekylen C 8 H 6 föreslagits som en kandidat för molekylen med kortast möjliga kol-kol enkelbindning .

Bitetraedrisk galliumtriklorid Ga2Cl6 ( struktur antagen av Al2Br6 " ) aluminiumtribromid ( " ") och " .

Undantag och snedvridningar

Inversion av tetraedrar förekommer i stor utsträckning inom organisk kemi och huvudgruppskemi. Den så kallade Walden-inversionen illustrerar de stereokemiska konsekvenserna av inversion vid kol. Kväveinversion i ammoniak medför också övergående bildning av plan NH 3 .

Inverterad tetraedrisk geometri

Geometriska begränsningar i en molekyl kan orsaka en allvarlig förvrängning av idealiserad tetraedrisk geometri. I föreningar med "inverterad" tetraedrisk geometri vid en kolatom, är alla fyra grupper bundna till detta kol på ena sidan av ett plan. Kolatomen ligger vid eller nära toppen av en fyrkantig pyramid med de andra fyra grupperna i hörnen.

Inverted carbon

De enklaste exemplen på organiska molekyler som uppvisar inverterad tetraedrisk geometri är de minsta propellaner , såsom [1.1.1]propellane ; eller mer allmänt paddlanes och pyramidan ([3.3.3.3]fenestrane). Sådana molekyler är vanligtvis ansträngda , vilket resulterar i ökad reaktivitet.

Planarisering

En tetraeder kan också förvrängas genom att öka vinkeln mellan två av bindningarna. I det extrema fallet blir det tillplattad resultat. För kol kan detta fenomen observeras i en klass av föreningar som kallas fenestraner . [ citat behövs ]

Tetraedriska molekyler utan central atom

Ett fåtal molekyler har en tetraedrisk geometri utan någon central atom. Ett oorganiskt exempel är tetrafosfor ( P 4 ) som har fyra fosforatomer vid hörn av en tetraeder och var och en bunden till de andra tre. Ett organiskt exempel är tetrahedran ( C 4 H 4 ) med fyra kolatomer vardera bundna till ett väte och de andra tre kolatomerna. I detta fall är den teoretiska C−C−C bindningsvinkeln bara 60° (i praktiken blir vinkeln större på grund av böjda bindningar ), vilket representerar en stor grad av töjning.

Se även

  1. ^ Alger, Nick. "Vinkel mellan 2 ben av en tetraeder" . Arkiverad från originalet 2018-10-03.
  2. ^ Brittin, WE (1945). "Valensvinkeln för den tetraedriska kolatomen". J. Chem. Educ. 22 (3): 145. Bibcode : 1945JChEd..22..145B . doi : 10.1021/ed022p145 .
  3. ^   Miessler, GL; Tarr, DA (2004). Oorganisk kemi (3:e upplagan). Pearson/Prentice Hall. ISBN 0-13-035471-6 .
  4. ^   Mason, PE; Brady, JW (2007). " "Tetrahedralitet" och förhållandet mellan kollektiv struktur och radiella distributionsfunktioner i flytande vatten". J. Phys. Chem. B . 111 (20): 5669–5679. doi : 10.1021/jp068581n . PMID 17469865 .
  5. ^ Xie, Yaoming och Henry F. Schaefer. "Den bitetraedriska molekylen C8H6: Det kortaste möjliga CC-bindningsavståndet för ett mättat kolväte?" Chemical Physics Letters 161 (1989): 516-518.
  6. ^   Xie, Yaoming; Schaefer, Henry F. (1989-09-29). "Den bitetraedriska molekylen C8H6: Det kortaste möjliga CC-bindningsavståndet för ett mättat kolväte?" . Bokstäver i kemisk fysik . 161 (6): 516–518. Bibcode : 1989CPL...161..516X . doi : 10.1016/0009-2614(89)87031-9 . ISSN 0009-2614 .
  7. ^ Wiberg, Kenneth B. (1984). "Inverterade geometrier vid kol". Enl. Chem. Res. 17 (11): 379–386. doi : 10.1021/ar00107a001 .
  8. ^ a b Joseph P. Kenny; Karl M. Krueger; Jonathan C. Rienstra-Kiracofe; Henry F. Schaefer III (2001). " C5H4 : Pyramidan och dess lågt liggande isomerer " . J. Phys. Chem. A . 105 (32): 7745–7750. Bibcode : 2001JPCA..105.7745K . doi : 10.1021/jp011642r .
  9. ^ a b Lewars, E. (1998). "Pyramidane: en ab initio studie av den potentiella energiytan C 5 H 4 ". Journal of Molecular Structure: THEOCHEM . 423 (3): 173–188. doi : 10.1016/S0166-1280(97)00118-8 .
  10. ^ IUPAC , kompendium av kemisk terminologi , 2nd ed. ("Guldboken") (1997). Online korrigerad version: (2006–) " paddlanes ". doi : 10.1351/goldbook.P04395

externa länkar

Hämtad från " https://en.wikipedia.org/w/index.php?title=Tetrahedral_molecular_geometry&oldid=1085778525 "