Stokastisk portföljteori

Stokastisk portföljteori ( SPT ) är en matematisk teori för att analysera aktiemarknadens struktur och portföljbeteende som introducerades av E. Robert Fernholz 2002. Den är beskrivande i motsats till normativ, och överensstämmer med det observerade beteendet på faktiska marknader. Normativa antaganden, som ligger till grund för tidigare teorier som modern portföljteori (MPT) och kapitaltillgångsprissättningsmodellen ( CAPM), saknas i SPT.

SPT använder kontinuerliga slumpmässiga processer (särskilt kontinuerliga semi-martingales) för att representera priserna på enskilda värdepapper. Processer med diskontinuiteter, såsom hopp, har också inkorporerats* i teorin (*overifierbart påstående på grund av saknad citering!).

Aktier, portföljer och marknader

SPT tar hänsyn till aktier och aktiemarknader , men dess metoder kan också tillämpas på andra tillgångsklasser . En aktie representeras av dess prisprocess, vanligtvis i den logaritmiska representationen . Om marknaden är en samling aktiekursprocesser $X_{i},$ för $i=1,\dots ,n,$ var och en definierad av en kontinuerlig semimartingal

$d\log X_{i}(t)=\gamma _{i}(t)\,dt+\summa _{\nu =1}^{d}\xi _{i\nu}(t)\,dW_{\nu}(t)$

där $W:=(W_{1},\dots ,W_{d})$ är en $n$ -dimensionell Brownsk rörelseprocess (Wiener) med $d\geq n$ , och processerna $\gamma _{i}$ och $\xi _{i\nu }$ är progressivt mätbara med avseende på den Brownska filtrationen $\{{\mathcal {F}}_{t}\}=\{{\mathcal {F}}_{t}^{W}\ }$ . I denna representation kallas ${\displaystyle \gamma _{i}(t)} (sammansatt)$ tillväxthastigheten för $X_{i},$ och kovariansen mellan $\log X_{i}$ och $\log X_{j}$ är $\sigma _{ij}(t)=\sum _{\nu =1}^{d}\xi _{i\nu}(t)\xi _{j\nu}(t).$ Det antas ofta att för all $i,$ processen $\xi _{i,1}^{2 }(t)+\cdots +\xi _{id}^{2}(t)$ är positiv, lokalt kvadratintegrerbar och växer inte för snabbt som $t\rightarrow \infty .$

Den logaritmiska representationen är ekvivalent med den klassiska aritmetiska representationen som använder avkastningsgraden $\alpha _{i}(t),$ men tillväxttakten kan vara en meningsfull indikator på långsiktig prestation av en finansiell tillgång, medan avkastningen har en bias uppåt. Relationen mellan avkastningen och tillväxttakten är

$\alpha _{i}(t)=\gamma _{i}(t)+{\frac {\sigma _{ ii}(t)}{2}}$

Den vanliga konventionen i SPT är att anta att varje aktie har en enda aktie utestående, så $X_{i}(t)$ representerar den totala kapitaliseringen av i { $displaystyle i}$ -th aktien vid tid $t,$ och $X(t)=X_{1}(t)+\cdots +X_{n }(t)$ är marknadens totala kapitalisering. Utdelning kan inkluderas i denna representation, men utelämnas här för enkelhets skull.

En investeringsstrategi $\pi =(\pi _{1},\cdots ,\pi _{n})$ är en vektor av avgränsade, progressivt mätbara processer; kvantiteten $\pi _{i}(t)$ representerar andelen av den totala förmögenheten som investerats i den $i$ -:e aktien vid tidpunkten $t$ , och $\pi _{0}(t):=1-\summa _{i=1}^{n}\pi _{i} (t)$ är andelen hamstrad (investerad på en penningmarknad med nollränta). Negativa vikter motsvarar korta positioner. Kontantstrategin $\kappa \equiv 0(\kappa _{0}\equiv 1)$ behåller all rikedom på penningmarknaden. En strategi $\pi$ kallas portfölj , om den är fullt investerad på aktiemarknaden, det vill säga $\pi _{1}( t)+\cdots +\pi _{n}(t)=1$ gäller, hela tiden.

Värdeprocessen $Z_{\pi }$ för en strategi $\pi$ är alltid positiv och uppfyller

$d\log Z_{\pi }(t) =\summa _{i=1}^{n}\pi _{i}(t)\,d\log X_{i}(t)+\gamma _{\pi }^{*}(t)\ ,dt$

där processen $\gamma _{\pi }^{*}$ kallas överskottstillväxthastighetsprocessen och ges av

$\gamma _{\pi }^{*}(t):={\frac {1}{2}}\summa _{i=1}^{n}\pi _{i}( t)\sigma _{ii}(t)-{\frac {1}{2}}\sum _{i,j=1}^{n}\pi _{i}(t)\pi _{j }(t)\sigma _{ij}(t)$

Detta uttryck är icke-negativt för en portfölj med icke-negativa vikter $\pi _{i}(t)$ och har använts vid kvadratisk optimering av aktieportföljer, vars specialfall är optimering med avseende på den logaritmiska hjälpfunktionen.

Marknadsviktsprocesserna , _

$\mu _{i}(t):={\frac {X_{i}(t) }{X_{1}(t)+\cdots +X_{n}(t)}}$

där $i=1,\dots ,n$ definierar marknadsportföljen $\mu$ . Med initialvillkoret $Z_{\mu }(0)=X(0),$ kommer den associerade värdeprocessen att uppfylla $Z_{\mu }(t)=X(t)$ för alla $t.$

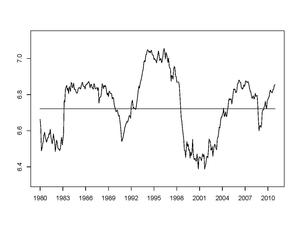
Figur 1 visar entropin på den amerikanska aktiemarknaden under perioden 1980 till 2012, med axeln vid medelvärdet under perioden. Även om entropin fluktuerar över tid, indikerar dess beteende att det finns en viss stabilitet på aktiemarknaden. Karakterisering av denna stabilitet är ett av målen med SPT.

Ett antal villkor kan ställas på en marknad, ibland för att modellera faktiska marknader och ibland för att betona vissa typer av hypotetiska marknadsbeteenden. Några vanliga villkor är:

1. En marknad är icke degenererad om egenvärdena för kovariansmatrisen $(\sigma _{ij}(t))_{1\leq i,j\leq n}$ är avgränsade från noll. Den har begränsad varians om egenvärdena är begränsade.
2. En marknad är koherent om $\operatörsnamn {lim} _{t\rightarrow \infty }t^{-1}\log(\mu _{i}(t))=0$ för alla $i=1,\dots ,n.$
3. En marknad är diversifierad på $[0,T]$ om det finns $\varepsilon >0$ så att $\mu _{\ max }(t)\leq 1-\varepsilon$ för $t\in [0,T].$
4. En marknad är svagt diversifierad på $\displaystyle [0,T]}$ om det finns $\varepsilon >0$ så att

${\frac {1}{T}}\int _{0}^{T}\mu _{\max }(t)\, dt\leq 1-\varepsilon$

Mångfald och svag mångfald är ganska svaga villkor, och marknaderna är i allmänhet mycket mer olika än vad som skulle testas av dessa ytterligheter. Ett mått på marknadens mångfald är marknadsentropi , definierad av

$S(\mu (t))=-\sum _{i=1}^{n}\mu _{i}(t)\log(\mu _{i}(t)).$

Stokastisk stabilitet

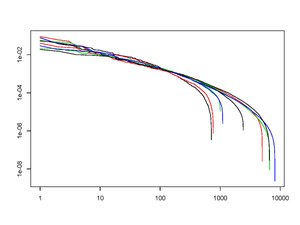
Figur 2 visar de (rankade) kapitalfördelningskurvorna i slutet av vart och ett av de senaste nio decennierna. Denna log-log plot har uppvisat anmärkningsvärd stabilitet under långa tidsperioder. Studiet av sådan stabilitet är ett av huvudmålen för SPT.

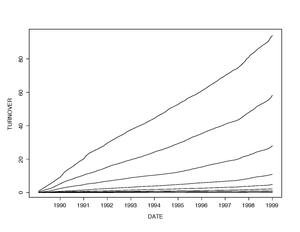
Figur 3 visar de "kumulativa omsättningsprocesserna" i olika led under loppet av ett decennium. Som väntat ökar omsättningen när man går nerför kapitaliseringsstegen. Det finns också en uttalad linjär tillväxt i tid över alla visade led.

Vi betraktar vektorprocessen $(\mu _{(1)}(t),\dots ,\mu _{(n )}(t)),$ med $0\leq t<\infty$ av rankade marknadsvikter

$\max _{1\leq i\leq n}\mu _{i}(t)=:\mu _{(1)}(t)\geq \mu _{(2)}(t) \geq \cdots \mu _{(n)}(t):=\min _{1\leq i\leq n}\mu _{i}(t)$

där band löses "lexikografiskt", alltid till förmån för det lägsta indexet. Logga luckorna

$G^{(k,k+1)}( t):=\log(\mu _{(k)}(t)/\mu _{(k+1)}(t)),$

där $0\leq t<\infty$ och $k=1,\dots ,n-1$ är kontinuerliga, icke-negativa semimartingales; vi betecknar med $\Lambda ^{(k,k+1)}(t)=L^{ G^{(k,k+1)}}(t;0)$ deras lokala tider vid ursprunget. Dessa kvantiteter mäter mängden omsättning mellan rangorden $k$ och $k+1$$\displaystyle [0,t]}$ tidsintervallet [ , .

En marknad kallas stokastiskt stabil , om $(\mu _{(1)}(t),\cdots ,\mu _{ (n)}(t))$ konvergerar i distribution som $t\rightarrow \infty$ till en slumpmässig vektor $(M_{(1) )},\cdots ,M_{(n)})$ med värden i Weyl-kammaren $\{(x_{1},\dots ,x_{n})\mid x_{1}>x_{2}>\dots >x_{n}{\text{ och }}\summa _ {i=1}^{n}x_{i}=1\}$ av enheten simplex, och om den starka lagen för stora tal

$\lim _{t\rightarrow \infty }{\frac {\Lambda ^{(k, k+1)}(t)}{t}}=\lambda ^{(k,k+1)}>0$

gäller för lämpliga reella konstanter $\lambda ^{(1,2)},\dots ,\lambda ^{(n-1,n)}.$

Arbitrage och numeraire egendom

Givet två valfria investeringsstrategier $\pi ,\rho$ och ett reellt tal $T>0$ , säger vi att $\pi$ är arbitrage relativt $\ rho$ över tidshorisonten $[0,T]$ , om $\mathbb {P} (Z_{\ pi }(T)\geq Z_{\rho }(T))\geq 1$ och $\mathbb {P} (Z_{\pi } (T)>Z_{\rho }(T))>0$ båda håller; detta relativa arbitrage kallas "starkt" om $\mathbb {P} (Z_{\pi }(T)>Z_{\rho }( T))=1.$ När $\rho$ är $\kappa \equiv 0,$ återställer vi den vanliga definitionen av arbitrage i förhållande till kontanter. Vi säger att en given strategi $\nu$ har numeräregenskapen , om för någon strategi $\pi$ förhållandet $Z_{\pi }/Z_{\nu }$ är en $\mathbb {P}$ −supermartingale. I ett sådant fall kallas processen ${\displaystyle 1/Z_{\nu }} en "deflator" för marknaden.$

Inget arbitrage är möjligt, över en given tidshorisont, relativt en strategi $\nu$ som har numeräregenskapen (antingen med avseende på det underliggande sannolikhetsmåttet $\mathbb {P}$ , eller med avseende på till något annat sannolikhetsmått som är ekvivalent med $\mathbb {P}$ ). En strategi $\nu$ med numeraire-egenskapen maximerar den asymptotiska tillväxthastigheten från investeringar, i den meningen att

$\limsup _{T\rightarrow \infty }{\frac {1}{T}}\log \left( {\frac {Z_{\pi }(T)}{Z_{\nu }(T)}}\right)\leq 0$

gäller för alla strategier $\pi$ ; det maximerar också den förväntade loggningsnyttan från investeringar, i den meningen att vi för alla strategier $\pi$ och reella tal $T>0$ har

$\mathbb {E} [\log(Z_{\pi }(T)]\leq \mathbb {E} [\log(Z_{\nu}(T))].$

Om vektorn $\alpha (t)=(\alpha _{1}(t),\cdots ,\alpha _ {n}(t))'$ av momentana avkastning, och matrisen $\sigma (t)=(\sigma (t) ))_{1\leq i,j\leq n}$ av momentana kovarianser, är kända, sedan strategin

$\nu (t)=\arg \max _ {p\in \mathbb {R} ^{n}}(p'\alpha (t)-{\tfrac {1}{2}}p'\alpha (t)p)\qquad {\text{ för alla }}0\leq t<\infty$

har numeräregenskapen närhelst det angivna maximumet uppnås.

Studien av numerärportföljen kopplar SPT till den så kallade Benchmark-metoden för Mathematical Finance, som tar en sådan numerärportfölj som given och ger ett sätt att prissätta villkorade anspråk, utan några ytterligare antaganden.

Ett sannolikhetsmått $\mathbb {Q}$ kallas ekvivalent martingalmått (EMM) på en given tidshorisont $\displaystyle [0,T]}$ , om det har samma nollmängder som $\mathbb {P}$ på ${\mathcal {F}}_{T}$ och om processerna $X_{ 1}(t),\dots ,X_{n}(t)$ med $0\leq t\leq T$ är alla $\mathbb {Q}$ −martingaler. Om man antar att ett sådant EMM existerar, är arbitrage inte möjligt på $[0,T]$ i förhållande till antingen kontanter $\kappa$ eller till marknadsportföljen $\mu$ (eller mer generellt, i förhållande till alla strategier $\rho$ vars välståndsprocess $Z_{\rho }$ är en martingal under vissa EMM). Omvänt, om $\pi ,\rho$ är portföljer och en av dem är arbitrage relativt den andra på $[0,T]$ så kan ingen EMM existera vid denna horisont.

Funktionellt genererade portföljer

Antag att vi får en jämn funktion $\displaystyle G:U\rightarrow (0,\infty )}$ på någon grannskap $U$ av enhetens simplex i $\ mathbb {R} ^{n}$ . Vi ringer

$\pi _{i}^{\mathbb {G} }(t):=\mu _{i}(t)\left(D_{i}\log (\mathbb {G} (\mu (t)))+1-\summa _{j=1}^{n}\mu _{j}(t)D_{j}\log(\mathbb {G} (\mu (t)))\right)\qquad {\text{ för }}1\leq i\leq n$

portföljen som genereras av funktionen $\mathbb {G}$ . Det kan visas att alla vikter i denna portfölj är icke-negativa, om dess genererande funktion $\mathbb {G}$ är konkav. Under milda förhållanden ges den relativa prestandan för denna funktionellt genererade portfölj $\pi _{\mathbb {G} }$ med avseende på marknadsportföljen $\mu$ , av FG-sönderdelningen

$\log \left( {\frac {Z_{\pi ^{\mathbb {G} }}(T)}{Z_{\mu }(T)}}\right)=\log \left({\frac {\mathbb {G} (\mu (T))}{\mathbb {G} (\mu (0))}}\right)+\int _{0}^{T}g(t)\,dt$

som inte innefattar några stokastiska integraler. Här är uttrycket

$g(t):={\frac {-1}{2\mathbb {G} (\mu (t))}}\summa _{i=1}^{n}\summa _{j=1}^{n}D_{ij}^{2}\mathbb {G} (\mu (t))\mu _{i}(t)\mu _{j}(t)\tau _{ij}^{\mu }(t)$

kallas portföljens driftprocess (och det är en icke-negativ storhet om genereringsfunktionen $\mathbb {G}$ är konkav); och kvantiteterna

$\tau _{ij}^{\mu }(t):=\summa _{\nu =1}^{n }(\xi _{i\nu}(t)-\xi _{\nu}^{\mu}(t))(\xi _{j\nu}(t)-\xi _{\nu} ^{\mu }(t)),\qquad \xi _{i\nu}(t):=\summa _{i=1}^{n}\mu _{i}(t)\xi _{ i\nu }(t)$

med $1\leq i,j\leq n$ kallas de relativa kovarianserna mellan $\log(X_{i})$ och $\log(X_{j})$ med avseende på marknaden.

Exempel

1. Konstantfunktionen $\mathbb {G} :=w>0$ genererar marknadsportföljen $\mu$ ,
2. Den geometriska medelfunktionen $\mathbb {H} (x):=(x_{1}\cdots x_{n})^{\frac {1 }{n}}$ genererar den likaviktade portföljen $\varphi _{i}(n)={\frac {1}{n}}$ för alla $1\leq i\leq n$ ,
3. Den modifierade entropifunktionen $\mathbb {S} ^{c}(x)=c-\summa _{i= 1}^{n}x_{i}\cdot \log(x_{i})$ för valfri $c>0$ genererar den modifierade entropivägda portföljen ,
4. Funktionen $\mathbb {D} ^{(p)}(x):=(\summa _{i=1 }^{n}x_{i}^{p})^{\frac {1}{p}}$ med $0<p<1$ genererar den mångfaldsvägda portföljen $\delta _{i}^{(p)}(t)={\frac {( \mu _{i}(t))^{p}}{\sum _{i=1}^{n}(\mu _{i}(t))^{p}}}$ med driftprocess $(1-p)\gamma _{\delta ^{(p)}}^{*}(t)$ .

Arbitrage i förhållande till marknaden

Den överskjutande tillväxttakten för marknadsportföljen medger representationen ${\displaystyle 2\gamma _{\mu }^{* }(t)=\summa _{i=1}^{n}\mu _{i}(t)\tau _{ii}^{\mu }(t)} som en kapitaliseringsvägd genomsnittlig relativ$ aktievariation . Denna kvantitet är icke-negativ; om den råkar vara avgränsad från noll, nämligen

$\gamma _{\mu }^{*}(t)={\ frac {1}{2}}\sum _{i=1}^{n}\mu _{i}(t)\tau _{ii}^{\mu }(t)\geq h>0,$

för alla $0\leq t<\infty$ för någon reell konstant $h$ , då kan det visas med FG-sönderdelningen att för varje $T>\mathbb {S} (\mu (0))/h,$ det finns en konstant $c>0$ för vilken den modifierade entropiska portföljen $\ Theta ^{(c)}$ är strikt arbitrage i förhållande till marknaden $\mu$ över $[0,T]$ ; se Fernholz och Karatzas (2005) för detaljer. Det är en öppen fråga om sådant arbitrage existerar över godtyckliga tidshorisonter (för två specialfall, där svaret på denna fråga visar sig vara jakande, se stycket nedan och nästa avsnitt).

Om egenvärdena för kovariansmatrisen $(\sigma _{ij}(t))_{1\leq i,j\leq n}$ är avgränsat från både noll och oändlighet kan villkoret $\gamma _{\mu }^{*}\geq h>0$ visas vara ekvivalent med diversitet, nämligen $\mu _{\max }\leq 1-\varepsilon$ för en lämplig $\varepsilon \in (0,1).$ Då leder den diversitetsvägda portföljen $\delta ^{(p)}$ till strikt arbitrage i förhållande till marknadsportföljen över tillräckligt långa tidshorisonter ; Lämpliga modifieringar av denna mångfaldsvägda portfölj realiserar ett sådant strikt arbitrage över godtyckliga tidshorisonter.

Ett exempel: volatilitetsstabiliserade marknader

Vi betraktar exemplet med ett system av stokastiska differentialekvationer

$d\log(X_{i}(t))={ \frac {\alpha }{2\mu _{i}(t)}}\,dt+{\frac {\sigma }{\mu _{i}(t)}}\,dW_{i}(t)$

med $1\leq i\leq n$ givna reella konstanter $\alpha \geq 0$ och en $n$ -dimensionell Brownsk rörelse $(W_{1},\dots ,W_{n}).$ Det följer av Bass och Perkins (2002) arbete att detta system har en svag lösning, som är unik i distributionen. Fernholz och Karatzas (2005) visar hur man konstruerar denna lösning i termer av skalade och tidsförändrade kvadratiska Bessel-processer , och bevisar att det resulterande systemet är koherent.

Det totala börsvärdet $X$ beter sig här som geometrisk Brownsk rörelse med drift och har samma konstanta tillväxttakt som den största aktien; medan den överskjutande tillväxttakten för marknadsportföljen är en positiv konstant. Å andra sidan har de relativa marknadsvikterna $\mu _{i}$ med $1\leq i\leq n$ dynamiken hos multiallel Wright-Fisher-processer . Denna modell är ett exempel på en icke-divers marknad med obegränsade varianser, där det finns starka arbitragemöjligheter med avseende på marknadsportföljen $\mu$ över godtyckliga tidshorisonter , vilket visades av Banner och Fernholz (2008). Dessutom härledde Pal (2012) den gemensamma tätheten av marknadsvikter vid fasta tider och vid vissa stopptider.

Rankbaserade portföljer

Vi fixar ett heltal $m\in \{2,\dots ,n-1\}$ och konstruerar två kapitalviktade portföljer: en som består av de översta ${\ displaystyle m}$ aktier, betecknade $\zeta$ , och en bestående av de nedre $nm$ aktierna, betecknade $\eta$ . Mer specifikt,

$\zeta _{i}(t)={\frac {\sum _{k=1}^{m}\mu _{(k)}(t)\mathbf {1} _{\{\mu _{ i}(t)=\mu _{(k)}(t)\}}}{\sum _{l=1}^{m}\mu _{(l)}(t)}}\qquad { \text{ och }}\eta _{i}(t)={\frac {\sum _{k=m+1}^{n}\mu _{(k)}(t)\mathbf {1} _{\{\mu _{i}(t)=\mu _{(k)}(t)\}}}{\summa _{l=m+1}^{n}\mu _{(l )}(t)}}$

för $1\leq i\leq n.$ Fernholz (1999), (2002) visade att den relativa utvecklingen för storaktieportföljen i förhållande till marknaden anges som

$\log \left({\frac {Z_{\zeta}(t)}{Z_{\mu }(t)}}\right)=\log \left({\frac {\mu _{( 1)}(T)+\cdots +\mu _{(m)}(T)}{\mu _{(1)}(0)+\cdots +\mu _{(m)}(0)} }\right)-{\frac {1}{2}}\int _{0}^{T}{\frac {\mu _{(m)}(t)}{\mu _{(1)} (t)+\cdots +\mu _{(m)}(t)}}\,d\Lambda ^{(m,m+1)}(t).$

Faktum är att om det inte finns någon omsättning på mth rang under intervallet ${\displaystyle [0,T]} bestäms$ förmögenheterna för $\zeta$ i förhållande till marknaden enbart på basis av hur den totala kapitaliseringen av detta underuniversum av de $m$ största aktiepriserna, vid tidpunkten $T$ kontra tid 0; Närhelst det är omsättning på ${\displaystyle m} -th rangen$ måste $\zeta$ dock sälja med förlust en aktie som blir "nedflyttad" till den lägre ligan och köpa en aktie som har stigit i värde och blivit befordrad. Detta står för "läckaget" som är uppenbart under den sista termen, en integral med avseende på den kumulativa omsättningsprocessen $\Lambda ^{(m,m+1)}$ av relativ vikt i storbolagsportföljen $\zeta$ av aktien som upptar mån.

Den omvända situationen råder med portföljen $\eta$ av småaktier, som får sälja med vinst aktier som flyttas upp till "upper capitalization"-ligan och köpa relativt billiga aktier som håller på att degraderas:

$\log \left({\frac {Z_{\eta }(t)}{Z_{\mu }(t)}}\right)=\log \left({\frac {\mu _{( m+1)}(T)+\cdots +\mu _{(n)}(T)}{\mu _{(m+1)}(0)+\cdots +\mu _{(n)} (0)}}\right)+{\frac {1}{2}}\int _{0}^{T}{\frac {\mu _{(m+1)}(t)}{\mu _{(m+1)}(t)+\cdots +\mu _{(n)}(t)}}.$

Det är tydligt från dessa två uttryck att, på en sammanhängande och stokastiskt stabil marknad, kommer den små aktiekapitalviktade portföljen $\zeta$ att tendera att överträffa sin motsvarighet för stora aktier $\eta$ , kl. åtminstone över stora tidshorisonter och; i synnerhet har vi under dessa förhållanden

$\lim _{T\rightarrow \infty }{\frac {1}{T}}\log \left({\ frac {Z_{\eta }(t)}{Z_{\mu }(t)}}\right)=\lambda ^{(m,m+1)}\mathbb {E} \left({\frac { M_{(1)}}{M_{(1)}+\cdots +M_{(m)}}}+{\frac {M_{(m+1)}}{M_{(m+1)}+ \cdots +M_{(n)}}}\right)>0.$

Detta kvantifierar den så kallade storlekseffekten . I Fernholz (1999, 2002) generaliseras konstruktioner som dessa till att inkludera funktionellt genererade portföljer baserade på rangordnade marknadsvikter.

Första och andra ordningens modeller

Första och andra ordningens modeller är hybrid Atlas-modeller som återger en del av strukturen på verkliga aktiemarknader. Första ordningens modeller har endast rankbaserade parametrar och andra ordningens modeller har både rankbaserade och namnbaserade parametrar.

Antag att $X_{1},\ldots ,X_{n}$ är en sammanhängande marknad och att gränserna

$\mathbf {\sigma } _{k}^{2}=\lim _{t\to \infty } t^{-1}\langle \log \mu _{(k)}\rangle (t)$

och

$\mathbf {g} _{k}=\lim _ {T\to \infty }{\frac {1}{T}}\int _{0}^{T}\sum _{i=1}^{n}\mathbf {1} _{\{r_{ t}(i)=k\}}\,d\log \mu _{i}(t)$

existerar för $k=1,\ldots ,n$ , där $r_{t}(i)$ är rangordningen för ${\ displaystil X_{i}(t)}$ . Sedan definieras Atlasmodellen ${\displaystyle {\widehat {X}}_{1},\ldots ,{\widehat {X}}_{n}} av$

$d\log {\widehat {X}}_{i}(t)=\sum _{k=1}^{n}\mathbf {g} _{k}\, \mathbf {1} _{\{{\hat {r}}_{t}(i)=k\}}\,dt+\sum _{k=1}^{n}\mathbf {\sigma } _ {k}\mathbf {1} _{\{{\hat {r}}_{t}(i)=k\}}\,dW_{i}(t),$

där ${\hat {r}}_{t}(i)$ är rangordningen för ${\widehat {X}}_{i}( t)$ och $(W_{1},\ldots ,W_{n})$ är en $n$ -dimensionell Brownsk rörelseprocess, är den första ordningens modell för den ursprungliga marknaden, $X_{1},\ldots ,X_{n}$ .

Under rimliga förhållanden kommer kapitalfördelningskurvan för en första ordningens modell att ligga nära den ursprungliga marknaden. En första ordningens modell är dock ergodisk i den meningen att varje aktie asymptotiskt spenderar $(1/n)$ -del av sin tid vid varje rang, en egenskap som inte finns på faktiska marknader. För att variera andelen tid som en aktie spenderar vid varje rankning är det nödvändigt att använda någon form av hybrid Atlas-modell med parametrar som beror på både rank och namn. Ett försök i denna riktning gjordes av Fernholz, Ichiba och Karatzas (2013), som introducerade en andra ordningens modell för marknaden med rank- och namnbaserade tillväxtparametrar och variansparametrar som enbart berodde på rank.

• Fernholz, ER (2002). Stokastisk portföljteori . New York: Springer-Verlag.