Sinusformad spiral

Sinusformade spiraler ( r ⁿ = –1 ⁿ cos( nθ ), θ = π /2 ) i polära koordinater och deras ekvivalenter i rektangulära koordinater :

   n = −2 : Liksidig hyperbel

   n = −1 : Linje

   n = −1/2 : Parabel

   n = 1/2 : Kardioid

   n = 1 : Cirkel

   n = 2 : Lemniscate of Bernoulli

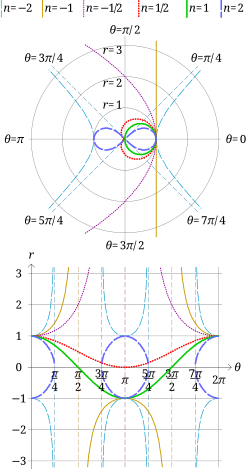
I algebraisk geometri är de sinusformade spiralerna en familj av kurvor som definieras av ekvationen i polära koordinater

$r^{n}=a^{n}\cos(n\theta )\,$

där a är en konstant som inte är noll och n är ett annat rationellt tal än 0. Med en rotation kring origo kan detta också skrivas

$r^{n}=a^{n}\sin(n\theta ).\,$

Termen "spiral" är en felaktig benämning, eftersom de inte är faktiskt spiraler , och ofta har en blomliknande form. Många välkända kurvor är sinusformade spiraler inklusive:

• Rektangulär hyperbel ( n = −2 )
• Linje ( n = −1 )
• Parabel ( n = −1/2 )
• Tschirnhausen kubisk ( n = −1/3 )
• Cayleys sextett ( n = 1/3 )
• Kardioid ( n = 1/2 )
• Cirkel ( n = 1 )
• Lemniscate of Bernoulli ( n = 2 )

Kurvorna studerades först av Colin Maclaurin .

Ekvationer

Differentiera

$r^{n}=a^{n}\cos(n\theta )\,$

och eliminering av a ger en differentialekvation för r och θ:

${\frac {dr}{d\theta }}\cos n\theta +r\sin n\theta =0$ .

Sedan

$_ \displaystyle \left({\frac {dr}{ds}},\ r{\frac {d\theta }{ds}}\right)\cos n\theta {\frac {ds}{d\theta }} =\left(-r\sin n\theta ,\ r\cos n\theta \right)=r\left(-\sin n\theta ,\ \cos n\theta \right)}$

vilket innebär att den polära tangentiella vinkeln är

$\psi =n\theta \pm \pi /2$

och så är den tangentiella vinkeln

$\varphi =(n+1)\theta \pm \pi /2$ .

(Tecknet här är positivt om r och cos n θ har samma tecken och negativt annars.)

Enhetstangensvektorn,

$\left({\frac {dr}{ds}},\ r{\frac {d\theta }{ds}}\right)$ ,

har längd ett, så att jämföra storleken på vektorerna på varje sida av ovanstående ekvation ger

${\frac {ds}{d\theta }}=r\cos ^{-1}n\theta =a\cos ^{-1+{\tfrac {1}{n}}}n\theta$ .

är längden på en enda slinga när ${\displaystyle n>0} :$

$a\int _{-{\tfrac {\pi }{2n}}}^{\tfrac {\pi }{ 2n}}\cos ^{-1+{\tfrac {1}{n}}}n\theta \ d\theta$

Krökningen ges av

${\frac {d\varphi }{ds}}=(n+1){\ frac {d\theta }{ds}}={\frac {n+1}{a}}\cos ^{1-{\tfrac {1}{n}}}n\theta$ .

Egenskaper

Inversen av en sinusformad spiral med avseende på en cirkel med centrum i origo är en annan sinusformad spiral vars värde på n är det negativa av den ursprungliga kurvans värde på n . Till exempel är inversen av Bernoullis lemniscate en rektangulär hyperbel.

Den isoptiska , pedalen och negativa pedalen i en sinusformad spiral är olika sinusformade spiraler.

En bana för en partikel som rör sig enligt en central kraft som är proportionell mot styrkan r är en sinusformad spiral.

När n är ett heltal och n punkter är ordnade regelbundet på en cirkel med radien a , då är uppsättningen punkter så att det geometriska medelvärdet av avstånden från punkten till n punkter är en sinusformad spiral. I detta fall är den sinusformade spiralen ett polynomiskt lemniscat .

• Yates, RC: A Handbook on Curves and Their Properties , JW Edwards (1952), "Spiral" sid. 213–214
• "Sinusformad spiral" på www.2dcurves.com
• "Sinusformade spiraler" på The MacTutor History of Mathematics
• Weisstein, Eric W. "Sinusformad spiral" . MathWorld .