Shrikhande graf

Shrikhande-grafen
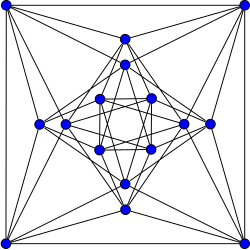Shrikhande-grafen
	Shrikhande-grafen
Döpt efter	SS Shrikhande
Vertices	16
Kanter	48
Radie	2
Diameter	2
Omkrets	3
Automorfismer	192
Kromatiskt nummer	4
Kromatiskt index	6
Boktjocklek	4
Könummer	3
Egenskaper	; ; ; ; Starkt regelbunden Hamiltonsymmetrisk Eulerisk integral
	Tabell över grafer och parametrar

Inom det matematiska området för grafteorin är Shrikhande-grafen en namngiven graf som upptäcktes av SS Shrikhande 1959. Det är en starkt regelbunden graf med 16 hörn och 48 kanter , där varje vertex har grad 6. Varje nodpar har exakt två andra noder grannar gemensamt, oavsett om nodparet är anslutet eller inte.

Konstruktion

Shrikhande-grafen kan konstrueras som en Cayley-graf . Hönsmängden är $\mathbb {Z} _{4}\times \mathbb {Z} _{4}$ . Två hörn är intilliggande om och endast om skillnaden är i $\{\pm (1,0),\pm (0, 1),\pm (1,1)\}$ .

Egenskaper

I Shrikhande-grafen har alla två hörn I och J två distinkta grannar gemensamma (exklusive de två hörnen I och J själva), vilket gäller oavsett om I är intill J eller inte . Med andra ord, den är starkt regelbunden och dess parametrar är: {16,6,2,2}, dvs $\lambda =\mu =2$ . Denna likhet innebär att grafen är associerad med en symmetrisk BIBD . Shrikhande-grafen delar dessa parametrar med exakt en annan graf, 4×4- tornets graf , dvs linjegrafen L ( K 4,4 ₎ för den kompletta tvådelade grafen K _4,4 . Den senare grafen är den enda linjegrafen L ( K _n,n ) för vilken de starka regularitetsparametrarna inte bestämmer den grafen unikt utan delas med en annan graf, nämligen Shrikhande-grafen (som inte är en tornsgraf).

Shrikhande-grafen är lokalt hexagonal ; det vill säga grannarna till varje hörn bildar en cykel av sex hörn. Som med vilken lokalt cyklisk graf som helst, är Shrikhande-grafen 1-skelettet av en Whitney-triangulering av någon yta; i fallet med Shrikhande-grafen är denna yta en torus där varje vertex omges av sex trianglar. Således är Shrikhande-grafen en toroidformad graf . Inbäddningen bildar en vanlig karta i torus, med 32 triangulära ytor. Skelettet av dualen av denna karta (som inbäddad i torusen) är Dyck-grafen , en kubisk symmetrisk graf.

Shrikhande-grafen är inte en distanstransitiv graf . Det är den minsta avstånds-reguljära grafen som inte är avståndstransitiv.

Automorfismgruppen i Shrikhande-grafen är av ordningen 192. Den verkar transitivt på hörnen , på kanterna och på grafens bågar. Därför är Shrikhande-grafen en symmetrisk graf .

Det karakteristiska polynomet för Shrikhande-grafen är: $(x-6)(x-2)^{6}(x+2)^{ 9}$ . Därför är Shrikhande-grafen en integrerad graf : dess spektrum består helt av heltal.