Inom kinematik definieras rörelsen hos en stel kropp som en kontinuerlig uppsättning förskjutningar. Enparameterrörelser kan definieras som en kontinuerlig förskjutning av ett rörligt föremål med avseende på en fast ram i euklidiskt trerum ( E 3 ), där förskjutningen beror på en parameter, mestadels identifierad som tid.
Rationella rörelser definieras av rationella funktioner (förhållandet mellan två polynomfunktioner ) av tiden. De producerar rationella banor , och därför integreras de väl med de befintliga NURBS (Non-Uniform Rational B-Spline) baserade industristandard CAD/CAM - systemen. De är lätt tillgängliga för tillämpningar av befintliga datorstödda geometriska design ( CAGD) algoritmer. Genom att kombinera kinematik av stela kroppsrörelser med NURBS-geometri av kurvor och ytor , har metoder utvecklats för datorstödd design av rationella rörelser.
Dessa CAD-metoder för rörelsedesign hittar tillämpningar inom animering i datorgrafik (nyckelramsinterpolation ) , banaplanering inom robotik (inlärt positionsinterpolation), rumslig navigering i virtuell verklighet , datorstödd geometrisk design av rörelse via interaktiv interpolation, CNC- verktygsbana planering och uppgiftsspecifikation i mekanismsyntes .
Bakgrund
Det har gjorts en hel del forskning för att tillämpa principerna för datorstödd geometrisk design (CAGD) på problemet med datorstödd rörelsedesign. Under de senaste åren har det varit väl etablerat att rationella Bézier- och rationella B-spline- baserade kurvrepresentationsscheman kan kombineras med dubbelkvarternionrepresentation av rumsliga förskjutningar för att erhålla rationella Bézier- och B-spline-rörelser. Ge och Ravani, utvecklade ett nytt ramverk för geometriska konstruktioner av rumsliga rörelser genom att kombinera koncepten från kinematik och CAGD. Deras arbete byggdes på Shoemakes banbrytande papper, där han använde begreppet en quaternion för rotationsinterpolation . En detaljerad lista med referenser om detta ämne finns i och.
Rationella Bézier- och B-spline-rörelser
Låt  quaternion . En homogen dubbelkvarternion kan skrivas som ett par kvartjoner,
quaternion . En homogen dubbelkvarternion kan skrivas som ett par kvartjoner,  ; där
; där  . Detta erhålls genom att expandera
. Detta erhålls genom att expandera  } med dubbeltalsalgebra (här,
} med dubbeltalsalgebra (här,  .
.
När det gäller dubbla kvaternioner och de homogena koordinaterna för en punkt  för objektet ges transformationsekvationen i termer av kvaternioner av
för objektet ges transformationsekvationen i termer av kvaternioner av
![{\displaystyle {\tilde {\textbf {P}}}={\textbf {Q}}{\textbf {P}}{\textbf {Q}}^{\ast }+P_{4}[({\textbf {Q}}^{0}){\textbf {Q}}^{\ast }-{\textbf {Q}}({\textbf {Q}}^{0})^{\ast }],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7faf11b42265af9cb44b88f632530a3b7e0a9a95) Q
Q  och
och  är konjugat av
är konjugat av  och
och  , respektive
, respektive  betecknar homogena koordinater för punkten efter förskjutningen.
betecknar homogena koordinater för punkten efter förskjutningen.
Givet en uppsättning enhetsdubbla kvaternioner och dubbla vikter  följande representerar en rationell Bézier-kurva i utrymmet för dubbla kvaternioner.
följande representerar en rationell Bézier-kurva i utrymmet för dubbla kvaternioner.

där  är Bernstein-polynomen. Béziers dubbla kvaternionkurva som ges av ovanstående ekvation definierar en rationell Bézier-rörelse av grad
är Bernstein-polynomen. Béziers dubbla kvaternionkurva som ges av ovanstående ekvation definierar en rationell Bézier-rörelse av grad  .
.
På liknande sätt ges en B-spline dubbel kvaternionkurva, som definierar en NURBS-rörelse av grad 2 p , av,

där  basfunktionerna i p :te graders B-spline.
basfunktionerna i p :te graders B-spline.
En representation för den rationella Bézier-rörelsen och den rationella B-spline-rörelsen i det kartesiska rymden kan erhållas genom att ersätta något av de två föregående uttrycken ovan för  i ekvationen för punkttransform. I det följande behandlar vi fallet med rationell Bézier-rörelse. Banan för en punkt som genomgår rationell Bézier-rörelse ges av,
i ekvationen för punkttransform. I det följande behandlar vi fallet med rationell Bézier-rörelse. Banan för en punkt som genomgår rationell Bézier-rörelse ges av,
![{\displaystyle {\tilde {\textbf {P}}}^{2n}(t)=[H^{2n}(t)]{\textbf {P}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a3ac5a5cf28652fb260c22b3bfc325adb6f3554)
![{\displaystyle H^{2n}(t)]=\sum \limits _{k=0}^{2n}{B_{k}^{2n}(t)[H_{k}]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a07b7741b8732cfeacff62b64bce278fdf4940a)
där ![{\displaystyle [H^{2n}(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff007669205daa95623361d7f9dd684be89ede51) är matrisrepresentationen av den rationella Bézier-rörelsen av grad
är matrisrepresentationen av den rationella Bézier-rörelsen av grad  i det kartesiska rymden. Följande matriser
i det kartesiska rymden. Följande matriser ![{\displaystyle [H_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/445d98cb219e5a63aa2a0c68a7f3ae24f954f875) (även kallade Bézier Control Matrices) definierar den affina kontrollstrukturen för rörelsen:
(även kallade Bézier Control Matrices) definierar den affina kontrollstrukturen för rörelsen:
![{\displaystyle [H_{k}]={\frac {1}{C_{k}^{2n}}}\sum \limits _{i+j=k}{C_{i}^{n}C_{j}^{n}w_{i}w_{j}[H_{ij}^{\ast }]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21caa074cd4c478a663effafed481b451d5b94c8)
där ![{\displaystyle [H_{ij}^{\ast }]=[H_{i}^{+}][H_{j}^{-}]+[H_{j}^{-}][H_{i}^{0+}]-[H_{i}^{+}][H_{j}^{0-}]+(\alpha _{i}-\alpha _{j})[H_{j}^{-}][Q_{i}^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40b7989aa4496f625f3d58fbe6cbea28f1b2684a) .
.
I ovanstående ekvationer är  och
och  binomialkoefficienter och
binomialkoefficienter och  är viktförhållandena och
är viktförhållandena och
![{\displaystyle [H_{j}^{-}]=\left[{\begin{array}{rrrr}q_{j,4}&-q_{j,3}&q_{j,2}&-q_{j,1}\\q_{j,3}&q_{j,4}&-q_{j,1}&-q_{j,2}\\-q_{j,2}&q_{j,1}&q_{j,4}&-q_{j,3}\\q_{j,1}&q_{j,2}&q_{j,3}&q_{j,4}\\\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0786e905608c0547a22d8887bc0545aca68bfe21)
![{\displaystyle [Q_{i}^{+}]=\left[{\begin{array}{rrrr}0&0&0&q_{i,1}\\0&0&0&q_{i,2}\\0&0&0&q_{i,3}\\0&0&0&q_{i,4}\\\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e046ae22366c88f34f432b175bac827a57dac6d0)
![{\displaystyle [H_{i}^{0+}]=\left[{\begin{array}{rrrr}0&0&0&q_{i,1}^{0}\\0&0&0&q_{i,2}^{0}\\0&0&0&q_{i,3}^{0}\\0&0&0&q_{i,4}^{0}\\\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4159d3f64a6b198f3274c8787e6ec1a91fd2cc19)
![{\displaystyle [H_{j}^{0-}]=\left[{\begin{array}{rrrr}0&0&0&-q_{j,1}^{0}\\0&0&0&-q_{j,2}^{0}\\0&0&0&-q_{j,3}^{0}\\0&0&0&q_{j,4}^{0}\\\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ea89eeecca2fda1fe1bfedc24d5edd6845924b0)
![{\displaystyle [H_{i}^{+}]=\left[{\begin{array}{rrrr}q_{i,4}&-q_{i,3}&q_{i,2}&q_{i,1}\\q_{i,3}&q_{i,4}&-q_{i,1}&q_{i,2}\\-q_{i,2}&q_{i,1}&q_{i,4}&q_{i,3}\\-q_{i,1}&-q_{i,2}&-q_{i,3}&q_{i,4}\\\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f7b0b2c46b4ae523f8fd8a77474007ae913c087)
I ovanstående matriser,  är fyra komponenter i den reella delen
är fyra komponenter i den reella delen  och
och  är fyra komponenter i den dubbla delen
är fyra komponenter i den dubbla delen  av enheten dual quaternion
av enheten dual quaternion  .
.
Exempel
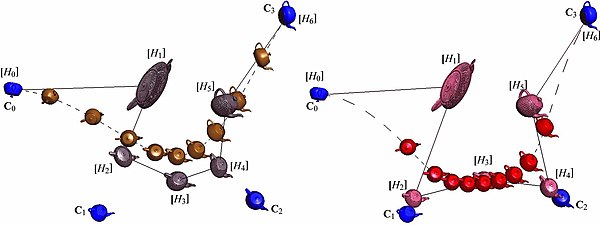
En tekanna under Rational Bézier-rörelse av grad 6 med (till vänster) enhetsverkliga vikter (

) (till höger) reella vikter som inte är enhetliga (

och

); visas också affina positioner (förvrängda) samt de givna kontrollpositionerna (i blå färg).
Se även
externa länkar






![{\displaystyle {\tilde {\textbf {P}}}={\textbf {Q}}{\textbf {P}}{\textbf {Q}}^{\ast }+P_{4}[({\textbf {Q}}^{0}){\textbf {Q}}^{\ast }-{\textbf {Q}}({\textbf {Q}}^{0})^{\ast }],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7faf11b42265af9cb44b88f632530a3b7e0a9a95)












![{\displaystyle {\tilde {\textbf {P}}}^{2n}(t)=[H^{2n}(t)]{\textbf {P}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a3ac5a5cf28652fb260c22b3bfc325adb6f3554)
![{\displaystyle H^{2n}(t)]=\sum \limits _{k=0}^{2n}{B_{k}^{2n}(t)[H_{k}]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a07b7741b8732cfeacff62b64bce278fdf4940a)
![{\displaystyle [H^{2n}(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff007669205daa95623361d7f9dd684be89ede51)
![{\displaystyle [H_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/445d98cb219e5a63aa2a0c68a7f3ae24f954f875)
![{\displaystyle [H_{k}]={\frac {1}{C_{k}^{2n}}}\sum \limits _{i+j=k}{C_{i}^{n}C_{j}^{n}w_{i}w_{j}[H_{ij}^{\ast }]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21caa074cd4c478a663effafed481b451d5b94c8)
![{\displaystyle [H_{ij}^{\ast }]=[H_{i}^{+}][H_{j}^{-}]+[H_{j}^{-}][H_{i}^{0+}]-[H_{i}^{+}][H_{j}^{0-}]+(\alpha _{i}-\alpha _{j})[H_{j}^{-}][Q_{i}^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40b7989aa4496f625f3d58fbe6cbea28f1b2684a)



![{\displaystyle [H_{j}^{-}]=\left[{\begin{array}{rrrr}q_{j,4}&-q_{j,3}&q_{j,2}&-q_{j,1}\\q_{j,3}&q_{j,4}&-q_{j,1}&-q_{j,2}\\-q_{j,2}&q_{j,1}&q_{j,4}&-q_{j,3}\\q_{j,1}&q_{j,2}&q_{j,3}&q_{j,4}\\\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0786e905608c0547a22d8887bc0545aca68bfe21)
![{\displaystyle [Q_{i}^{+}]=\left[{\begin{array}{rrrr}0&0&0&q_{i,1}\\0&0&0&q_{i,2}\\0&0&0&q_{i,3}\\0&0&0&q_{i,4}\\\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e046ae22366c88f34f432b175bac827a57dac6d0)
![{\displaystyle [H_{i}^{0+}]=\left[{\begin{array}{rrrr}0&0&0&q_{i,1}^{0}\\0&0&0&q_{i,2}^{0}\\0&0&0&q_{i,3}^{0}\\0&0&0&q_{i,4}^{0}\\\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4159d3f64a6b198f3274c8787e6ec1a91fd2cc19)
![{\displaystyle [H_{j}^{0-}]=\left[{\begin{array}{rrrr}0&0&0&-q_{j,1}^{0}\\0&0&0&-q_{j,2}^{0}\\0&0&0&-q_{j,3}^{0}\\0&0&0&q_{j,4}^{0}\\\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ea89eeecca2fda1fe1bfedc24d5edd6845924b0)
![{\displaystyle [H_{i}^{+}]=\left[{\begin{array}{rrrr}q_{i,4}&-q_{i,3}&q_{i,2}&q_{i,1}\\q_{i,3}&q_{i,4}&-q_{i,1}&q_{i,2}\\-q_{i,2}&q_{i,1}&q_{i,4}&q_{i,3}\\-q_{i,1}&-q_{i,2}&-q_{i,3}&q_{i,4}\\\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f7b0b2c46b4ae523f8fd8a77474007ae913c087)








