Quantum värmemotorer och kylskåp

En kvantvärmemotor är en anordning som genererar kraft från värmeflödet mellan varma och kalla reservoarer. Motorns funktionsmekanism kan beskrivas av kvantmekanikens lagar . Den första realiseringen av en kvantvärmemotor påpekades av Scovil och Schulz-DuBois 1959, vilket visar kopplingen mellan effektiviteten mellan Carnot -motorn och 3- nivåmasern . Quantum- kylskåp delar strukturen hos kvantvärmemotorer med syftet att pumpa värme från ett kallt till ett varmt bad som förbrukar ström som först föreslogs av Geusic, Schulz-DuBois, De Grasse och Scovil. När strömmen tillförs av en laser kallas processen för optisk pumpning eller laserkylning , vilket föreslås av Wineland och Hänsch . Överraskande nog värmemotorer och kylskåp fungera upp till skalan av en enda partikel, vilket motiverar behovet av en kvantteori som kallas kvanttermodynamik .

3-nivåförstärkaren som en kvantvärmemotor

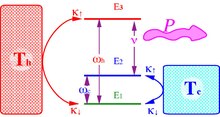
Trenivåförstärkaren. Nivå 1 och 3 är kopplade till den heta behållaren. Nivå 1 och 2 är kopplade till den kalla reservoaren. Effekt erhålls när det är populationsinversion mellan nivå 3 och 2.

Trenivåförstärkaren är mallen för en kvantenhet. Den fungerar genom att använda ett varmt och kallt bad för att upprätthålla populationsinversion mellan två energinivåer som används för att förstärka ljus genom stimulerad emission. Grundtillståndsnivån ( 1-g ) och den exciterade nivån ( 3-h ) kopplas till ett varmt bad av temperaturen $T_{\text{h}}$ . Energigapet är $\hbar \omega _{\text{h}}=E_{3}-E_{1}$ . När befolkningen på nivåerna utjämnar sig

${\frac {N_{\text{h}}}{N_{\text{g}}}}=e^{-{\frac { \hbar \omega _{\text{h}}}{k_{\text{B}}T_{\text{h}}}}}$

där $\hbar ={\frac {h}{2\pi }}$ är Planck-konstanten och $k_{\text{B}}$ är Boltzmann-konstanten . Det kalla badet med temperaturen $T_{\text{c}}$ kopplar marken ( 1-g ) till en mellannivå ( 2-c ) med energigap ${\ displaystyle E_{2}-E_{1}=\hbar \omega _{\text{c}}}$ . När nivåerna 2-c och 1-g kommer i jämvikt

${\frac {N_{\text{c}}}{N_{\text{g}}}}=e^{-{\frac { \hbar \omega _{\text{c}}}{k_{\text{B}}T_{\text{c}}}}}$ .

Enheten fungerar som en förstärkare när nivåerna ( 3-h ) och ( 2-c ) är kopplade till ett externt frekvensfält $\nu$ . För optimala resonansförhållanden $\nu =\omega _{\text{h}}-\omega _{\text{c}}$ . Effektiviteten hos förstärkaren vid omvandling av värme till effekt är förhållandet mellan arbetseffekt och värmetillförsel:

$\eta ={\frac {\hbar \nu }{\hbar \omega _{\text{h}}}}=1-{\frac {\omega _{\text{c}}}{\omega _{\text{h}}}}$ .

Förstärkning av fältet är endast möjlig för positiv förstärkning (populationsinversion) $G=N_{\text{h}}-N_{\text{c}}\geq 0$ . Detta motsvarar ${\frac {\hbar \omega _{\text{c}}}{k_{\text{B}}T_{ \text{c}}}}\geq {\frac {\hbar \omega _{\text{h}}}{k_{\text{B}}T_{\text{h}}}}$ . Att infoga detta uttryck i effektivitetsformeln leder till:

$\eta =1-{\frac {\omega _{\text{c}}}{\omega _{\text{h }}}}\leq 1-{\frac {T_{\text{c}}}{T_{\text{h}}}}=\eta _{\text{c}}$

där $\eta _{\text{c}}$ är Carnot-cykelns effektivitet . Likhet erhålls under ett nollförstärkningsvillkor $G=0$ . Relationen mellan kvantförstärkaren och Carnot -effektiviteten påpekades först av Scovil och Schultz-DuBois:

Att vända driften av att driva värme från det kalla badet till det varma badet genom att förbruka ström utgör ett kylskåp . Kylskåpets effektivitet definierad som prestandakoefficienten (COP) för den omvända enheten är:

$\epsilon ={\frac {\omega _{\text{c}}}{\nu }}\leq {\frac {T_{\text{ c}}}{T_{\text{h}}-T_{\text{c}}}}$

Typer

Quantum-enheter kan arbeta antingen kontinuerligt eller genom en fram- och återgående cykel. Kontinuerliga enheter inkluderar solceller som omvandlar solstrålning till elektrisk kraft, termoelektriska där uteffekten är ström och lasrar där uteffekten är koherent ljus. Det primära exemplet på ett kontinuerligt kylskåp är optisk pumpning och laserkylning . I likhet med klassiska kolvmotorer har kvantvärmemotorer också en cykel som är uppdelad i olika slag. Ett slag är ett tidssegment där en viss operation äger rum (t.ex. termalisering eller arbetsextraktion). Två intilliggande slag pendlar inte med varandra. De vanligaste fram- och återgående värmemaskinerna är fyrtaktsmaskinen och tvåtaktsmaskinen. Fram- och återgående anordningar har föreslagits att fungera antingen med Carnot-cykeln eller Otto-cykeln .

I båda typerna tillåter kvantbeskrivningen att erhålla rörelseekvationen för arbetsmediet och värmeflödet från reservoarerna.

Quantum fram- och återgående värmemotor och kylskåp

Se även: Kolvvärmemotor

Kvantversioner av de flesta av de vanliga termodynamiska cyklerna har studerats, till exempel Carnot-cykeln , Stirling-cykeln och Otto-cykeln .

Otto-cykeln kan fungera som mall för andra fram- och återgående cykler.

Kvant Otto-cykeln visas i Entropi $\Omega$ -planet där energientropin och Von Neumann-entropin visas. $\Omega$ är enhetens interna frekvens och styrs externt. Den efterliknar den omvända volymen i Otto-cykeln . De röda och blå linjerna är de varma och kalla isokorerna. Cykeln representerar en värmepump.

Den är sammansatt av följande fyra segment:

• Segment $A\rightarrow B$ isomagnetisk eller isokorisk process , partiell jämvikt med kallbadet under konstant Hamiltonian. Arbetsmediets dynamik kännetecknas av propagatorn ${U}/$ .
• Segment $B\rightarrow C$ magnetisering eller adiabatisk kompression , förändringar i det yttre fältet utökar gapet mellan energinivåerna hos Hamiltonian. Dynamiken kännetecknas av propagatorn ${U}_{\text{ch}}$ .
• Segment $C\rightarrow D$ isomagnetisk , eller isokorisk processpartiell jämvikt med det varma badet som beskrivs av propagatorn $U_{\text{h}}$ .
• Segment $D\rightarrow A$ avmagnetisering eller adiabatisk expansion som minskar energigaperna i Hamiltonian, kännetecknad av propagatorn $U_{\text{hc}}$ .

Utbredaren för fyrtaktscykeln blir ${\displaystyle U_{\text{global}}} ,$ som är den ordnade produkten av segmentpropagatorerna:

${U}_{\text{global}}~~=~~{U}_{\text{hc}}{U}_{\text{h }}{U}_{\text{ch}}{U}_{\text{c}}$

Propagatorerna är linjära operatorer definierade på ett vektorrum som helt bestämmer arbetsmediets tillstånd. Gemensamt för alla termodynamiska cykler pendlar inte de konsekutiva segmentutbredningarna $[{\ U}_{i},{U}_{j}]\neq 0$ . Pendlingspropagatorer kommer att leda till noll effekt.

I en fram- och återgående kvantvärmemotor är arbetsmediet ett kvantsystem såsom spinnsystem eller en harmonisk oscillator. För maximal effekt bör cykeltiden optimeras. Det finns två grundläggande tidsskalor i det fram- och återgående kylskåpet, cykeltiden $\tau _{\text{cyc}}$ och den interna tidsskalan $2\pi /\omega$ . I allmänhet när $\tau _{\text{cyc}}\gg 2\pi /\omega$ arbetar motorn i kvasi-adiabatiska förhållanden. Den enda kvanteffekten kan hittas vid låga temperaturer där enhetens energienhet blir $\hbar \omega$ istället för $k_{\text{B}}T$ . Effektiviteten vid denna gräns är $\eta =1-{\frac {\omega _{\text{c}}}{\omega _{\text{h}}}}$ , alltid mindre än Carnot-effektiviteten $\eta _{\text{c}}$ . Vid hög temperatur och för det harmoniska arbetsmediet blir verkningsgraden vid maximal effekt $\eta =1-{\sqrt {\frac {T_{\text{c}}}{T_{ \text{h}}}}}$ som är det endoversibla termodynamiska resultatet.

För kortare cykeltider kan arbetsmediet inte följa adiabatiskt förändringen av den externa parametern. Detta leder till friktionsliknande fenomen. Extra kraft krävs för att driva systemet snabbare. Signaturen för sådan dynamik är utvecklingen av koherens som orsakar extra förlust. Överraskande nog är dynamiken som leder till friktion kvantiserad, vilket innebär att friktionsfria lösningar på den adiabatiska expansionen /kompressionen kan hittas på ändlig tid. Som ett resultat måste optimering endast utföras med hänsyn till den tid som allokeras till värmetransport. I denna regim försämrar kvantfunktionen av koherens prestandan. Optimal friktionsfri prestanda erhålls när koherensen kan upphävas.

De kortaste cykeltiderna $\tau _{\text{cyc}}\ll 2\pi /\omega$ , ibland kallade plötsliga cykler, har universella egenskaper. I det här fallet bidrar koherens till cyklernas kraft.

En tvåtaktsmotorkvantcykel ekvivalent med Otto-cykeln baserad på två kvantbitar har föreslagits. Den första qubiten har frekvensen $\omega _{\text{h}}$ och den andra $\omega _{\text{c}}$ . Cykeln består av ett första slag av partiell utjämning av de två qubitarna med det varma och kalla badet parallellt. Det andra kraftslaget består av ett partiellt eller helt utbyte mellan qubitarna. Växlingsoperationen genereras av en enhetlig transformation som bevarar entropin som ett resultat av att det är ett rent kraftslag.

Kylskåpen med quantum Otto-cykeln delar samma cykel med magnetisk kylning .

Kontinuerliga kvantmotorer

Kontinuerliga kvantmotorer är kvantanalogerna av turbiner . Arbetsutgångsmekanismen är koppling till ett externt periodiskt fält, typiskt det elektromagnetiska fältet. Således värmemotorn en modell för en laser . Modellerna skiljer sig åt genom val av arbetssubstans och värmekälla och diskbänk. Externt drivna två-nivå, tre nivå fyra-nivå och kopplade harmoniska oscillatorer har studerats.

Den periodiska körningen delar upp arbetsmediets energinivåstruktur. Denna uppdelning gör att motorn med två nivåer kan kopplas selektivt till de varma och kalla baden och producera kraft. Å andra sidan, att ignorera denna uppdelning i härledningen av rörelseekvationen kommer att bryta mot termodynamikens andra lag .

Icke-termiska bränslen har övervägts för kvantvärmemotorer. Tanken är att öka energiinnehållet i det varma badet utan att öka dess entropi. Detta kan uppnås genom att använda koherens eller ett sammanpressat termiskt bad. Dessa enheter bryter inte mot termodynamikens andra lag.

Likvärdighet mellan fram- och återgående och kontinuerliga värmemaskiner i kvantregimen

Tvåtakts-, fyrtakts- och kontinuerlig maskin skiljer sig mycket från varandra. Det visades dock att det finns en kvantregim där alla dessa maskiner blir termodynamiskt ekvivalenta med varandra. Medan dynamiken inom cykeln i ekvivalensregimen är mycket olika för olika motortyper, visar sig när cykeln är klar alla ge samma mängd arbete och förbruka samma mängd värme (därav de delar samma effektivitet också) . Denna ekvivalens är associerad med en sammanhängande arbetsextraktionsmekanism och har ingen klassisk analog. Dessa kvantfunktioner har demonstrerats experimentellt.

Värmemotorer och öppna kvantsystem

Det elementära exemplet fungerar under kvasi-jämviktsförhållanden. Dess huvudsakliga kvantfunktion är den diskreta energinivåstrukturen. Mer realistiska enheter fungerar utanför jämvikt med friktionsvärmeläckor och ändligt värmeflöde. Kvanttermodynamik tillhandahåller en dynamisk teori som krävs för system utanför jämvikt, såsom värmemotorer, och infogar alltså dynamik i termodynamiken. Teorin om öppna kvantsystem utgör grundteorin. För värmemotorer eftersträvas en reducerad beskrivning av det arbetande ämnets dynamik, som spårar de varma och kalla baden. Utgångspunkten är den allmänna Hamiltonian för de kombinerade systemen:

$H=H_{\text{s}}s+H_{\text{c}}+H_{\text{h}} {\text{h}}+H_{\text{sc}}+H_{\text{sh}}$

och systemet Hamiltonian $H_{\text{s}}(t)$ är tidsberoende. En reducerad beskrivning leder till systemets rörelseekvation:

${\frac {d}{dt}}\rho =-{\frac {i}{ \hbar }}[H_{\text{s}},\rho ]+L_{\text{h}}(\rho )+L_{\text{c}}(\rho )$

där $\rho$ är densitetsoperatorn som beskriver arbetsmediets tillstånd och $L_{\text{h/c}}$ är generatorn av dissipativ dynamik som inkluderar termerna för värmetransport från baden. Med denna konstruktion blir den totala energiförändringen i delsystemet:

${\frac {d}{dt}}E=\left\langle { \frac {\partial H_{\text{s}}}{\partial t}}\right\rangle +\langle L_{\text{h}}(H_{\text{s}})\rangle +\langle L_{\text{c}}(H_{\text{s}})\rangle$

leder till den dynamiska versionen av termodynamikens första lag :

• Potensen $P=\left\langle {\frac {\partial H}{\partial t}}\right\rangle$
• Värmeströmmar $J_{\text{h}}=\langle L_{\text{h}}(H_{\text{s}})\rangle$ och $J_{\text{c}}=\langle L_{\text{c}}(H_{\text{s}})\rangle$ .

Entropiproduktionshastigheten blir :

${\frac {dS}{dt}}=-{\frac {J_{\text{h}}}{T_{\text{ h}}}}-{\frac {J_{\text{c}}}{T_{\text{c}}}}\geq 0$

Kvantmekanikens globala struktur återspeglas i härledningen av den reducerade beskrivningen. En härledning som är förenlig med termodynamikens lagar är baserad på den svaga kopplingsgränsen. En termodynamisk idealisering förutsätter att systemet och baden är okorrelerade, vilket innebär att det totala tillståndet för det kombinerade systemet alltid blir en tensorprodukt:

$\rho =\rho _{\text{s}}\otimes \rho _{\text{h}}\otimes \rho _{\text{c}}~.$

Under dessa förhållanden blir de dynamiska rörelseekvationerna: ${\frac {d}{dt}}\rho _{\text{s}}={L}\rho _ {\text{s}}~,$ där ${L}$ är Liouville-superoperatorn som beskrivs i termer av systemets Hilbert-utrymme, där reservoarerna beskrivs implicit. Inom formalismen av det öppna kvantsystemet $L$ ta formen av Gorini-Kossakowski-Sudarshan-Lindblad (GKS-L) Markovian generator eller även känd som Lindblads ekvation . Teorier bortom den svaga kopplingsregimen har föreslagits.

Kvantabsorptionskylskåpet _

Absorptionskylskåpet är av unik betydelse för att ställa in en autonom kvantenhet . En sådan enhet kräver ingen extern ström och fungerar utan extern inblandning i schemaläggningen av operationerna. Den grundläggande konstruktionen inkluderar tre bad; ett kraftbad, ett varmt bad och ett kallt bad. Trehjulingsmodellen är mallen för absorptionskylskåpet.

Quantum trehjuling absorptionskylskåp. Enheten är sammansatt av tre bad där $T_{\text{d}}\geq T_{\text{h}}\geq T_{\text{c}}$ . Värme strömmar från kraftbehållaren och kallbadet till det varma badet.

Trehjulingsmotorn har en generisk struktur. Grundmodellen består av tre termiska bad: Ett varmt bad med temperatur $T_{\text{h}}$ , ett kallbad med temperatur $T_{\text{c}}$ och en arbetsbad med temperatur $T_{\text{d}}$ .

Varje bad är anslutet till motorn via ett frekvensfilter som kan modelleras av tre oscillatorer:

$H_{0}=\hbar \omega _{\text{h}}a^{\dolk }a+ \hbar \omega _{\text{c}}b^{\dolk }b+\hbar \omega _{\text{d}}c^{\dolk }c~~,$

där $\omega _{\text{h}}$ , $\omega _{\text{c}}$ och $\omega _{\text{d}}$ är filterfrekvenserna på resonans $\omega _{\text{d}}=\omega _{\text{h}}-\omega _{\text{c}}$ .

Enheten fungerar som ett kylskåp genom att ta bort en excitation från kallbadet såväl som från arbetsbadet och generera en excitation i det varma badet. Termen $a^{\dolk }bc$ i Hamiltonian är icke-linjär och avgörande för en motor eller ett kylskåp.

$H_{I}=\hbar \epsilon \left(ab^{\dolk }c^{\dolk }+a^{\ dolk }bc\right)~~,$

där $\epsilon$ är kopplingsstyrkan.

Termodynamikens första lag representerar energibalansen för värmeströmmar som kommer från de tre baden och kollimerar på systemet:

${\frac {dE_{\text{s}}}{dt}}={J}_{\text{h}}+{J}_{\text{c}}+{J}_{ \text{d}}~~.$

Vid stationärt tillstånd ackumuleras ingen värme i trehjulingen, alltså ${\frac {dE_{\text{s}}}{dt}}=0$ . Dessutom, i stationärt tillstånd genereras entropin endast i baden, vilket leder till termodynamikens andra lag :

${\frac {d}{dt}}\Delta {S}_{\text{u}}~=~-{\frac {{J}_{\text{h}}}{T_{\ text{h}}}}-{\frac {{J}_{\text{c}}}{T_{\text{c}}}}-{\frac {{J}_{\text{d} }}{T_{\text{d}}}}~\geq ~0~~.$

Denna version av den andra lagen är en generalisering av uttalandet av Clausius teorem ; värme flödar inte spontant från kalla till varma kroppar. När temperaturen $T_{\text{d}}\rightarrow \infty$ genereras ingen entropi i kraftbadet. En energiström utan åtföljande entropiproduktion är ekvivalent med att generera ren effekt: ${\displaystyle {P}={J}_{\text{d}}} ,$ där ${P}$ är uteffekt.

Kvantkylskåp och termodynamikens tredje lag

Det finns till synes två oberoende formuleringar av termodynamikens tredje lag som båda ursprungligen angavs av Walther Nernst . Den första formuleringen är känd som Nernst heat theorem och kan formuleras som:

• Entropin för varje ren substans i termodynamisk jämvikt närmar sig noll när temperaturen närmar sig noll.

Den andra formuleringen är dynamisk, känd som ouppnåelighetsprincipen :

• Det är omöjligt med vilket förfarande som helst, oavsett hur idealiserat det är, att reducera någon sammansättning till absolut nolltemperatur i ett begränsat antal operationer.

Vid steady state innebär termodynamikens andra lag att den totala entropiproduktionen är icke-negativ. När kallbadet närmar sig den absoluta nolltemperaturen är det nödvändigt att eliminera entropiproduktionsdivergensen på den kalla sidan när ${\displaystyle T_{\text{c}}\rightarrow 0} ,$ därför

${\dot {S}}_{\text{c}}\propto -T_{\text{c}}^{\alpha }~~~,~~~~\alpha \geq 0~~.$

För $\alpha =0$ beror uppfyllelsen av den andra lagen på entropiproduktionen i de andra baden, vilket bör kompensera för den negativa entropiproduktionen i det kalla badet. Den första formuleringen av den tredje lagen modifierar denna begränsning. Istället för $\alpha \geq 0$ inför den tredje lagen ${\displaystyle \alpha >0} ,$ vilket garanterar att entropiproduktionen vid det kalla badet är noll vid absoluta noll: ${\dot {S}}_{\text{c}}=0$ . Detta krav leder till skalförhållandet för värmeströmmen ${J}_{\text{c}}\propto T_{\text{c}}^{\alpha +1}$ .

Den andra formuleringen, känd som ouppnåelighetsprincipen kan omformuleras som;

• Inget kylskåp kan kyla ett system till absolut nolltemperatur vid begränsad tid.

Dynamiken i kylprocessen styrs av ekvationen

${J}_{\text{c}}(T_{\text{c}}(t))=-c_{V}(T_{\text{c}}(t)){\frac { dT_{\text{c}}(t)}{dt}}~~.$

där $c_{V}(T_{\text{c}})$ är badets värmekapacitet. Tar ${J}_{\text{c}}\propto T_{\text{c}}^{\alpha +1}$ och ${\ displaystyle c_{V}\sim T_{\text{c}}^{\eta }}$ med ${\eta }\geq 0$ , kan vi kvantifiera denna formulering genom att utvärdera den karakteristiska exponenten $\zeta$ av kylningsprocessen,

${\frac {dT_{\text{c}}(t)}{dt}}\propto -T_{\text{c}}^{\zeta },~~~~~T_{\text{c}}\högerpil 0,~~~~~{\zeta =\alpha -\eta +1}$

Denna ekvation introducerar relationen mellan de karakteristiska exponenterna $\zeta$ och $\alpha$ . När $\zeta <0$ kyls badet till noll temperatur på en begränsad tid, vilket innebär ett brott mot den tredje lagen. Det är uppenbart från den sista ekvationen att ouppnåelighetsprincipen är mer restriktiv än Nernst värmesatsen .

Vidare läsning

Deffner, Sebastian och Campbell, Steve. "Quantum Thermodynamics: An introduction to the thermodynamics of quantum information", (Morgan & Claypool Publishers, 2019).

F. Binder, LA Correa, C. Gogolin, J. Anders, G. Adesso (red.) "Thermodynamics in the Quantum Regime. Fundamental Aspects and New Directions." (Springer 2018)

Gemmer, Jochen, M. Michel och Günter Mahler. "Kvanttermodynamik. Uppkomsten av termodynamiskt beteende inom sammansatta kvantsystem. 2." (2009).

Petruccione, Francesco och Heinz-Peter Breuer. Teorin om öppna kvantsystem. Oxford University Press, 2002.

externa länkar

• "Nanoskala värmemotor överskrider standardeffektivitetsgränsen" . phys.org .